Моделирование тенденции временного ряда

Выявление и статистическая оценка основной тенденции развития любого экономического процесса и отклонений от него является важнейшей задачей при исследовании экономических временных рядов.

Эконометрической моделью называется регрессионная зависимость между экономическими показателями, характеризующими состояние и динамику функционирования экономических процессов и систем.

Примером эконометрических моделей являются модели временных рядов. Модели временных рядов строятся на основе исходных данных, характеризующих один объект за ряд последовательных периодов времени.

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда [1].

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:

Линейная - У(О ⁼ ^0 + ^;

Полиномиальная - У(О ⁼ ^0 + ^ + ^2^ + ... + ^_и^ ;

Экспоненциальная -      — ^е ;

Степенная –           [1].

Степенная, полиномиальная и экспоненциальная функции являются нелинейными относительно переменных, но линейными относительно параметров модели. С помощью различных преобразований эти функции можно привести к линейному виду относительно параметров. Оценивание параметров в таких функциях не представляет трудностей [3].

Существуют функции, которые являются нелинейными и относительно переменных, и относительно параметров. Примером является функция Гомперца, которая используется в демографических расчетах и в страховом деле: .

Такие функции можно назвать существенно нелинейными [3].

В данной статье на конкретном примере временного ряда в качестве уравнения тренда предлагается существенно нелинейная функция и рассматривается метод оценки ее параметров.

Рассмотрим пример.

Имеются данные о производительности труда в сопоставимых ценах 2007 года (таблица 1) [4]. Выберем уравнение тренда и определим его параметры.

Таблица 1 – Производительность труда в сопоставимых ценах 2007 года.

Годы	2000	2001	2002	2003	2004	2005	2006	2007
Производительность труда, тыс. руб.	284,3	289,5	296,3	312,3	353,0	365,7	380,3	397,5

Обозначим годы цифрами 1, 2, 3, 4, 5, 6, 7, 8.

Таблица с измененными данными имеет вид (таблица 2):

Таблица 2 – Данные для построения тренда

i	1	2	3	4	5	6	7	8
t	1	2	3	4	5	6	7	8
У i	284,3	289,5	296,3	312,3	353,0	365,7	380,3	397,5

Построим график данного временного ряда.

50 0

Годы

Рисунок 1 – Динамика производительности труда в сопоставимых ценах 2007 года, тыс. руб.

На рисунке 1 видно наличие возрастающей тенденции.

Определим оптимальное уравнение тренда.

Исходя из графика данного временного ряда можно предложить следующее уравнение тренда:

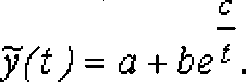
Данная функция является существенно нелинейной, так как с помощью различных преобразований ее нельзя привести к линейному виду. В этом случае можно применить метод разделимых наименьших квадратов.

Рассмотрим следующую задачу оптимизации:

8       -

^(а + Ье^ -уг)^ ->тш.

Z = 1

Найдем оценки параметров a, b, c приближенно с точностью до 0,1. Исходя из графика данного временного ряда, значение параметра c изменяется в пределах от -10 до -8.

Разобьем отрезок         на 20 частей точками сi:

с^ = -10 + ОД - ^ / = ОД,. ..ДО.

Применим метод разделимых наименьших квадратов [2].

Алгоритм метода разделимых наименьших квадратов заключается в следующем:

Для точек разбиения сj               находим значения параметров a и b,

q(a,b) = ^(a-Vbe ^ ”^2

для которых значение функции                            является наимень шим. Для этого функцию               приводим к линейному виду с помощью

c± ввода новой переменной        и применяем метод наименьших квадратов. Минимальное значение функции        зависит от значения параметра c, поэтому можно ввести функцию g(c), значения которой равны:

.

Находим значение параметра c для которого значение функции является наименьшим. По найденному значению параметра c, определяем значения параметров a и b.

Так как значения параметров a и b зависят от значения параметра c, то в результате применения метода разделимых наименьших квадратов получаем задачу одномерной оптимизации. В этой задаче единственной неизвестной переменной является параметр c. Для решения задачи одномерной оптимизации был использован метод перебора. Можно использовать и другие методы одномерной оптимизации, не требующие вычисления производных, например метод золотого сечения.

В результате использования метода разделимых наименьших квадратов приближенно с точностью до 0,1 оптимальное значение параметра c равно -9,0.

Значения параметров a и b с точностью до 0,1следующие:

a rj 282,9;& » 359,5.

Уравнение тренда имеет следующий вид:

_ 9,0

У = 282^ + 359^5 Т.

Для данного уравнения тренда значение коэффициента детерминации приближенно равно 0,98. Средняя ошибка аппроксимации приближенно равна 1,3%. Вычисленные параметры тренда показывают высокий уровень аппроксимации исходных данных. В таблице 3 приведены значения коэффициентов детерминации для различных уравнений тренда.

Таблица 3 – Значение коэффициента детерминации для различных уравнений тренда

Тип тренда	Значение коэффициента детерминации
Линейный	0,96
Степенной	0,76
Экспоненциальный	0,95
Логарифмический	0,82
Параболический (                  )	0,95

Исходя из данных таблицы, выбранное уравнение тренда является наилучшим.

Уравнение тренда для временного ряда производительности труда для Вологодской области имеет следующий вид:

7 = 282^ + 359^5 f.