Моделирование теплопереноса при локальной конвекции на фоне вертикального течения в двухслойной системе «воздух - тепловыделяющая пористая среда»

перепад температуры, и числа Дарси. Сделан вывод, что усиление тепломассопереноса за счет конвекции воздуха должно быть учтено при моделировании аккумулирующих тепло ограждающих конструкций зданий. Другое приложение задачи о тепломассобмене рассмотрено в [2], где исследовалась тепловая конвекция в прямоугольной полости с водой и тепловыделяющей пористой средой при наличии комбинированных граничных условий. Задача актуальна в применении к пассивному охлаждению бассейна мокрого хранения отработанного ядерного топлива. Показано, что увеличение внутреннего числа Релея, которое пропорционально объемной мощности тепловыделения топливных элементов, вместе с уменьшением аспектного отношения существенно снижает максимальную температуру в полости.

В области сельского хозяйства важной задачей является поддержание оптимального режима хранения продукции и своевременный отвод тепла от ее перегретых участков [3, 4]. Насыпь сельскохозяйственного сырья (например, корнеплодов, зерна, сена и другого) представляет собой пористую среду, способную выделять тепло за счет биологической активности. Управление естественной конвективной вентиляцией воздуха в этой среде в условиях внутреннего тепловыделения может достигаться разными способами: добавлением прослоек воздуха, созданием принудительного сквозного течения, внешней температурной коррекцией.

Представляемое исследование посвящено задаче тепломассобмена при конвекции, возникающей на фоне вынужденного вертикального сквозного (далее — основного) течения в двухслойной воздушно-пористой системе в поле силы тяжести. Пористая среда выделяет тепло с постоянной мощностью, пропорциональной объемной доле твердой фазы. Внешние твердые проницаемые границы системы имеют одинаковую температуру, такую, что конвективное движение возбуждается за счет внутреннего тепловыделения. Внутренняя или так называемая «проникающая» конвекция [5, 6] в тепловыделяющем пористом слое при наличии вертикального течения, насколько известно авторам, впервые изучалась в работе [7]. Зафиксировано повышение порога зарождения валиковой конвекции на фоне восходящего вертикального течения с ростом числа Пекле от 0 до 5. Влияние неоднородности фильтрационных свойств пористой среды на конвективную устойчивость сквозного течения анализировалось в [8, 9], где рассмотрены два сопряженных пористых слоя разной проницаемости, теплопроводности и мощности внутреннего тепловыделения. Обнаружена дестабилизация нисходящего сквозного течения в диапазоне чисел Пекле от –1 до 1 и стабилизация в случае смены направления этого течения на противоположное. Оба эффекта получены также в слое жидкости, частично заполненном пористой средой при наличии внутреннего тепловыделения [10, 11]. В современных исследованиях [12, 13] задача усложняется, например, учетом переменного поля силы тяжести. Уделяется внимание крупномасштабной валиковой конвекции с небольшим волновым числом.

В отличие от внутренней конвекции, вызываемой источниками тепла, находящимися внутри системы, внешняя конвекция формируется при наличии перепада температуры на границах этой системы. Ряд работ [14–16] посвящен такого рода конвекции на фоне вынужденного вертикального течения в неоднородно нагретом слое жидкости [14, 15] или в двухслойной системе [16], состоящей из сопряженных слоев жидкости и насыщенной пористой среды. Обнаружена стабилизация основного течения обоих направлений с ростом числа Пекле, а также асимметрия конвективных структур при малых значениях надкритичности и больших числах Пекле. В [16] изучалась не только крупномасштабная конвекция, охватывающая всю систему, но и локальная конвекция, которая возникает преимущественно в пределах слоя жидкости и слабо проникает в пористую среду. Смена двух возможных режимов конвекции — локального и крупномасштабного — при изменении в содержащей пористую среду системе ее параметров (отношения толщин жидкого и пористого подслоев, числа Дарси, отношения теплопроводностей подслоев и другого) впервые анализировалась в [17] в слое жидкости, частично заполненном пористой средой, и в [18, 19] в слое жидкости, ограниченном сверху и снизу двумя пористыми слоями при наличии внешнего перепада температуры. Изучению двух описанных конвективных режимов в разного рода слоистых жидкостно-пористых конфигурациях без внутренних источников тепловыделения посвящены, например, некоторые современные статьи [20–22].

Похожие локальные и крупномасштабные (в зависимости от параметров двухслойной воздушнопористой или жидкостно-пористой системы) конвективные структуры могут также наблюдаться при наличии внутренних источников или стоков тепла [5, 23, 24]. В [24] проводился линейный анализ устойчивости вертикального сквозного течения в слое воздуха, частично заполненном тепловыделяющей пористой средой. Получены значения критического порогового внутреннего числа Релея–Дарси и волнового числа, соответствующих наиболее опасным конвективным валам в широком диапазоне значений числа Пекле, отношения толщин подслоев и объемной доли твердой фазы. Обнаружена сильная дестабилизация основного течения с ростом объемной доли твердой фазы и относительной толщины воздушного подслоя, не зависящая от направления этого течения. Исследование, которому посвящена настоящая статья, является продолжением исследований [24]. Решается нелинейная конвективная задача в полной постановке и анализируется тепломассоперенос при локальном конвективном режиме с изменением надкритичности.

Структура статьи следующая. Во втором разделе статьи рассматривается постановка задачи и теоретическая модель. Конвективное движение воздуха описывается уравнениями в приближении Буссинеска, которое широко используется для моделирования слабых течений неоднородной по концентрации или температуре несжимаемой среды [см., например, 6, 15, 21, 25]. Критерии применимости приближения Буссинеска и иерархия моделей тепловой конвекции вязкого идеального газа при слабой сжимаемости изучались в [26, 27]. Согласно [26], это приближение работает при малых числах Маха M = ^еgеT < 0,03 , когда у0еg pTT < 0,1 и еt < 0,1, где еt = АT/T0 — степень неизотермичности течения (T0, AT — характерные значения температуры и ее перепада в системе) и еg = gHДу0RT/ц) — параметр гидростатической сжимаемости (H — характерный вертикальный размер системы, у0 — показатель адиабаты, R — универсальная газовая постоянная и ц — молярная масса газа). Фильтрация воздуха в пористой среде описывается моделью Дарси [28–30], подтвержденной экспериментами с газом [31] и жидкостью [32, 33]. Эта модель применима при значениях числа Дарси (или отношения проницаемости к квадрату характерной толщины системы), меньших 10–3 [6, 31, 34]. Деформация пористой среды при наличии слабого сквозного течения не принимается во внимание. В третьем разделе кратко представляются результаты решения в рамках линейной теории устойчивости конвективной задачи для основного течения и определяется число Нуссельта. Далее описывается метод численного моделирования нелинейной конвективной задачи (см. раздел 4) и обсуждаются полученные результаты (в разделе 5 анализируется вклад локальной конвекции в общий тепломассоперенос при вертикальном сквозном течении различного направления и интенсивности). В конце статьи приводятся главные выводы из выполненного исследования.

• 2.    Постановка задачи

Изучается задача конвективного тепломассопереноса в системе, образованной двумя горизонтальными подслоями и ограниченной сверху и снизу твердыми проницаемыми плоскостями, на которых поддерживается одинаковая температура T0 . На систему воздействует поле силы тяжести c ускорением свободного падения g (Рис. 1). Нижний подслой толщиной hp заполнен тепловыделяющей пористой средой, насыщенной воздухом. Верхний подслой содержит только воздух и имеет толщину ha . Система находится в условиях плоскопараллельного вертикального сквозного течения, при котором через нижнюю проницаемую границу однородно закачивается воздух отсасывается с такой же скоростью.

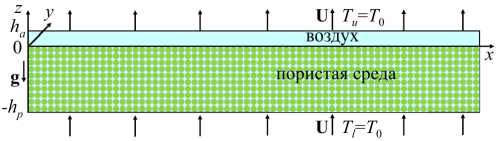
Рис. 1. Двухслойная система с тепловыделяющей пористой средой при наличии вертикального сквозного течения

со скоростью U , а через верхнюю границу —

Рассмотрение проводится на примере однородной гранулированной пористой среды с объемной долей твердой фазы ф = 0,6 и проницаемостью K = D p ( 1 - ф ) 3 Д180ф² ) , где средний диаметр гранулы D_p = 0,1 h_p [6, 35]. В силу однородности среды ее теплопроводность æ _p и объемную

теплоемкость ( р С ) можно записать в виде линейных комбинаций плотностей р и удельных теплоемкостей

C газовой (индекс a ) и твердой (индекс s ) фаз :

^Ж p = ( 1 ^- ф ) Ж a + фЖ . ,

⁽ Р ^С ) p =^{( 1} - Ф ⁾⁽ Р ^С ) а ⁺ Ф ⁽ Р ^С ) . .

В объеме пористой среды происходит тепловыделение с постоянной мощностью Q = Q s ф, пропорциональной объемной доле твердой фазы φ , где Q_s — мощность тепловыделения только твердой фазы. В качестве тепловыделяющей выбрана биологически активная среда, например, корнеплоды, зерно и другое. Для содержащих в своем составе воду и воздух твердых элементов, из которых состоят подобные среды, характерны отношения теплопроводностей ж . /ж a = 16 и объемных теплоемкостей ( Р ^С ) , /( Р ^С ) . = ³'¹⁰ 3 ЕЗ].

Как отмечалось выше, на границах двухслойной воздушно-пористой системы задается одинаковая температура, поэтому конвекция может возникнуть только за счет внутреннего тепловыделения, способного создать критический перепад температуры в воздушном и пористом подслоях. Конвективное движение воздуха, по аналогии с движением жидкости, описывается уравнениями конвекции в приближении Буссинеска [6, 15]. В пористом подслое применяется модель Дарси, что для рассматриваемой среды оправдано, поскольку ее число Дарси меньше 10-3: Da = K/hp ~ 10-5 [6, 31, 34]. Уравнения конвекции в размерных величинах представлены в статье [24], где после введения малых возмущений проведен линейный анализ устойчивости вертикального сквозного течения. В настоящей работе уравнения приводятся к безразмерному виду, и решается нелинейная конвективная задача в полной постановке в декартовых координатах, при этом координата z направлена вертикально вверх, x — горизонтально, y — перпендикулярно плоскости ( xz ).

Итак, имеют место следующие уравнения:

– в подслое воздуха

^D a f ^д v ax + b f v ⁸ v ax + v ⁸v ax )) Pr _p ( д t     (     д X      az д Z J J

д p

-    + DaA vax, дx

Da f д v^    f

— —— + b v

Pr _p V д t      V '

ax

д v az дx

az

д v az дz JJ

д p  „

" ₊ Da A v az + R 1 9. , д z

dv dv

—^ + —^ = 0 , д x    д z

– в подслое пористой среды

ж д9 a b д t

^{+ Ж} v ax

д9 a д x

v ' La9 ;

az ^1 a дz J

д p„ 0 = — -^p д x

—

v , px

0       '■'

д z

—

v pz + ^R 1 ⁹

pz

p ,

д v д v

—px_ ₊ — pz_ = o, д x    д z

д9 д9 д9

—p + v —p + v —p = A9 + 2ф.

д t     ^px д x     ^pz д z       ^p

При обезразмеривании в качестве единиц выбраны: для длины — [ x , z ] = h_p , времени — [ t ] = bh p /х f , скорости — [ v_x , v z ] = X ef/hp , давления — [ p ] = p _o v x ef/ K [24]. Здесь приняты обозначения: X eff = ж _p /( p ₀ C ) a — эффективная температуропроводность пористой среды, где р ₀ — плотность воздуха при температуре T₀; v — кинематическая вязкость воздуха; р = р₀ [ 1 — р ( T — Т₀ ) ] — плотность воздуха, где р — коэффициент объемного расширения; b = ( р₀ C )_р/( р₀ C )„ — отношение объемных теплоемкостей пористого и воздушного подслоев; ж = ж _p /ж a — отношение теплопроводностей подслоев; 9 = ( Т — Т ₀ )Д Q s h p 1(2 2ж _p ) J — безразмерное отклонение температуры от заданного значения на внешних границах. Индекс a применяется для обозначения переменных и постоянных величин в воздушном подслое, индекс p — для обозначения величин в пористом подслое.

На верхней и нижней границах двухслойной системы выполняются условия равенства нулю отклонения температуры воздуха от температуры на ограничивающих плоскостях. На этих границах нормальные компоненты скорости воздуха v _az и фильтрационной скорости v _pz равны скорости внешнего потока. На границе раздела подслоев ставятся условия непрерывности нормальных компонент скоростей, нормальных напряжений, температуры и тепловых потоков. В силу малого значения числа Дарси Da = К]h p « 10 ^—5 предполагается, что на этой границе равна нулю касательная компонента скорости воздуха [19]:

z = d :     9a = 0,   vaz = Pe, vax = 0, z = —1:

⁹ p = 0,    v pz = Pe,

z = 0 ^:    v az = v pz ,    v ax = 0,

—

Da     д v^

— b v az^x " ^{+ D} a д z

Pr p

д 2v ax дz1

^{— v} px

9 a =9 p ,

^д9 a _ _$⁸A_ ^c .

д z

д z

Далее, с целью исключения  давления,

условие

непрерывности нормальных напряжений

дv                           _

—pa + 2Da —az- = — p стандартным образом [6, 19, 24] с использованием уравнений (3) и (7) приводится дz

Da , дv

—v px

.

к виду:--bv —ax- + Da

Pr _p    ^az д z         д z^г

В задаче (3)-(11) также присутствуют безразмерные параметры: Da = K[hp, — число Дарси; Pe = Uh p /% f — число Пекле; Pr _p = b v/% f — число Прандтля для пористой среды; d = h a/ h p — отношение толщин подслоев; R I = ( g в Q s Kh p )Д 2vж _p % eff ) — внутреннее число Релея-Дарси, нормированное на ф ; Ra I = фR I — внутреннее число Релея-Дарси [6].

Для удобства решения краевой задачи (3)–(11) вводятся функции тока ψ _a , ψ _p , связанные со скоростью соотношениями:

-у v = Pe + -la., v az                    , ax

- x

5w           di

-l a , v_pz = Pe + -Zp , v

-z     pz         -x

px

—

^ p

-z ’

С учетом (12) краевая задача принимает вид:

Da ^f - X - l - f   - l 1 - 1)

--I — + b I--—— + I Pe + —— I— I I — Da A

Pr _p I- 1 V - z - x V - x )- z ))

A l a + R I^" = 0 , - x

ж - f - i - f _   - v_a 1-1 .

--+ ж I--— — + I Pe + —— I— I —A b -1    V -z -x V     -x ) -z)

—Al p + R I = 0,

- x

-  ^- l p -

—

- 1   - z - x

Pe . ')A — a

- x ) - z

z = 0:

9 a = 0,

9 p — 2ф = 0,

^z = d :     ⁹ a = 0, l a = 0,    ^{- l} a = 0,

-z z = —1:   9p = 0, vp = 0,

^- ! .

V a   V ^p ,     - z      ,

s -8    ^-9 . - _$f9 p

⁹ a =⁹ p ,     - z " ^$ - z '

-Di b I Pe + ^- l . 1

Pr _p V     - x )

^{- 2} У a

— Da

- ³l a = ^- l p

- z³      - z

• 3.    Основное течение и его устойчивость относительно малых возмущений

Основное течение представляет собой вертикальное плоскопараллельное течение с постоянной скоростью V a = V _p = Pe Y , где у — орт оси z [24]. Этому течению соответствуют функции тока ij/ a = xj/ _p = 0 и безразмерные отклонения температуры от ее значения на внешних границах двухслойной системы [24]:

.    2ф ( 1 — Pe — e - ^Pe )( e ^{ж Pe z} — e ^{ж Pe} d )

⁹ a =         Pe² ( e ^{ж Pe} d — e ~^Pe )

= 2ф f (P e + e _: ^P e d -1) ( ^{e P} e z-^e _: ^Pej + z + 1 1 ^p Pe V Pe ( e ^{ж Pe} d — e ~^Pe )              ^

а также число Нуссельта Nu _b . Поскольку источником тепловыделения является пористая среда, удобно Nu _b определить как отношение плотности полного теплового потока через границу раздела пористого и воздушного подслоев к плотности теплового потока за счет теплопроводности через эту же границу:

L

-9 -A

--- + жPe 9

- z          “

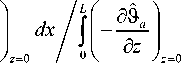
dx ,

Nu b =J где

( ^{— -}' ^ a ^- zz ) z

— плотность теплового потока за счет теплопроводности,

^{( жPe 9} a ) z

плотность

теплового потока за счет движения воздуха, L — характерный горизонтальный размер двухслойной системы. Плотности теплового потока через границу между подслоями и верхнюю границу воздушного подслоя равны между собой (—-19 a -дz + жPe9 a) =(—-9 a -zz) , так как (жPe9 a)   = 0 .

На рисунке 2 представлены вертикальные профили безразмерного отклонения температуры от ее значения на внешних границах системы и число Нуссельта, полученное при разных значениях числа Пекле.

При наличии тепловыделения постоянной объемной мощности в пределах пористого подслоя тепловые профили имеют ярко выраженные максимумы (Рис. 2 а ). В подслое максимумы соответствуют устойчивой стратификации воздуха там, где температура увеличивается с ростом координаты z (нижняя область), и неустойчивой стратификации там, где температура, наоборот, убывает с повышением z (верхняя область). При восходящем основном течении (Pe > 0) максимум теплового профиля сдвигается к границе раздела подслоев, а при нисходящем течении (Pe < 0) — к нижней границе пористого подслоя. Область неустойчивой стратификации охватывает весь воздушный подслой и при ненулевом числе Пекле тепловой профиль отклоняется от линейного (Рис. 2 а ). Это отклонение отражается на зависимости числа Нуссельта от числа Пекле, изображенной на рисунке 2 б . В отсутствие течения (Pe = 0) Nu b = 1. При восходящем течении тепловой поток через границу раздела подслоев усиливается (Nu b >  1) с ростом положительного числа Пекле, а при нисходящем течении — ослабляется (Nu b <  1) с ростом абсолютного значения отрицательного числа Пекле по сравнению с теплопередачей за счет теплопроводности при Nu b = 1.

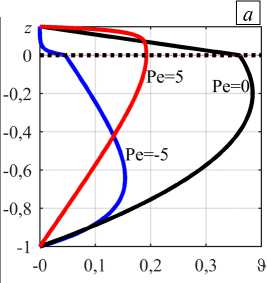
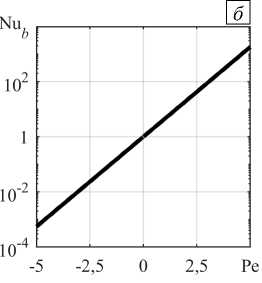
Рис. 2. Характеристики основного течения в двухслойной системе при ее относительной толщине d = 0,15 и разных значениях числа Пекле: вертикальные профили температуры ( а ), число Нуссельта как функция числа Пекле ( б )

Ранее авторами в [24] выполнено исследование основного течения на устойчивость относительно нормальных малых возмущений, периодических вдоль горизонтали с волновым числом k . В данной же работе приводятся только некоторые значения критических параметров для порога возникновения внутренней валиковой конвекции на фоне основного течения, при которых в дальнейшем будет анализироваться эволюция нелинейных конвективных режимов с ростом надкритичности. На рисунке 3 показаны графики зависимости порогового числа Релея-Дарси и критического волнового числа от числа Пекле при относительной толщине двухслойной системы, равной d = 0,15. Видно, что с ростом скорости (числа Пекле) как восходящее, так и нисходящее течения стабилизируются, то есть порог возбуждения конвекции повышается (Рис. 3 а ). При этом конвективные валы могут быть двух типов (Рис. 3 б ): при Pe < - 5,6 наиболее опасными являются крупномасштабные валы с малым волновым числом к * ® 2,4 , охватывающие всю область неустойчивой стратификации в обоих подслоях; при Pe > - 5,6 реализуются локальные валы с большим волновым числом к * (от 20 до 30), которые располагаются главным образом в верхнем — воздушном — подслое. В настоящей работе изучение ограничивается только эволюцией локальной конвекции в надкритической области параметров.

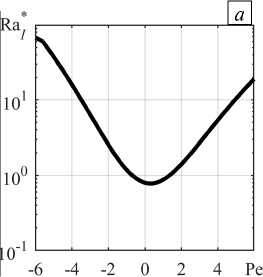
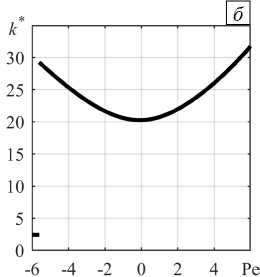
Рис. 3. Критические параметры в зависимости от числа Пекле для порога возникновения валиковой конвекции на фоне основного течения при d = 0,15 : пороговое внутреннее число Релея-Дарси ( а ), критическое волновое число валов ( б )

• 4.    Метод численного исследования стационарных режимов конвекции на фоне основного течения

Нелинейная задача в полной постановке (13)–(17) приводится к дискретному представлению в воздушном подслое (0 <  z <  d ) на прямоугольной сетке N a х M и в пористом подслое (0 <  z <  d ) и на прямоугольной сетке N p х M с помощью метода конечных разностей. В направлении оси x расчетная область ограничена размером L = 2 п nj к , где к * — критическое волновое число для наиболее опасных локальных валов, n — целое число валов. Дискретные уравнения в векторной форме имеют вид:

D ( dyjdt ) = f ( y ) ,                                            (20)

где y — вектор-столбец, элементами которого являются сеточные аналоги функций тока ψ ⁱ _a ^{, l} , ψ _p ^{j , l} и температуры 9 i, ¹ , 9^j_p ^{, 1} , определенные во внутренних узлах расчетной сетки ( x i , z l ) и ( x j , z l ) при i = 0, .., N_a , j = 0,.., N_p и 1 = 0, ..., M .

Стационарные решения y0 уравнения (20) следуют из решения системы f (У о ) = 0                                                 (21)

посредством метода Ньютона [36, 37]. Согласно методу, решения находятся в результате итераций, на которых каждое последующее приближение у 0 ^ ^{+ 1 )} приравнивается сумме предыдущего решения y j ) ) и приращения А у 0 ^г ) :

У 0 " ^{+ 1 )}= У 0 ^Г -Ал ) .                                                   (22)

Для отыскания приращения линеаризованная форма (21) представляется в виде разложения в ряд Тейлора () около y : 0

J ( У ⁽; ) ) А у 0 ^г ) =- f ( У 0 ^r ) ) ,                                            (23)

где J ( У ) = ^{d f} ( У У^ У — матрица Якоби системы (21).

Каждое полученное стационарное решение, соответствующее конвективному режиму в надкритической области параметров двухслойной системы, исследуется на устойчивость относительно малых возмущений У ~ e ^Х t , где X — их инкремент. С помощью метода Ньютона решается задача на собственные значения

{ -X D + J ( у 0 ) } У = 0,

при этом итерационный процесс осуществляются по формулам:

- D )^А У ⁽ r             r ) D + J ( У 0 ) } У ⁽ r

⁰ JU^{( r} ul      0 J

где e _c — единичный вектор-строка, в котором все элементы нулевые, кроме элемента с индексом c .

По данным численных расчетов строятся интегральные характеристики конвективных режимов в зависимости от надкритичности r = Ra I /Ra I , заданной как отношение числа Релея-Дарси при развитой конвекции (Ra _I ) к пороговому числу Релея–Дарси ( Ra^* _I ), при котором происходит потеря устойчивости основного вертикального течения. Для верификации численной схемы значение числа Ra^* _I определялось двумя разными методами: методом Ньютона (как точка надкритической вилочной бифуркации при решении нелинейной задачи (13)–(17) в полной постановке) и методом построения фундаментальной системы векторов-решений (методом ПФС) [38] из решения линейной задачи устойчивости основного течения [24]. Рассчитанные критические параметры при d = 0,15 , ф = 0,6 и разных значениях числа Пекле приведены в таблице. Сетка имела размер ( N_a + N_p ) х M , где N_a + N_p = 200 , а M задавалось таким, чтобы в воздушном слое форма ячеек была как можно ближе к квадратной. Отклонение результатов, полученных разными методами, составляет не более 1%. В статье [24] показано, что данные, вычисленные в рамках линейной теории устойчивости, хорошо согласуются с результатами предшествующих работ [8, 28, 34], где рассматривался предельный случай тепловыделяющего пористого слоя ( d = 0).

Таблица. Критические параметры для порога конвекции при d = 0,15 , ф = 0,6, найденные из решения нелинейной задачи тепловой конвекции в полной постановке методом Ньютона и линейной задачи устойчивости методом ПФС

Pe	Метод Ньютона		Метод ПФС		Отличие, %
	Ra |	к'	Ra |	к'	Ra |	к'
–5	37,869	27,795	37,546	27,701	0,85	0,34
–3	6,4227	23,315	6,4049	23,293	0,28	0,094
–2	2,5725	21,673	2,5680	21,662	0,17	0,051
0	0,79708	20,271	0,79618	20,269	0,11	0,0099
2	1,4101	21,971	1,4082	21,971	0,13	0
3	2,6948	23,768	2,6914	23,770	0,13	0,0084
5	10,369	28,688	10,333	28,691	0,35	0,010

• 5.    Численные результаты

Приведем некоторые наиболее важные численные результаты, полученные при решении нелинейной задачи (13)–(17) методом Ньютона. Ограничимся обсуждением стационарных режимов локальной конвекции, возникающей на фоне вертикального основного течения при d = 0,15 , ф = 0,6 и Pe <- 5,6 (Рис. 3), и ее влияния на теплоперенос в двухслойной системе. Определим абсолютное отклонение числа Нуссельта Nu , характерного для этой конвекции от числа Нуссельта Nu _b при основном течении (см. формулу (19)). Число Nu , по аналогии с числом Nu _b , записывается как отношение плотности полного теплового потока при конвективном течении к плотности теплового потока через границу между пористым и воздушным подслоями за счет теплопроводности:

L

' +     .■ dz            11

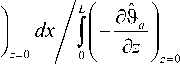
dx ,

Nu = JI о V где (-53а /dz)

— плотность теплового потока за счет теплопроводности при основном течении,

(^- 59 a / дz + $Pe 9 a ) _z = o = (^- 59 _Q / дz ) _zzd — плотность теплового потока при вторичном течении.

Сначала рассмотрим наиболее простой случай, когда конвекция возбуждается вследствие потери устойчивости механического равновесия воздуха в отсутствие вынужденного основного течения при Pe = 0 и Nu b = 1. На рисунке 4 а приведено абсолютное отклонение числа Нуссельта ( Nu - Nu b ) в зависимости от надкритичности r = Ra I /Ra I * , где Ra I — число Релея-Дарси при развитой конвекции, Ra I * — критическое число Релея–Дарси, при котором конвективное движение только появляется. Видно, что в точке потери устойчивости механического равновесия (см. точку B на Рис. 4 а ) образуется ветвь, по которой прослеживается, что с увеличением r растет и отклонение ( Nu - Nu b ) , то есть потеря устойчивости равновесия сопровождается надкритической вилочной бифуркацией. На рисунке 4 б показаны зависимости действительной части инкремента X от надкритичности. Устойчивые режимы наблюдаются при X < 0 . К ним относятся, соответственно, механическое равновесие при r <  1 (пунктирная линия) и стационарная конвекция при r >  1 (сплошная линия).

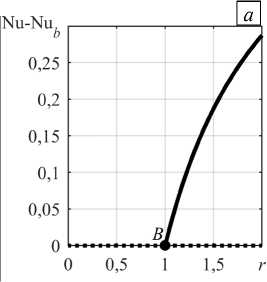
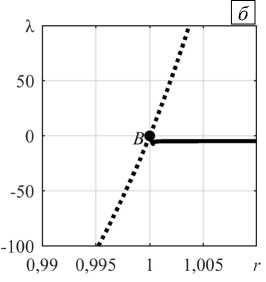
Рис. 4. Теплоперенос при локальной конвекции с изменением надкритичности в отсутствие вертикального основного течения

( Pe = 0 ): абсолютное отклонение числа Нуссельта ( а ), действительная часть инкремента возмущений ( б ); механическое равновесие воздуха (пунктирная линия), конвективное течение (сплошная линия), B – точка вилочной бифуркации

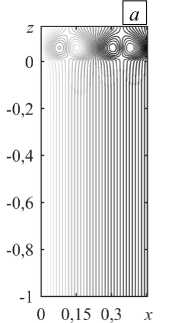
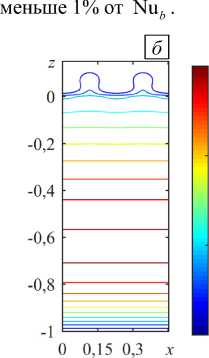
Надкритическая вилочная бифуркация проявляется в формировании устойчивых стационарных течений, представляющих собой конвективные валы, локализованные в воздушном подслое (Рис. 5). Здесь также изображены линии тока и изотермы, отвечающие эволюции стационарных режимов локальной конвекции с ростом надкритичности в отсутствие основного сквозного течения (Pe = 0). Видно, что конвективные валы возникают в небольшой зоне, ограниченной воздушным подслоем по вертикали (Рис. 5 а , в ). Изотермы здесь искажаются в соответствии с подъемно-опускным течением, что говорит об интенсификации теплообмена (Рис. 5 б, г ). Конвективное течение слабо проникает в нижний пористый подслой, в пределах которого газ практически не движется. В этой области теплопередача происходит, главным образом, за счет теплопроводности. С ростом надкритичности скорость течения возрастает, однако, проникновение возмущений в пористую среду остается слабым.

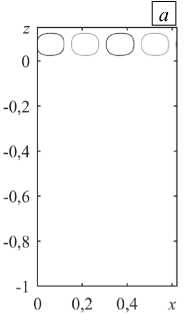
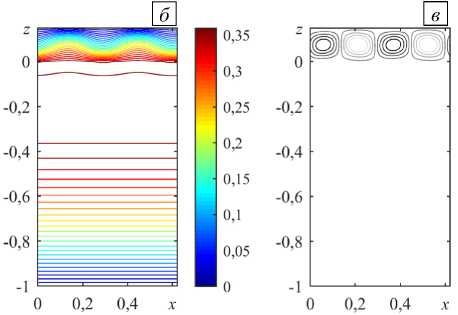
Рис. 5. Локальная конвекция при разных значениях надкритичности r в отсутствие вертикального основного течения ( Pe = 0 ); линии тока ( а ) и изолинии 3 ( б ) при r = 1,1; линии тока ( в ) и изолинии 3 ( г ) при r = 2

Теперь рассмотрим естественную конвекцию, образующуюся на фоне вертикального основного течения. На рисунке 6 показано абсолютное отклонение числа Нуссельта ( Nu - Nu b ) в зависимости от надкритичности при разных фиксированных значениях числа Пекле. Отрицательные числа Пекле (Pe <  0) соответствуют нисходящему основному течению (Рис. 6 а ), положительные (Pe > 0) — восходящему основному течению (Рис. 6 б ). Видно, что независимо от направления основного течения, естественная конвекция, в сравнении с теплопередачей за счет теплопроводности, усиливает теплообмен в системе. При всех Pe наблюдается рост отклонения ( Nu - Nu b ) с повышением надкритичности.

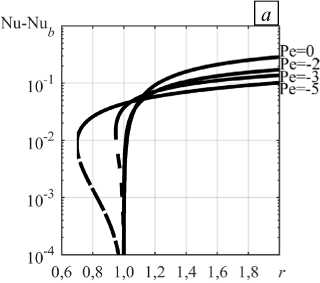
Рис. 6. Теплоперенос при локальной конвекции с изменением надкритичности на фоне вертикального основного течения

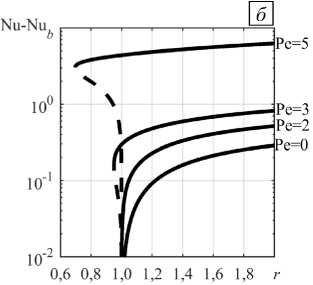
при разных значениях числа Пекле Pe : абсолютное отклонение числа Нуссельта при Pe <  0 ( а ) и Pe >  0 ( б ); неустойчивые конвективные режимы (штриховые линии), устойчивые конвективные режимы (сплошные линии )

Однако при фиксированном значении надкритичности скорость теплопереноса за счет локальной конвекции на фоне нисходящего основного течения оказывается меньше, чем на фоне восходящего основного течения. Пояснить такой результат можно с помощью рисунков 7 и 8, где изображены линии тока и изотермы для этих двух видов течений. Судя по рисунку 7, нисходящее течение противоположно потоку тепла, направленному от тепловыделяющей пористой среды к верхней границе воздушного подслоя. Оно смещает центры конвективных вихрей ближе к границе раздела подслоев и ослабляет этот поток. Восходящее течение (см. Рис. 8), наоборот, совпадает по направлению с тепловым потоком и усиливает его. Центры конвективных вихрей, возникающих на фоне этого течения, смещаются к верхней границе воздушного подслоя. Из сравнения отклонения (Nu - Nub) со значением Nub (см. Рис. 2б) следует, что при нисходящем основном течении величина отклонения начинает превышать Nub при Pe < -1. Дальнейшая интенсификация нисходящего течения делает теплоперенос Nub несущественным по сравнению с теплопереносом (Nu - Nub), возникающим в надкритической области за счет локальной конвекции. Например, в надкритической области при r = 2 и Pe =-5 теплоперенос Nub составляет только 0,5% от (Nu - Nub). В случае восходящего основного течения (Pe > 0) теплоперенос Nub значительно превышает отклонение (Nu-Nub). С ростом числа Пекле вклад локальной конвекции в теплоперенос уменьшается и с течением времени становится незначительным. Начиная со значения Pe « 3, характеризующее этот вклад отклонение (Nu - Nub),

количественно становится

0,15

о,1

0,05

о

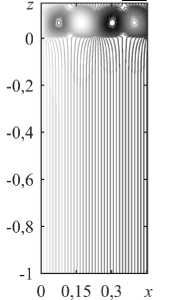
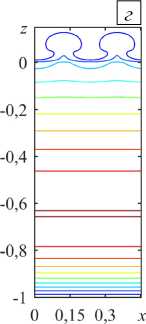
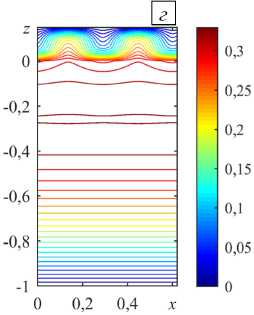
Рис. 7. Локальная конвекция при разных значениях надкритичности r на фоне нисходящего вертикального основного течения с Pe = - 5: линии тока ( а ) и изолинии 3 ( б ) при r = 0,8 ; линии тока ( в ) и изолинии 3 ( г ) при r = 2

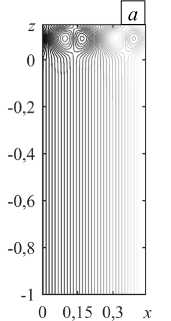
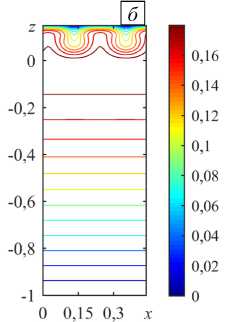
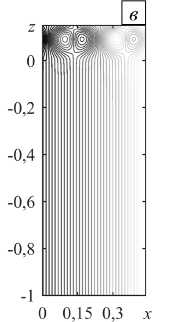
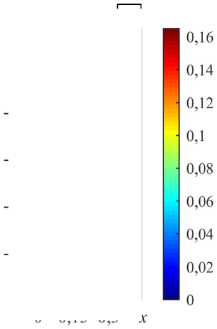
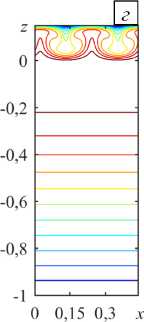
Рис. 8. Локальная конвекция при разных значениях надкритичности r на фоне восходящего вертикального основного течения с Pe = 5 : линии тока ( а ) и изолинии 3 ( б ) при r = 0,8 ; линии тока ( в ) и изолинии 3 ( г ) при r = 2

Описанная выше локальная конвекция на фоне вынужденного основного течения может возбуждаться как мягким, так и жестким образом. В первом случае потеря устойчивости этого течения относительно малых монотонных возмущений приводит к надкритической вилочной бифуркации (см. Рис. 6, сплошные линии при |Pe| <  2); стационарные режимы конвекции являются устойчивыми во всем исследованном диапазоне значений надкритичности. Иная бифуркационная картина наблюдается при достаточно больших по величине числах Пекле (|Pe| >  2): потеря устойчивости основного течения сопровождается обратной (подкритической) вилочной бифуркацией, которая порождает вторичный конвективный режим, неустойчивый по отношению к малым возмущениям (см. Рис. 6, штриховые линии при |Pe| >  2). На рисунке 9 показан пример такой бифуркации для абсолютного отклонения числа Нуссельта в зависимости от надкритичности при Pe = -5 . Рисунок 10 иллюстрирует соответствующую зависимость действительной части инкремента возмущений от надкритичности. В точке седлоузловой бифуркации S происходит рождение третичного стационарного конвективного режима (Рис. 9 б ). В некоторой окрестности от точки S до точки X этот режим неустойчив монотонным образом (Рис. 10 в ). Между точками A и X третичный режим неустойчив относительно колебательных возмущений, что указывает на возможность существования колебательного режима течения.

Правее точки X третичный конвективный режим устойчив и представляет собой совокупность конвективных валов на фоне вертикального течения, локализованных в воздушном подслое (Рис. 7).

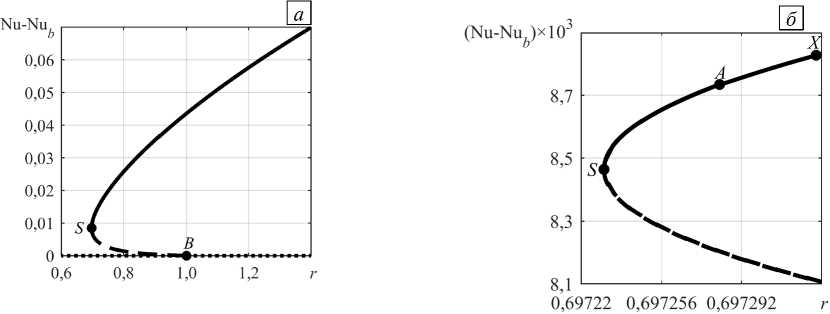
Рис. 9. Локальная конвекция на фоне нисходящего вертикального основного течения c Pe = - 5 : абсолютное отклонение числа Нуссельта в зависимости от надкритичности ( а ) и его участок в увеличенном масштабе ( б ); вторичный конвективный режим (штриховая линия), третичный конвективный режим (сплошная линия)

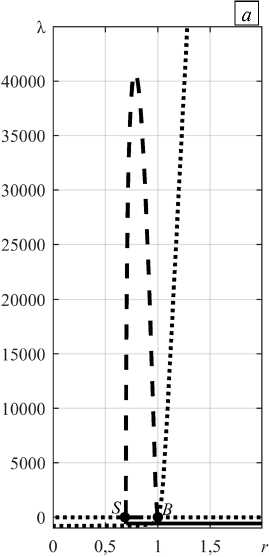
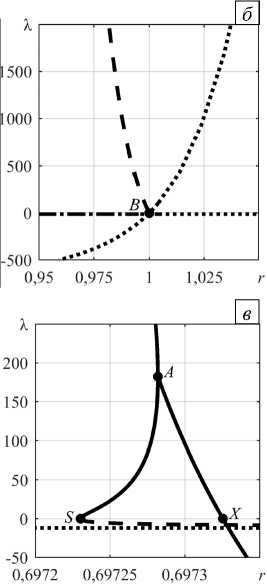
Рис. 10. Зависимость от надкритичности r действительной части инкремента возмущений для режима локальной конвекции на фоне нисходящего вертикального основного течения c Pe = — 5 ( а ) и ее увеличенные фрагменты ( б ) и ( в ); основное течение (пунктирная линия), вторичный конвективный режим (штриховая линия), третичный конвективный режим (сплошная линия)

• 6.    Выводы

Исследовано изменение теплового потока при локальной конвекции, возникающей на фоне принудительного вертикального основного течения в двухслойной системе, состоящей из подслоев воздуха и тепловыделяющей гранулированной пористой среды. Проведено численное моделирование нелинейной конвекции на основе метода Ньютона. Для описания конвекции в воздушном и пористом подслоях использовано приближение Буссинеска. Считалось, что фильтрация воздуха в пористой среде подчиняется закону Дарси.

Показано, что при одинаковом абсолютном значении скорости основного течения (числе Пекле), общий теплоперенос при нисходящем течении оказывается слабее такового при восходящем течении. Это можно объяснить тем, что в первом случае направление теплопереноса противоположно направлению основного течения, а во втором случае совпадает с ним. Локальная конвекция усиливает перенос тепла из нижнего тепловыделяющего пористого подслоя в верхний воздушный подслой как при восходящем, так и при нисходящем основном течении. Наблюдается рост числа Нуссельта с повышением надкритичности.

Несмотря на усиление теплопереноса за счет возбуждения в системе локального конвективного течения, вклад этого течения в общий теплоперенос зависит от направления и интенсивности основного течения. Результаты расчета позволили заключить, что относительный вклад локального течения в теплоперенос существенно превосходит по величине аналогичный параметр нисходящего основного течения. При восходящем основном течении вклад вторичного течения в теплоперенос становится незначительным при числах Пекле, больших 2.

При слабом основном течении (малом числе Пекле) локальная конвекция возбуждается мягко в результате прямой вилочной бифуркации. При числах Пекле, превосходящих по модулю 2, потеря устойчивости основного течения сопровождается обратной вилочной бифуркацией, порождающей вторичный стационарный конвективный режим, неустойчивый по отношению к малым возмущениям. В точке седлоузловой бифуркации возникает третичный стационарный режим, который становится устойчивым с ростом надкритичности. В некотором интервале чисел Релея–Дарси наблюдается мультистабильность, при которой вместе с основным течением возможно существование третичного конвективного режима при фиксированных значениях параметров. Последнее обстоятельство говорит о вероятности жесткого возбуждения конвекции.

Исследование выполнено за счет гранта Российского научного фонда № 21-71-10045 в Пермском государственном национальном исследовательском университете.