Моделирование теплопроводности порошковой среды применительно к задаче селективного лазерного плавления

Метод селективного лазерного спекания/плавления (СЛС/П)

Порошковый материал послойно спекается лазерным излучением (ЛИ). Для этой методики нужны мелкодисперсные термопластичные порошки с хорошей вязкостью и быстро затвердевающие, например, полимеры, воск, нейлон, керамика или металлические порошки с добавкой легкоплавкого связующего. Методика предложена впервые Карлом Декартом (Carl Deckard) в 1989 году. Способы спекания/сплавления частиц порошка при СЛС/П. Спекание частиц порошка может осуществляться различными способами: жидкофазное спекание, совмещение процесса СЛС и самораспространяющегося высокотемпературного синтеза, совмещение процесса СЛС с процессами горячего изостатического прессования, совмещение СЛС с химическими реакциями с участием газовых добавок, совмещение СЛС с процессом гелевого литья, совмещение СЛС с послойным нанесением покрытий [2].

Наиболее значимыми параметрами, определяющими качество спекаемых слоев, являются характеристики исходных материалов и параметры спекания. К характеристикам исходных материалов относятся размер и форма частиц, насыпная плотность и величина удельной поверхности порошка. Параметрами спекания являются мощность лазера, скорость сканирования, интенсив- ность лазерного излучения, частота импульсов, защитная атмосфера, время выдержки. Качество спекаемых слоев характеризуется максимально достижимой точностью, равномерной плотностью, максимальной и минимальной толщиной обрабатываемого слоя [3].

Свойства порошковой среды

При изучении механизма и кинетики процессов, происходящих в спекающемся по р истом теле, необходимо иметь в виду особенности фазового равновесия, обусловленные дисперсностью фаз. Это связано с тем, что и порошинки, из которы х спрессовано пористое тело («фа з а вещества»), и поры («фаза пустоты»), как правило, имеют такие линейные раз м еры, когд а эффекты, обусловленные искривленностью границы между со существенными фазами, могут оказаться значительными [4].

Исследования показывают, что выбор оптимальных режимов для тех н ологии СЛП требует знания теплофизических характеристик используемых порошковых матери а лов.

Моделированию распределения тепла по системе поры-частицы в зависимости от степени укладки и формы частиц, в том числе и для целей р а счета температур в зоне спекания при СЛП, посвящено несколько работ [1, 5]. При этом прямой теоретический расчет теплофизических характеристик материала при СЛП наталкивает на зна ч ительные трудности. По этой причине была разработана методика, согласно которой проводились исследования тепловых полей при лазерном воздействии (ЛВ) по глубине используемых пор о шковых композиций [6].

Экспериментальное изучение переноса тепла в пористых средах

Процесс теплопроводности – один из так называемых процессов те п ломассопереноса, играющих огромную роль в природе и в технике. В ра б оте [1] был проведен р я д экспериментов для изучения теплопроводности порошковой среды, исследования проводились на установке показанной на рис. 1. Лазерный луч 2 от технологической лазерной установки 1 (К в ант-60, λ = 1,06 мкм) с помощью отклоняющих дефлекторов 3 направлялся через штатную фокусирующую линзу 4 в зону обработки на разровненную поверхность свободно насыпанной в бо л ьшом объеме порошковой композиции 5, которая находилась на массивном металлическом основании 6 для осуществления эффективного теплоотвода из порошковой среды. Температура измерялась с помощью термопары 7, которая могла свободно перемещаться внутри порошковой среды вверх и вниз по оси Z посредством микрометрической подвижки 8.

Лазерная установка работала в непрерывном ре ж име. Проводились из м ерения те м пературы на глубине Н при различной мощности ЛВ. Были построены графики зависимости Т ( Н ), для алюминиевого порошка график имеет вид рис. 2. Анализ эксперименталь н ых результатов показывает существование в поверхностных слоях порошковых материалов значительных температур, во многих случаях сравнимых с температурой литого материала, для алюминия Т _пл = 660 °С.

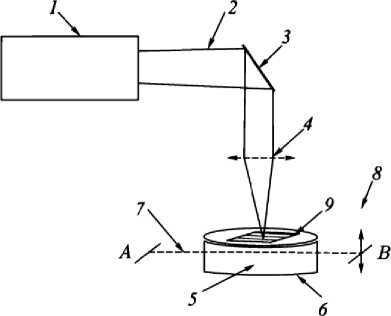
Рис. 1. Схема экспериментальной установки

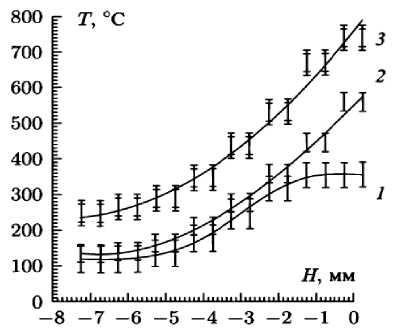
Рис. 2. Экспериментальное распределение температур Т по глубине Н от поверхности свободно насыпанного алюминиевого порошка: Р = 0,7 Вт (1);

Р = 1,6 Вт (2); Р = 2,6 Вт (3)

Была сформулирована и решена задача для расчета коэффициента теплопроводности в порошковой среде, что привело к оптимизации режимов СЛП. Зная мощность теплового источника и значения температур на разных глубинах, можно оценить некоторые теплофизические характеристики обрабатываемой лазерным излучением (ЛИ) порошковой среды [1].

Основные уравнения

Сложность постановки краевой задачи для лазерной обработки порошковых материалов связана в основном с необходимостью моделирования процесса поглощения ЛИ сильно неоднородной порошковой средой. Для квазистационарного случая (эксперимента, описанного ранее) нагрева порошковой среды неподвижным источником ЛВ в первом приближении постановка задачи может быть записана в таком виде [6]:

d²r ₊ idr ₊ d²r ₊ ил/е ex / dr²    r dr   dz²     X exp

-

r i

^{2 r} —

-

az) = 0,

-^d^zo) = ^^ - g) exp / r^\, 7(r, z ^ m) = 0, dz                          r^

где λ – коэффициент теплопроводности; І , r n – плотность мощности и радиус пятна ЛВ; А , α , θ – коэффициенты поверхностного, объемного поглощения и пористость среды.

Параметр θ отвечает за структуру тела, θ = 0 для твердого тела и θ = 1 для полностью пористого тела. Порошковые смеси характеризуются 0 < θ <  1.

С помощью интегрального преобразования Ханкеля найдено точное решение данной краевой задачи:

аЛ/Or^ m                  s2r2 Sexp(-az)-aexp(-5z) 6-i

T(r,z) =^X-Jo 7o(6r)d6exp(^-)[                    rexp(-6z)],           (3)

где J 0 – функция Бесселя нулевого порядка.

Температура в центре пятна ЛВ определяется по формуле:

аЛ/Or^ т           s2r2    е е-i

^/ '"'   ⁰      ,. - ^^V'^XP:     , :|.....j'                                      ⁽⁴⁾

В работе [1] сделан вывод, что функция Т обратно пропорциональна теплопроводности среды λ и стремится к своему асимптотическому значению при возрастании объемного поглощения α, при этом Т практически не зависит от θ. В качестве примера в логарифмическом масштабе представлена проекция 3-мерного графика зависимости функции температуры от коэффициентов теплопроводности λ и объемного поглощения α на плоскость для случая нагрева неподвижным

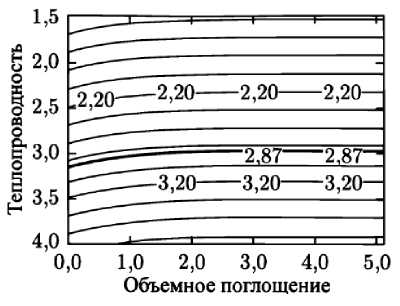
Рис. 3. Проекция на плоскость в логарифмических координатах 3-мерного графика расчетной зависимости температуры от α и λ

лазерным пучком порошка Аl, для Р = 2,6 Вт, Т = 740 °С (рис. 3).

Изотерма lg ( Т ( r , z = 0) = 740 °С) ≈ 2,87 (жирная линия) в плоскости координат Y – lg ( λ ) и X – lg ( α ) . При α > 10 2 –10 3 см –1 для Аl функция Т (lg ( λ ), lg ( α )) стремится к своему асимптотическому пределу, соответствующему максимальной температуре на поверхности порошка, при этом значение коэффициента теплопроводности практически перестает изменяться. Данная методика расчета позволяет оценить значение коэффициента теплопроводности в порошках при скоростном ЛВ. Полученные значения коэффициента теплопроводности порошков значительно отличаются от теплопроводности материалов, из которых они сделаны. В работах [7, 8]

приведены результаты экспериментальных измерений коэффициента теплопроводности, теплоемкости и глубины спекания чистых порошковых металлов и полимеров. Оказывается, у ме- таллических порошков значение теплопроводности на несколько порядков меньше соответствующих значений монолитных материалов, а для полимеров значение отличается лишь в несколько раз.

Для оценки значения коэффициента теплопроводности металлополимерных композиций (МПК) используют соотношения [9]:

^ см

7 1 X 1 +7 2 ^ 2 , 7 1 +^ 2    ;

ЛмПК = 0Ла + Лсм(1-0),

где V1, λ1, и V2, λ2 – объемные доли компонентов МПК и их теплопроводности; λа – теплопровод- ность воздуха; λмпк – теплопроводность металлополимерной композиции.

С учетом слабой тепловой проводимости воздуха в порошковых смесях [10] считается, что теплопроводность порошка λр равняется

. = (1-0)Л₅

р    ^{1 + ф}Л₅/Л а '

где X ^ - теплопроводность твердого тела, из которого сделан порошок; ф - некоторый эмпирический сомножитель.

Во всех тепловых модельных постановках по СЛП порошковых композиций у зарубежных исследователей [11–13] используется соотношение (7) или его модификации не только для опре- деления теплопроводности, но и плотности, теплоемкости, температуропроводности.

Теплопроводность порошковых материалов

В настоящее время в ряде отраслей промышленности имеются большие тепловые потоки от одной поверхности к другой, вследствие чего даже незначительные контактные сопротивления вызывают местные перегревы, что часто крайне нежелательно. В работе [14] была изучена эффективная теплопроводность зернистых систем, которая рассматривалась как функция пористости, теплопроводности газа, заполняющего поры материала, теплопроводности газового микрозазора, теплопроводности самих частиц и контактной теплопроводности на стыке частиц.

Для теоретических исследований процессов селективного лазерного спекания необходимой является разработка методов описания эффективных коэффициентов теплопроводности (ЭКТ) порошковой среды, которые учитывают, что при нагреве может происходить частичное или полное плавление материала сфер, приводящее к изменению структуры среды. Отсюда следует важное требование к моделям ЭКТ: структурная модель в пределе полного плавления материала твердых частиц должна давать значение эффективной теплопроводности, которое сшивается с эффективной теплопроводностью, даваемой бесструктурной моделью. Для случая полного плавления частиц предлагается метод расчета эффективной теплопроводности расплава с газовыми включениями, который описан в работе [15].

Результаты экспериментальных исследований теплопроводящих свойств порошковых сред в газовой атмосфере представлены зависимостями ЭКТ от давления и температуры среды, размеров частиц и их объемной доли [16–18]. Эксперименты свидетельствуют, что ЭКТ увеличивается с увеличением давления газа и стремится при высоких давлениях к насыщению.

Реализация модели

Современные вычислительные технологии и пакеты программ позволяют рассматривать достаточно подробные модели, в том числе – состоящие из большого числа взаимодействующих частиц. Но создание модели процесса селективного лазерного плавления наталкивается не только на вычислительные трудности, но и на необходимость описывать сложное поведение среды, включая теплопередачу от луча к частицам порошка, теплопередачу между частицами через области контакта и газовые зазоры малой толщины, фазовые превращения материала и т. д.

В качестве первого этапа создания модели, описывающей материал как набор отдельных взаимодействующих частиц, предлагается использование существующих пакетов, реализующих метод конечных элементов. При этом часть физических особенностей задачи не может быть напрямую смоделирована и должна быть заменена подбором «эффективных» значений параметров, обеспечивающих получение корректных результатов. Рассмотрим такой процесс на примере подбора параметров теплопроводности.

Для проверки возможности подбора параметров, описывающих теплопроводность в дискретной (состоящей из отдельных частиц) модели, было выполнено сопоставление численного решения двух задач: 1) о нагреве объема однородного материала с параметрами, определенными для порошка (рис. 4); 2) о нагреве набора шарообразных частиц, контактирующих между собой (шарообразная форма характерна для частиц, получаемых распылением расплавов) (рис. 5). Расчеты выполнялись численно с использованием пакета ANSYS (ANSYS/LS-DYNA).

Рис. 4. Расчетная модель однородного материала

Рис. 5. Расчетная модель шарообразных частиц (порошковая среда)

Нагрев производился с одной стороны по всему объему, а зависимость температуры от времени регистрировалась на противоположной стороне. Примеры зависимостей показаны на рис. 6. Из графика следует, что расплавление хромового порошка происходит при температуре 300 °С в течение 0,5 минут, в качестве параметров теплового контакта использовался контакт типа *CONTACT SURFACE TO SURFACE THERMAL. Описание теплового контакта осуществляется при помощи ряда параметров:

• •    K – теплопроводность через среду, заполняющую пространство между контактными поверхностями. Теплопередача описывается уравнением h _cona = ^—;

• •    FRAD – теплопередача за счет излучения, описывается формулой:

f rad = —+2__1'

El Е ₂

где о - постоянная Больцамана; е_г и е ₂ — степень черноты взаимодействующих тел.

Теплопередача описывается уравнением h _rad = f _rad (T _m + Т <. )(Т т + Т/);

• •    H0 – теплопередача между касающимися телами;

• •    LMIN – величина минимального зазора, для которого теплопроводность считается как для

касающихся тел;

• •    LMAX – расстояние между поверхностями, при превышении которого тепловой контакт не рассчитывается.

Тепловой контакт во 2-й задаче описывался следующим набором параметров: K , Frad , H 0 , L min , L max (теплопроводность контакта равна H 0 при зазоре L <  L min , K / L + Hrad при L min < L <  L max ).

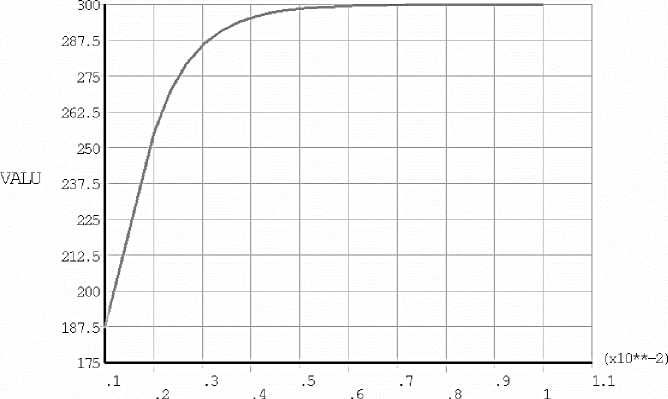
TIME

Рис. 6. Результаты (график зависимости температуры от времени)

Таким образом, изменяя глубину пористого слоя (параметр L _min), в описании контакта можно добиваться различных значений теплопередачи.

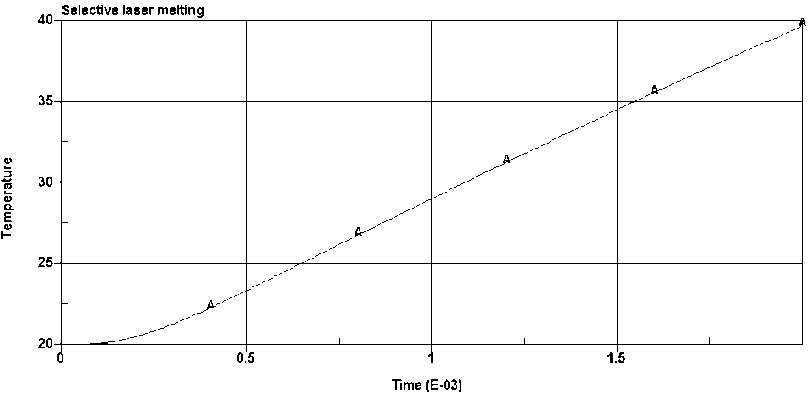
Рис. 7. Зависимость температуры в узле от времени при L min = 40 мкм

Новое поколение СЛП

Инновационные технологии стали еще одним шагом на пути к энергоэффективному производству, примером является промышленная система селективного лазерного п лавления S L M 500 HL с уникальной технологией мультилазерного луча. Система SLM 500HL может быть оснащена двумя лазерами мощностью 400 или 1000 Вт каждый или до четырех лазеров по 400 Вт. Область построения моделей – 500 × 280 × 325 см³, минимальная толщина наносимого слоя – 20 мкм.

Работа обоих лазерных лучей (400 + 1000 Вт) происходит на порошковом слое с применением блока для 3D сканирования. В SLM 500HL включен процесс для отображения об о лочкового стержня с двумя различными лазерными лучами. Работа лазерных лучей м ожет осущ е ствляться одновременно и параллельно, либо независимо, что позволяет улучшить производительность. Транспортировка металлического порошка производится с использованием конвейерной системы подачи в связи с увеличением веса и объема. Автоматизированное распределение порошка позволяет сократить время работы и освобождает от загрузки вручную из различных емкостей [19].

Заключение

Теоретическое и экспериментальное изучение процесса теплопроводн о сти порошковой среды применительно к методу селективного лазерного плавления является важной задачей.

Рассмотрены основные факторы, определяющие качество спекаемых слоев при СЛП. Выявлено, что знание о распределении температур по глубине позволяет оценить значение коэффициентов теплопроводности в этих порошковых следа х ; значение теплопроводности на несколько порядков у металлических порошков меньше соответствующих значений монолитны х материалов, для полимеров значение отличается лишь в несколько раз. Изучен экспериментальный метод по исследованию переноса тепла в пористых средах. Составлены модели, и проведены расчеты с помощью пакета ANSYS (ANSYS/LS-DYNA).