Моделирование теплового состояния бесконечно протяженного тела с учетом динамически изменяющихся граничных условий третьего рода

В настоящее время широко развита и используется теория моделирования теплового состояния тел различной формы, описывающих реальные объекты для разнообразных технологических процессов. Довольно большое количество вариантов постановки задачи теплопроводности для тел различной формы приведено в трудах А.В. Лыкова, рассматривающего решение уравнения нестационарной теплопроводности (полуограниченное тело, неограниченная пластина, сплошной цилиндр, шар, полый цилиндр) несколькими методами (разделение переменных, операционные, интегральные преобразования Фурье и Ханкеля).

Однако математическое описание теплового состояния тела для конкретных производственных условий имеет существенные отличия в определении формы исследуемого тела и граничных условий. Развитие и применение теории теплопроводности в металлургической промышленности привело к появлению нескольких научных направлений в исследовании теплового состояния тел. Основные положения этих направлений изложены в трудах В.Т. Борисова, В.В. Виноградова, В.Т. Журавлева, Я.Я. Клявиня, Д.П. Евтеева и др. Отличительными особенностями этих направлений являются применение уравнения теплопроводности для описания тепловых процессов в многослойных бесконечных телах круглого или прямоугольного сечения и задание постоянного коэффициента теплоотдачи с поверхности тела в граничных условиях третьего рода.

Постоянство в значениях коэффициента теплоотдачи не позволяет построить адекватную математическую модель теплового состояния объектов, которые нагреваются или охлаждаются в зональных агрегатах, построенных при условии перемещения объекта по технологическим зонам с изменением граничных условий. К таким технологическим процессам можно отнести нагревание заготовок в зональных методических печах, охлаждение заготовок на машинах непрерывной разливки, нанесение покрытия на металлическую полосу в агрегатах оцинкования и т.п. При конструкционной сложности агрегатов, наличии закрытого пространства и высоких температур в окружающей среде затруднительно осуществить методики динамического измерения, приведенные в работах [1 – 3]. Поэтому до настоящего времени остается актуальной проблема построения адекватной математической модели для описания теплового состояния тела при динамическом изменении граничных условий третьего рода. Далее рассмотрим процесс охлаждения заготовок на машинах непрерывной разливки стали, построенных по зональному принципу и при условии перемещения заготовки с переменной скоростью по зонам вторичного охлаждения.

1.    Математическая модель теплового состояния бесконечно протяженного прямоугольного тела

Математическая модель теплового состояния заготовки с учетом конструкционных особенностей машины непрерывного литья заготовок требует введения следующих допущений:

• •    геометрические размеры заготовки таковы, что ее металлургическая длина во много раз превышает размеры поперечного сечения, поэтому она может быть представлена как бесконечный прямой параллелепипед с размерами поперечного сечения a и b (см. рис. 1);

• •    изменение температурных полей внутри тела происходит только за счет теплопроводности;

• •    скорость перемещения зафиксированного поперечного сечения по зонам агрегата достаточна для того, чтобы вдоль металлургической длины заготовки можно было бы пренебречь теплопереносом путем теплопроводности;

• •    охлаждение тела является несимметричным (см. рис. 1);

• •    начало отсчета для системы координат располагаем в геометрическом центре поперечного сечения заготовки;

• •    скорость перемещения фиксированного сечения не является постоянно заданной величиной даже в пределах одной зоны машины непрерывного литья заготовок (см. рис. 1).

На рис. 1 введены обозначения: x , y – пространственные координаты для фиксированного сечения бесконечного тела, м; τ – временная координата, с; V – скорость движения фиксированного сечения тела, м/c; a и b – геометрические размеры фиксированного поперечного сечения тела, м; а(х, у, т ) — значение коэффициента теплоотдачи с поверхности тела, Вт/(м 2 • ° C); индексы М, Б, У - обозначение граней тела.

Вид функции а(х, у, т ) определяется конструкционными особенностями машины непрерывного литья заготовок, в частности, схемой расстановки форсунок для водовоздушного охлаждения, схемой роликового полотна и плотностью орошения поверхности водовоздушным потоком, форма которого определяется возможностями форсунки. Учитывая

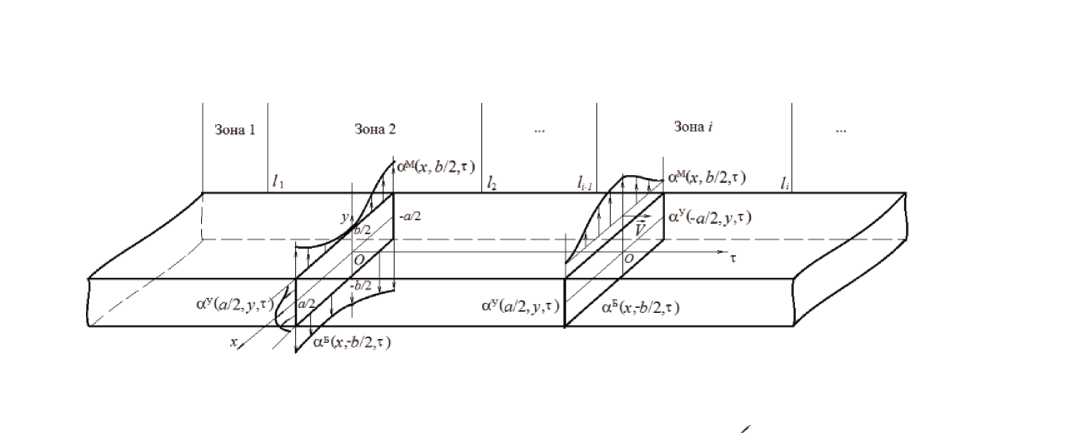
Рис. 1 . Схема перемещения фиксированного сечения во времени

введенные допущения, можно выполнить формализацию задачи для описания теплового состояния заготовки как бесконечного прямоугольного параллелепипеда с динамически изменяющимися граничными условиями третьего рода.

Для описания теплового состояния тела выберем уравнение теплопроводности с учетом выделения тепла кристаллизации [4]

c(T ) p ( T )

dTA^yj) ∂τ

L

C(T)

dS (x,y,T ) ∂τ

= I ( x ( t ) ^dTl^xyTl ) + I (4T ) ^dT(^x,^y,^T1 ), ∂x         ∂x       ∂y         ∂y

где y»-.-C) dx к?'™"-' <)

dX ( T (x ,y ,t )) ∂x

21X1x1:1 + x(t (x,y,T)) d'T dX / dT (x ,y ,t ) )2               d 2T (x ,y ,t )

dT A 8x ) + X(T(x-y-T»d.

^dX(T(x,y^,T)) ^dT(x,y^,T) , _w^_{z      AA}^d 2 ^{T ( x} ,y^,T)

----dy---aT- + X(T(x'y’T ”dy dX / dT(x,y,T) )2                d 2T(x,y,T)

dT A -ey— ) + X(T (x'y'т))   dy2.

При y E (—b ; b) ,x G (— a ; b) и при выполнении начальных условий в виде извест- 22 22

ной функции для описания температурного поля по фиксированному поперечному сечению тела T(x,y, 0) = f (x,y) , получаемой, как правило, эмпирическим способом, и граничных условий третьего рода для каждой грани заготовки, обеспечивающих несимметричность ее охлаждения:

-

ЭТ X(" ) ∂x

ЭТ

- X(" ) ∂x

-

ЭТ

Х(" ) TT ∂y

x =

x =

b

—

b

y =± a

— aM (x, b,)^. ^Ь.т) - U i ( t )] + ст

— а Б (x. - b.^Wx.- ^Ь,т) - U 2 (T )1

" 4 (x, 2 .t)     U 4 ( t )

-

100        100

^{— а}У (± a .у^,т) [" (± a. y.^T) ^{- и} з ^{( т} )] ^{+ ст}

" ⁴ (x. - 2 ,r)    U 2 (T )

-

100        100

"⁴ (± 2 ,У,т)    U^T )

-

100        100

Для описания теплового состояния тела введены обозначения: T(x,y,T ) - температура тела в точке с координатами (x, у) в заданный момент времени т , ° C; р(") - плотность рассматриваемого материала, из которого изготавливается заготовка, как функция от температуры в данной точке, м ³ / кг; L – скрытая теплота кристаллизации, Дж/кг; S – сечение жидкой фазы; Х(") - функция изменения коэффициента теплопроводности, Вт / (м • ° C); с(") - функция изменения коэффициента теплоемкости, Дж/(кг • ° C); U i (T ) - температура окружающей среды в текущий момент времени, ° C; ст — е пр ст - приведенный коэффициент излучения, соответствующий поверхности слитка, Вт/(м ² • ° C ⁴ ) ; е _пр - степень черноты поверхности слитка; ст о - коэффициент излучения абсолютно черного тела. Зависимости р(") , Х(") и с(") имеют эмпирическую природу и приведены в работах Маковского В.А.

Для определения функции для коэффициента теплоотдачи с поверхности тела примем функции в виде временного ряды со структурными изменениями, учитывающих переход зафиксированного сечения тела в заданную зону. Такие функции записываются соответственно для каждой поверхности тела:

^а Б ^(x. ^- |.^T) ^{— a}l^5(x. ^- b^,T) • ^z 1 ^{( t}

n —1

• <    ^T i )⁺ ^ ° i ^{( x}.

i =2

-

b

2,T) • Z i (T i —1 < T i ) +

+ a ’ (x,

-

b ⁿ

2 ^{,T )( t} > iT 1 ^T i ).

bb a (x. ^,T) — ai (x. ^,T) • zi(T

• <    T 1 ) + ’ f 1 a M (x.

i =2

^{+ a M (x}. ^b,T

b

2,T) • Z i (T i —1 < T i )+

n

^)(T > ^ ^T i ).

i =1

aa а (±^.у,т) — а1 (±^.у,т) • zi(T

’ —1

< ^T 1 ) ⁺ ^ ^{а У (}±2 .У^,Т ) • z i ^{( T} i — 1 <^T < ^T i ^{) +} i =2

n

^{+ а} У ⁽±I .y^{,T )( t} > ^^T i ⁾.

i =1

где α i – коэффициент теплоотдачи в i-й зоне охлаждения; n – количество зон охлаждения; z i – фиктивная переменная, определяющая переход в соответствующую зону водовоздушного охлаждения в выбранном режиме: Z i — 1 - при входе выбранного сечения в i-ую зону и Z i — 0 - при выходе сечения из i-ой зоны; T i - время прохождения заготовкой i-й зоны вторичного охлаждения.

2.    Моделирование динамики скоростных параметров

Среди параметров управления технологическим процессом непрерывной разливки стали наибольшее внимание уделяется выбору скорости вытягивания заготовки, определяющей динамику изменения граничных условий третьего рода. В ходе технологического процесса разливки стали возникает необходимость изменения скоростного режима в связи с заменой сталеплавильных ковшей на стенде при выводе МНЛЗ на рабочий скоростной режим, при остановке МНЛЗ на плановые профилактические ремонты. Динамика скоростного режима определяет условия охлаждения заготовки, в результате чего образуются пояса на поверхности, и создаются благоприятные условия для образования и развития внутренних дефектов [5].

На рис. 2 показан фрагмент одной из диаграмм изменения скорости вытягивания заготовки в течение одной серии. На диаграмме наблюдаются плановые изменения скоростного режима, которые чаще всего обусловлены ритмом работы предыдущих этапов обработки. На рис. 2 для указанных составляющих введены обозначения: 1 – S 1 i ; 2 – v i ; 3 – S 2 ; 4 – E i .

Согласно [6] плановые изменения скорости подразделяются на четыре типа. Первый тип переходного процесса – снижение скорости с одного установившегося значения до другого (разность скоростей > 0,1 м/мин). При этом процессе участок тела, находящийся в 1 и 2 зонах охлаждения, получает повышенное количество воды, в результате чего происходит его переохлаждение и повышается вероятность образования дефектов макроструктуры и поверхности слитка (см. рис. 2).

Второй тип переходного скоростного процесса – увеличение скорости с одного установившегося значения до другого (разность скоростей более 0,1 м/мин). Участок слитка, находящийся в 1 и 2 зонах охлаждения, получает меньшее количество воды, в результате чего происходит его разогрев и повышается вероятность образования внутренних и поверхностных дефектов, а также угроза раскрытия этих дефектов.

Рис. 2 . Фрагмент диаграммы изменения скоростного режима при непрерывной разливке стали в заготовки прямоугольного сечения

Третий тип переходного скоростного процесса – кратковременное снижение скорости до 0,1 м/мин на время смены погружных стаканов до 50 с с последующим увеличением до рабочего значения. При этом участок слитка длинной в 2 м, отлитый во время снижения скорости и охлаждаемый по существующей таблично-скоростной модели охлаждения, переохлаждается, и повышается вероятность образования дефектов макроструктуры и поверхности слитка.

Четвертый тип переходного скоростного процесса – снижение скорости с рабочего значения 0,6..1,0 до 0,1 м/мин на время смены промежуточного ковша (до 5 мин) с последующим увеличением до рабочего значения. Данный тип переходного процесса характерен тем, что имеет ≪ полный набор ≫ недостатков, присущих всем предыдущим рассмотренным процессам:

• •    неравномерная средняя плотность орошения поверхности сляба после выхода его из кристаллизатора на участке слитка длиной 4 м (разница более чем на 25 % между соседними метровыми участками сляба);

• •    резкое изменение, по отношению к соседней зоне, величины средней плотности орошения охлаждения участков сляба по длине зон вторичного охлаждения;

• •    очень велика (до 30 %) неравномерность регулирования плотности орошения в первой, второй и третьей зонах охлаждения на участке слитка длиной 1 м.

Все вышеперечисленные факторы негативно влияют на температурную ≪ картину ≫ тела. Кроме перечисленных участков изменения скоростного режима просматриваются участки диаграммы, на которых важную роль играет случайная компонента скорости. Природа этой случайной компоненты может быть разнообразной, и невозможно выполнить группировку или систематизацию источников возникновения этой составляющей.

Для снижения последствий переходных скоростных режимов предлагается построенная на основе экспериментальных и теоретических данных математическая модель для описания скоростных компонент. На ее основе проводится имитационное моделирование процесса разливки стали для изучения температурных полей затвердевающей непрерывно-литой заготовки и возникающих термических напряжений.

При моделировании скоростного режима непрерывной разливки стали авторами предлагается использовать временной ряд со структурными изменениями, включающий n частей по количеству технологических зон агрегата. Каждый из этих элементов временного ряда содержит трендовую, циклическую и случайную компоненты, соединенные по аддитивной модели:

n

v(t) = ^[viZi(Ti-i < T < Ti) + Ei + Sli] + S2, i=1

где v ( t ) — временной ряд для скорости вытягивания заготовки из кристаллизатора, м/с; v i – плановая составляющая скорости на заданном интервале времени τ i _- 1 ≤ τ ≤ τ i , м/с; z i – фиктивная переменная, определяющая переход из текущего временного интервала в следующий и принимающая значение 0 при выходе из текущего временного интервала и 1 – при входе в него; S 1 i – циклическая составляющая, обусловленная частотой качания кристаллизатора, S 2 – циклическая составляющая, обусловленная ритмом работы участков выплавки и доводки стали; E i – случайная компонента скорости.

Таким образом, выстраивается методика определения граничных условий третьего рода в динамике продвижения фиксированного сечения бесконечно протяженного тела и последующего моделирования его теплового состояния:

• 1.    определить скоростной режим на всей технологической линии зонального продвижения фиксированного сечения бесконечного тела;

• 2.    в каждый момент времени моделирования теплового состояния тела с учетом ≪исто-рии≫ скоростного режима определяется положение фиксированного сечения по металлургической длине;

• 3.    для определенного положения поперечного сечения выбирается расход охладителя по количеству установленных форсунок, расположения роликов на полотне и расходов охладителя;

• 4.    на основе расходов охладителя по технологическим параметрам форсунок идентифицируется функция коэффициентов теплоотдачи для заданного положения;

• 5.    выполняется решение уравнения теплопроводности с заданными граничными условиями третьего рода и начальными условиями, полученными на предыдущем шаге моделирования.

3.    Программная реализация модели бесконечно протяженного тела с учетом динамически изменяющихся граничных условий третьего рода

Решение уравнения теплопроводности с заданными начальными и граничными условиями выполнялось конечно-разностным методом на основе явной схемы с проверкой условий сходимости выбранного метода.

Программная реализация математической модели бесконечно протяженного тела с учетом динамически изменяющихся граничных условий была выполнена на базе программного продукта ≪ Steel & Speed ≫ . В программном продукте ≪ Steel & Speed ≫ можно выделить основные функциональные части, взаимосвязь между которыми приведена рис. 3.

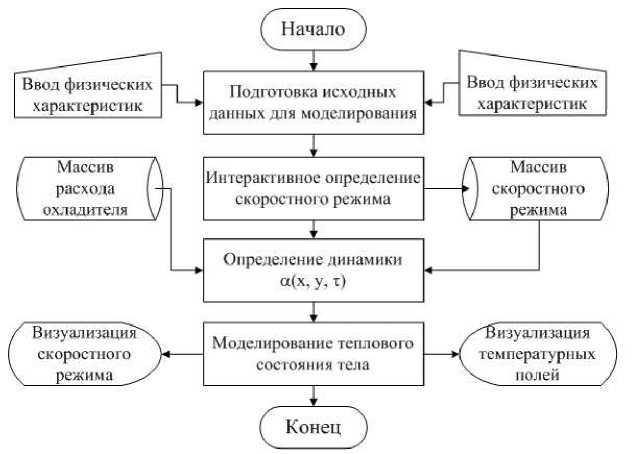
Рис. 3 . Функциональная схема взаимосвязи основных компонент программного продукта ≪ Steel & Speed ≫

Определение исходных данных подразумевает ввод или выбор набора физикохимических и технологических параметров непрерывной разливки стали. В качестве исходных данных для задания скоростного режима изменения граничных условий можно рассматривать первоначальную диаграмму скорости, на которой отображены результаты влияния компоненты, полученной по частоте качания кристаллизатора. Первоначальная скоростная диаграмма корректируется в интерактивном графическом режиме для компонент vi и S2 . В автоматическом режиме на основе математической модели добавляются компоненты случайной составляющей. В результате обработки скоростной диаграммы формируется обновленная зависимость для коэффициентов теплоотдачи с каждой поверхности бесконечно протяженного тела, для нее корректируется матрица расходов охладителя согласно существующим эмпирическим зависимостям и схеме расстановок форсунок.

Диаграмма плановой скорости вытягивания строится в интерактивном режиме, устанавливая заданную скорость в заданное время в течение всей разливки стали. График скорости имеет ступенчатый вид. Введенные значения скорости отображаются в таблице. Предусмотрена возможность отменять и возвращать последние введенные значения скорости (рис. 4). Последнее значение скорости должно соответствовать тому времени, в течение которого необходимо произвести расчет.

На основе принятых исходных данных и скорректированной скоростной диаграммы выполняется математическое моделирование теплового состояния тела. Результаты моделирования представляются графически в виде двух- и трехмерных диаграмм (рис. 4 – 7).

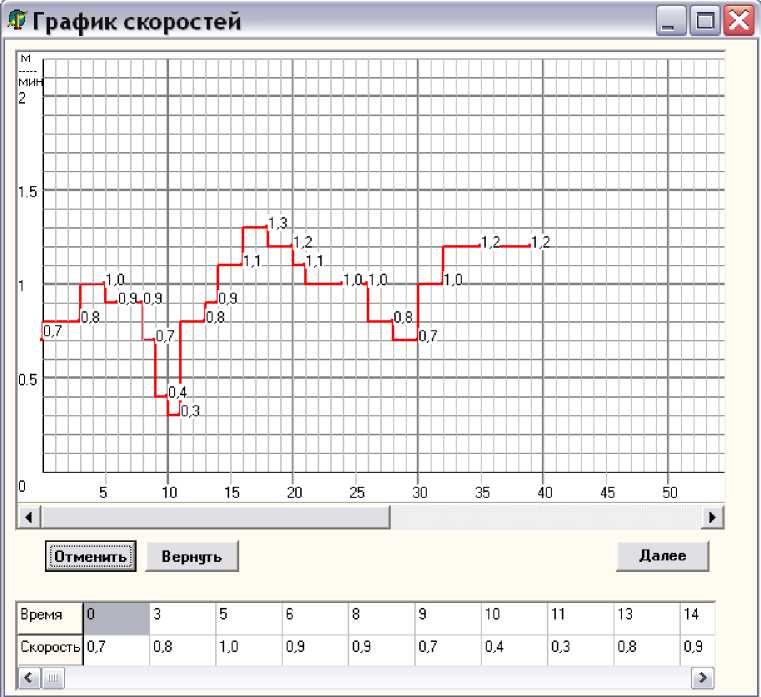
Рис. 4 . Вид диалогового окна для определения плановой компоненты в интерактивном режиме

Программный продукт использует многооконный пользовательский интерфейс, систему главного меню и панель инструментов для интерактивного диалога с пользователем.

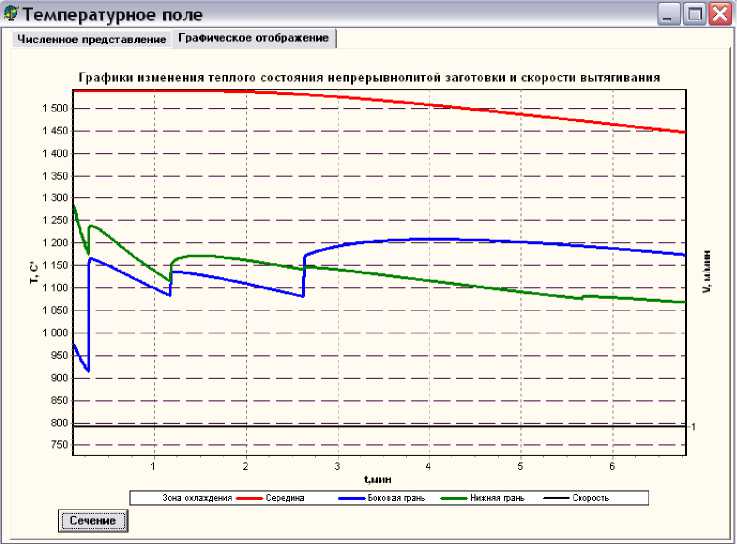
Рис. 5 . Вид окна программного продукта с результатами изменения теплового состояния заготовки при неизменной скорости вытягивания в пределах каждой зоны

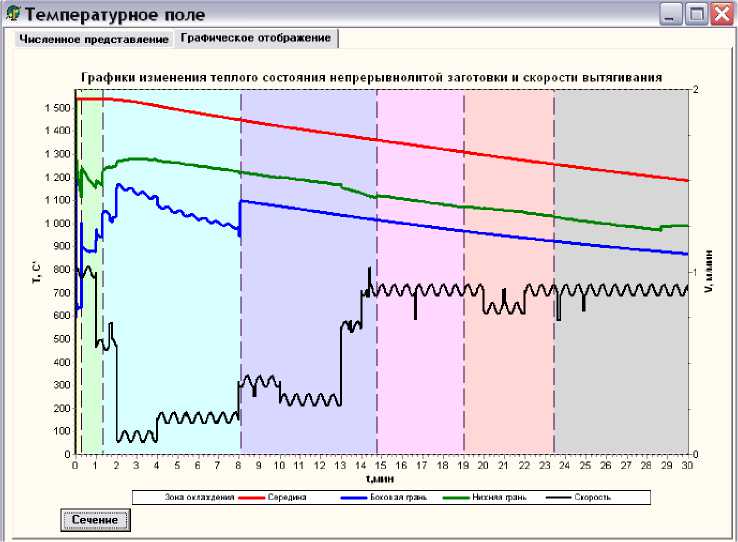
Рис. 6 . Вид окна программного продукта с результатами изменения теплового состояния заготовки с участком резкого падения скорости вытягивания в пределах одной зоны

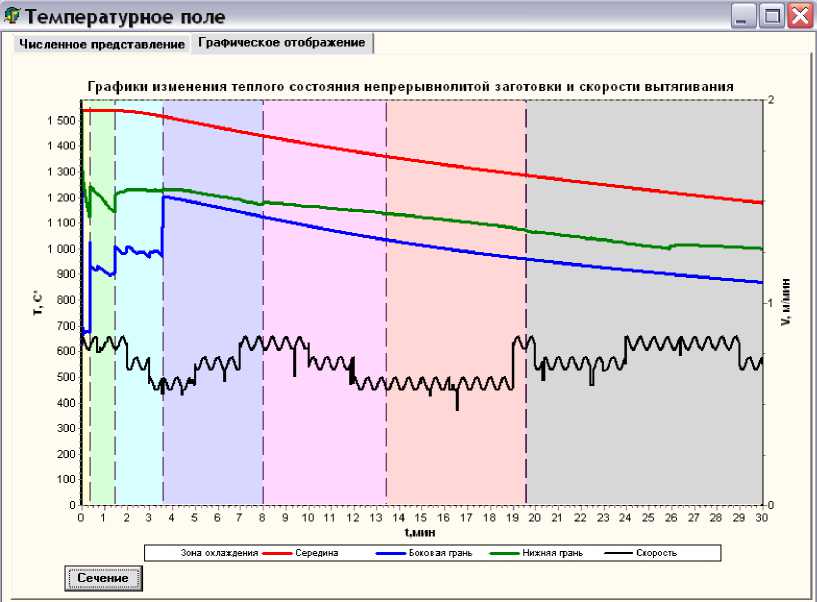
Рис. 7 . Вид окна программного продукта с результатами изменения теплового состояния заготовки при плавных небольших изменениях скорости вытягивания

4.    Заключение

По результатам математического моделирования теплового состояния бесконечно протяженного тела с динамически изменяющимися граничными условиями третьего рода можно сделать следующие выводы:

• 1.    принятые допущения для математического моделирования теплового состояния непрерывнолитой заготовки позволили представить ее в виде бесконечного прямого параллелепипеда с динамически изменяющимися граничными условиями третьего рода;

• 2.    учет динамики скорости вытягивания бесконечного тела необходим при исследовании теплового состояния его поверхностных слоев глубиной залегания не более 1 см;

• 3.    температурные колебания, возникающие в затвердевших поверхностных слоях заготовки, представляющей собой бесконечно протяженное тело, с амплитудой до 30 ° приводят к термоциклированию, в результате которого формируется мелкозернистая структура глубиной от 0,003 до 0,01 м, которая при увеличении амплитуды колебаний разрушается, и в ней формируются сетчатообразные трещины;

• 4.    построенная математическая модель может быть использована в автоматизированной системе управления производства непрерывнолитых заготовок при корректировке управления в локальном контуре скорости вытягивания для получения заданного качества продукции.