Моделирование теплового состояния катодных узлов сильноточных плазменных систем

Теплофизическое состояние термоэмиссионных катодов определяет работоспособность и ресурс их работы. Теоретический подход к решению тепловой задачи изложен в [1, 2]. В этих работах тепловая задача для термоэмиссионного электрода рассмотрена в постановках наиболее приближенных к реальным условиям. Решено уравнение теплопроводности для системы «вставка — обойма» в целом и показано, что механизм разрушения катода в значительной степени обусловлен неоднородностью тепловых потоков внутри электродного узла. Однако в работах не учтен ряд важных факторов, таких как зависимости теплоэлектрофизических характеристик материалов от температуры, распределения тока и джоулева тепловыделения в объеме электрода, нелинейность граничных условий задачи ввиду излучения и теплообмена с плазмообразующим газом. В работе [3] решена задача о протекании тока в системе двух сопряженных элементов.

В данной работе представлены результаты численного моделирования теплового состояния составного катодного узла с учетом джоулева тепловыделения, конвективного и лучистого теплообмена.

Постановка задачи

Теоретическое исследование стационарного теплового состояния катодного узла состоит в совместном решении уравнения теплопроводности и уравнения неразрывности тока (уравнения Лапласа) с учетом джоулева нагрева:

1 д r d r

r 2 ( T^T о r

a

+— az

aт   1 ( и и 2   1 ( и и 2   „

дт )— +-I — I +-I — I = 0

az J p (ar J p (az J

1 ⁹ r ⁹ U r a r _ р ( т ) a r

.                       ' U

az _ p(t) az

Уравнения решаются для системы из двух сопряженных элементов (катода и обоймы). На рис. 1 показана расчетная модель катодного узла. Катодный узел обладает цилиндрической симметрией и состоит из вольфрамовой катодной вставки (I) и медной обоймы (II). В работе расчет проводился для следующей геометрии:

L 1 = 3 см, L h = 1 см, L c = 2 см, R 1 = 0,25 см, L 2 = 1,5 см, R 2 = 1,5 см.

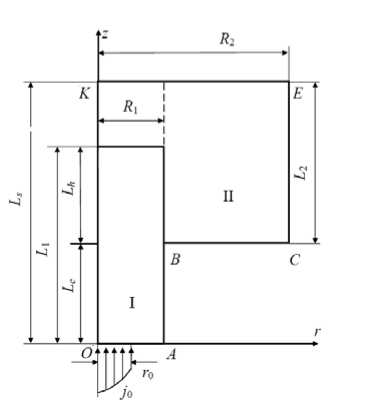
Рис. 1. Модель катодного узла. I — катод, II — обойма.

Дуговой разряд горит в атмосфере аргона при давлении P = 10⁵ Па и токовой нагрузке I = 300 A, интегральный тепловой поток Q = 340 Вт, радиус катодного пятна r 0 = 0,1 см.

Граничные условия для уравнения теплопроводности на рабочем торце катода ( OA ) с учетом конвективных и радиационных составляющих теплообмена с

окружающим газом выглядит следующим образом:

21 (T)

а т ( r ,0 ) d z

< £ 1 CT T 4

E 1 O T ⁴

- q o , 0 <  r <  r o

+ ag (T - Tg ) ro < r < ^1

Граничные условия для уравнения неразрывности тока на том же торце принимают следующий вид:

1    а и ( r ,o )

P1 (t )   az

—

I

™"0

0 <  r <  r 0

0, r 0 <  r <  ^ 1

Граничные условия на остальных поверхностях катодного узла представлены в таблице:

Таблица

Граничные условия к уравнениям теплопроводности и неразрывности тока

	Уравнение теплопроводности	Уравнение неразрывности
AB	2 1 T )    d r   - a g ( t T g ) £ 1 c T	d U ( R 1 , z ) = 0 5 r
BC	'(T}?^ - a g ( t - T g )	d U ( r , Lc ) = 0 d z
CE	2 2 ( TfT ^'— « g 'T — T g )	U ( R 2 , z ) - 0
EK	T ( r , L s ) - T 0	U ( r , Ls ) - 0
KO	d T ( 0, z ) = 0 d r	d U (0, z ) = 0 d r

В таблице приняты обозначения: Е 1 — степень черноты (равный 0,3); 2 1,2 ( T ) — коэффициент теплопроводности; р 1,2 ( T) — удельное электросопротивление вольфрама и меди; U — потенциал электрического поля; I — разрядный ток (300 А ); с — постоянная Стефана-Больцмана (5,6720^-12 Вт/см²К⁴); a g — коэффициент теплоотдачи газу (3700 Вт/м ² К); T 0 — начальная температура катода (300 К); T g — температура газа (300 К).

Результаты и их обсуждение

На рис. 2 слева показаны эквипотенциали и линии тока в объеме катодного узла. Моделирование проводилось в среде Comsol Мultiphysics. Распределение плотностей тока во вставке неоднородно. Большие градиенты плотности тока локализованы в области катодного пятна. В той части вставки, которая находится в обойме, происходит существенное уменьшение плотности тока, что связано с уходом тока через боковую поверхность электрода. На рис. 2 справа показаны изотермы. В области катодного пятна электрод нагревается до максимальной температуры приблизительно 2890 К. На изотермах, также как и на эквипотенци-алях, видны резкие разрывы производных соответствующих величин в области контакта сопряженных элементов, состоящих из разных металлов. В выступающей части вставки изотермы достаточно быстро выравниваются по поперечному сечению, поэтому можно предположить, что для длинных и тонких катодов ( L c >>  R 1 , r о ~ R 1 ) тепловую задачу можно рассматривать в одномерном приближении.

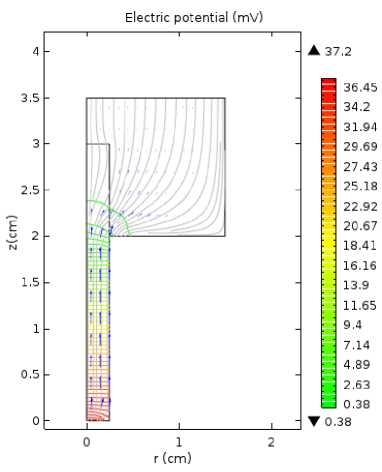
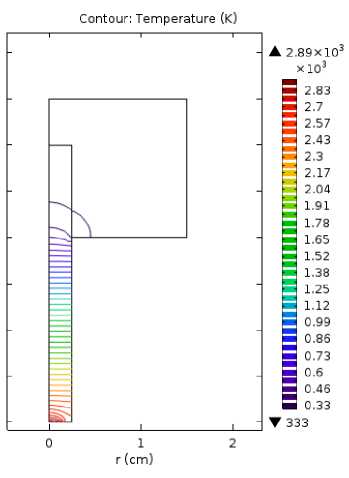
Рис. 2. Эквипотенциали и линии тока — слева; изотермы — изотермы.

На рис. 3 показаны осевые распределения температур, полученные варьированием коэффициентов р i , е i , a g в уравнениях, указанных при постановке задачи. Распределение температуры на кривой 1 соответствует исходной постановке задачи: с учетом джоулева тепловыделения и теплообмена путем конвекции и излучения. Температурное поле, рассчитанное таким образом, согласуется с экспериментальным данными [4]. Остальные распределения получены при упрощенной постановке задачи. Кривая 2 получена при расчете без учета джоулева тепловыделения ( ρ 1 = 0), а также без учета тепловых потерь за счет излучения ( е i = 0) и конвекции ( a g = 0). Видно, что профиль распределения сильно отличается от предыдущего случая. Максимальная температура в области катодного пятна при такой постановке существенно выше — около 3600 К.

Учет по отдельности только джоулева тепловыделения (р i ^ 0, е i = 0, a g = 0; кривая 3), или же конвективного и лучистого теплообменов с поверхности катода (p i = 0, E i # 0, a g + 0; кривая 4), приводит к еще большим отклонениям в распределении температуры. Так, например, максимальные температуры на кривых 1 и 3 отличаются на ~ 1700 К. Таким образом распределения 3 и 4 наглядно показывают сильное влияние джоулева нагрева и комбинированного теплообмена с поверхностью на тепловое состояние катода. При этом вклад каждого из упомянутых выше факторов в энергобаланс зависит от величины разрядного тока. При токовой нагрузке I <  300 A заметно больше влияния джоулева тепловыделения. При увеличении тока доля джоулева тепловыделения в энергобалансе повышается и при I >  500 A объемный источник тепла преобладает над энергией, рассеиваемой излучением и конвекцией.

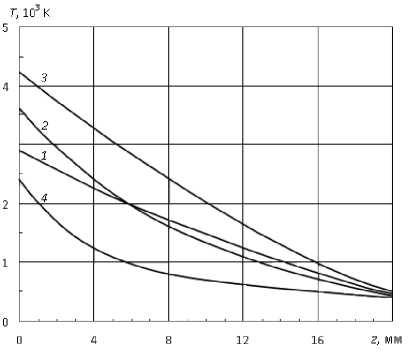
Рис. 3. Распределение температур вдоль оси катодного узла.

Заключение

Проведено численное моделирование тепловых процессов в катодном узле цилиндрической симметрии. В постановке задачи для катода, как системы двух сопряженных элементов (электродной вставки и обоймы), учтены локальное джоулево тепловыделение, конвективная и лучистая составляющие комбинированного теплообмена, нелинейные зависимости тепло- и электрофизических свойств от температуры. Показано, что пренебрежение джоулева тепловыделения в энергобаланс катода приводит к большим погрешностям в определении температурного поля катодного узла.