Моделирование тепловых процессов при плазменной обработке по кольцевой траектории

В настоящее время в технологии машиностроения используется широкий спектр физико-химических методов воздействия и модифицирования материалов и изделий, такие как электрофизические методы обработки и физико-химические технологии [1-3]. Среди них немаловажное место занимают плазменные технологии, в частности плазменная термообработка, сварка и наплавка.

нестационарным. Поэтому при расчете характеристик термических циклов в данном случае необходимо учитывать зависимость температуры и от координат и от времени во всем периоде сварки или наплавки. Криволинейные траектории движения источников теплоты используются при сварке, наплавке, напылении и поверхностной термической обработке с целью получения заданных свойств изделия. Однако особенности тепловых процессов при сварке соединений с криволинейными швами изучены недостаточно. При сварке криволинейных швов поле тепловых потоков значительно сложнее, чем при сварке прямолинейных швов, что отражается на термических циклах исследуемых точек [9].

В данной работе приводятся результаты моделирования процессов нагрева при плазменной обработке круглых образцов из стали 19ХГНМА. Диаметр образцов составлял 52 мм при толщине 10 мм. Моделирование нагрева проводилось без и со сканированием плазмотрона на вращающийся образец с угловой скоростью 220о/мин (0.064 рад/с). Для анализа был выбран ток дуги 85 А. Моделирование проводилось также с учетом и без учета влияния конечного диаметра образца – учитывалась влияние одной внешней границы образца.

Размах колебаний сканирования при моделировании составлял 9 мм, частота сканирования – 0,4 Гц (циклическая частота 2.6 Гц). В этом случае скорость сканирования плазменной дуги составляет 7-8 мм/с. Диаметр сопла плазмотрона составлял 2,4 мм. При диаметре сопла плазмотрона 2,4 мм эффективный радиус пучка принимался R_эфф = 1,4 R_c = 1,68 мм. Расчеты проводились в пакете Mathcad 14 в декартовой системе координат.

При моделировании время воздействия плазменной дуги определялось как _ n-к tm = Q    , вращ

где Q вращ - угловая скорость вращения образца; n - численный коэффициент, определяющий поворот образца относительно начала вращения ( 1 / 4 ; 1 / 2 ; 1 и т.д.).

При решении тепловой задачи будем считать, что тело представляет собой плоский слой, а плазменная дуга - поверхностный нормально распределенный источник теплоты. Из-за сложности постановки задачи не будем учитывать поверхностную теплоотдачу.

Очень часто при моделировании тепловых полей при сварке и наплавке используется метод источников (метод функции Грина), в котором реализуется принцип суперпозиции полей от элементарных источников теплоты. В частности в работе [3] на основе этого было получе- но выражение для расчета температурного поля при воздействии сканирующей плазменной дугой в подвижной системе координат:

T(x,y,z,tm) =

Рэ t 1

—— --exp

ЫН Jt+1„

(x + v„,t)2 + [y- A - sin[to-(tm -t)]]2

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_

4 - a - (t +10)

C    f niz)     f   2,2 at)  1H          nig

1 + 2-LСМЫ-exp|-ni -AT IATJ q1(c)cosAAdc i=i   kH 7    k H 7 Рэ 0          H dt + T„

exp

где P_Э=h^P_Д - эффективная мощность плазменной дуги , п - эффективный к. п. д. дуги, который в большинстве случаев можно принять равным 70%; H - толщина плоского слоя; t m - время нагрева; У_а в - скорость движения заготовки; ю =2 п / Т скан - частота сканирования дуги; Т с _кан - период сканирования; амплитуда сканирования A = D] 2 ; D - размах колебаний; t ₀ = К^ /4 - a ; T 0 - начальная температура; q 1 (z) - функция интенсивности источника теплоты по толщине. Будем считать, что источник нагрева поверхностный и согласно [2] для такого источника интеграл под суммой равен Р Э . При этом мощность дуги определяется через ток и напряжение дуги Р _д = I _д - и _д . На основе выражения (2) в работе [8] была разработана программа расчета и проведено моделирование процесса плазменнопорошковой наплавки сканирующей дугой при формировании прямолинейных дорожек.

В выражении (2) под экспоненту входят выражения, описывающие траекторию движения источника нагрева

xu(t) = vde -1 и yu(t) = A - sin(^-1). (3)

Первое из этих выражений описывает поступательное прямолинейное движение образца относительно источника нагрева, а второе - сканирование плазменной дуги. При термообработке, сварке и наплавке кольцевых швов задача усложняется, так как на сканирование накладывается вращение образца. В этом случае при обработке теплосодержание в центре образца будет возрастать интенсивнее, чем при поступательном движении. Для решения задачи нагрева в таких случаях функции траектории источника (3) можно задать в параметрическом виде. Без учета задержек плазмотрона в крайних точках при сканировании также как и в предыдущем случае предлагается представить функции траектории источника через тригонометрические функции в виде:

xu (t) = [R0 - A - sin(^ - t)] - C0S(Qвращ - t) , (4)У u (t) = [R0 - A - Sin(^ - t)] - Sin(Qвращ - t) , (5)

где R 0 - расстояние от оси вращения образца до середины дорожки сканирования плазменной дуги (рис. 1); Q вращ - угловая скорость вращения образца; ю - циклическая частота сканирования дуги. Период сканирования при этом Т_ска „ = 2 л/ю = 2 - D[v_CKaH . При частоте сканирования ю = 0 данная кривая вырождается в окружность.

Таким образом, заменив в (2) функции тра- ектории движения источника, используя выра- жения (4)-(5), получим

T(x,y,Z,t m ) =

Рэ ' ■ 1

—— --exp ⁴кШ ^{J t} + 1 „

^[ x - [ К „ - A ■ sin( ®. (t m - t)) ] - COS^ ,, - (t m - t))f 4 - a - (t + 1 „ )

[ y - [ R o - A - sin( rn - (t m - 1)) ] - sin( n„„ - (t m - 1)) ] ² 4 - a - (t + t o )

1 1              f n iz ^      f at ^ 1               n ic . I_

11 + 2 - L cos I — I - exp | -п i - — I - —J q , ( ; )cos-Ad ; dt + T , .

L       i = 1     k ^H 7 k ^H 7 ^Р Э 0 ^H   _|

В приведенном выражении расчет температурного поля ведется в системе координат с началом в центре вращения образца.

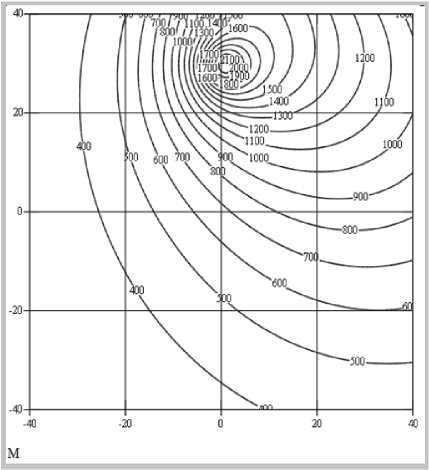
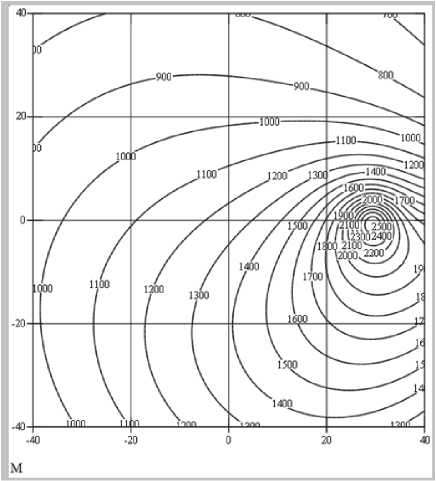
Результаты расчетов тепловых полей по поверхности зоны обработки кольцевых дорожек в виде изотерм представлены на рис. 2.

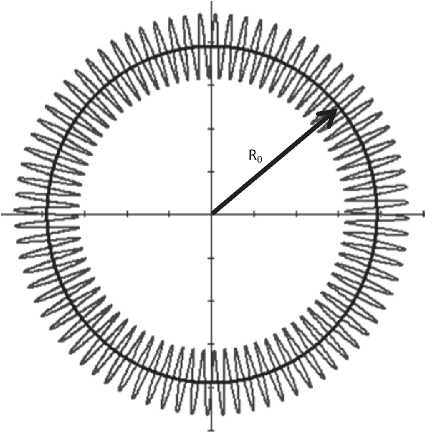
Рис. 1. Траектория движения источника нагрева (плазменной дуги) при обработке/наплавке кольцевых дорожек

a

б

в

г

Рис. 2. Распределение тепловых полей по поверхности стали 19ХГНМА при плазменном нагреве без сканирования на разных углах поворота: а) ф= 0 ° ; б) ф =90 ° ; в) ф =180 ° ; г) ф =360 °

Из рисунка 2 видно, что по мере вращения образца при нагреве или наплавке по кольцевой траектории тепловое поле охватывает все большие области образца, что приводит к повышению теплосодержания в нем и росту его температуры.

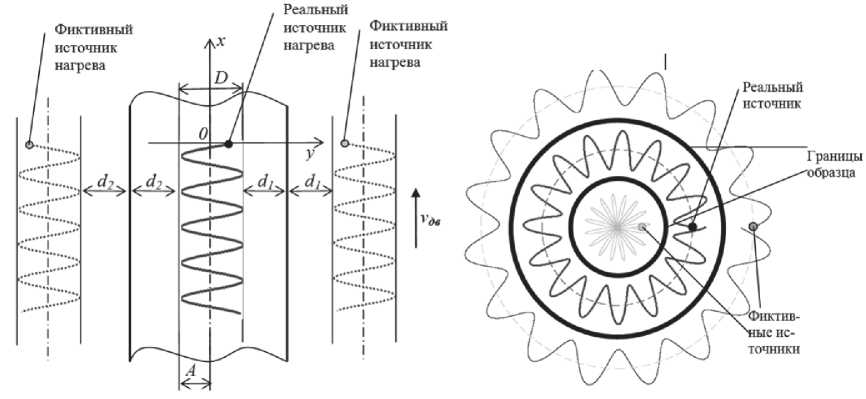
Конечные размеры образца можно учесть с помощью метода отображения [5, 7], вводя фиктивные источники нагрева (рис. 3).

Фиктивный источник нагрева располагается симметрично реальному источнику относи- тельно края образца и движется в противофазе с ним. В модели предполагается, что границы образца адиабатические. На рисунке D и A – размах и амплитуда сканирования дуги, а d1 и d2 – расстояния от края дорожки сканирования до края образца.

Схемы распределения реального и фиктивного источников нагрева при нагреве прямолинейных и кольцевых дорожек показаны на рис. 3

С учетом действия фиктивных источников выражение (6) примет вид:

a

б

Рис. 3. Схема расположения реального и фиктивных источников нагрева при нагреве сканирующей дугой:

а – нагрев при прямолинейном движении; б – нагрев по кольцевой траектории

exp

P ^{t m}m 1

^T ( x , У , z , mm ⁾ = .        -----

4ПШ t + 1 ₀

• exp

^[ x - [ R q - A • ^Sin Q ( t _m ^- t ⁾) ]‘ COS⁽ Q epa^ • ⁽ t m ^- t ^f _ ⁴ • a ■ ⁽ t + t Q ⁾

[ y ^{- [} R Q ^- A • ^Sin( ^ ^ ⁽ t m ^- t ^{)) ]} • ^Sin( Q _вра_Щ • ⁽ t m ^- t ^{)) ] 2}

•

4 • a • ( t + t ₀)

+

> ■

+ F_x( t ) + F ₂( t )

^    ( niz )      ( _г a at А 1 H / x

1 + 2 • >, COS| — I • expl - n i • — I •— I qi(^)COS i=1    V H ) V H ) P3 0

^d ^ dt + T_o

H 9      0

4 приведена схема расположения источника нагрева в разные моменты времени при нагреве с вращением цилиндрического образца. Схема приведена без отображения возможного сканирования источника нагрева.

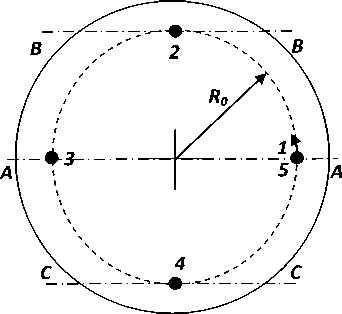
Рис. 4. Схема расположения источника нагрева в разные моменты времени при нагреве с вращением цилиндрического образца

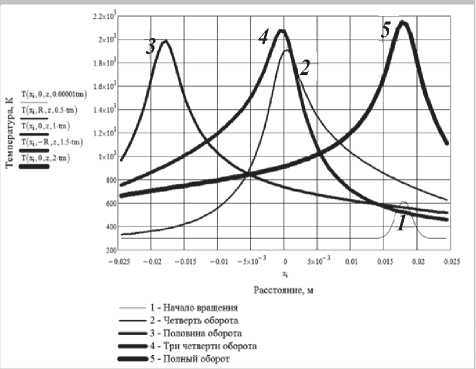
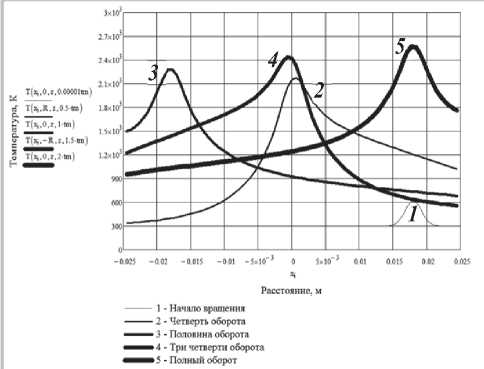
a

б

Рис. 5. Температурные кривые при плазменном нагреве стали 19ХГНМА без сканирования: а – без учета внешней границы образца; б – с учетом внешней границы образца

Цифры на рисунках соответствуют температурным кривым при различных углах поворота нагреваемого образца, которым соответствуют положения источника нагрева на рис. 4. При этом температурные кривые, построенные в прямоугольной системе координат, приведены для соответствующих сечений плоскостями, приведенными на рис. 4. Так кривые 1, 3 и 5 соответствуют сечению А-А на рис. 4; кривая 2 – сечению В-В; кривая 4 – сечению С-С соответственно. Хорошо видно, что из-за непрерывного роста теплосодержания выравнивания температур не происходит при нагреве с вращением, что может привести, например, к изменению ширины сварного шва или геометрии валика при наплавке, а также глубины проплавления подложки, что подтверждается экспериментально в [6]. В данной работе приводятся результаты исследований по плазменной наплавке порошка Stellite 190 на цилиндрические образцы из стали 19ХН3МА .

Показано, что в процессе наплавки по мере прогрева образца наблюдается изменение ширины наплавленной дорожки за счет более интенсивного растекания расплава (рис.

• 6) . Экспериментально было установлено, что ширина наплавленной дорожки растет по мере поворота образца, а ее высота снижается. При этом также растет глубина проплавления подложки [6].

С ростом теплосодержания растет температура в зоне наплавки и при токе дуги 100 А наблюдается интенсивное образование пор, особенно для образца толщиной 10 мм (рис. 6, в). Образование пор может быть связано с выделением газа, попадающего в наплавленный слой вместе с порошком, либо с испарением более легкоплавких элементов.

В процессе наплавки проводилось также измерение температуры в центре образца с помощью термопары. В таблице 1 приведены расчетные и экспериментальные данные по температуре центра образца и глубины проплавления подложки при разных углах поворота в процессе плазменной наплавки Stellite 190 на цилиндрические образцы из стали 19ХН3МА при токе дуги 85 А. Расчеты проводились с использованием выражения (7) для толщины заготовки Н=10 мм при наличии только внешней границы образца.

a                       б                  в

Рис. 6. Образцы с наплавкой Stellite 190 на цилиндрические образцы из стали 19ХН3МА при различных токах плазменной дуги [6]:

а - I =70 А; б - I =85 А; в - I =100 А

Таблица 1. Температура и глубина проплавления подложки при плазменной наплавке порошка Stellite 190 на сталь 19ХН3МА

Угол поворота образца	00	900	1800	2700	3300
Т, К центра образца, расчетная	300	645	925	1170	1264
Т, К центра образца, эксперим.	361	580	861	1043	1293
Глубина проплавления подложки, расчетная, мм	0.7	1.5	1.6	1.8	2.2
Глубина проплавления подложки, экспериментальная, мм	0.8-0.87	1.0-1.5	1-1.5	1.5-1.6	1.6-1.8

Из таблицы хорошо видна определенная корреляция между расчетными и экспериментальными данными.

Включение сканирования приводит к снижению максимальной температуры (табл. 2) и при этом наблюдается менее интенсивный рост цевой траектории. В модели можно учесть сканирование плазменной дуги, а также конечные размеры обрабатываемой заготовки.

На основе теплофизического моделирования показано, что при плазменном поверхностном нагреве цилиндрической заготовки из-за

Таблица 2 . Максимальная температура в зоне нагрева в зависимости от угла поворота цилиндрической заготовки

Режим обработки Угол поворота 90о 180о 270о 360о Без границы, без сканирования 1908 1995 2073 2153 Без границы, со сканированием 1618 1808 1920 1945 С границей, без сканирования, Н=10 мм 2168 2300 2435 2580 С границей, без сканирования Н=15 мм 1706 1764 1885 1978 С границей, без сканирования Н=20 мм 1406 1415 1506 1578 С границей,со сканированием 1848 2076 2275 2320 температуры с ростом угла поворота. Анализ показывает, что краевой эффект (наличие границы) оказывает большее влияние на изменение температуры при нагреве с вращением заготовки, чем включение режима сканирования плазменной дуги. Расчеты также показали, что существенное влияние на динамику температуры в процессе нагрева с вращением оказывает толщина цилиндрической заготовки. При этом с ростом ее толщины различие в максимальной температуре на начальных периодах обработки и в конце снижается, поскольку часть тепла отводится вглубь заготовки. Так при нагреве заготовки толщиной Н=10 мм различие в температуре после четверти оборота (90о) и после полного оборота (360о) 420 К, в то время как при толщине заготовки 20 мм аналогичное различие составляет уже менее 200 К.

ВЫВОДЫ особенностей теплоотвода наблюдается существенный рост теплосодержания в нем, что неизбежно может сказаться на качестве процесса сварки или наплавки. На основе моделирования установлено, что на процесс изменения температуры при нагреве по мере вращения заготовки влияют конечные размеры образца, а также включение режима сканирования плазменной дуги. Наиболее существенное влияние оказывают конечные размеры образца (наличие внешней границы и толщина заготовки).

Проведено сравнение расчетных и экспериментальных данных по температуре нагрева и глубине проплавления подложки при плазменной кольцевой наплавке Stellite 190 на цилиндрические образцы из стали 19ХН3МА, которое показало корреляцию расчетных и экспериментальных данных. При этом наблюдается рост температуры, а также глубины проплавления подложки по мере нагрева при вращении.

Предложена математическая модель процесса нагрева цилиндрических заготовок при плазменной обработке, позволяющая проводить  1.

анализ тепловых процессов при поверхностной термообработке, сварке или наплавке по коль-