Моделирование термического режима литосферы Земли как фактора геодинамических угроз

ВЕСТНИК 2017

Температурное поле литосферы и геодина-мические угрозы12

Температура – важный параметр состояния вещества континентальной литосферы на- шей планеты. От нее зависят многие физические свойства горных пород, теплоперенос в глубинах Земли, инициируемый разностью температур, она является главным геодинамическим механизмом эволюции планеты [1].3Поэтому пространственное распределение температурного поля континентальной литосферы является определяющим при оценке количественных характеристик геодеформационных процессов, сказываю-

ВЕСТНИК 2017

щихся на геодинамических рисках, вызывающих землетрясения, извержения вулканов и другие земные катастрофы. В то же время, информация о современном температурном режиме Земли является одной из важнейших нерешенных проблем геофизики [2]. Основную информацию о тепловом режиме континентальной литосферы дает геотермический метод, основанный на изучении распределения по поверхности Земли плотности теплового потока и восстановления температуры в недрах путем решения обратной задачи для уравнения теплопроводности [3].

Термический режим океанической литосферы также во многом характеризует проявления опасных природных катаклизмов, опасных для судоходства, шельфовой добычи полезных ископаемых и жизнедеятельности населения островных государств и поселений, континентальных окраин.

Сейсмичность, вулканизм, цунами, торнадо и другие высокорисковые угрозы, обусловленные термическими факторами океанической литосферы, постоянно подстерегают человека и объекты производственной деятельности, расположенные в океанических районах и переходных зонах от континента к океанам.

Масштабность проблем, связанных с возникновением и реализацией геодинамических угроз со стороны океанической литосферы, выразилась в проведении ее углубленных исследований как на национальном, так и на межнациональном уровнях.

Особый интерес при этом представляют работы по математическому моделированию температурного поля океанической литосферы. При построении моделей распределения ее глубинных температур используются результаты геологических, сейсмических, петрологических, геотермических, магнитных, электромагнитных и гравиметрических исследований. Однако в силу своей сложности проблема состояния и динамики температурного режима океанической литосферы до сих пор таит в себе множество нерешенных вопросов.

Таким образом, важным является то, для какого типа литосферы проводится расчет распределения температуры – океанической или континентальной. В зависимости от этого рассмотрим две различные математические модели.

Описание модели температурного поля континентальной литосферы

Рассмотрим математическую модель, предложенную авторами для количественных оценок значений температуры на различных глубинных уровнях земной коры и построения простран-

ственных распределений температур на этих глубинах, при изучении термического режима континентальной литосферы Земли. Запишем уравнение теплопроводности:

a t   a (, a t A a (, a t A

pc— =—I k— 1 + — k— 1 +

dt dx V dx ) dy V dy )

d ( d T A

+vI k^T l ⁺ A ( ^x , y,z , t ),                   (1)

dz V dz )

где ρ – плотность, c – теплоемкость, T – температура, k –коэффициент теплопроводности, A – генерация тепла в единице объема, t – время.

Направляя ось z вертикально вниз и полагая (в первом приближении), что T и A не зависят от x и y , приходим к случаю одномерной задачи:

d T 6(6 T A pc— =    k    + A (z, t).              (2)

6t 6z V 6z )

Поскольку в дальнейшем расчеты будут вестись для глубин не более 100 км (толщина континентальной литосферы), то кривизной Земли пренебрежём. В качестве граничных условий при решении уравнения (2) можно взять температуру T ₀ и тепловой поток Q ₀ на поверхности Земли. Сложности существуют при определении начальных условий. Если температуру U считать от T 0 = const до U = T - T ₀ , то решение уравнения (2) при постоянных ρ , c и k при начальном U ( z , 0) = 0 и граничных условиях U (0, t ) = 0, U ( да , t ) ^ да определяется соотношением:

U ( z , t ) =

2 4П

t да

I d T J 00

h

t - т

( exp

V

ri) 4h2(t -т))

- ^

^ - exp

(5+z)L_ ] 4 h 2( t - т))

A ( Z , T ) d z ,

где h ² = ^k/ . p c

Как показали исследования, для глубин менее 100 км температурный режим можно считать стационарным, полагая A не зависящей от времени, что связано с достаточно постоянной и медленной генерацией тепла, обусловленной большим возрастом Земли. Таким образом, при оценке современной температуры на глубинах до 100 км уравнение (2) принимает вид:

d (1 6T)       .

k— l = - A (z). dz V dz )

Полагая k некоторой усредненной постоянной по всей глубине литосферы, для решения уравнения (4) необходимо знать вид функции A ( z ). В отношении функции A ( z ), входящей в (4), предположим, что объемная теплогенерация по-

род литосферы экспоненциально убывает с глубиной в соответствии с соотношением [2]:

A ( z ) — A exp

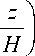
где A ₀ - константа, равная 3 - 10 6 Вт/м³, H - толщина литосферы.

В этих предположениях решением уравнения (4) является функция следующего вида:

T ( z ) = — C

AY exp ^f— HH J + C 2 z + C з ,    (6)

где C ₁ , C ₂ , C ₃ – коэффициенты, определяемые через граничные условия.

В качестве граничных условий определим следующие соотношения:

T ( z )| z = o = T ,; k о T '( z )| z = o = Q o ;

T ( z )| z — h — T h ,

где T ₀ , Q ₀ , k ₀ – температура, тепловой поток и коэффициент теплопроводности на дневной поверхности, а T_H – температура на границе литосфера – литосферная мантия.

Подставляя функцию (6) в граничные условия (7), получим систему уравнений с тремя неизвестными C ₁ , C ₂ , C ₃ :

A 0 H

1    7      +   3      0, k0

^ C A o H — Q o ,

—I

A 0 H ²

2.7183 - k_H

+ C ₂ H + C ₃ = T_H ,

где k_H – коэффициент теплопроводности на границе литосфера – литосферная мантия.

Разрешая систему уравнений (8) относительно неизвестных коэффициентов, приходим к следующим соотношениям:

C — Q -,

• ^{1   A} 0 ^H

_ Th — T o _ f 1         1      )

C 2                  Q<                             ,

• ²    H \ k_n 2.7183 - k_H

0 H

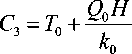
Таким образом, с помощью выражения (6) с учетом соотношений (9) можно рассчитать пространственное распределение температуры для континентальной части литосферы Земли применительно к задачам оценки геодинамических рисков [4; 5]. Для этого необходимо владеть ин- формацией по пространственному распределению величин поверхностной температуры, температуры на границе литосфера – литосферная мантия, поверхностного теплового потока и по- верхностного коэффициента теплопроводности.

Описание модели температурного поля океанической литосферы

Распределение температуры в океанической части литосферы рассчитывалось в зависимости от ее возраста в рамках модели остывающего полупространства [6] в соответствии с соотноше- нием:

Tizl z lo. — erf f 3Z z ^)

T H — T o      1 2 ^[Ft J

где T_H – температура на границе литосфера – литосферная мантия (принималась равной 1717.15°K), x - коэффициент температуропроводности (принимался равным 10^–6 м²/с [6], erf – функция ошибок, t – возраст литосферы.

При реализации этой модели важным этапом является организация вычисления значений функции ошибок erf. Имеются таблицы значений этой функции, но они содержат только дискрет- ные значения ее аргумента в достаточно ограниченном интервале – от 0,00 до 3,29. Поэтому авторами был разработан и численно реализован специальный алгоритм расчета значений функции ошибок для определения значений температуры океанической части литосферы.

Как известно, функция ошибок обычно пред- ставляется в виде следующего выражения:

ВЕСТНИК 2017

2x erf (x) — —^fexp(—t2)dt.                 (11)

A n o

Разлагая подынтегральное выражение в ряд Тейлора, получим:

,     2 =, (—1) n x ² n ^{+ 1}

erf ( x ) — —^> -— ----—

П n — o n !(2 n +1)

357 9

x x x x x--- + — — — + — x11

+ ^ I . (12)

^^^^^^B

3  10 42 216 1320

ⁿ V

Согласно признаку Д’Аламбера, ряд (12) сходится на всей комплексной плоскости.

Таким образом, используя (10) и разложение (12), можно представить пространственное распределение температурного поля океанической литосферы Земли, что в конечном итоге позволяет проводить исследования ее термического режима посредством вариации граничных условий и численных значений параметров, входящих в модель, и использовать полученные результаты для оценок и прогнозирования характеристик геодеформационных процессов и возникающих в этой среде геодинамических рисков [4; 5].