Моделирование термостимулированного газовыделения водорода из металла методом Монте-Карло

Одним из интересных методов моделирования является метод статистических испытаний (метод Монте-Карло), который используется в частности, при изучении кинетики адсорбции, десорбции, каталитических реакций на поверхности. Его применение в этой области способствовало пониманию фундаментальной роли фазовых переходов, связанных с процессом упорядочивания структуры поверхностного слоя [1-4]. Изучение термодесорбции актуально во многих отношениях. Такие исследования, например, позволяют наиболее прямым и простым способом получить термодесорбционный спектр, что имеет важное значение, как для развития моделей термодесорбции, так и для рассмотрения технологических процессов, протекающих в металлах и сплавах [5].

Экспериментальная часть

Эксперимент состоит в следующем [6]. В начальный момент времени при достаточно низкой температуре Т 0 =Т(0) в реакторе находится катализатор с монокристаллической поверхностью, содержащей адсорбированные частицы одного сорта. Поверхность начинают нагревать по линейному закону:

T(t) = T(0) + bt, (1) где b — скорость нагрева [К/сек].

При повышении температуры десорбирующие частицы откачиваются из реактора. По количеству откачанного газа определяется зависимость скорости десорбции от температуры поверхности (термодесорбционный спектр).

Относительная простота эксперимента и ценная информация, заключенная в термоспектрах (ТДС), объясняют значительный интерес к данной проблеме.

Объекты исследования

Образцы нержавеющих сталей изготавливались из листового материала методом электроискровой резки в виде прямоугольных пластинок размерами 25 x 5,0 x 2,0 мм. Поверхности образцов были механически отшлифованы и отполированы, после чего отожжены в вакуумной печи при температуре 500˚С в течение 1 ч с последующим охлаждением без нарушения вакуума.

На рис. 1 приведены спектры термостимулированного газовыделения (ТСГВ) водорода Н 2 из стали 12Х12М1БФР для различных времен электролитического насыщения. Представлены результаты по выходам только Н 2 . Видно, что через 6 ч насыщения в спектре появляется пик при температуре ~400˚С. При увеличении времени насыщения до 48 ч (кривая 4) возрастает интенсивность пика в области 400-500˚С (E b ~1,0-1,3 эВ/aтoм) и появляется второй пик при Т~900˚С (E b ~ 2,4–2,6 эВ/aтoм). При дальнейшем увеличении времени насыщения общая картина спектра и интегральная интенсивность спектров не изменяется (рис. 1). Происходят лишь взаимные колебания интенсивностей пиков, что, по-видимому, связано с погрешностями при изготовлении образцов.

Y,отн. едн.

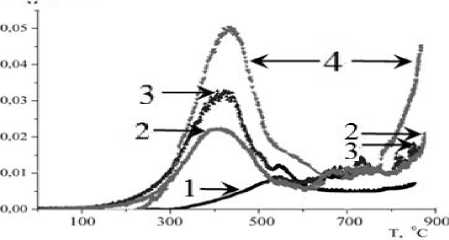
Рис. 1. Спектры ТСГВ водорода Н 2 из стали 12Х12М1БФР после разных времен насыщения: 1 – исходный образец; 2 – 6 ч., 3 – 24 ч., 4 – 48 ч. Плотность тока насыщения 0,2 А/см². Электролит 1М H 2 SO 4

Моделирование процесса термодесорбции

Для моделирования явления термодесорбции использовано несколько моделей различных уровней сложности и детализации ：

• 1.    МИАС (модель идеального адсорбционного слоя). Она не учитывает латеральных взаимодействий. Латеральное взаимодействие – взаимодействие атомов в соседних узлах решетки между собой.

• 2.    Модель с учетом латеральных взаимодействий.

• 3.    Модель с учетом латеральных взаимодействий и диффузии вещества на поверхности.

• 4.    Модель с учетом латеральных взаимодействий вещества без диффузии из объема. А только с диффузией на поверхности.

• 5.    Модель с учетом латеральных взаимодействий и диффузией вещества из объема и на поверхности.

Нами разработаны:

При каждой температуре подсчитывалось число молекул, покинувших поверхность, что и давало возможность построить имитационный спектр ТСГВ.

Результаты расчетов и их обсуждение

Единицы измерения некоторых величин представлены в табл. В моделе МИАС были заданы следующие условия [7]: поверхность размером 100х100 однородна; энергия десорбции 36 ккал/моль; отсутствует энергия отталкивания между соседями. Для модели МИАС мы получили один имитационный пик ТСГВ (рис. 2), вероятность десорбции для каждого узла одинакова. Этот результат соответствует решению дифференциального уравнения для термодесорбции.

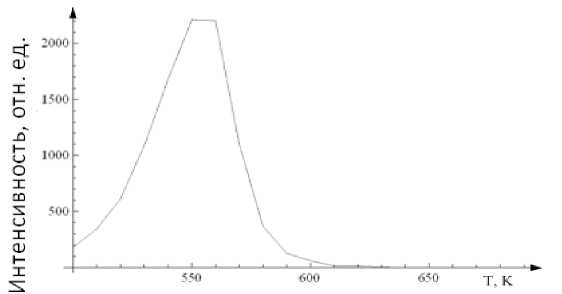
Рис. 2. Имитационный спектр ТСГВ в МИАС.

При включении в модель латерального отталкивания между ближними соседями, энергия латерального взаимодействия равна – 2 ккал/моль, между дальними соседями она не учитывается (остальные условия заданы те же, что и в МИАС), энергия активации десорбции начинает меняться в интервале

E a – 4 ε ≤ E a ≤ E a – 0 ε (2) где ε – энергия латеральных взаимодействий.

Таким образом, энергия активации десорбции меняется в зависимости от числа соседей десорбируемого атома. Поэтому появляются пять пиков, для энергии активации при 4, 3, 2, 1, 0 соседях (рис. 3).

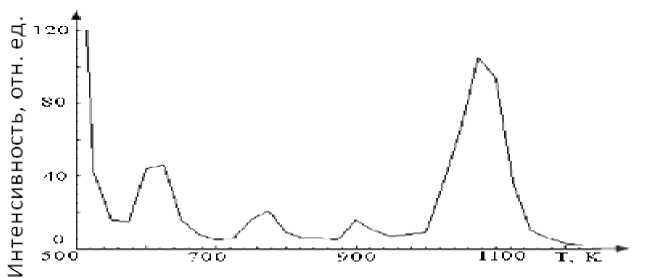
Рис. 3. Имитационный спектр ТСГВ с добавленным в модель латеральным взаимодействием

При добавлении в модель поверхностной диффузии, где энергия десорбции для всех центров 36 ккал/моль, латеральное взаимодействие равно – 2 ккал/моль и атомы стремятся занять энергетически выгодные узлы (узлы без соседей) и образуют устойчивую структуру С(2 х 2) (рис. 4).

Термодесорбционные пики при этом разделяются на два (рис. 5).

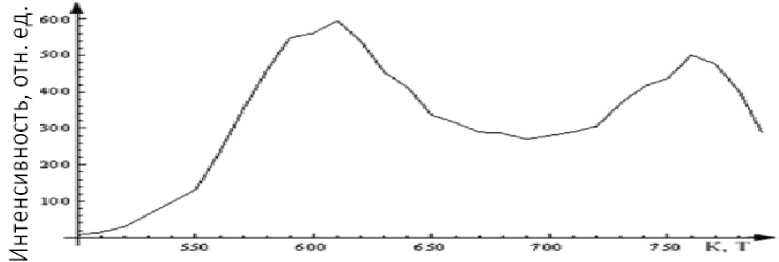
Рис. 5. Имитационный спектр ТСГВ с учетом латерального взаимодействия и диффузии на поверхности.

В четвертой трехмерной модели размер монокристалла равен 100х100х10, поверхность однородна, энергия десорбции для всех мест на поверхности 48 ккал/моль, энергия отталкивания между ближайшими соседями – 6 ккал/моль, скорость нагрева 10 К/с, начальное покрытие 1. В этой модели не происходит диффузии водорода из объема. Она протекает только на поверхности. Получен имитационный спектр ТСГВ с двумя пиками с их максимумами на 400К и 900К (рис. 6).

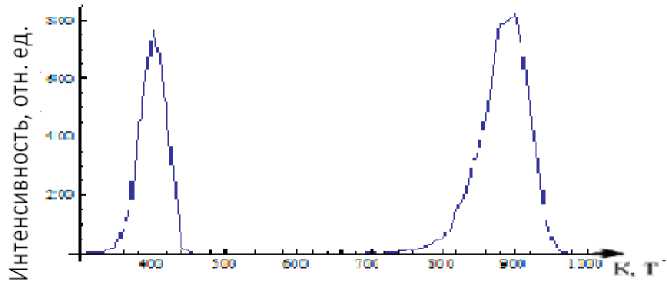
Рис. 6. Имитационный спектр ТСГВ в трехмерной модели с диффузией на поверхности

Первый пик связан с десорбцией молекул, имеющих по четыре ближних соседей. Затем идет область от 470 до 700К, когда десорбция отсутствует. Это область идеального порядка С(2х2) по всей решетке, возникает при заполнении поверхности меньше, чем на 1/2, при этом заполнении атомы занимают энергетически самые выгодные узлы (узлы без соседей). Она устойчива на протяжении интервала в 330 К, так как для диффузионного перескока (образования кластера из четырех соседей) частице необходимо преодолеть отталкивание 3 соседей (18 ккал/моль). С ростом температуры интенсивность диффузии возрастает, что приводит к разрушению структуры и случайному образованию кластеров различных размеров (от двух до четырех молекул). Ощутимая концентрация таких кластеров начинает образовываться при температуре 710К. С этой температуры начинается второй пик, уширенный и смещенный относительно последнего пика имитационного спектра.

В пятой модели (рис. 7), при включении в модель объемной диффузии форма пиков размывается, что связано с изменением ситуации на поверхности вследствие выхода вещества из объема. Имитационный спектр качественно совпадает с экспериментальными данными из рис. 2.

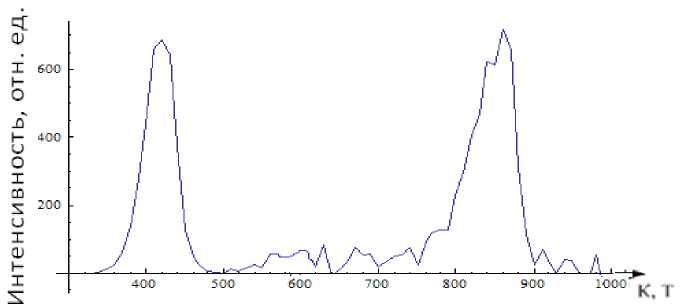
Рис. 7. Имитационный спектр ТСГВ в трехмерной модели с диффузией на поверхности и из объема.

Таблица

Характеристики моделей

Название модели	Энергия активации десорбции с поверхности			Энергия латерального взаимодействия (отталкивания) между соседями
	кэВ	ккал/моль	кДж/моль	кэВ	ккал/моль	кДж/моль
МИАС 1	1,56	36	150,84	-	-	-
Модель 2	1,56	36	150,84	0,09	2	8,38
Модель 3	1,56	36	150,84	0,09	2	8,38
Модель 4	2,08	48	201,12	0,26	6	25,14
Модель 5	2,08	48	201,12	0,26	6	25,14

Выводы

• 1.    Разработана имитационная модель термостимулированного газовыделения, которая учитывает механизм элементарных стадий на атомарном уровне – латеральные взаимодействия между атомами на поверхности и диффузию атомов из объема.

• 2.    Предложенная модель удовлетворительно описывает экспериментальные данные.