Моделирование трансформируемых механических систем
Автор: Ручкин Л.В., Ручкина Н.Л.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.18, 2017 года.
Бесплатный доступ
Приведены результаты моделирования трансформируемых механических систем, применяемых при создании робототехнических устройств и изделий космических аппаратов. Трансформируемые системы рассматри- ваются в виде многозвенных шарнирных механизмов с размещенными на звеньях или на основании приводами. Проведенный анализ публикаций показал, что при создании трансформируемых систем используются как разомкнутые, так и замкнутые кинематические цепи. Для описания работы использованы уравнения Лагранжа второго рода в матричной форме, которые спра- ведливы как для разомкнутых (последовательных), так и для замкнутых (параллельных) структур. С целью решения прямой задачи динамики и определения необходимых управляющих моментов приводов предложена математическая модель четырехзвенного механизма раскрытия штанги панелей солнечных батарей (после- довательная структура). При построении модели принято, что механизм работает в горизонтальной плоско- сти, моменты сил тяжести, приложенные к звеньям, воспринимаются устройствами обезвешивания. Моделирование проводилось в среде графического программирования LabVIEW, при этом разработаны виртуальные приборы, позволяющие вычислять координаты характерных точек механизма, например, цен- тров масс звеньев как точек крепления устройств обезвешивания, виртуальные приборы вычисления матриц инерции звеньев, кинетической энергии звеньев и необходимых моментов сил приводов. Предложенная модель и разработанные виртуальные приборы позволяют решать прямую задачу динамики трансформируемой механической системы и могут быть использованы при проектировании новых образцов робототехнических систем и изделий космических аппаратов.
Робототехника, многозвенный трансформируемый механизм, матричный метод, прямая задача динамики
Короткий адрес: https://sciup.org/148177766
IDR: 148177766 | УДК: 55.30.03;
Текст научной статьи Моделирование трансформируемых механических систем
Введение. При создании изделий ракетнокосмической техники, робототехнических и мехатронных устройств широко применяются различные трансформируемые механические системы (антенны, рефлекторы, манипуляторы и т. п.). Подобные системы можно рассматривать как многозвенные механизмы с размещенными на звеньях или основании приводами. Из-за сложности проектирования, изготовления и отладки, а также с учетом высокой стоимости подобных устройств возникает необходимость построения их математических моделей и определения динамических характеристик. В статье рассмотрено построение математической модели на примере четырехзвенного механизма раскрытия штанги панелей солнечных батарей [1–11].
Кинематическая модель. Четырехзвенный механизм, расчетная схема которого приведена на рис. 1, состоит из основания (звено 0) и трех шарнирно соединенных звеньев 1, 2 и 3. Шарниры расположены в точках A , B , F , оси шарниров параллельны между собой. Перемещения звеньев кинематически связаны при помощи тросовых передач. Привод звеньев размещен на основании.
Для описания указанного плоского многозвенного механизма, построенного по разомкнутой кинематической схеме с тремя вращательными ( В ) парами пятого класса, оси которых параллельны между собой, воспользуемся матричным методом, который применим для описания как замкнутых, так и разомкнутых кинематических цепей [12].
С каждой В парой связываем i-ю систему координат Хн, x2i, x3 i, где i = 0-2. Разметка осей приведена на расчетной схеме (рис. 1). Каждую ось x3,i направ- ляем вдоль оси соответствующего шарнира перпендикулярно плоскости чертежа, ось x1,i направляем вдоль или параллельно продольной оси i-го звена, ось x2i направляем так, чтобы система координат была правой.
Инерциальную систему координат x 10, Х 2 0, Х 3 0 связываем с основанием (звено 0). Переход от i- й к ( i – 1)-й системе координат описывается однородной матрицей перехода [12]
В инерциальной системе координат векторное уравнение кинематики четырехзвенного механизма имеет вид гi = °0 1 i-1 ■ г = В • гi r0 = A1 A2 Ai ri = Bi ri , где B = A ■ A2 ••• Ai-1, i = 1, 2, 3.
Механическая модель. Составим уравнение движения для четырехзвенного механизма. Для этого воспользуемся уравнениями Лагранжа второго рода, которые справедливы для описания как замкнутых, так и разомкнутых кинематических цепей.
Уравнения Лагранжа второго рода [2; 3] для плоского многозвенного механизма имеют вид d dL 6L „ ----= Mk, dt 5<7k dqk где k = 1, ...,n ; n - число степеней подвижности; L = K - P - функция Лагранжа; K - кинетическая энергия; P - потенциальная энергия; 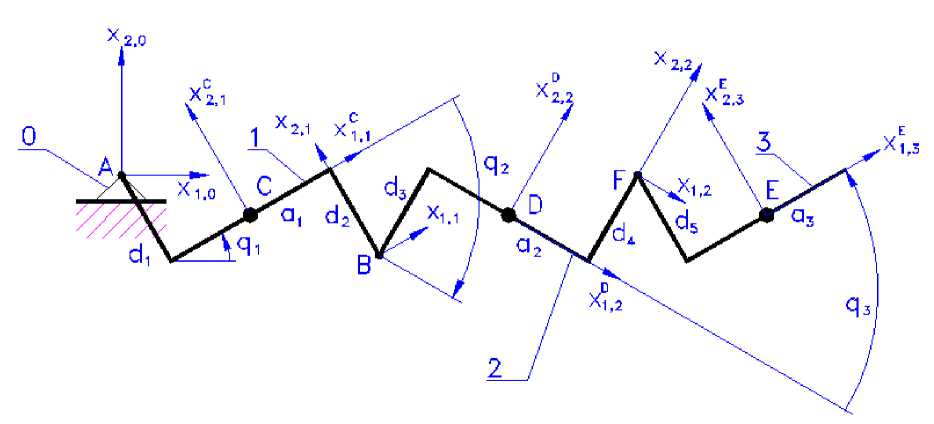
Рис. 1. Расчетная схема
Fig. 1. The design scheme
Полная кинетическая энергия i-го звена определяется [13; 14] выражением ii
K = f H Tr ( B i ■ Ii-B p ) • j 9 p ,
2 j = 1 p = 1
Rj 5 B.
где матрица B- = —i- описывает изменение матрицы a qj
Bi при изменении обобщенной координаты qj ; Ii – матрица инерции i -го звена; Т – знак операции транспонирования матриц.
Для сборки уравнений движения необходимо вычислить производные кинетической энергии по обобщенным скоростям и времени.
Для звеньев механизма
K = Tr ( B ^ ■ 1 1 ■ B ^T ) ■ q i , a q i 7 '
Kb- = Tr ( B 2 ■ 1 2 ■ B 2 T ) ■ <1 1 + Tr ( B 2 ■ 1 2 ■ B 2T ) ■ fc,
K = Tr(B^ ■ 13 ■ B3T )■ <11 + aq 3 V )
+ Tr ( b 3 ■ 1 3 ■ b 3 T ) ■ q 2 + Tr ( b 3 ■ 1 3 ■ b 3 T ) ■ q 3.
Матрица A10C преобразования системы координат — C — C — C x1,1 , x2,1 , x3,1 к инерциальной системе координат
X 1 0 , x 2 ° , x 3 ° имеет вид
0 qd A 1C = A 1 A 2 C .
Матрица A 2 1 D преобразования системы координат X 1 2 D , x 2 2 D , x 3 2 D , связанной с центром масс звена 2 (точка D ), к системе координат x 12, x2 2, x 32, начало которой располагается на оси шарнира В , имеет вид 1 q 2
A2 D = A2 A2 D , где A2q – матрица поворота.
Определим необходимые матрицы преобразований для звена 3 механизма.
Матрица A 3 q элементарного поворота на угол q 3
|
вокруг оси x 3,3 |
имеет вид |
|
|
cos q 3 - sin q 3 O O |
||
|
Aq |
= |
sin q 3 cos q 3 O O |
|
3 |
O O 1 O |
|
|
_ O O O 1 _ |
||
Матрица A 3 3 E элементарных сдвигов от системы
— — — координат x1,3 , x2,3 , x3,3 , связанной с центром масс звена 3 (точка E), к системе координат Х1 2, x2 2, x3 2, начало которой располагается на оси шарнира F, имеет вид
|
1 |
0 |
0 |
a 3 2 |
|
|
3 A 3 E = |
O |
1 |
0 |
— d |
|
° |
0 |
1 |
0 |
|
|
L ° |
0 |
0 |
1 |
Матрица A 3 2 E преобразования системы координат
— E — E — E — — — x1,3 , x2,3 , x3,3 к системе координат x1,2 , x2,2 , x3,2
имеет вид
2 q 3 A 3 E = A 3 A 3 E .
Определим [13; 14] матрицы Bijk , описывающие изменение матриц Bij при изменении координаты qk :
в11 = IB1=^( D ■ Ac )=D2 ■ Ac=D2 ■ Aq ■ A2c , a q1 a q1 v 7
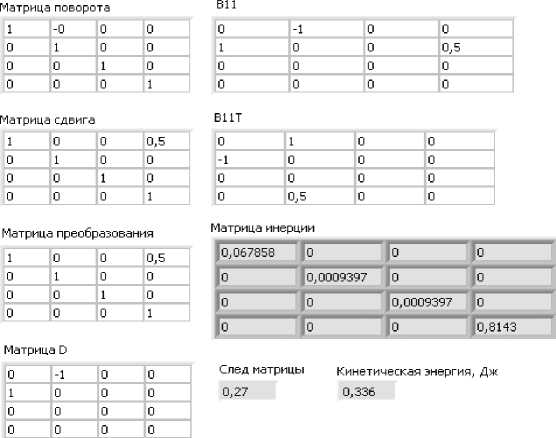
B'12 =3^ = R(D- B222 = 5^ = /A0 ■ D ■ A1 А A0 ■ D2 ■ A1 212D 12D dq 2 в? - IB1 = ^ (D ■ A10 ■ A2 -A2e ) = D ■ A0 ■ A2. ■ D ■ A3E, aq 2 aq 3 v 7 B? - IB2 = ^ (AO ■ D ■ A2. ■ A3e ) = A10 ■ D ■ A2. ■ D ■ a3e , aq 2 aq 3 v7 B3 = IB2=^ (AO ■ A2 ■ D ■ A2e )=A1O ■ A2 ■ D2 ■ a2e , aq 2 aq 3 v7 где для вращательных пар матрица D имеет вид "O -1 O O" D = 1 0 0 °.0 0 0 0 ° ° ° ° Уравнение движения для k-го звена имеет вид i=k ^ Tr (BRlrBf ) qj + j=1 i=k + £ Tr (BiP^i -BfT)-qj qp = Mk. j, p=1 Механизм работает в горизонтальной плоскости, моменты сил тяжести, приложенные к звеньям, воспринимаются устройствами обезвешивания. Моментами сил трения в шарнирах на первом этапе исследования можно пренебречь. Следовательно, в качестве обобщенной силы принимаем момент сил М1, приложенный к звену 1. Звенья кинематически связаны и для полного раскрытия q2 =-2■ q1, q3 = 2 q1. Моделирование проводилось в среде графического программирования LabVIEW [15; 16]. Задав диапазон изменения обобщенной координаты q1, решаем прямую задачу кинематики, график изменения координат центров масс звеньев приведен на рис. 2. Для решения прямой задачи динамики созданы виртуальные приборы (ВП), позволяющие вычислять матрицы инерции звеньев, кинетическую энергию звеньев и необходимые усилия или моменты сил приводов (рис. 3). а - длина звена R2 - внешний радиус Рис. 2. Графики изменения координат центров масс звеньев механизма Fig. 2. Graphs of the change in the coordinates of the centers of mass of the links of the mechanism q - угол поворота звена., град О dl-сдвиг по оси XI, м 0,5 0,05 d2-CABMr по оси Х2, Рис. 3. Лицевая панель ВП вычисления кинетической энергии первого звена Fig. 3. Front panel of the VP of calculating the kinetic energy of the first link Заключение. В результате выполненной работы разработаны математическая модель и виртуальные приборы, позволяющие решать прямую задачу кинематики и динамики трансформируемых механических систем, т. е. на основании заданных законов движения и массоинерционных характеристик звеньев определять необходимые обобщенные силы или моменты, развиваемые приводами звеньев. Результаты исследования могут быть использованы при проектировании робототехнических и мехатронных систем, а также при разработке механических систем космических аппаратов.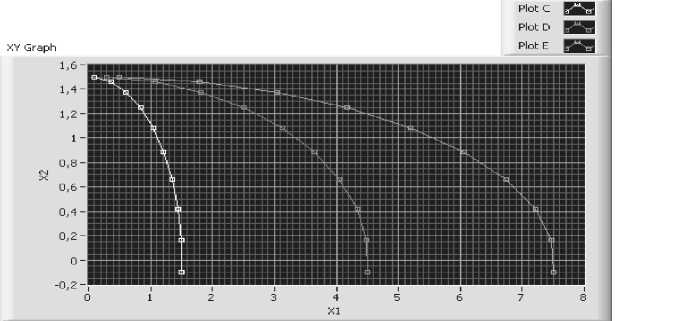

Список литературы Моделирование трансформируемых механических систем
- Ручкин Л. В., Крючков М. А. Исследование движения манипулятора, построенного по замкнутой кинематической схеме ВВВВВВ с параллельными осями//Автоматизация и моделирование в производстве приборов: межвуз. сб. науч. тр. М.: МИП, 1989. C. 82-88.
- Ручкин Л. В. Моделирование манипулятора с параллельным расположением приводов//Спутниковые системы связи и навигации: тр. Междунар. науч.-техн. конф. (30 сент. -3 окт. 1997 г.) В 4 т. Т. 2/КГТУ. Красноярск, 1997. С. 21-26.
- Ручкин Л. В. Графическое моделирование плоских манипуляторов//Математические модели и методы их исследования: тезисы докладов/Краснояр. гос. ун-т. 1999. С. 177-178.
- Система обезвешивания изделий космического аппарата на базе манипуляторов/Н. Л. Ручкина //Решетневские чтения: материалы XII Междунар. науч. конф., посвящ. памяти генер. конструктора ракет.-космич. систем акад. М. Ф. Решетнева (10-12 нояб. 2008, г. Красноярск)/под общ. ред. И. В. Ковалева; Сиб. гос. аэрокосмич. ун-т. Красноярск, 2008. С. 26.
- Ручкин Л. В., Ручкина Н. Л. Компенсация сил трения в механизмах устройств имитации невесомости//Лесной и химический комплексы -проблемы и решения: сб. ст. по материалам Всерос. науч.-практ. конф. (9 дек. 2016 г.). Т. 1/СибГАУ. Красноярск, 2016. С. 146-153.
- Ручкин Л. В., Ручкина Н. Л. Силовой расчет параллельного манипулятора в программном пакете LabVIEW//Решетневские чтения: материалы XXI Междунар. науч.-практ. конф., посвящ. памяти генер. конструктора ракет.-космич. систем акад. М. Ф. Решет-нева (08-11 нояб. 2017, г. Красноярск). В 2 ч. Ч. 1/под общ. ред. Ю. Ю. Логинова; Сиб. гос. аэрокосмич. ун-т. Красноярск, 2017. С. 527-528.
- Корендясев А. И., Саламандра Б. Л., Тывес Л. И. Теоретические основы робототехники/отв. ред. С. М. Каплунов; Ин-т машиноведения им. А. А. Благонравова РАН. В 2 кн. Кн. 1. М.: Наука, 2006. 383 с.
- J.-P. Merlet. Parallel Robots. Springer, 2006. 418 p.
- Буянкин В. М. Управление электроприводами для механизмов параллельной кинематики робота манипулятора типа «Хобот»//Исследование наукограда. 2012. № 1. С. 29-36.
- Эффективные методы решения задач кинематики и динамики робота-станка параллельной структуры/Л. А. Рыбак . М., 2011. 148 с.
- Подзоров П. В., Бушуев В. В. Синтез структур технологического оборудования на основе механизмов параллельной кинематики//Мехатроника, автоматизация, управление. 2002. № 4. С. 11-18.
- Фу К. С., Гонсалес Р. К., Ли К. С. Робототехника: пер. с англ. М.: Мир, 1989. 624 с.
- Динамика управления роботами/В. В. Козлов . М.: Наука. Главная редакция физико-математической литературы, 1984. 384 с.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. Главная редакция физико-математической литературы, 1984. 832 с.
- Суранов А. Я. LabVIEW 7: справочник по функциям. М.: ДМК Пресс, 2005. 512 с.
- Автоматизация физических исследований и эксперимента: компьютерные измерения и виртуальные приборы на основе LabVIEW 7/под. ред. П. А. Бутырина. М.: ДМК Пресс, 2005. 264 с.


