Моделирование ударного сжатия и теплового расширения пяти металлов

В настоящее время в литературе описано большое количество уравнений состояния веществ (УРС) от очень простых до очень сложных [1-3]. При изучении поведения сплошных сред, которые подвергаются воздействию динамических нагрузок, применяется математическое моделирование, выполняющееся на электронных вычислительных машинах (ЭВМ). Число компонентов в сложных моделях многокомпонентных сред с химическими реакциями и фазовыми переходами может достигать нескольких десятков, а то и сотен. При расчете смеси в таких моделях затраты машинного времени могут растягиваться на значительное время даже с использованием современных ЭВМ. Предлагаемый малопараметрический УРС значительно сократит время расчета на ЭВМ сложных физических процессов.

Уравнения на поверхности сильного разрыва

В случае идеальной среды (девиатор тензора напряжений равен нулю и отсутствует теплопроводность) законы сохранения массы, импульса и энергии на поверхности сильного разрыва (ударной волны) имеют вид р-(D-U) = ро ■(D-Uо),(1)

р.( d - и) и - р = ро ■( d - ио) ио - Ро,(2)

Ро = о.(3)

В уравнениях (1)-(3) величины без индекса характеризуют состояние за разрывом, D - скорость ударной волны. Величины с индексом, такие как р _о - плотность, U _о - массовая скорость, Р _о - давление, E _о - удельная внутренняя энергия, описывают состояние вещества перед разрывом. Рассмотрим ударную волну в покоящемся веществе. Согласно [1] уравнение состояния рассматривалось в предположении, что величины Р _о и E _о пренебрежимо малы по сравнению с Р и E . Уравнения (1)-(3) принимают вид при Р _о = о, E _о = о и U _о = о :

р ■ ( D - U ) - р о D = о, р о DU = Р ,                         (4)

E = ¹ DU ■ 1 1 - ^р I .                                 (5)

2 I р )

Система, состоящая из трех уравнений, (4), (5) содержит пять величин P , р , E , U , D. Если любые две из них получены экспериментальным путем, то остальные величины можно найти из выражений (4) и (5). Точка на ударной адиабате определяется полностью. Зависимость между экспериментально измеренными D и U известна уже более пятидесяти лет и описывается линейным соотношением

D = С 0 + b • U .                                    (6)

На основе большого количества обработанных экспериментальных данных в справочнике [2] содержится информация по D ( U ) соотношениям.

Давление P определяется калорическим уравнением состояния (УРС) вида P = P ( р , E ) в том случае, если р и E - независимые термодинамические переменные. Сложные и трудоемкие современные УРС рассмотрены в [3], [4], однако, для экспресс-расчетов достаточно использовать простые УРС.

В [1] рассмотрено уравнение состояния вида

P = Рх (р) + Pt (р, 5), E = Ex (р) + Et (р, 5),                    (7)

где

Р х =— ( х " n — 1 ) , P t = р о C 2 • f ( 5 ) • х ^Y , n

EX = C-f х^ +  n -1), ET = Cf) XV,.

n — 1 ^ n n J          у — 1

C ₀ - скорость звука перед ударной волной при P = P ₀, р = р ₀, 5 - энтропия,

Y = const, х = р ₀/ р .

Зависимости P_X ( E X , х ) и P T ( E T , х ) следуют из (8) и (9)

_ ^{( n —} 1 ) ^р 0 E X      2 f ^{1 —} X )       _ _⁽ Y ^— 1 ) р о ^E T

^Р х =----- X -----^{+ р} 0 C 0 • ( _х J ,      ^P T =----- X-----’

УРС получим путем подстановки (10) в (7), которое принимает следующий вид

P = ( Y — 1) ро Eх 1 + ф(х), n = const,

где

^{ф ( х} ) = (n п ^х ( n — 1 ) n

n^ Y—1 Y

+ 7------\---.

( n — 1) х n

Согласно [1] уравнение (11) называется «уравнением с согласованными у и n », если у = n . Таким образом, уравнение (11) примет вид

P = ( n — 1) р0 E • х

^{1 + р} о ^C о ( ^{х 1 —} 1 ) ,

где р ₀, С о и n - постоянные величины.

Далее рассмотрим, при каких условиях уравнения (4), (5), (12) согласуются с линейной зависимостью D ( U ) . Зависимость D ( U ) получим, путем исключения P , E и х в выражениях (4), (5) и (12).

n + 1

D = nT U + г 2 +1 — U

.

Сравнивая выражение (13) с выражением (6), можно увидеть, что эти зависимости различа-n + 1 Т Т ются. Наименьшие отличия находятся в области 4 U ^ С0 .

Так как предположение о постоянстве n в УРС (12) приводит к нелинейной зависимости D ( U ) в выражении (13), которая, в свою очередь, не согласуется с линейной зависимостью D ( U ) (6), сделаем наоборот. Линейную зависимость D ( U ) (6) примем за основу, P и E выра-

Математика

зим через C0 и b из выражений (4) - (6). Полученные выражения подставим в (11) и найдем уравнение в котором n вдоль ударной адиабаты не может быть постоянной величиной n = 2 b •( 2 - b-(1 - x ))-1,                                     (14)

Уравнение состояния

Поведение вещества вместо УРС (12) будем описывать уравнением, в котором справедливо предположение, что n не зависит от x

P = ( n ( x ) ^- 1 ) ^- р оK x ^{- 1} E + р о k c 02k • ^ф ( x ) .                            ⁽¹5)

В уравнении (15) р _0K , C 0 _K - плотность и скорость звука в точке P = 0, T = 0 , x = 1.

В [5-7] использовалось УРС типа (15), где величина n зависит от x . В уравнении (14) величина n линейно зависит от x в том диапазоне D и U , в котором справедлива зависимость D ( U ) (6). Из выражений (4), (5) и (15) следует зависимость n ( x ) (14), именуемая далее экспериментальной.

Функция n(x) должна иметь максимум в окрестности x «1 согласно [2] и [3]. Таким образом, если x = 0 и n = n0, то справедливо утверждение, что nm > n0. Будем использовать простую функцию вида ax2

ⁿ ( ^x ) = ⁿ 0 ⁺ ( n m ^{- n} 0 )--------------- "У ,                            ⁽¹⁶⁾

2      2     2 ²

ax ⁺ ( X ^- x m )

где a =

16 x m ²       _.

^{4 -} ( n m ^{- n} 0 ) ²

Зная, что при x = 0 и x = ^ n ( x ) = n ₀ , а также при x = x m

n ( x ) = n m , из (16) найдем произ

водную n ( x ) в виде

dn dx

( n m ^{- n} 0 ) • ^{2 ax 2} ( x m - ^{x 2} )

I 2        2      2 2 I

I ax ⁺ ( ^{x -} x m ) I

Производная n ( x ) равна нулю при x = 0 , x = ^ и x = x_m . То есть, с большой долей достоверности вещество можно считать газом с у = n ₀ при бесконечно большом сжатии x » 0 и бесконечно большом разрежении. Значение n ₀, как и значения n_m , x_m , подберем из условия наилучшего описания экспериментальных данных, т.к. область применимости малопараметрического УРС ограничена конечным сжатием.

Функцию ф ( x ) из (15) возьмем в виде, максимально близком к выражению (12)

Ф ( x ) = x + •                                          (18)

Разделим давление и энергию на холодные и тепловые составляющие для определения температуры и теплоемкости:

P = P x ( x ) + P t ( x , T ) , E = E x ( x ) + E t ( x , T ) .                        (19)

В соответствии с [7] зависимость E_T ( x , T ) возьмем в виде

AT ²

T 0(x) + T ’ где A - индивидуальная характеристика вещества, для простых веществ близкая к 3R/р; R -универсальная газовая постоянная; р - молекулярная масса. Дифференцируя выражение (20), получим теплоемкость при постоянном x

_ AT •(20(x) + T)

.

CV =            А

( 0 ( x ) + T )

В соответствии с [7] выражение для теплового давления будет иметь вид

РТ =

A d 0 ( x )     T ²

---

•

0 ( x ) dx    0 ( x ) + Т

Зная, что справедливо уравнение

Pt =(n(x) — 1)SSK-Et , x получим характеристическую функцию 0(x), которая связана с n(x) уравнением

d In 0( x)    n (x) — 1

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B               ^^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

^^^^^^^в

.

dx         x

Зависимость 0 ( x ) следует из выражений (24) и (16)

Г k

x + B • xm

0(x) = 00 • x1—n0 •

x + —• x

m

k B 7

,

R 2 + ( nm где B = -—-— 2 — ( nm

^^^^^^^в

^^^^^^^в

ⁿ 0 )

n 0 ) "

Дополнительно, сделаем такое условие, чтобы изобара Р = 10

■—‘

4 ГПа проходила через точку,

характеризующую нормальное состояние ( Р = 10

. —‘

⁴ ГПа, Т = 293 °К, р = р ₀ , С_Р = С_{Р 0} ), а также

через точку плавления при Р = 10

—

⁴ ГПа ( Т = Т_пл , С_Р = С_Рпл , р = р _пл ). При описании зависимо -

сти С_Р ( Т ) при Р = const следует выразить С_Р через Т и x . С этой целью воспользуемся уравнением из [8]

C p = C v

^^^^^^^в

t\ k d T 7 X

Г dP k

р0 к " I       I

k dx 7 t

.

Г dРу k                                                       Г d P k

Зная, что I — I = 0 продифференцируем выражение (23). Производная I I запишется kd T 7 x                                                   kd T 7 x в виде

dPT k =( n (x) — 1)' р0 к

d T 7 x

x

• C v .

Так как выражение (19) справедливо, то производная

dP k = dPx +

dP k

— I будет иметь вид d x 7 _T

dP k

d x 7 _T   dx k d x 7 _T

.

Уравнение состояния вещества определяется совокупностью уравнений (15)-(17) и (25) и содержит 7 параметров: р0к , С0к, A, n0, nm, xm и 00 . Численные значения этих параметров определяются таким образом, чтобы наилучшим образом описать поведение ударной адиабаты со- стояния вещества в точке, характеризующей нормальное состояние Р0 = 10

—

⁴ ГПа, Т ₀ = 293 °К,

P 0 = p ( ^P 0 , ^T 0 ) , C P 0 = C P ( P 0 , ^T 0 ) ^{и в точке плавления Р} пл = ^{10 4 ГПа}, ^Т 1 = ^Т пл , Р 1 = Р пл ( ^Т пл , ^Р 0 ) ,

С р 1 = С р ( Т пл , Р о ) ■

Математика

Результаты расчетов

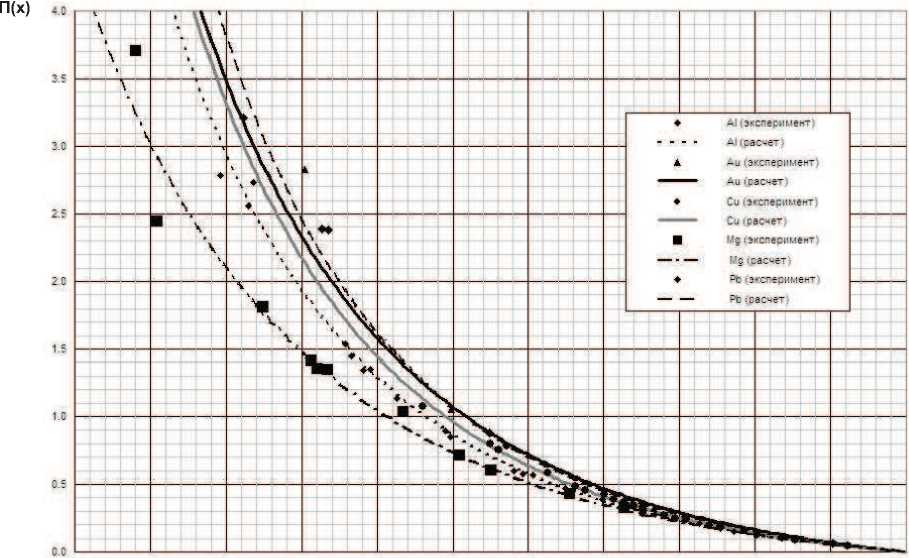
Расчеты выполнены для нескольких простых веществ - металлов. При помощи оригинальной версии симплекс-метода выполнен подбор основных параметров уравнения состояния. В качестве целевой функции выбрана сумма квадратичных разностей между расчетными и эксперимен тальными значениями теплового расширения вещества и теплоемкости при постоянном давлении. Для рассмотренных материалов получено удовлетворительное совпадение с экспериментальными данными. На рис. 1 показано сравнение безразмерного давления для ударных адиабат рассчитываемых материалов. Величина безразмерного давления определяется по формуле (29):

Π= ^P ₂. ρ ₀ C ₀

В качестве сравниваемых величин давлений используются экспериментальные, взятые из [2], и теоретические, определяемые из выражения (15).

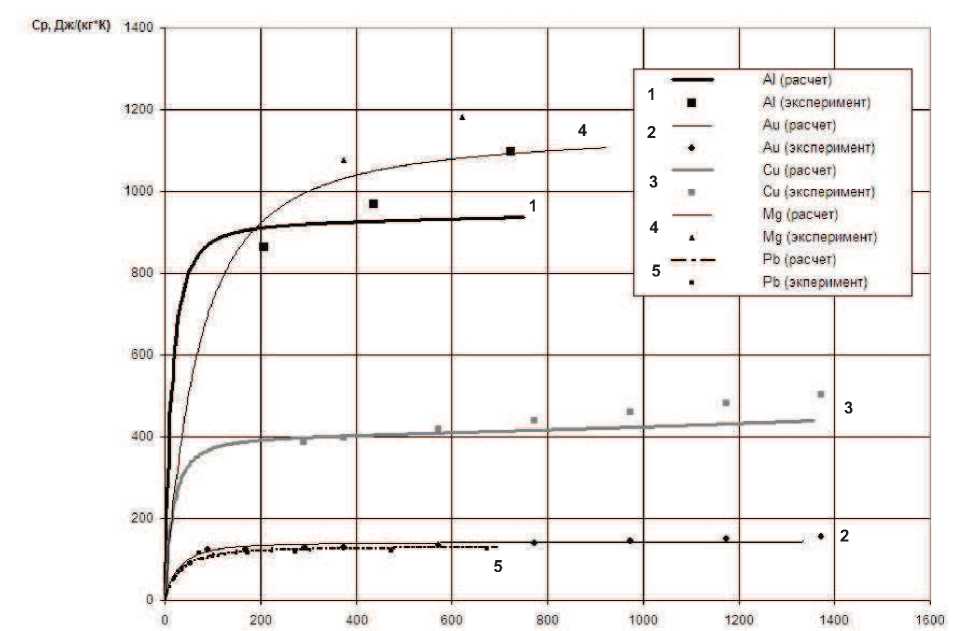
Зависимость теплоемкости от температуры приведена на рис. 2, экспериментальные значения теплоемкости взяты из справочника [9]. В таблицу сведены результаты расчетов подбора основных параметров УРС.

045          0.5          0 55          06          0.65          07          0.75          0.8          0.85          0.9          0.95           1

x

Рис. 1. Сравнение экспериментальных и теоретических зависимостей П(х) на ударной адиабате

Результаты подбора основных параметров уравнения состояния

Величины	Вещества
	Al (алюминий)	Au (золото)	Mg (магний)	Pb (свинец)	Cu (медь)
n 0	1,62	1,515	1,291	1,719	1,49
nm	1,933	2,564	1,944	2,027	2,997
xm	1,908	2,485	2,613	1,66	2,484
Р ок , г/см 3	2,908	19,668	1,833	11,501	9,014
C 0 K , км/с	5,642	3,402	4,724	2,102	3,904
A - 10 6 , кДж/г	920,39	140,65	1106,14	127,6	394,94
^ 0 , К	15,012	8,004	43,141	39,198	1,466

Температура. К

Рис. 2. Сравнение экспериментальных и теоретических зависимостей Ср ( 7 )