Моделирование влияния деформации изгиба в одномодовом оптическом волокне на показатель преломления сердечник - оболочка

Резкий рост информатизации, приобретающий глобальный характер, требует увеличения скорости и способов доступа к получению информации, что, в свою очередь, зависит от разработки новых или модернизации действующих телекоммуникационных линий связи [1–3]. В настоящий момент высокоскоростными являются волоконно-оптические линии связи [3], где наибольшую скорость передачи обеспечивают одномодовые оптические волокна [3; 4]. Однако резкое увеличение скорости передачи информации даже в подобных сетях невозможно. Это связано с ограничениями вследствие уширения длительности бит, вызванного различной скоростью распространения составляющих импульсов светового излучения.

Для дальнейшего увеличения скорости передачи информации необходимо учитывать, во-первых, внешние факторы влияния среды [1; 2], в которую помещается волокно в процессе эксплуатации: механические вибрации, температуру [2–4], давление и влажность окружающей среды, различного вида деформации [4–8], электромагнитное поле [2], во-вторых, физические свойства самого одномодового оптического волокна. В реальных опти-

Моделирование влияния деформации изгиба в одномодовом оптическом волокне ...

Резак Елена Владимировна аспирант, старший преподаватель кафедры программного обеспечения вычислительной техники и автоматизированных систем, Тихоокеанский государственный университет, город Хабаровск. Сфера научных интересов: математическое моделирование физических процессов, проектирование и разработка программно-информационных систем. Автор более 40 опубликованных научных работ. SPIN-код: 1778-5510, AuthorID: 595857.

ческих волокнах из-за нарушения круговой симметрии возникает небольшая анизотропия, поэтому, с учетом того, что световая энергия распределена между состояниями поляризации, различие констант распространения вызывает увеличение длительности импульса на выходе оптического волокна. И те и другие факторы оказывают влияние на затухание сигнала в оптическом волокне [1–4], на изменение показателя преломления оптического волокна, что препятствует дальнейшему увеличению скорости передачи информации [1–4].

Анизотропия оптического волокна может быть связана либо с нарушением идеальной круговой формы сердцевины [1; 3; 5], либо с наведенным двулучепреломлением вещества [2; 4], например, из-за несимметричных напряжений в материале [1–5; 9] оптического волокна, либо из-за несовпадения геометрических центров сердцевины и оболочки [5].

Различные авторы разделяют факторы роста анизотропии профиля волокна на две группы.

Первая группа объединяет статические факторы: несовершенство заводского процесса вытяжки волокон [1–4]; скрутка волокон при изготовлении волоконно-оптического кабеля [1–3; 5]; изгибы оптического кабеля и, как следствие, механические деформации волокон, возникающие в процессе укладки кабеля [4; 5].

Вторая группа – динамические факторы: вариации внешних факторов окружающей среды (внешнего электромагнитного поля, излучения, температуры, колебаний и др.) – для волоконных кабелей, проложенных в грунт [1–5]; динамические деформации волокон (ветровые нагрузки, вариации температуры окружающей среды, деформации вследствие оледенения кабеля) – для подвесных линий связи [1; 4].

В силу специфичности отрасли связи (большая протяженность линий, малые поперечные размеры оптических волокон, высокая стоимость материалов и работ по прокладке кабеля, усложняющих процесс исследования в реальных условиях) необходимо проводить предварительное моделирование для упрощения изучения влияния различных факторов на потери сигнала в волокне.

Нерешенность некоторых задач, связанных с поведением сигнала на изгибе линии связи, позволяет говорить о необходимости исследования влияния деформации, в частности деформации изгиба, на оптическое волокно и сигнал, проходящий по такому волокну [1–5; 9].

Модель деформации оптического волокна

Ниже предложена модель деформации изгиба оптического волокна (Рисунок 1). На модели показаны: диаметр оболочки оптического волокна (примем его значение равным 2 b , что связано с расположением оси волокна в начале координат); радиус изгиба волокна R ; ϕ – угол изгиба волокна.

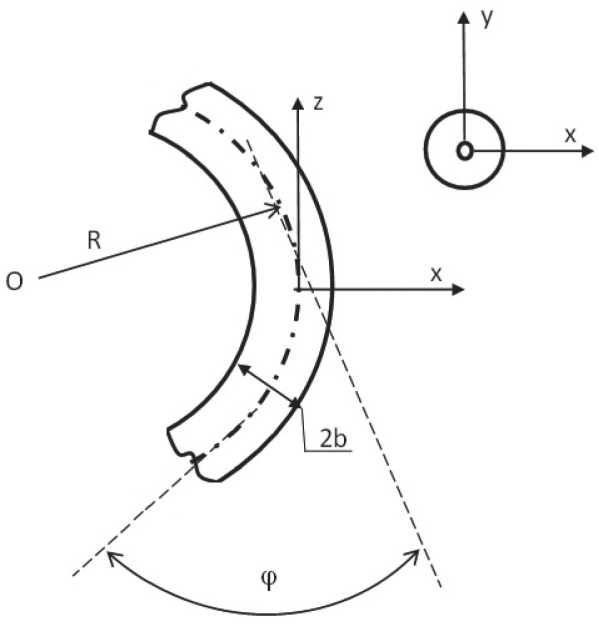
Рисунок 1. Модель изгиба одномодового оптического волокна Источник: здесь и далее рисунки и схемы выполнены автором.

Деформация рассматривается в направлении осей Х , Y , и Z . Однако необходимо отметить, что изменения, вносимые деформацией изгиба, будут вноситься составляющими в направлении осей Х и Z, так как значения по оси Y в результате изгиба в пределах сердечника изменяться не будут.

Математическая модель деформационных составляющих волокна

Согласно [5; 9; 10] составляющие механического напряжения в изогнутом волокне выражаются как

° x = 2 К ^{2 (} x ² b 2 ) , ^a y = 0,

E

°z = Kx, где E – модуль Юнга; x – координата относительно центральной оси волокна.

С учетом эффекта Пуассона составляющие относительных деформаций имеют следующий вид:

^S x = i a - ^V° y + ° z ) ]

• y = = i l_ ^ y ^- ^ ( ^a x ^{+ c} z ) ] ,                             ⁽²⁾

Z = = | [ ^ Z ^- a ( ^ x ⁺ a y ) ]

где ц - отношение Пуассона.

Подставляя (1) в (2), получим составляющие относительных деформаций для изогнутого волокна:

Моделирование влияния деформации изгиба в одномодовом оптическом волокне ...

£ x

—R (x2 - b2)

M --x

R

\^e y

- M -Ц- (x ² - b ² ) +— X

L 2 R ^2V        ’ R

^г — ^x z R

- 2 M ( x ² - b ² )

Необходимо отметить, что в системе (3) учтены все составляющие относительных деформаций и эффекта фотоупругости в направлениях координатных осей с использованием коэффициентов Поккельса, в отличие от классической теории, в которой не рассматриваются значения x << b [2; 4; 5; 10]. Отсутствие квадратичных составляющих приводит к потере полной картины, происходящей в оптическом волокне под воздействием деформации изгиба.

Рассмотрим изменение показателя преломления, вносимое различными составляющими относительных деформаций (3) и эффектом фотоупругости в направлениях координатных осей 5 n_x , 5 n_y и S nz с использованием коэффициентов Поккельса pjj .

5 nx —	2 ( p 11 ^ x + p12£ y + p12£ z )
5 ny —	n 3 2""( p12£ x + p11£ y + p12£ z )
6 nz —	n 3 2""( p 12e x + p12£ y + p11£ z )

Подставим (3) в (4) и найдем изменение показателя преломления, а затем его значение в направлении координатных осей:

3 n nx = n ⁺Т

(5а)

n

y

p

⁺ P 12 ^- ^12 ^M

L₊ M I P n_ „ k 2 ।^{x +} R ² 1 2 M p ¹² ) b ,

n ³

—n+T

M I P I M /

T?! P 11 ^{- 222 +} P 12 I x +- ( ² P 11 +

R ² (      M ) R

^{2 p} 12 I , ^M I ^p 12               I 2

+2 p 12         Ix + 2I       p12 p11 Ib m )   R21 m         )

n ³

n₇ — n +-- z 4

^M I _     ^p 12 , „ I 2^ ^M.

_2 I p 11       ⁺ p 12 I ^{x +} _D ^{( 4} p 12

R ² V      M ) ^R

—

^{2 p} 11 L , ^M I ^p 12 ---- I x +—-I ---

M )    R ² V M

^- P 12 ^- P 11 | ^b b

(5b)

На основании формул (5а)–(5в) с помощью программной среды MathCad был произ- веден расчет составляющих показателя преломления с использованием значений коэффициентов Поккельса и Пуассона из [2; 4; 5; 11]:

• •    P ii = 0.121 ;

• •    p i2 = 0.270 ;

• •    ц = 0.164 .

Диаметр волокна 2 = 125 мкм, значения показателей преломления сердечника n = 1,4738 и оболочки n _об = 1,4627 для длины волны ЛЯМБ=1310 нм взяты для оптического волокна типа TrueWave с ненулевой смещенной дисперсией при радиусе искривления оптического волокна R = 2 мм.

Полученные результаты отображены на Рисунке 2. Здесь х – координата относительно центральной оси одномодового оптического волокна; n – значение показателя преломления сердечника неизогнутого волокна; n _x, n _y, n _z – значения показателя преломления изогнутого волокна в направлении координатных осей внутри сердечника. Точками 1 и 2 обозначены переходы изогнутого оптического волокна из двухосного состояния кристалла в одноосное.

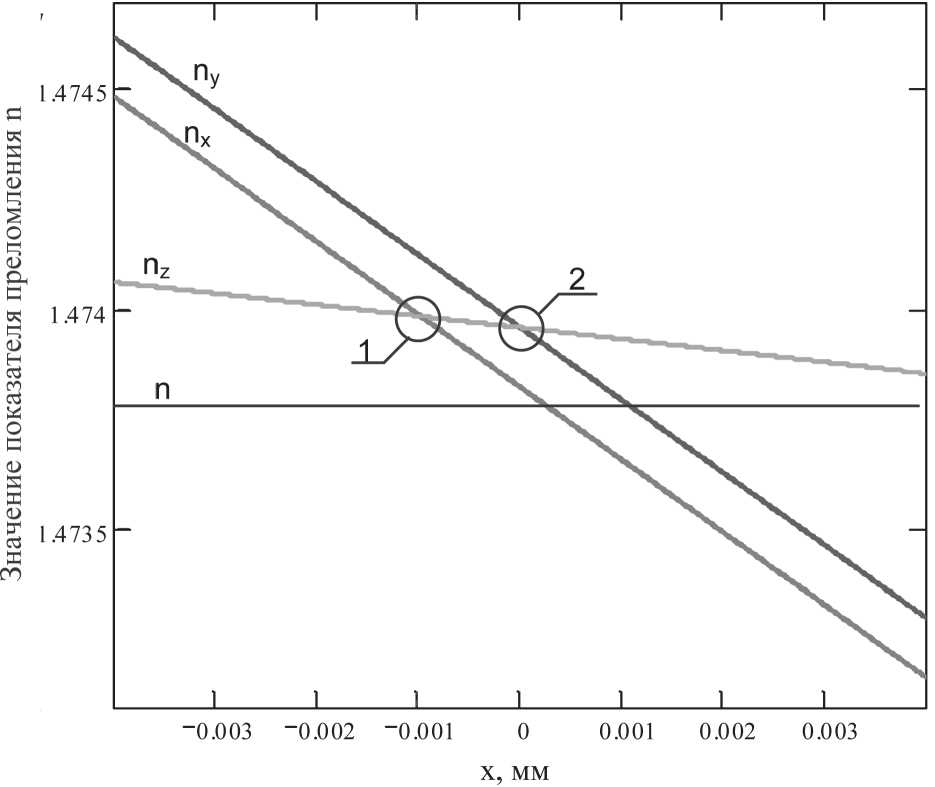
Рисунок 2. Изменение показателей преломления изогнутого волокна внутри сердечника в направлении координатных осей

На Рисунке 2 видны изменения значений показателей преломления в зависимости от изменения значения координаты x , при этом значения n _x, n _y и их разности не зависят от других координат.

Согласно полученной математической модели, результаты которой представлены на Рисунке 2, распространение излучения в изогнутом волокне происходит так же, как вну-

Моделирование влияния деформации изгиба в одномодовом оптическом волокне ...

три двухосного кристалла. При этом существуют два таких взаимных расположения n _x, n _y и n _z (точки 1 и 2 на Рисунке 2), при которых n _x = n _z и n _y = n _z; таким образом, в данных точках свет распространяется по деформированному волокну как по одноосному кристаллу.

Заключение

После изучения параметров изогнутого оптического волокна, математической модели влияния деформации изгиба на одномодовое оптическое волокно и полученных теоретических результатов можно сделать следующие выводы.

Показатели преломления для всех трех взаимно перпендикулярных направлений неодинаковы:

• •    при изгибе оптического волокна распространение света в нем происходит так же, как по двухосному анизотропному кристаллу;

• •    в случаях при x ₁ = 0 и и x ₂ = –1 мкм распространение света по изогнутому волокну происходит так же, как по одноосному кристаллу;

• •    на оси оптического волокна ( x ₁ = 0) значения показателя преломления изогнутого оптического волокна отличаются от показателя преломления недеформированного оптического волокна, что приводит к сдвигу максимума поля моды;

• •    значения показателя преломления оптического волокна при изгибе и до него будут смещены n = n _x относительно оптической оси, то есть на оптической оси показатель преломления при изгибе будет больше начального.

Поскольку в одномодовом оптическом волокне существует продольная составляющая электрического поля, изгиб оказывает существенное влияние на электродинамику, причем данное влияние оказывается необратимым, так как значение n _z в пределах сердечника волокна оказывается больше показателя преломления сердечника до изгиба.