Моделирование влияния формы кровеносного капилляра на фильтрационно-реабсорбционные процессы

Обмен веществ между кровью и клетками ткани происходит на уровне микроциркуляторного русла, где жидкость и растворенные в ней вещества, а также частично макромолекулы переходят сквозь полупроницаемую стенку кровеносного капилляра в интерстициальное пространство, где происходит обмен веществ с клетками ткани. После чего жидкость частично всасывается обратно в кровеносное русло, частично – в лимфатические капилляры.

Среди многообразных механизмов переноса жидкости и макромолекул через полупроницаемую мембрану сосудистой стенки наибольшего внимания заслуживают фильтрация (вызывается гидростатическим градиентом давлений внутри и вне сосуда), диффузия (обеспечивается концентрационным градиентом давлений) и везикулярный транспорт (поддерживается физиологической активностью клеточных структур) [7, 8]. Последний механизм в данной работе не рассматривается.

Первым исследователем, предположившим, что переход жидкости из крови в межклеточное пространство обусловлен не только фильтрацией, но и диффузией, был Э. Старлинг [5]. Согласно его гипотезе объемная скорость движения жидкости через капиллярную стенку J определяется соотношением гидростатического и коллоидноосмотического давления в капилляре и межклеточной жидкости:

J = C ^{[( Р} ГК ^{— Р} ГТ ^{)- (} P OK ^- P OT ^)] , ⁽¹⁾ где P_ГК – гидростатическое давление в капилляре, P_ГТ – гидростатическое давление в тканевой жидкости, P_ОТ – онкотическое давление тканевой жидкости, P_ОК – онкотическое давление плазмы в капилляре, C – коэффициент гидравлической

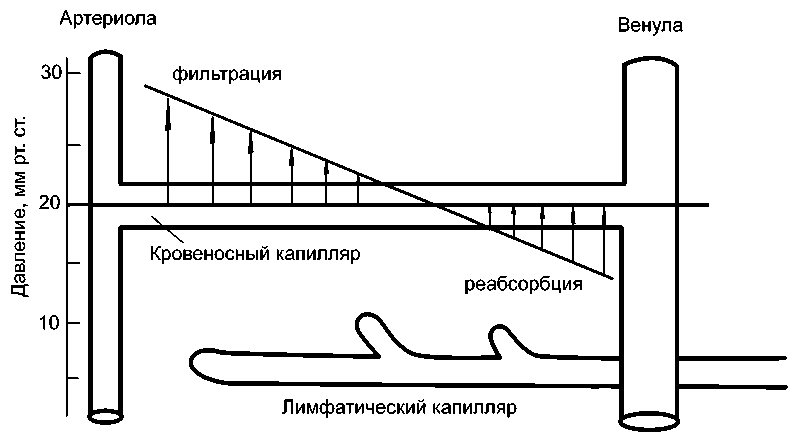
Рис. 1. Схема типичного капилляра, иллюстрирующая фильтрационно-реабсорбционную гипотезу Старлинга [5]

проницаемости капиллярной стенки. Данное уравнение носит название закона Старлинга. Когда величина J положительна, происходит фильтрация жидкости из капилляра, когда отрицательна – жидкость переходит из межклеточного пространства в капилляры – происходит реабсорбция.

По предположению Старлинга в межклеточном пространстве гидростатическое давление P_ГТ и онкотическое давление P_ОТ одинаковы. Поэтому он считал, что на артериальном конце капилляра, где велико гидростатическое давление, происходит фильтрация жидкости из сосуда, а на венозном – гидростатическое давление падает и в результате происходит реабсорбция (рис. 1). В некоторой точке капилляра отсутствует как фильтрация, так и реабсорбция, поскольку здесь давления, вызывающие фильтрацию и реабсорбцию, равны. Кроме того, Старлинг полагал, что в нормальных условиях фильтрация жидкости несколько превышает ее реабсорбцию, так что часть жидкости остается в межклеточном пространстве, откуда впоследствии поступает в лимфатическую систему.

Следует отметить, что гипотеза Старлинга была подтверждена экспериментами [4, 5] и до сих пор является основой представлений о транскапиллярном обмене веществ.

Математическая модель фильтрационно-реабсорбционных процессов в кровеносном капилляре

Рассмотрим математическую модель процессов, происходящих в микроциркуляторном русле. Данные процессы можно разделить на три этапа: движение жидкости в кровеносном капилляре параллельно с ее фильтрацией и реабсорбцией в межклеточное пространство; движение жидкости в межклеточном пространстве; абсорбция и движение в лимфатическом капилляре [8].

Будем рассматривать течение плазмы крови, которую можно считать ньютоновской (линейно-вязкой) жидкостью. Влияние форменных элементов крови (эритроцитов, лимфоцитов и т.д.) не учитывается. Течение считается ламинарным и стационарным. Кровеносный капилляр моделируется жесткой трубкой с порами в стенке.

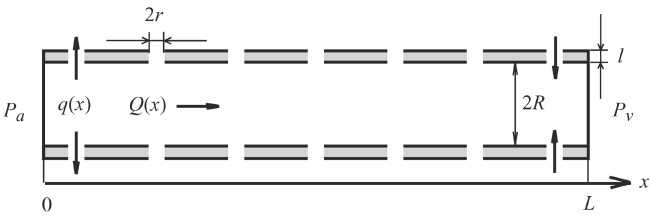
Рис. 2. Модель кровеносного капилляра: r – радиус поры в стенке капилляра, R – радиус капилляра, L – его длина, l – толщина стенки, P_a – давление на артериальном конце, P_v – на венозном, Q ( x ) – объемная скорость течения жидкости вдоль капилляра, q ( x ) – объемная скорость течения жидкости через все поры на поверхности капилляра единичной длины [6]

Проанализируем течение жидкости в кровеносном капилляре. Рассмотрим два одновременно протекающих процесса: движение жидкости вдоль капилляра и поперек через поры в его стенке (рис. 2). Для описания течения вдоль капилляра используется закон Пуазейля, для описания движения жидкости через поры в стенке капилляра – закон Старлинга. Такой подход описан в работе [6].

Перейдем к построению модели. Объемная скорость течения воды через поры равна уменьшению объемной скорости ее течения по капилляру на длине dx :

dQ ( x ) = - q ( x ) dx .

По закону Пуазейля для "продольного" течения по капилляру

Q(x) = - 1 dP(x) W dx

.

Величина P ( x ) = P_ГК ( x ) - P_ГТ – результирующее гидростатическое давление (разность между гидростатическим давлением в капилляре и ткани). При этом считается, что гидростатическое давление в ткани неизменно. Удельное гидравлическое сопротивление капилляра единичной длины имеет вид:

W = ^{8 η} ,

π R ⁴

где η – коэффициент вязкости жидкости.

Для «поперечного» течения через поры в стенке капилляра применим закон Старлинга:

_{q ( x ) =} P ( x ) - P o _, w

где результирующее онкотическое давление P_o = P_ОК - P_ОТ считается постоянным.

Величина

8 η l         4 η l

w=        =

πr4N2πR π2r4NR представляет собой гидравлическое сопротивление всех пор на поверхности капилляра единичной длины. Обозначая λ = w и подставляя (3) и (4) в (2), получим W дифференциальное уравнение второго порядка:

d 2P(x) P(x)

-     =- dx 2      λ2

Решение данного уравнения имеет вид:

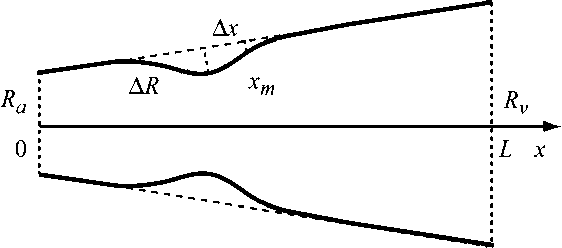
Рис. 3. Схематическое изображение конического капилляра с локальным сужением xx

—    --

P ( x ) = Ae ^х + Be ^х + P o .

Коэффициенты A и B определяются из граничных условий на величины гидростатического давления на артериальном (x = 0) и венозном (x = L) концах капилляра:

P (0) = P a , P ( L ) = P v .

Описанная выше модель хорошо известна и применяется в учебной литературе для качественного описания обменных процессов, происходящих в идеализированном кровеносном капилляре. Далее рассмотрим несколько усовершенствований данной модели, позволяющих учесть некоторые особенности реальных капилляров.

Реальные капилляры часто имеют вид конических трубочек, обычно расширяющихся к венозному концу [7,8]. Радиус пор также непостоянен и увеличивается к венозному концу капилляра [7, 8].

Первым усовершенствованием модели является учет изменяющегося радиуса пор в стенке капилляра. Был рассмотрен случай линейного изменения радиуса пор. В этом случае радиус зависит от продольной координаты по формуле:

r ( x ) = M x + r a , (8)

где ra и rv - радиус пор на артериальном и венозном концах капилляра, соответственно. В этом случае коэффициенты w и λ будут зависеть от x , и уравнение (5) не будет иметь очевидного аналитического решения. Поэтому в этом и последующих случаях решение граничной задачи осуществлялось численно с помощью метода отложенных поправок [2].

Рассмотрим теперь случай конического капилляра (рис. 3). Радиус капилляра считается линейно зависящим от x :

R -R

R ( x ) = R a + л , (9)

где R a и R v - радиусы капилляра на артериальном и венозном концах. В этом случае гидравлическое сопротивление капилляра W также будет зависеть от продольной координаты x .

Для капилляра с измененной геометрией объемная скорость течения жидкости через поры в его стенке направлена по нормали к стенке в данной точке и считается пропорциональной разности результирующих давлений в капилляре и ткани в этом направлении. Таким образом, и для капилляра с сужением считается справедливым уравнение (4).

Еще один интересный случай - локальные изменения радиуса капилляра, например, отложения на стенках капилляра (рис. 3). Зависимость радиуса от продольной координаты задавалась в следующем виде:

R ( x ) = R a + R v   R a x - ae bx ^{+ cx} 2 ,

x m 2 x                   1

где a =-AR • e^{2 A x} , b = —- и c =---. Здесь A R - максимальная величина

A x ²          2 A x ²

сужения, x m - координата центра сужения (точка максимального сужения), A x -расстояние от точки перегиба функции y = ae^{bx + cx} 2 до центра сужения - характеризует протяженность сужения (рис. 3).

Результаты

На рис. 4 представлены зависимости от координаты x давления (а) и объемной скорости продольного (б) течения, полученные с помощью описанной модели для цилиндрического капилляра с постоянным радиусом пор. Для небольшого радиуса пор графики давления показывают хорошее соответствие с результатами, предсказанными Старлингом, и экспериментальными данными [3, 4]. При больших радиусах пор проявляется нелинейность изменения гемодинамических параметров вдоль капилляра.

При увеличении радиуса пор область равновесия становится более протяженной. Тот же эффект получается при увеличении количества пор в стенке капилляра.

На рис. 5 представлено изменение распределения давления при повышении артериального или венозного давления. Видно, что эти изменения приводят к нарушению равновесия: фильтрация преобладает над реабсорбцией и в ткани остается избыточная жидкость. Тот же эффект достигается при уменьшении результирующего онкотического давления. Данные результаты согласуются с экспериментальными данными [3, 4]. Избыточная жидкость, остающаяся в ткани при превышении фильтрации над реабсорбцией, поступает в лимфатический капилляр.

Ситуация, когда реабсорбция преобладает над фильтрацией, возникает либо при уменьшении артериального или венозного давления, либо при увеличении результирующего онкотического давления.

На рис. 6 представлен профиль давления при линейно увеличивающемся радиусе пор в стенке капилляра. Видно, что он совмещает в себе черты графиков для малого (ближе к артериальному концу) и большого (ближе к венозному концу) радиуса пор. Сначала давление понижается почти линейно, но на этапе реабсорбции линейный характер распределения нарушается. Кроме того, фильтрация будет превышать реабсорбцию тем больше, чем сильнее увеличивается радиус пор в стенке капилляра.

Профили давления для конического капилляра показаны на рис. 7. В этом случае даже для небольшого радиуса пор наблюдается нелинейное распределение давления по длине капилляра. Расширение капилляра к венозному концу приводит к более быстрому падению давления в капилляре и, как следствие, к увеличению участка реабсорбции. При этом преобладание реабсорбции над фильтрацией увеличивается с увеличением угла раствора а .

Рис. 8 показывает распределение давления для конического капилляра с увеличивающимся радиусом пор. Видно, что увеличивающийся радиус пор несколько компенсирует преобладание реабсорбции, вызванное увеличением радиуса капилляра.

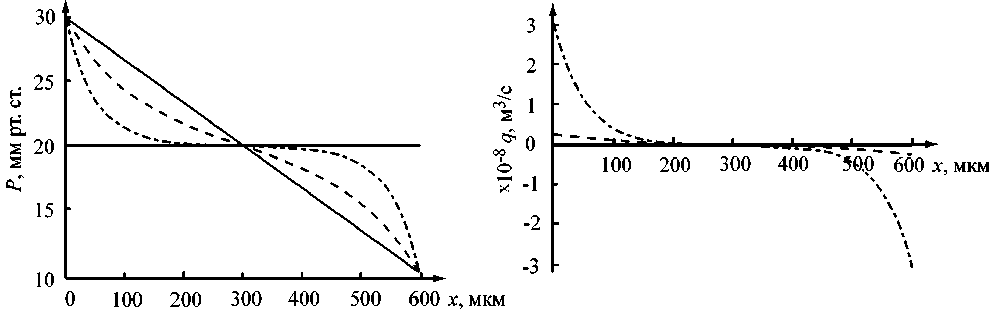
а

б

Рис. 4. Распределение гемодинамических величин вдоль кровеносного капилляра для различных радиусов пор: r = 20 нм (сплошная линия), r = 100 нм (пунктирная линия), r = 200 нм (штрих-пунктирная линия). Расчетные данные: P a = 30 мм рт.ст., P v = 10 мм рт.ст., P o = 20 мм рт.ст., R = 3,5 мкм, l = 0,9 мкм, п = 0,001 Па^с, N = 1,5 • 10¹² 1/м² [6, 7]

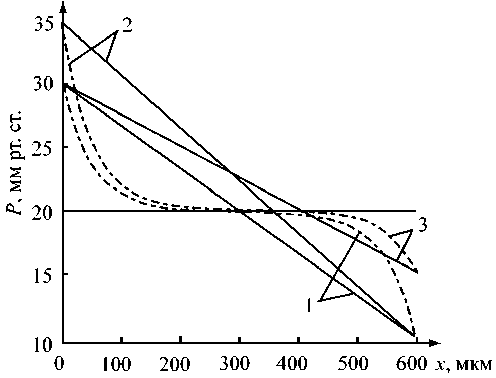
Рис. 5. Влияние повышения венозного давления P v = 15 мм рт.ст. (2) и артериального давления P a = 35 мм рт.ст. (3) на распределение гемодинамических величин вдоль кровеносного капилляра для различных радиусов пор: r = 20 нм (сплошная линия), r = 200 нм (штрих-пунктирная линия). 1 - распределение в норме: P a = 30 мм рт.ст., P v = 10 мм рт.ст., P_o = 20 мм рт.ст.

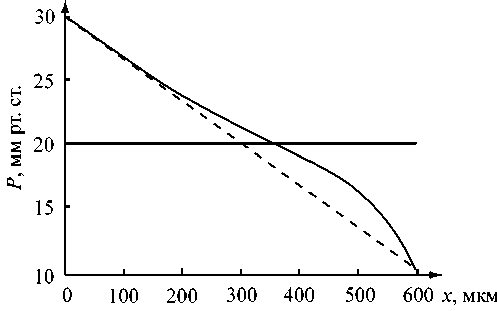
Рис. 6. Влияние линейного увеличения радиуса пор в капилляре: r a = 50 нм, r v = 150 нм (сплошная линия), r = const = 50 нм (пунктирная линия)

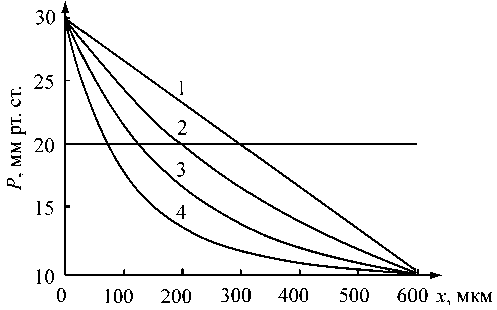
Рис. 7. Распределение давления в коническом капилляре с различным углом раствора: R_a = 3,5 мкм, R _v = 3,5 мкм (1), R_v = 5 мкм (2), R_v = 7 мкм (3), R_v = 10,5 мкм (4)

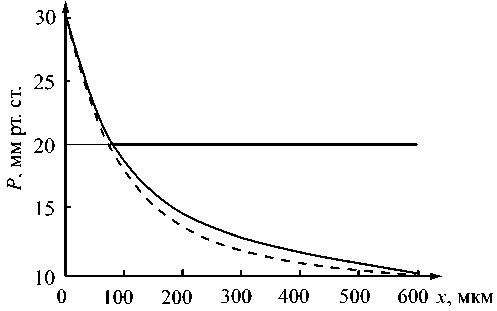
Рис. 8. Распределение давления в коническом капилляре с увеличивающимся радиусом пор: R_a = 3,5 мкм, R_v = 10,5 мкм, r_a = 50 нм, r_v = 150 нм (сплошная линия); r = const = 50 нм (пунктирная линия)

На рис. 9 представлены профили давления для конического сосуда с локальным сужением. Наличие дефекта, как и следовало ожидать, сильно изменяет характер распределения давления. Сужение капилляра приводит к увеличению давления в районе начала дефекта, вызывая как следствие усиление фильтрации. Затем, в наиболее узкой части капилляра, происходит падение давления, величина которого тем больше, чем более выражен дефект. В результате давление опускается до величины меньшей, чем давление в соответствующей точке нормального конического капилляра, что приводит к усилению реабсорбции на оставшемся участке капилляра. Таким образом, наличие сужения капилляра приводит к усилению как фильтрационных, так и реабсорбционных процессов и существенно влияет на обмен жидкости между капилляром и тканью.

Изменение профиля давления для капилляра с дефектом зависит от расположения, величины и протяженности этого дефекта (рис. 9). Чем больше величина и протяженность дефекта, тем сильнее он влияет на фильтрационно-реабсорбционные процессы в капилляре. Расположение сужения у артериального конца капилляра изменяет распределение давления практически на всей длине капилляра (рис. 9б). Если же дефект расположен у венозного конца, то на значительной части капилляра существенных изменений давления не наблюдается (рис. 9а).

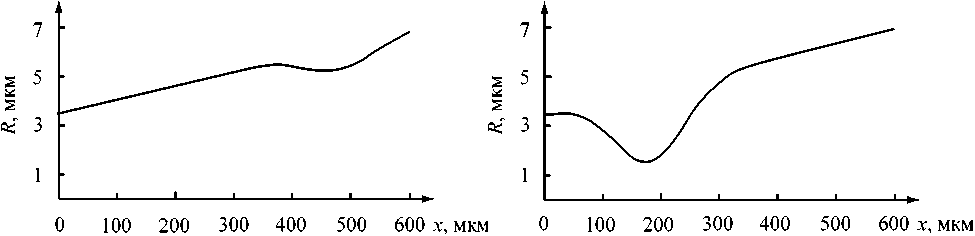
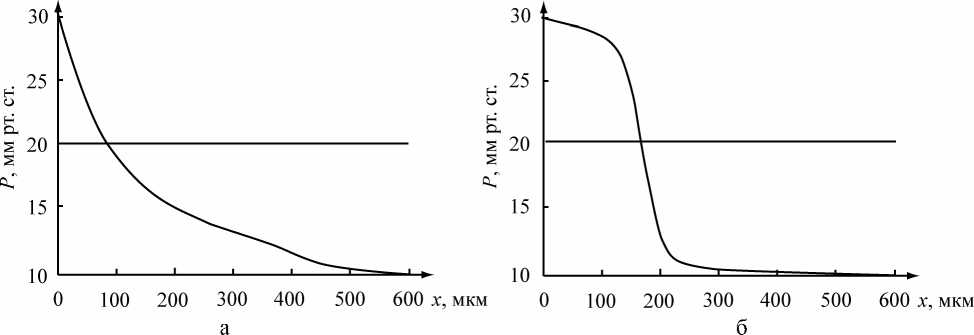
Рис. 9. Зависимость радиуса капилляра от координаты и распределение давления в коническом капилляре с локальным сужением стенок: (а) слабый дефект у венозного конца: R ( x ) = 3,5 + 0,583 - 10 2 x - 0,127 - 10 ^{- 13} e ^{0,133 x - 0} , ^{139 - 10 x} мкм,       A R = 1 мкм,       x m = 480 мкм,

A x = 60 мкм; (б) сильный дефект у артериального конца капилляра: A R = 3 мкм, x m = 180 мкм, A x = 60 мкм, R ( x ) = 3,5 + 0,583 - 10 ² x - 0,033 e^{0,050 x - 0} , ^{139 - 10 x} мкм

Выводы

В работе рассмотрена простейшая модель фильтрации и реабсорбции жидкости в кровеносном капилляре. Эта модель позволяет качественно оценить зависимость гидростатического давления, объемной скорости течения жидкости вдоль капилляра и сквозь поры в его стенке от продольной координаты. Представлен ряд усовершенствований известной модели, позволяющие учитывать геометрию реального кровеносного капилляра и особенности его строения. Полученные зависимости качественно совпадают с данными экспериментальных наблюдений [3, 4] и результатами, полученными с помощью других моделей [1].