Моделирование влияния оснастки на конечную форму изделий из полимерного композита

За последние десятилетия произошел существенный рост использования полимерных композиционных материалов (ПКМ) при изготовлении ответственных силовых конструкций в авиастроении, космической технике и гражданской сфере. Пропорционально ему увеличился и объем научных исследований, направленных на изучение технологических процессов, применяемых при создании композиционных материалов (КМ). Главной целью при этом является снижение производственных дефектов и поиск оптимальных технологий изготовления КМ, выгодных экономически и технологически. Комплексный анализ механических моделей, описывающих различные стадии современных процессов получения

композитных конструкций с термореактивной матрицей, предпринят в [1], где рассмотрены некоторые модели процессов пропитки сухой преформы, пултрузии профилей и отверждения композита.

Одна из важнейших тем современных исследований — это моделирование отверждения изделия при высокой температуре. Широко наблюдаемым на практике остаточным эффектом является искажение формы конструкции, обусловленное процессами, сопровождающими отверждение связующего: его химической усадкой во время полимеризации и температурной усадкой при охлаждении до комнатной температуры.

Остаточные напряжения, возникшие в результате отверждения, могут быть настолько велики, что способны вызвать разрушение в матрице еще до приложения нагрузки [2]. Их величина растет с увеличением толщины ламината [3]. В некоторых случаях значительные напряжения фиксируются еще до охлаждения изделия [4, 5]. Показано, что они зависят от температуры, при которой происходит гелирование связующего [6]. На ранних этапах научного поиска для аналитического вычисления остаточных напряжений была предложена модель, описанная в [7].

В толстых ламинатах отмечается сильная зависимость искаженной формы изделия от параметров процесса отверждения [3]. Авторами [8] изучены эффекты температурного цикла. Влияние скорости охлаждения рассмотрено в работах [9, 10]. На данный момент экспериментально прослежена зависимость изменения внутреннего угла детали типа «уголок» от многих параметров, таких как начальная величина угла, толщина ламината, укладка, поверхность оснастки, цикл отверждения [11–13]. Авторы [14] продемонстрировали, как воздействуют давление в автоклаве и скорость охлаждения на деформированную форму тонких ламинатов с асимметричной выкладкой. В статье [15] объяснены механизмы, отвечающие за изменение угла изделия типа «уголок» при отверждении. Авторами [12] классифицированы и экспериментально изучены различные механизмы искажения формы ламината. Отмечено, что влияние химической усадки матрицы при этом значительно [6, 15].

Существует обширный список работ по термомеханическому поведению термореактивных полимеров и композитов на их основе в условиях релаксационных и фазовых переходов [16–20]. Исследование отверждения конкретного связующего проведено в [21]. Множество авторов опираются в своих работах на уравнение кинетики полимеризации в форме Аррениуса [7, 22, 23]. В [24] прослежена эволюция механических и деформационных свойств материала при полимеризации. Часто свойства материала слоя, зависящие от параметров процесса, получают осреднением [25–27].

Упругие определяющие соотношения, в которых модуль Юнга связующего меняется в процессе отверждения кусочно-линейно, рассмотрены в [25, 26]. Модель, учитывающая релаксацию напряжений при обратном фазовом переходе, построена в [22] и применена в [28] для нахождения технологических деформаций. Данные подходы сравнивались авторами работы [29].

Вязкоупругие модели [9, 30–32] используются многими авторами, но недостаток этих моделей заключается в необходимости знать большое число параметров материала. Соответствующие свойства связующего изучались в работах [6, 21]. Авторами [26, 33] приводятся процедуры представления вязкоупругих определяющих соотношений в приращениях.

В большинстве публикаций моделируется композит, состоящий из слоев с однонаправленными волокнами, однако существуют работы, посвященные и текстильным композитам [34, 35]. В настоящее время разработанные модели годятся как для тонких [2, 5], так и для толстых ламинатов [30, 35]. Авторами [32] рассматривались композиционные цилиндры, произведенные намоткой на металлическую основу. Показано, что для таких конструкций упругая модель дает чрезмерное завышение остаточных напряжений, поэтому должны учитываться эффекты вязкоупругости. В работах [23, 36] исследовался участок панели, подкрепленной стрингером. Авторы экспериментальных работ [29, 37] измеряли остаточные деформации в ламинате с помощью оптоволоконных датчиков.

В работе [28] моделирование отверждения позволило продемонстрировать влияние технологических деформаций на величину нагрузки, при которой в композите начинается расслоение. В [38] аналогичная механическая модель описывала деформации, приобретаемые изделием в процессе пултрузии.

Авторы [39] применили двухмерный анализ отверждения, но трехмерный анализ деформирования и таким образом уменьшили вычислительные затраты. В статье [10] для тех же целей была использована комбинированная конечно-элементная сетка, состоящая из оболочечных элементов в плоских областях и твердотельных — в местах скруглений.

В работе [12] перечислены факторы, сказывающиеся на искажении формы изделий из композита. Одним из них является взаимодействие изделия с технологической оснасткой. В процессе отверждения композита она придает требуемую форму конструкции и принимает участие в процессе теплопереноса. Кроме того, оснастка, вследствие эффекта теплового расширения, оказывает механическое воздействие на конструкцию на этапе изготовления. В статье [5] отмечено, что тип оснастки (внутренняя или внешняя) вносит вклад в величину искажения формы изделия. Авторы [13] показали, что условие на границе контакта является важным. Вопросы взаимодействия изделия с оснасткой также изучались в [8]. В [29] сделан вывод о том, что для адекватного представления нужна схема контакта с учетом проскальзывания и прилипания.

В данной работе с помощью численного моделирования рассматривается влияние материала оснастки на конечную форму изделия, приобретаемую им в процессе отверждения. Предложена модель контакта, учитывающая переход от проскальзывания к прилипанию в момент гелирования связующего. Выявлены и проанализированы различные виды нарушений геометрии исследуемой конструкции и продемонстрирована их связь с величиной коэффициента теплового расширения (КТР) материала оснастки.

2.    Описание моделей отверждения

В то время как армирующие волокна сохраняют свои свойства в процессе отверждения, изначально жидкое связующее в результате проходящей полимеризации последовательно сменяет несколько состояний. Его первая значительная трансформация — это гелирование: полимер превращается из жидкого в высокоэластичный твердый материал, проявляющий вязкоупругие свойства и способный нести малые нагрузки. В ходе полимеризации также растет температура стеклования связующего. В момент, когда ее значение превышает температуру в изделии, происходит второе изменение свойств полимера, связанное с переходом в стеклообразное состояние, которое характеризуется значительным повышением упругого модуля матрицы.

Процесс отверждения композита в каждой точке среды можно описать монотонно возрастающей функцией X(t), называемой степенью полимеризации связующего в текущий момент времени. Значение X = 0 соответствует неполимеризованному связующему, а значение X = 1 — полностью полимеризованному. Зависимость X(t) является решением дифференциального уравнения dX/dt = f (X, T, t), называемого уравнением кинетики полимеризации. В нем через T обозначена температура в рассматриваемой точке пространства в текущий момент времени, а через t — время от начала процесса отверждения. Конкретная запись этого соотношения выбрана здесь как уравнение Аррениуса:

dX/dt = Ae- E ^{( RT} ) ( 1 - X ) n X a ,                                     (1)

где A , n , a — параметры, R — универсальная газовая постоянная.

Распределение температур в сплошной среде находится из решения уравнения теплопроводности:

p(d( cT)/dt) = - div q + q , где p — плотность, c — удельная теплоемкость материала, q — удельная мощность тепловыделения. Вектор потока тепла q связан с градиентом температуры законом Фурье

• q, = - kj (a ту ax),

в правую часть выражения для которого входят компоненты тензора теплопроводности k_ij .

В процессе отверждения вследствие химической реакции, протекающей в связующем, происходит выработка тепла пропорционально скорости полимеризации. Для чистого связующего удельная мощность тепловыделения определяется по формуле:

q = p mHм (dX/dt), где pm — плотность связующего, а Hto, — удельная теплота, отвечающая полной полимеризации. Для осредненного материала принято считать, что q = Vm pmHtot (dX/dt) , где Vm — объемная доля связующего.

Механические деформации e M равняются разности полных деформаций e j и деформаций немеханической природы ^ j :

Для нахождения полных деформаций используются соотношения Коши:

sj = (дui /дxj + дuj /5xi)/2 .

Деформации немеханической природы складываются из вкладов от действия теплового расширения Ъ T и химической усадки Ъ C :

TC

Ъ ij Ъ у 1 Ъ у •

Необходимостью учета истории процесса полимеризации объясняется интегральный вид соотношений для их вычисления:

Ъ ij = f a _y ( T ( t '), X ( t ') )( д T /5 t ‘ ) dt' ,

Ъ C = /ру ( t (t‘), x (t '))(д t/дt‘) dt‘.

Сюда входят компоненты тензоров теплового расширения (ау) и химической усадки (вij) материала, зависящие от температуры и степени полимеризации. Упрощенный вид зависимостей для них предложен в [22]:

a _д

В ij

X <  X ge, , T >  T g ( X ), X >  X ge, , T >  T g ( X )_;

T <  T g ( X ),

X <  X ge, , T >  T g ( X ), X >  X ge, , T >  T g ( X ), T <  T g ( X ).

Здесь индексами L, R и G обозначены постоянные КТР и коэффициенты химической усадки, соответствующие жидкому ( L ), резиноподобному ( R ) и стеклообразному ( G ) состояниям. Величина X_ge , равняется такой степени полимеризации, при которой происходит гелирование связующего, то есть существенное повышение его вязкости. Зависимость температуры стеклования T_g от степени полимеризации может быть задана как явно, так и аппроксимирована любым подходящим образом. В частности, для этих целей здесь используется гипербола, построенная по двум характерным значениям и некоторому параметру X [6]:

Tg - Tg  XX ту - Tg  1 - (1 -X)x ’ где Tg — температура стеклования неполимеризованного связующего; Tg1 — аналогичный параметр для полностью полимеризованной матрицы; X играет роль подгоночного параметра, отвечающего за вид участка гиперболы (выпуклостью вверх или вниз), а также за степень его кривизны: так, значение X = 1,5 соответствует выпуклой вверх, а X = 0,5 выпуклой вниз гиперболе; при X = 1 гипербола вырождается в прямую.

В литературе приводится несколько вариантов определяющих соотношений, служащих для описания процесса отверждения композита. Чаще всего они принадлежат или упругой модели с кусочнопостоянными модулями упругости, или модели с кусочно-линейными упругими модулями [3, 25, 26], или вязкоупругим моделям в различных модификациях [4, 10, 36], а также их упрощениям, например, модели Сванберга [22]. Указанные модели описывают материал в резиноподобном и стеклообразном состояниях.

Определяющие соотношения модели упругости, в которой модули кусочно-постоянны, записываются в виде:

ⁿ j

c Rki г M , t >  T g ( x ), C G г M , T <  T g ( X ),

где C_i^R_jkl и C_i^G_jkl — компоненты тензора модулей упругости в резиноподобном и стеклообразном состояниях соответственно.

Модель с кусочно-линейными модулями, называемая также CHILE (Cure Hardening Instantaneous Linear Elastic), предполагает, что в окрестности температуры стеклования упругие модули изменяются линейно, в то время как в полностью резиноподобном и полностью стеклообразном состояниях они постоянны [3, 25, 26]. В названных работах приводятся формулы для модуля Юнга связующего, которые легко обобщаются на весь тензор модулей упругости:

R ijkl ,

*

< T C 1 ,

C jki (T * ) =

CR + _---'

- ^jkl    T c 2 - T c 1

GR

( ^jkl ^j)l ) ,

^G C ijkl ,

C 2 .

Здесь введено обозначение T * = T g ( X ) - T . Константы T 1 и T 2 являются параметрами материала. Способ определения данных параметров, а также характерная зависимость модуля упругости связующего от температуры и ее аппроксимации в упругой модели и в модели CHILE показаны на рисунке 1.

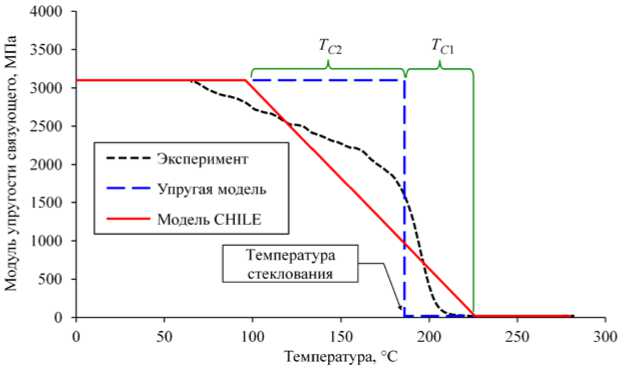
Рис. 1. Характерная зависимость модуля упругости связующего от температуры и ее аппроксимации

Модель Сванберга [22] — это компромисс между упругой (2) и вязкоупругой [4, 10, 36] моделями. Ее определяющие соотношения имеют вид:

^G -j

RM jkl ^г kl ,

GM

- jkl ( ^г kl

-

^{гM (} t tr ) ) ⁺ ^ j ⁽ t_tr ),

T >  T g ( X ), T <  T g ( X ),

где через t_tr обозначено время последнего перехода из резиноподобного в стеклообразное состояние. Из приведенных выражений видно, что приращение напряжений, полученное материалом в стеклообразном состоянии, исчезает при обратном фазовом переходе. Поэтому в области резиноподобного состояния T >  T g ( X ) справедлив закон упругости независимо от того, по какому пути на плоскости фазовых параметров можно попасть в эту область. При новом фазовом переходе стеклования напряжения, соответствующие твердому состоянию, накапливаются заново. Таким образом, упрощенно учитывается зависимость от истории процесса отверждения и деформирования.

Поскольку переход связующего из жидкого в резиноподобное состояние в разных частях композита происходит в различные моменты времени, то для решения задач, в которых наряду с твердым рассматривается и жидкое состояние матрицы, целесообразно прибегнуть к методу «сквозного счета». С его помощью во всей области, занимаемой изделием, решаются одинаковые по структуре уравнения при любом фазовом состоянии материала. В силу того, что в процессе изготовления композита жидкое связующее между волокнами находится в гидростатическом состоянии, достаточно знать только величину давления вне зависимости от поля перемещений. Для нахождения гидростатического давления может быть задействована модель упругости, в которой для изотропного связующего принимается, что K»G, где K и G — модули объемного сжатия и сдвига соответственно. Такая упругая среда, моделирующая жидкость между волокнами, используется далее в процедуре осреднения однонаправленного волокнистого композита.

Задачи отверждения решаются, как правило, в квазистатической постановке со следующими уравнениями равновесия:

∂σ _ij ∂ x_j = 0.

Граничными условиями являются поля перемещений и напряжений на поверхности тела, а также поля температур и потоков тепла. Завершают постановку задачи известные в начальный момент времени распределения температур и степеней полимеризации в рассматриваемом теле.

Изложенный подход применим как отдельно к связующему (при решении микромеханических задач), так и к осредненному материалу на уровне монослоя или ламината.

3.    Свойства материала

В данной работе использован послойный подход к моделированию композита, при котором материал каждого слоя предполагался однородным и ортотропным. Необходимые свойства материала получены методом осреднения [40]. В таблице 1 приведены рассчитанные свойства однонаправленного материала слоя с объемной долей связующего 37% в стеклообразном и резиноподобном состояниях.

Таблица 1. Рассчитанные свойства осредненного материала слоя

Параметр	Значение
	Стеклообразное состояние	Резиноподобное состояние
E 1 , ГПа	152	151
E 2 , E 3 , МПа	6365	140
G 12 , G 13 , МПа	4238	74
G 23 , МПа	2254	45
ν 12 , ν 13	0,31	0,36
ν 23	0,44	0,49
α 11 , К-1	3,96∙10-7	–9,2∙10-8
α 22 , α 33 , К	3,25∙10-5	3,62∙10-5
β 11	–1,73∙10-4	–2,82∙10-6
β 22 , β 33	–1,14∙10-2	–1,27∙10-2
k 11 , Вт/(м∙К)	6,37	6,37
k 22 , k 33 , Вт/(м∙К)	0,52	0,52

В работе рассматривались оснастки из различных материалов: стали, инвара, алюминия и композита. В случае композитной оснастки предполагалось, что она выполнена из того же материала, что и моделируемое изделие, и имеет квазиизотропную укладку. Свойства материалов металлических оснасток, взятые из открытых источников, приведены в таблице 2. Характеристики материала композитной оснастки для уровня ламината и указанной укладки находились путем осреднения свойств из таблицы 1 [26, 40].

Таблица 2. Свойства материалов металлических оснасток

Параметр	Сталь	Инвар	Алюминий
Модуль Юнга, ГПа	200	145	71
Коэффициент Пуассона	0,3	0,3	0,3
Плотность, кг/м3	7800	8130	2700
Теплоемкость, Дж/(кг∙К)	462	510	880
Коэффициент теплового расширения, К-1	1,26∙10-5	1,20∙10-6	2,36∙10-5
Коэффициент теплопроводности, Вт/(м∙К)	29	11	210

4.    Численное моделирование

Определяющие соотношения моделей CHILE и Сванберга были реализованы как собственные программные модули для пакета конечно-элементного анализа Abaqus. С этой целью написаны пользовательские процедуры с названиями UMAT, EUXPAN и HETVAL, каждой из которых при моделировании отверждения отводится своя функция. Так, в теле процедуры UMAT на каждом шаге решается уравнение кинетики полимеризации, рассчитываются мощность внутреннего тепловыделения, деформации теплового расширения и химической усадки, а также механические напряжения. Процедура EUXPAN служит для сообщения программному пакету вычисленных значений деформаций немеханической природы, а процедура HETVAL — для сообщения мощности внутреннего тепловыделения. Обмен данными между процедурами производится через параметры состояния материалов. Пользовательские процедуры, написанные на языке FORTRAN, компилируются в динамически загружаемые библиотеки на этапе

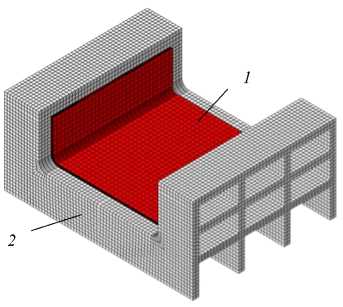
Рис. 2. Конечно-элементная  модель участка лонжерона на оснастке: лонжерон (1), оснастка (2)

решения задачи.

Для численного моделирования был выбран образец, представляющий собой участок лонжерона авиационной конструкции размерами 120×120×40 мм, с толщиной стенки 2,4 мм и последовательностью укладки [+45/-45/90/0/+45/-45] S, где цифры означают градусы, а символ S — симметрию укладки. Такой образец является весьма представительным в силу того, что на нем одновременно можно наблюдать эффекты, связанные с уменьшением прямого угла изделия [12], увеличением кривизны его изначально плоских поверхностей [25, 41] и непосредственным влиянием расширения оснастки [5, 8, 13]. Рабочая поверхность оснастки соответствовала внешней поверхности лонжерона. Моделировался каждый слой изделия. Созданная конечно-элементная модель показана на рисунке 2.

В процессе решения для области контакта изделия и оснастки применялось два типа граничных условий.

Предполагалось, что до момента гелирования связующего изделие может без трения проскальзывать по оснастке, а после этого момента прилипает без возможности самостоятельного отделения. Такой выбор граничных условий обусловлен выводами, сделанными в ходе экспериментальных наблюдений.

Нахождение изделия в печи моделировалось заданием условия конвекции на суммарной свободной поверхности системы изделие–оснастка. После завершения отверждения и охлаждения происходило извлечение изделия из оснастки и его окончательное остывание до комнатной температуры, которая принималась равной 20°C. Между оснасткой и изделием полагался идеальный тепловой контакт. Цикл отверждения изделия с отметками моментов прилипания и отделения от оснастки демонстрируется на рисунке 3.

Особенностью рассматриваемой задачи является длительное время прохождения процесса, что при большом числе конечных элементов в модели приводило к продолжительному численному расчету. Для минимизации вычислительных затрат и сохранения приемлемой точности решения проведена оценка оптимальной величины шага по времени для исследуемого цикла отверждения. С этой целью произведены расчеты отверждения с различными значениями шага по времени на моделях изделий с разнообразной геометрией и разными толщинами ламината. Установленные значения максимальных отклонений от заданной формы сравнивались с «точными» решениями, найденными экстраполяцией полученных

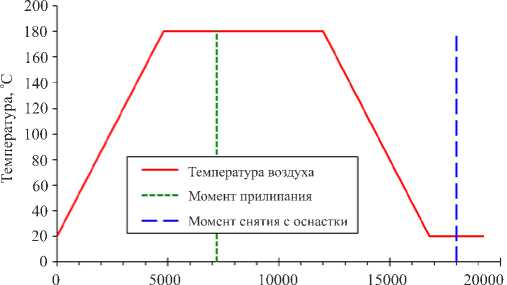
Время отверждения, с

Рис. 3. Цикл отверждения изделия

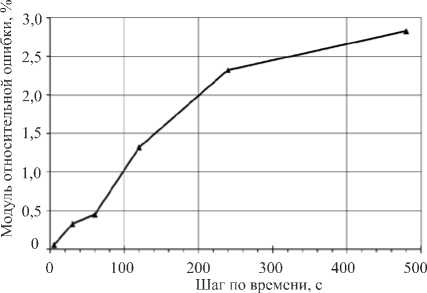
Рис. 4. Зависимость относительной ошибки от величины шага по времени

кривых в область уменьшения шага по времени до нуля. «Точные» решения использовались далее для отыскания абсолютных величин относительных ошибок при различных значениях шага по времени. Наконец, по точкам, соответствующим этим величинам, была построена огибающая кривая, показанная на рисунке 4. Видно, что с ростом размера шага относительная ошибка увеличивается. Эта зависимость стала основой для выбора приемлемой величины шага, который в данной работе составлял 120 с.

Существенную вычислительную трудность создавала также большая поверхность контакта изделия и оснастки, соизмеримая с характерными размерами всей модели. Реализация контактных условий является достаточно ресурсоемкой задачей, поэтому в целях экономии процессорного времени применялась модель контакта с малыми относительными перемещениями и взаимодействием узла со своей проекцией на контактной поверхности.

В ходе работы были произведены расчеты отверждения лонжерона на оснастках из различных материалов по моделям CHILE и Сванберга. Следует, однако, отметить тот факт, что в силу характера рассматриваемого цикла отверждения фазовый переход стеклования в каждой точке конструкции происходил всего один раз. Поэтому в модели Сванберга не действовал механизм «релаксации» напряжений при обратном фазовом переходе. Фактически это означает, что расчет был осуществлен по упругой модели с разрывными модулями.

5.    Результаты расчета

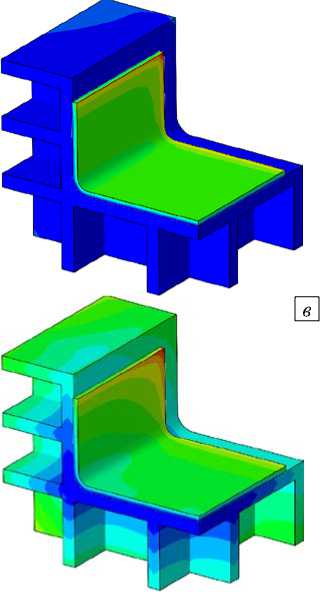
На рисунке 5 показаны картины распределения температуры в модели для различных материалов оснасток через один час после начала цикла отверждения — в момент времени, когда температура воздуха в печи составляла 140°C. Максимальные перепады температуры в оснастке в этот же момент времени приведены в таблице 3.

В процессе нагрева до температуры формования качественная картина распределения температуры в моделях практически не меняется. Как алюминиевая оснастка, так и изделие на ней прогреваются достаточно равномерно в силу большого значения коэффициента теплопроводности алюминия (Рис. 5 а ). В случае оснасток из стали и инвара прогрев их тела становится более неравномерным, а у изделий отмечается заметное повышение температуры свободных углов (Рис. 5 б , в ). Композитная оснастка претерпевает самый большой перепад температуры среди перечисленных (Табл. 3), что объясняется сильной анизотропией коэффициентов теплопроводности в плоскости ламината по отношению к ортогональному направлению. Это приводит к затруднению теплопередачи через толщу ламината оснастки (Рис. 5 г ) и является предпосылкой к локальному перегреву изделия в активной фазе полимеризации.

128,11 127,97 127,82

127,68 127,53 127,39

127,24 127,09 126,95

126,80 126,66 126,51

126,37

120,12 119.75 119,38 119,01 118.64

118,27 117,89 117,52 117,15 116,78

116.41 116,04 115,67

19.1

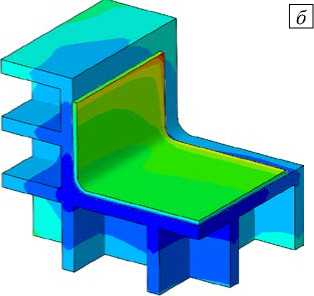
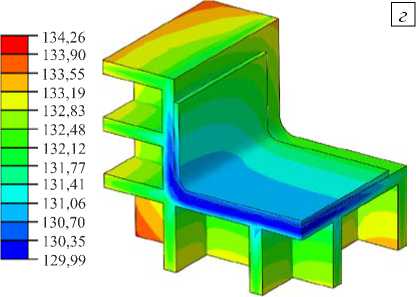
Рис. 5. Распределение температуры (°C) в модели через один час после начала отверждения при использовании различных материалов оснасток: алюминий ( а ), сталь ( б ), инвар ( в ), композит ( г )

Таблица 3. Максимальный перепад температуры оснастки через один час после начала отверждения и максимальный локальный перегрев изделия в активной фазе полимеризации

Материал оснастки	Перепад температуры оснастки, °C	Локальный перегрев изделия, °C
Алюминий	0,16	0,78
Сталь	1,41	0,77
Композит	4,27	2,44
Инвар	3,42	0,89

Вскоре после установления в печи температуры формования у изделия и оснасток из всех рассмотренных материалов имеет место выравнивание температуры, после чего наступает активная фаза полимеризации связующего, характеризующаяся значительной скоростью тепловыделения. Картины на рисунке 5 дают представление об эффективности рассеивания оснасткой избыточного тепла в этом процессе.

В таблице 3 приведены также максимальные значения локального перегрева изделия, зарегистрированные во время активной фазы полимеризации. Наибольший перегрев наблюдается на оснастке из композита. Картину распределения температур в соответствующий момент времени для этой модели содержит рисунок 6. Затруднение отвода тепла через толщу ламината оснастки заметно повышает температуру изделия в его центре, что становится причиной ускоренного протекания реакции

■-182,51 ■ -182,31 ----182,10 --181,90 ---- 181.69 --181,49 --181,29 ----- 181.08 --180.88 ^-180.68 180,47 180.27 180,07

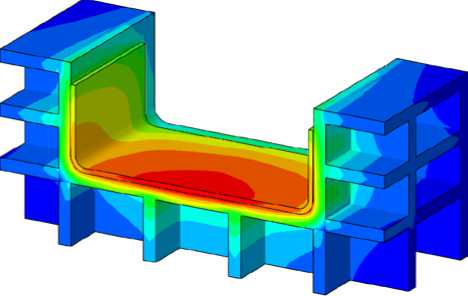
Рис. 6. Распределение температуры (°C) в момент максимального локального перегрева изделия на оснастке из композита

полимеризации в данной зоне в силу зависимости скорости реакции от температуры связующего (см. (1)).

Эволюция степени полимеризации связующего в изделии, располагающемся на композитной оснастке, показана на рисунке 7. Распространение фронта полимеризации начинается со свободных углов изделия в силу их бóльшего прогрева на начальном этапе цикла отверждения. Затем фронт переходит на свободную поверхность изделия, и, наконец, сосредоточивается в центре модели, в области локального перегрева.

0,603 0,602 0,601 0,600 0,598 0,597 0,596 0,595 0,593 0,592 0,591 0,590 0,589

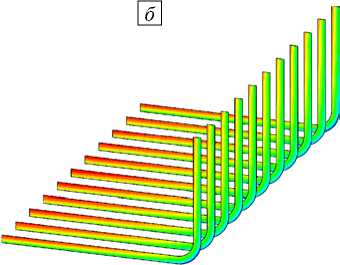
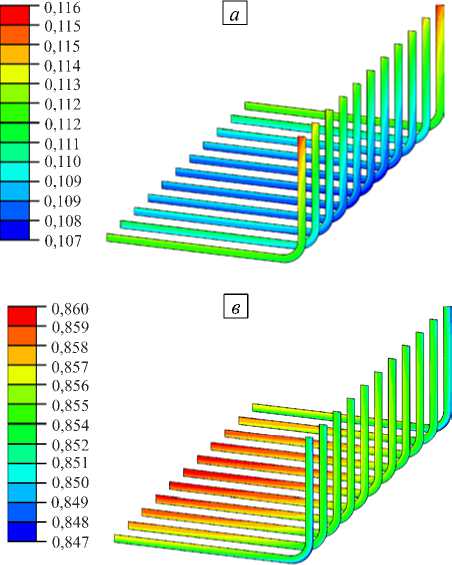
Рис. 7. Распределение степени полимеризации связующего в изделии, находящемся на композитной оснастке, спустя: 4800 с ( а ), 6960 с ( б ), 8400 с ( в )

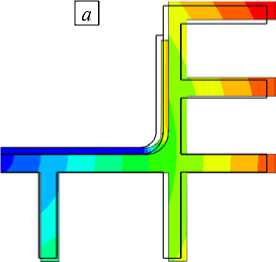
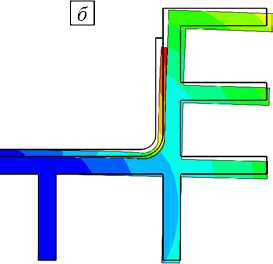
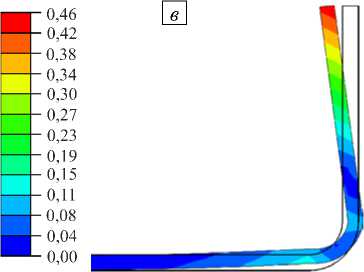
Рис. 8. Поля перемещений (мм) в центральном сечении модели и качественные картины его деформирования в ключевые моменты времени: при температуре формования ( а ), перед снятием с оснастки ( б ), после снятия с оснастки ( в )

Подводя итог, следует отметить, что эффекты неоднородности температурного поля и распределения степени полимеризации не столь ярко выражены в тонких изделиях, таких как исследуемый лонжерон. Но с ростом толщины изготавливаемого ламината они могут стать значительными по величине и послужить причиной дополнительного искажения формы [23].

Распределения перемещений в модели в ключевые моменты времени, а также качественный вид ее деформированного сечения содержит рисунок 8. Рассмотрен случай оснастки из алюминия. Контур недеформированного сечения изображен сплошной линией.

На этапе нагрева до температуры формования изделие практически не сопротивляется температурному расширению оснастки в силу эффекта проскальзывания (Рис. 8 а ), а также своей податливости, обусловленной состоянием связующего до момента его гелирования. Таким образом, отверждение лонжерона целиком происходит в той форме, которую определяет тепловое расширение оснастки. В процессе охлаждения до комнатной температуры связующее оказывается в полностью застеклованном состоянии, что выражается в значительном увеличении жесткости лонжерона. Поэтому к моменту полного остывания оснастка оказывается деформированной из-за наличия сопротивления ее сжатию со стороны изделия (Рис. 8 б ). Наконец, при снятии лонжерона с оснастки происходит переход в новое равновесное состояние, накопленные напряжения перераспределяются, вызывая искажение его формы (Рис. 8 в ).

Эволюция напряженного состояния в окрестности угла изделия показана на рисунке 9. Приведены картины распределения в слоях композита нормальных напряжений, возникающих в центральном сечении модели на различных этапах отверждения. Напряжения σ ₁₁ соответствуют направлению волокон, σ ₂₂ — поперечные напряжения в слое, σ ₃₃ — трансверсальные по отношению к слою. Рассматриваются случай стальной оснастки и модель отверждения CHILE. Контур недеформированного сечения изображен сплошной линией.

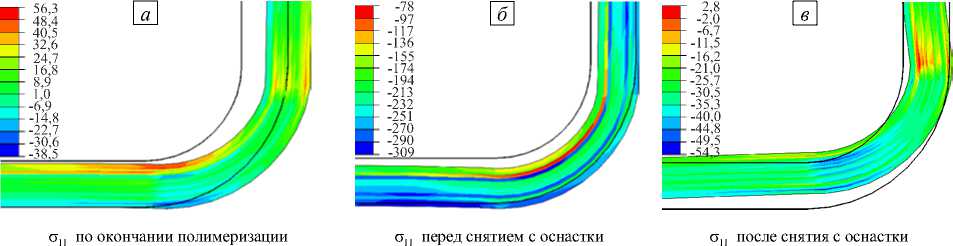
Рис. 9. Распределение нормальных напряжений (МПа) в окрестности угла изделия и качественная картина деформирования в ключевые моменты времени

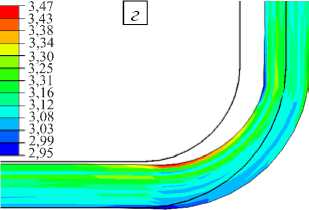
σ ₂₂ по окончании полимеризации

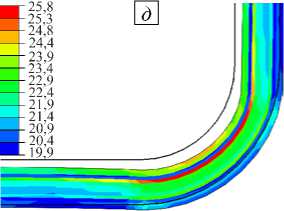
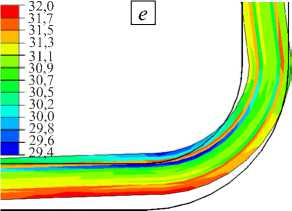
σ ₂₂ после снятия с оснастки

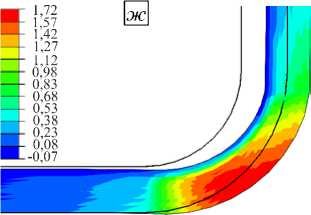
σ ₃₃ по окончании полимеризации

Рис. 9. Продолжение

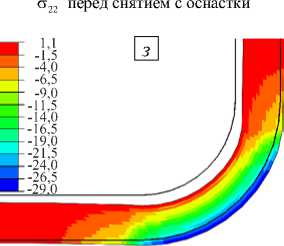
σ ₃₃ перед снятием с оснастки

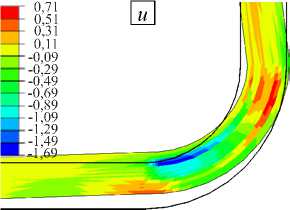
σ ₃₃ после снятия с оснастки

К моменту завершения полимеризации в слоях изделия накапливаются незначительные по величине напряжения. При остывании до комнатной температуры происходят процессы стеклования, а также теплового сжатия материалов оснастки и композита, что выражается в повышении уровня действующих напряжений к моменту полного остывания конструкции. Особенно сильно возрастают продольные сжимающие напряжения (Рис. 9 б ). Их пик достигается в пограничных слоях. При снятии с оснастки конструкция частично разгружается, что вызывает искажения ее формы. Особенно сильно падает уровень продольных сжимающих напряжений σ ₁₁ (Рис. 9 в ). Следует отметить, что в готовой конструкции уровень остаточных напряжений является ненулевым.

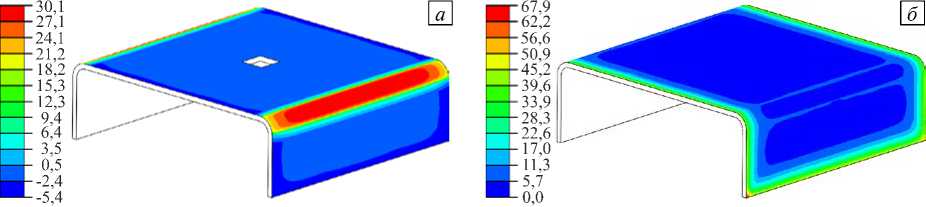
Рис. 10. Распределение контактных напряжений (МПа) перед снятием изделия с оснастки: нормальные напряжения ( а ), касательные напряжения ( б )

На рисунке 10 показаны распределения нормальных контактных напряжений, а также абсолютных величин касательных контактных напряжений перед снятием изделия со стальной оснастки. В расчете использована модель CHILE. Положительный знак нормальных напряжений соответствует прижатию изделия к оснастке.

Перед снятием с оснастки на контактной поверхности существуют области как прижимных напряжений, которые наблюдаются в местах скруглений лонжерона, так и напряжений отрыва на плоских поверхностях. Максимальные величины нормальных напряжений достигаются в области скруглений. Касательные напряжения имеют при этом значительную концентрацию около свободной кромки изделия. Пик касательных напряжений отмечается в свободных углах. При расчете по модели Сванберга распределения контактных напряжений аналогичны представленным на рисунке 10 с разницей лишь в максимальных значениях, которые в данном случае составляют 30,7 МПа у нормальных и 70,9 МПа у касательных напряжений. Это отличие является, в частности, иллюстрацией того, что уровни напряжений в отвержденном изделии при расчете по моделям CHILE и Сванберга получаются разными.

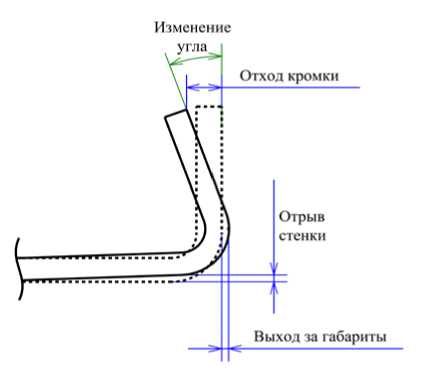
Рис. 11. Параметры искажения формы лонжерона

Типичное искажение формы лонжерона по окончании процесса отверждения характеризуется несколькими параметрами, показанными на рисунке 11. Дефект «отрыва» стенки лонжерона обусловлен взаимодействием изделия с оснасткой в процессе отверждения. Измеренные величины этого дефекта для различных материалов оснасток и моделей отверждения приведены в таблице 4.

Выход за габариты проявляется в увеличении или уменьшении высоты стенки лонжерона по сравнению с теоретическим размером. Количественно этот дефект определяется отношением степени расширения материала оснастки при нагреве и усадки изделия по толщине в процессе отверждения и охлаждения. Таблица 4 содержит измеренные значения. Положительный знак соответствует увеличению габаритов изделия, отрицательный — их уменьшению.

Таблица 4. Искажения формы лонжерона по окончании процесса отверждения

Материал оснастки	Величина «отрыва» стенки (мм)		Выход за габариты (мм)		Абсолютный отход кромки		Относительный отход кромки		Изменение угла (град)
	Модель		Модель		Модель		Модель		Модель
	CHILE	Сванберга	CHILE	Сванберга	CHILE	Сванберга	CHILE	Сванберга	CHILE	Сванберга
Алюминий	0,144	0,124	0,087	0,101	–0,48	–0,35	–0,57	–0,45	–0,99	–0,79
Сталь	0,086	0,073	0,017	0,024	–0,45	–0,36	–0,46	–0,39	–0,81	–0,68
Композит	0,044	0,046	–0,045	–0,053	–0,40	–0,39	–0,36	–0,33	–0,61	–0,58
Инвар	0,027	0,026	–0,046	–0,048	–0,41	–0,40	–0,36	–0,35	–0,62	–0,59

Отход кромок лонжерона в бóльшей мере обусловлен усадкой композита при отверждении в областях скругления, что также приводит к изменению углов изделия [12]. Данная величина может быть оценена в абсолютном и относительном вариантах. Абсолютный отход изображен на рисунке 11 и предполагает замер отклонения от теоретического положения. Относительное значение соответствует отходу кромки от конфигурации, возникшей в результате отверждения, и равняется разности величин абсолютного отклонения и выхода лонжерона за габариты. Последний вариант отбрасывает вклад изменения габаритов лонжерона, поэтому является более показательным. Величины отхода кромки в абсолютном и относительном измерениях приведены в таблице 4. Все значения имеют отрицательный знак, так как кромка лонжерона во всех случаях отклонялась вовнутрь.

Изменение внутренних углов характеризуется поворотом полок лонжерона относительно теоретического положения на определенный угол, который схематично показан на рисунке 11. Величины углов искажения изделий, полученных на оснастках из различных материалов и при разных моделях отверждения, представлены в таблице 4. Все значения отрицательны, так как первоначальный угол вследствие отверждения уменьшается.

6.    Анализ влияния материала оснасток

Наименьший отрыв стенки лонжерона возник при использовании оснастки из инвара, наибольший — при оснастке из алюминия. Сталь и композит показали промежуточные результаты, при этом величина отрыва была меньше у конструкции, изготовленной на композитной оснастке.

У изделий, отвержденных на оснастках из алюминия и стали, произошел положительный выход за габариты, а на оснастках из композита и инвара — отрицательный. Дело в том, что на величине данного дефекта сказались два фактора. Первый — степень усадки изделия во время цикла отверждения; этот параметр во всех рассмотренных случаях был одинаков, а его влияние выражалось в стремлении к уменьшению итоговых габаритов изделия после снятия с оснастки. Второй фактор — степень расширения материала оснастки в результате перепада температуры; он проявлялся противоположно: на начальном этапе процесса отверждения вследствие нагрева оснастка увеличилась в размерах и тем самым определила габариты заготовки до начала полимеризации связующего. Процесс полимеризации целиком проходил при температуре, близкой к 180°, и завершился стеклованием, в результате чего конструкция «застыла» в той форме, которую обусловила оснастка.

Из перечисленных материалов алюминий обладает самым большим КТР. По этой причине выход за габариты изделия, изготовленного на алюминиевой оснастке, характеризуется положительным знаком и самым большим значением, поскольку эффект расширения оснастки значительно перекрывает эффект усадки композита. У стали КТР ниже, чем у алюминия, поэтому величина рассматриваемого дефекта у изделия, отвержденного на стальной оснастке, заметно меньше, чем в случае использования алюминиевой. Выход за габариты имеет здесь положительный знак и самую малую абсолютную величину. Это говорит о том, что эффект расширения стальной оснастки преобладает над эффектом усадки композита несущественно, и они в значительной степени компенсируют друг друга. Порядки величин КТР композита (в плоскости ламината) и инвара одинаковы, но сами значения коэффициентов достаточно малы по сравнению со значениями КТР для алюминия и стали. Поэтому выход за габариты у конструкций, полученных на указанных оснастках, примерно одинаков, с отрицательным знаком, и свидетельствует о преобладании в них усадки при отверждении над степенью расширения оснасток из названных материалов.

Для качественной оценки влияния материала оснастки на форму изделия важна разность величин выхода за габариты и абсолютного отхода кромки, которая в данной работе определена как относительный отход кромки. Дефект достигал наименьшей абсолютной величины при использовании в процессе изготовления изделия оснасток из композита и инвара. Худший результат показала алюминиевая оснастка.

Изменение угла лонжерона есть интегральный параметр. По нему можно достоверно судить о степени искажения изделия оснасткой из того или иного материала. Как композитная, так и инваровая оснастки вызывали изменения угла с наименьшей абсолютной величиной, а оснастка из алюминия — с наибольшей.

Из анализа величин перечисленных дефектов вытекает, что по совокупности факторов оснастка из инвара является лучшей с точки зрения качества производимого изделия. Композитная оснастка лишь по одному параметру уступает инваровой, поэтому с равным успехом применима для изготовления высокоточных композитных конструкций при гораздо меньших материальных затратах по сравнению с оснасткой из инвара. Стальная оснастка наиболее доступна, но уровень величин сопутствующих дефектов при этом выше при сопоставлении с названными выше материалами. Оснастка из алюминия — худшая по всем исследованным параметрам; ее использование негативно сказывается на качестве изделия. Поэтому данный материал не рекомендуется для производства композитных конструкций с жесткими требованиями к точности соблюдения формы.

Легко видеть, что материалы оснасток, перечисленные в порядке ухудшения качества изделия,

Таблица 5. Связь качества изделия с КТР оснастки

Материал оснастки	Качество изделия	КТР·10–6, К –1
Инвар	Лучшее	1,20
Композит	Хорошее	2,02
Сталь	Среднее	12,6
Алюминий	Плохое	23,6

располагаются в той же последовательности, что и с увеличением их КТР (Табл. 5). Из этого обстоятельства, а также из описанных выше механизмов искажения формы, следует вывод о том, что качество создаваемого изделия связано не только со свойствами композита, но и с величиной КТР оснастки. Эту закономерность можно сформулировать так: чем ниже КТР оснастки, тем более качественным (с меньшими искажениями формы) получается изделие.

В заключение необходимо отметить, что у оснасток из рассмотренных материалов имеются и свои недостатки. Так, слабое место оснастки из композита — ее небольшой ресурс, а также деградация свойств из-за высоких перепадов температуры. Инвар же достаточно дорог и труден в обработке. Поэтому выбор материала оснастки на практике определяется в бóльшей степени технологическими и экономическими соображениями, а также величинами разрешенных допусков для того или иного типа изделия.

7.    Заключение

В статье обсуждается моделирование отверждения композитных конструкций с учетом оснастки. Проведено теоретическое сравнение моделей отверждения композита с термореактивным связующим. Предложена модель контакта, включающая переход от проскальзывания к прилипанию в момент гелирования связующего. Созданы программные модули для реализации расчета по моделям CHILE и Сванберга в пакете конечно-элементного анализа Abaqus.

Известные из литературы идеи моделирования отверждения нашли в данной работе дальнейшее развитие, характерными особенностями которого являются:

• –    решение термомеханической задачи отверждения изделия с учетом тела оснастки;

• –    введение в модель механического и теплового контакта между оснасткой и изделием;

• –    смена условия контакта в процессе решения задачи;

• –    описание нагрева системы изделие–оснастка посредством граничных условий типа конвекции;

• –    оценка оптимального шага по времени;

• –    моделирование каждого слоя композита в изделии.

С помощью разработанного программного модуля осуществлены расчеты отверждения участка лонжерона на оснастках из различных материалов. Вычислены поля температуры в процессе нагрева до температуры формования, продемонстрированы эволюции степени полимеризации и напряженно-деформированного состояния изделия в процессе отверждения. Даны типичные картины распределения контактных напряжений перед снятием с оснастки. Показано, что эффект теплового расширения оснастки вносит существенный вклад в качество изготавливаемого композита. Так, для материалов с большими КТР наблюдались более сильные искажения формы конструкции по сравнению с материалами, характеризуемыми малыми КТР. Сделан вывод о том, что оснастки из инвара и композита дают лучший результат с точки зрения качества изготавливаемого изделия.

На данном этапе авторами проделан лишь сравнительный анализ влияния материала оснастки на форму изделия, опирающийся только на результаты численного расчета. Полученные искажения формы качественно согласуются с результатами для деталей аналогичной конфигурации, многообразие которых доступно в открытых информационных источниках. Количественное сравнение на основе собственных экспериментальных сведений планируется выполнить и представить на обсуждение в будущем.

Авторы благодарят А.В. Кепмана, А.В. Бабкина, А.В. Солопченко и Е.С. Афанасьеву за помощь в проведении исследований.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.31.0114 от 14 августа 2014 г. в составе мероприятий по реализации Постановления Правительства РФ № 218, шифр 2014-218-05-8228).