Моделирование влияния примеси на туннельный ток контакта полимера с квантовыми точками и металлом

DOI:

Другим интересным вопросом остается исследование туннельных характеристик контактов наноструктур с другими материалами (металлом, квантовыми точками). Данные исследования позволяют оценить пригодность использования различного рода структур в качестве высокочувствительных детекторов газов, а также тяжелых металлов [6]. В работах [4; 5] была предложена методика расчета туннельного тока контакта графеновых нанолент различной формы с металлом и квантовыми точками, в том числе с учетом внешнего запирающего электрического поля. Плотность состояний была рассчитана с помощью предварительной диагонализации гамильтониана для электронов графена. Очевидным образом возникает задача изучения туннель- ных характеристик полимеров, поскольку именно они все чаще используются в качестве подложек для графена, а также в составе композиционных материалов.

В данной работе в качестве полимерной структуры выберем полиацетилен (ПА), возможные формы которого приведены на рисунке 1. Наиболее привлекательной с точки зрения практических приложений формой являются пленки полиацетилена (цис-формы).

цис-форма

транс-форма

Рис. 1. Структура полиацетилена

Данные ядерного магнитного резонанса и рентгеновской дифракции показывают, что длины связей между атомами C различаются на 0,03–0,04 Å (двойная связь оказывается короче). Такое незначительное отличие длин оказывает существенное влияние на электронные свойства ПА, его зонную структуру.

Закон дисперсии для полиацетилена имеет вид:

E i , 2 ( q ) = ±aJ ( ^a o sin ( qa о ) ) 2 ⁺ ( ² t o cos ( qa 0 ) ) 2

2n n qa о = —, n = 0, ±1,

± N

здесь Δ₀ = 4αy = 0,7 eV; t ₀ = 2,5 eV; N – число атомов в решетке.

Из формулы (1) очевидно, что на уровне Ферми открывается зонная щель, при этом валентная зона заполнена полностью, а зона проводимости оказывается пустой.

Одномерный решеточный гамильтониан для рассматриваемого полимера может быть записан в виде [2]:

^H p =- £ t n , n + 1 ( c ⁺+ 1 A, s ⁺ c . c . ) ⁺ 0.5 ^K E ( У п + 1 - У п ) ^{2 +} 0.5 ^M £ У п n , s                                                     n                                        n

tn,n+1 = t0 - a(Уп+1 - Уп ) , Уп = (-1)n • У, где s – спин; n – номер (CH)-группы; yn – конфигурационные координаты для каждой (CH)-груп-пы, описывающие трансляцию вдоль линейного остова цепочки; M – масса группы (CH); K – упругая постоянная. Отметим, что K = 21 eV/Å2, α = 4,1 eV/Å, y = 0,04 Å.

Последним слагаемым в уравнении (2) можно пренебречь в силу того, что мы рассматриваем близкий к статическому случай. А для него это слагаемое можно учесть с помощью перенормировки.

Для 5 групп (СН) гамильтониан в матричной форме будет выглядеть следующим образом:

n	1	2	3	4	5
1	' 2 Ку 1	-t t 1 , 2	0	0	0 ^
2 Hn =	- t 1 ,1	2 Ky 2	t 2 , 3	0	0
p 3	0	-t t 2 , 3	2 Ky 2	- t 3 , 4	0	.                               (3)
4	0	0	t 3 , 4	2 Ky 2	- t 4 , 5
5	I 0	0	0	- t 4 , 5	2 Ky 2 ;

Учет влияния примеси в матричном виде демонстрируется в формуле (4):

H =

( H

H

^ mt

^H int

E imp у

здесь E_imp – матрица, на диагонали которой энергетические уровни примеси; H_int – матрица, содержащая энергии переходов между определенным уровнем примеси и (CH)-группой.

Далее на основе собственных значений матрицы нами рассчитывалась плотность состояний для полиацетилена νА путем прямого подсчета количества энергетических уровней в заданном интервале энергий. Плотность тока контакта вычислялась в рамках теории Кубо [1]:

to

J un = ^{4 n} e\^T Г J d ^EV A ^{( E} + e^{U V} B ^{( E )(} n f ^{( E} ) - n f ^{( E} + e^U )

-to

^v a ^{( e )} = E ^{8 ( E} - ^E A ) V B ^{( e )} = Ъ ^{S ( e} — ^E B );

pq где 8(x) - дельта функция Дирака, vA(B)(e) - туннельная плотность состояний; nf(s) - равновесное число фермионов с энергией s; U - разность потенциалов между контактами. Здесь и далее используется приближение «шероховатого» контакта Т (матричный элемент оператора туннелирования между состояниями p и q): Tpq = T (плоскость графена перпендикулярна к поверхности контактного материала).

В качестве материалов, с которыми полиацетилен вступает в контакт, выберем металл (6) и квантовые точки (7). Электронный спектр для них можно записать в следующем виде:

ε

А - Р q   2m,

здесь p – импульс; m – эффективная масса электрона.

Et - E0 -Аcos(Р ),

S o - энергия электронов квантовой ямы; А - интеграл туннелирования, определяемый перекрыванием электронных волновых функций в соседних ямах; р – квазиимпульс.

После вычисления интегралов, входящих в (5), с учетом свойств дельта-функции легко получить вольтамперную характеристику контакта.

Зависимость плотности туннельного тока (контакт с металлом и квантовыми точками) для полиацетилена от напряжения представлена на рисунках 2 и 3.

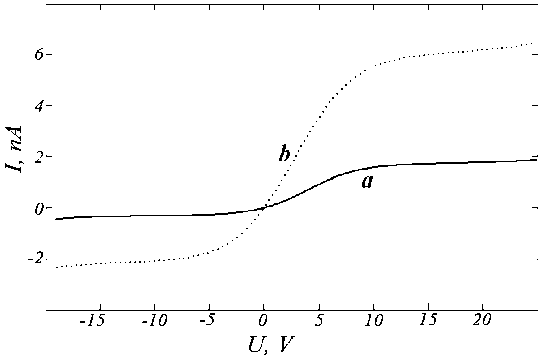
Рис. 2. Зависимость туннельного тока от напряжения для контакта полимера с металлом: a – без примеси; b – с учетом примеси

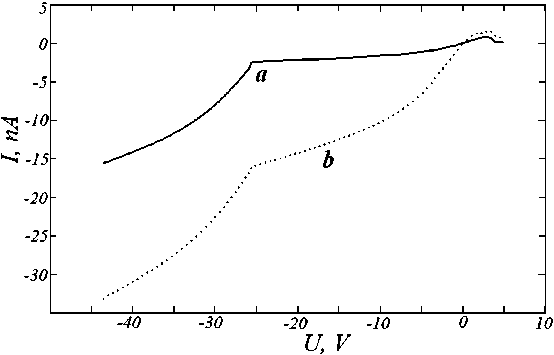
Рис. 3. Зависимость туннельного тока от напряжения для контакта полимера с квантовыми точками: a – без примеси; b – с учетом примеси

Как видно из рисунка 2, введение примеси существенно влияет на форму ВАХ для контакта с металлом, что проявляется в увеличении тока в положительной по напряжению области, и в его уменьшении – в отрицательной.

Что касается контакта полимера с квантовыми точками (рис. 3), то здесь характер ВАХ практически не изменяется в случае введения примеси, уменьшается только величина электрического тока.

Из полученных результатов можно заключить, что введение примеси позволяет контролировать величину туннельного тока в системе, в том числе добиваться его увеличения. Это обстоятельство может оказаться полезным при разработке устройств, основанных на туннельном эффекте (диоды, транзисторы).

В дополнение к вышесказанному можно сделать вывод о возможности применения данной полимерной структуры при обнаружении примесных молекул как самостоятельно, так и в качестве подложки, например, для графена, который себя уже хорошо зарекомендовал как высокочувствительный сенсор.