Моделирование возбуждения поверхностных плазмон-поляритонов в прямоугольном нанорезонаторе на основе золота

Поверхностные плазмон-поляритоны (ППП) – электромагнитные возбуждения в оптическом диапазоне частот, распространяющиеся в тонком слое на границе раздела металл–диэлектрик. ППП представляют собой связанные колебания электромагнитного поля в диэлектрике и электронной плазмы металла с отрицательной действительной частью диэлектрической функции [1].

Первое математическое описание поверхностных волн было представлено А. Зоммерфель-дом в 1899 г. [2], а первый эксперимент, в котором наблюдался поверхностный плазмон-поляритон, провел Р. Вуд в 1902 г. [3]. Решения уравнений Максвелла, найденные в 1907–1909 гг. Дж. Ценнеком и А. Зоммерфельдом [4, 5] при рассмотрении задачи о распространении радиоволн вдоль поверхности металла с конечной проводимостью, полностью применимы для описания ППП на границе раздела проводник–диэлектрик. Во второй половине XX века Р. Ритчи провел детальное исследование ППП в тонких металлических пленках [6], а в 1968 г. Кречман и Рэ-тер представили общее описание возмущения поверхностных волн видимым светом [7].

Сильная локализация ППП позволяет рассматривать процессы на наномасштабах (электромагнитное излучение мало проникает в металл, оказываясь «запертым» в области, размеры которой в несколько раз меньше длины волны излучения), в настоящее время активно изучается возможность использования структур, поддерживающих ППП. Плазмонные волноводы могут быть применены для уменьшения размеров интегральных схем и увеличения скорости их работы, однако металлические наноструктуры обладают омическими потерями, которые необходимо компенсировать для увеличения длины пробега ППП в структуре [8]. Структуры, поддерживающие распространение ППП, могут быть использованы для создания новых типов устройств в наноэлектронике. Так, сенсоры, использующие факт чувствительности поверхностных плазмонов к изменению диэлектрических свойств среды вблизи поверхности раздела, могут быть использова- ны в биологии и химии для анализа белков и концентраций веществ. Спазеры (Surface Plasmon Amplification by Stimulated Emission of Radiation – усиление поверхностных плазмонов посредством вынужденного излучения), поверхностные плазмон-поляритоны в которых играют роль фотонов в лазерах. Спазеры состоят из квантовой точки, расположенной вблизи металлической наночастицы, и создают ближнее поле вместо излучения дальних полей, как в лазере. Спазеры могут быть использованы в спектроскопии: устройство состоит из металлической иглы, поддерживающей существование ППП. Спазер создает интенсивное поле в субволновой области пространства, вследствие чего обеспечивается высокая эффективность взаимодействия ППП с исследуемым образцом, полученный сигнал подается на анализатор спектра [10].

Исследование возбуждения ППП в ограниченной наноструктуре раздела золото–оксид кремния обладает потенциалом для развития науки и техники: в оптическом диапазоне золото обладает наименьшими омическими потерями в сравнении с другими металлами, оксид кремния обеспечивает локализацию электромагнитного поля в поперечном направлении.

Рассмотрим возбуждение ППП в ограниченной прямоугольной наноструктуре – нанорезонаторе. Наноструктура представляет собой границу раздела между диэлектриком и металлом, заполняющими полупространства. Над поверхностью металла расположен источник электромагнитного излучения, возбуждающий ППП. На поверхности металла выделен прямоугольник размерами L x , L y , в котором рассматривается волновое поле.

Дискретная модель волнового поля в прямоугольной области – двумерная решетка связанных цифровых дискретных фильтров [11]. Такая модель зарекомендовала себя и неоднократно применялась для описания возбуждения двумерного волнового поля ансамблем осцилляторов в различных структурах: круглой мембране; двумерной области в виде кругового кольца с гофрированной границей [12, 13].

Итерационная динамика волнового поля, возбуждаемого осцилляторами в прямоугольной области:

u ( x , y , t + 1 ) = a 1 u ( x , y , t ) - a ₂ u ( x , y , t - 1 ) + bW ( t , x ± 1, y ± 1 ) + gF ( x , y , t ) ,        (1)

где W ( t , x ± 1, y ± 1 ) = u ( x - 1, y , t ) + u ( x + 1, y , t ) + u ( x , y - 1, t ) + u ( x , y + 1, t ) .

Функция u(x,y,t) описывает состояние волнового поля в точке с координатами x, y в момент времени t; время t изменяется дискретно, x, y также изменяются дискретно с единичным шагом, g – коэффициент связи волнового поля с осцилляторами. Связь коэффициентов модели с безразмерными параметрами – фазовой скоростью волны v и декрементом затухания γ a1 = 2(2v2 -1)eY, a2 = e2Yy, b = v2e-Y.                             (2)

Для устойчивости решений уравнения (1) безразмерная скорость v в модели не должна превосходить 1Д/2 .

Пространственные координаты принимают значения 0 ≤ x ≤ Lx, 0 ≤ y ≤ Ly. По координате x были приняты следующие граничные условия u (0; y; t ) = u (1; y; t);(3)

u (Lx; y; t )=u (Lx-1; y; t).

Граничные условия по продольной координате y u (x ;0; t ) = u (x ;1; t);(5)

u(x;Ly;t) = u (x;Ly -1;t).(6)

Действие точечных осцилляторов на поле

N

F (x, y, t ) = ^^ (x - x (n ))J (y - y (n)) z (n, t).(7)

n = 1

Для моделирования возбуждения ППП точечным источником, размещенным вблизи поверхности металла, будем считать, что динамика источника удовлетворительно описывается уравнением Ван дер Поля в дискретном случае при малых параметрах нелинейности источника [14].

Динамика осциллятора, взаимодействующего с волновым полем, определяется нелинейным уравнением

z (n, t +1) = d1 (z) z (n, t)- d2 (z) z (n, t -1) + gAu (x (n ),y (n ),t) , где Au (x (n), y (n ), t) = u (x ( n), y (n ), t)- u ( x (n ), y ( n), t -1) .

Коэффициенты уравнения зависят от состояния осциллятора следующим образом:

d 1 = 2exp ( ^ ( 1 - a z ² ( n , t ) ) ) cos ( в ) , d ₂ = exp ( 2 ^ ( 1 - a z ² ( n,t ) ) ) , где β – частота осциллятора, α, ε – его нелинейные параметры.

Из дисперсионного соотношения для ППП на одиночной границе раздела металла с диэлектрической функцией ε 1 (Re( ε 1 ( ω )) <  0) и диэлектрика с диэлектрической проницаемостью ε 2 получается выражение для фазовой скорости

to vph = ” = -spp

£ 1 + £ 2

.

После преобразований получим vph ="—cT= ^I £1 |2 +^2 (Re (^1)- i •Im(^1 I £1I ^£2

Обозначим

vph = с • v = ( Re ( v ) + i Im ( v ))• c.

Частота воздействия задается выражением

2π ω=ck=c .

λ

Диэлектрическая проницаемость кварцевого стекла ε 2 = 4, плазменная частота золота to p = 1,39^10 16 Гц. При длине волны излучения X = 1,5-lG^-6 м частота воздействия to ~10¹⁵ Гц, диэлектрическая функция золота £ 1 =- 190 + 19 i ; | £ 1 1 = 191. Таким образом, значение v = 0,5 + 10 ^{- 4} i .

Действительная часть выражения (12) отвечает за фазовую скорость волны и имеет вид

^Re ⁽ v Ph ) =v ^ ’

где v – безразмерная скорость волны в модели. Из условия устойчивости решений уравнения (1), параметр v <1/√2. Сравнивая полученное значение коэффициента v и выражение (14), можем Ar принять отношение      равным скорости света, т.к. действительная часть коэффициента

A t

Re ( v ) = 0,5 <  1Д/2. Мнимая часть выражения (12) отвечает за декремент затухания электромагнитной волны.

Будем считать, что шаг сетки Δ r цифровых фильтров, являющейся дискретной моделью двумерного волнового поля в прямоугольном резонаторе, по порядку величины составляет 1 нм. Тогда характерное время Δ t по порядку величины составляет 10^–18 с = 1 ас.

Безразмерная частота осциллятора связана с характерным временем как в = — At = - At.                               (15)

2п    A

Тогда при λ = 1,5·10^–6 частота осциллятора составляет β ~ 6·10^–4.

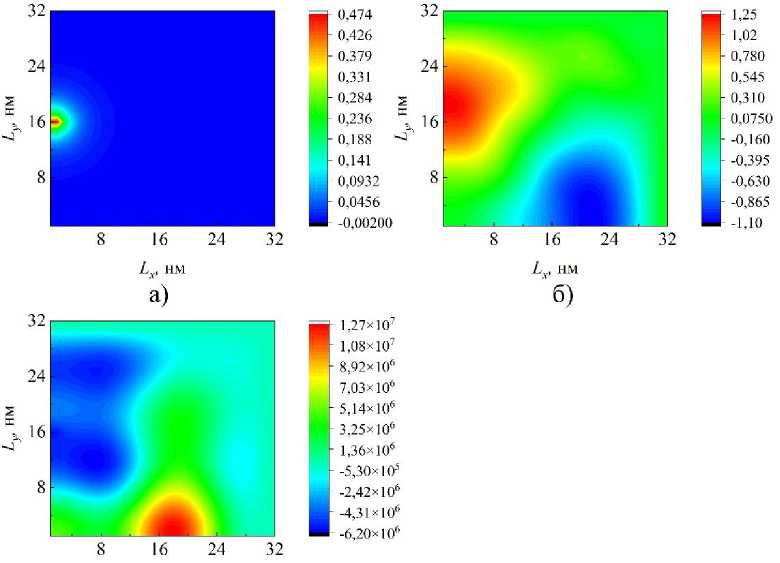
Рассмотрим распределения резонансного волнового поля, рассчитанные на основании дискретной модели (1)–(9) в структуре с размерами Lx = 32 нм, Ly = 32 нм по прошествии длительно- го времени. Частота осциллятора β принимается равной 0,0006; коэффициент связи волнового поля с осциллятором g принимается равным 0,1; 0,25 и 0,5. На рис. 1 стационарное волновое поле рассчитано при размещении осциллятора в точке (1;16) данной структуры, на рис. 2 – при смещении осциллятора в центр рассматриваемой структуры.

L_x, нм

в)

Рис. 1. Волновое поле в структуре с размерами L x = 32 нм, L y = 32 нм, осциллятор в точке (1;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осциллятором a) g = 0,1; б) g = 0,25; в) g = 0,5

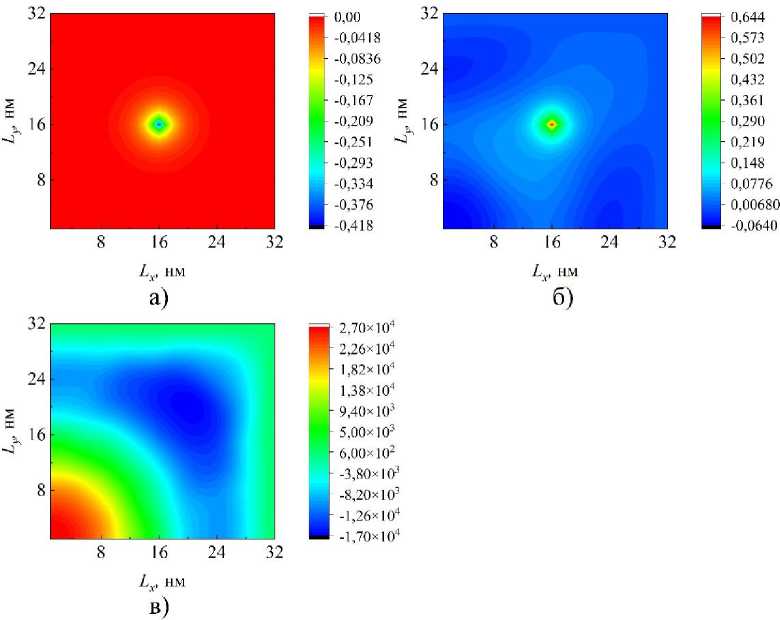
Рис. 2 Волновое поле в структуре с размерами L x = 32 нм, L y = 32 нм, осциллятор в точке (16;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осциллятором a) g = 0,1; б) g = 0,25; в) g = 0,5

На рис. 1 и 2 видно, что при малых значениях коэффициента связи волнового поля с осцилляторами g преобладает равномерная составляющая поля. При увеличении данного параметра значительно меняется модовый состав, а также существенно увеличивается амплитуда резонансного волнового поля. Когда осциллятор располагается у края нанорезонатора, можно отметить, что увеличение коэффициента связи влияет на изменение модового состава сильнее, чем при расположении осциллятора в центре структуры.

Для выявления модового состава волнового поля в нанорезонаторе вычислим его преобразование Фурье по пространственным координатам, получим набор коэффициентов - амплитуд мод резонансного волнового поля

u(fk,fn)=£ Eunexp -i21^k^exp -i2^n = £ '^икпcos 2^k+2^n - k=0 n=0 V Lx ) V Ly ) k=0 n=0 ^ Lx Ly )

-^ ¹ £ ¹ U kn ™[ ^ k + ^ n 1 (16) k = 0 n = 0 V L x L y )

где k - число длин волн (максимумов), укладывающихся на стороне L x , n - число длин волн (максимумов), укладывающихся на стороне L y . Пространственное преобразование Фурье позволит также проанализировать эволюцию модового состава волнового поля с течением времени.

На рис. 3 приведены пространственные преобразования Фурье волнового поля в структуре с размерами L x = 32 нм, L y = 32 нм при различных значениях параметра связи волнового поля с осцилляторами g, осциллятор с частотой в = 0,0006 помещен в точку (1;16). На рис. 4 показаны пространственные преобразования Фурье волнового поля в рассматриваемой структуре с осциллятором, помещенным в точку (16; 16).

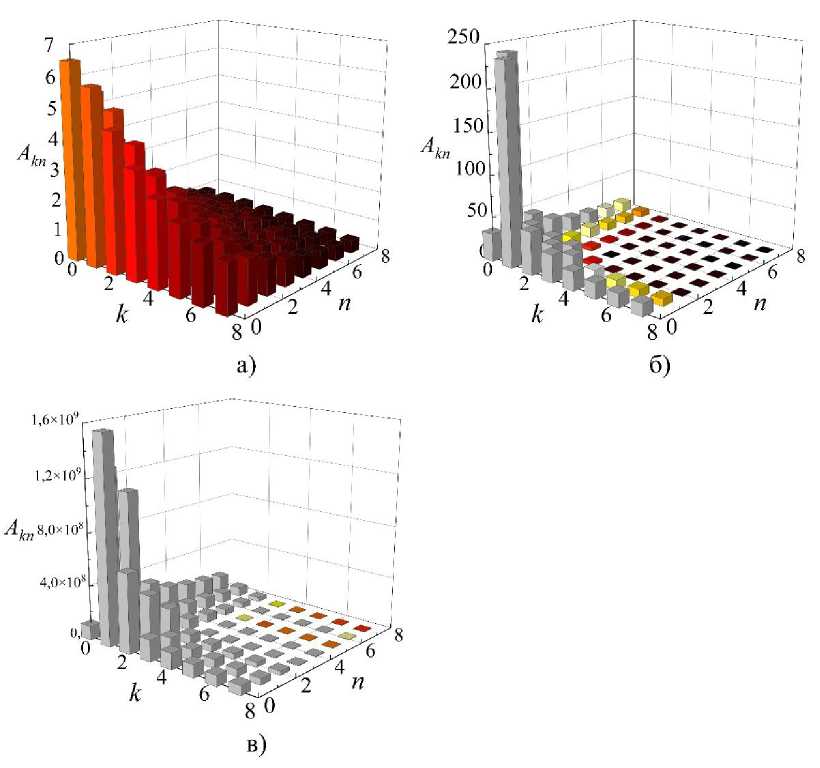
Рис. 3 Амплитуды возбуждаемых мод с индексами ( k; n ) волнового поля в структуре L x = 32 нм, L y = 32 нм, осциллятор помещен в точку (1;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осцилляторами а) g = 0,1; б) g = 0,25; в) g = 0,5

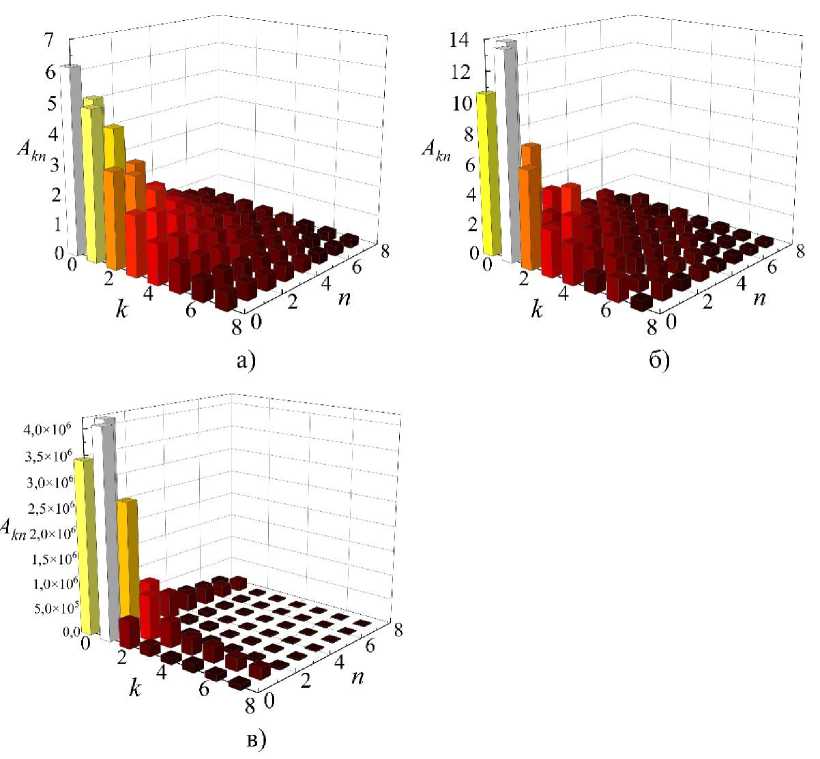
Рис. 4 Амплитуды возбуждаемых мод с индексами ( k ; n ) волнового поля в структуре L x = 32 нм, L y = 32 нм, осциллятор помещен в точку (16;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осцилляторами а) g = 0,1; б) g = 0,25; в) g = 0,5

Видно, что в рассматриваемой структуре наибольшую амплитуду имеют моды резонансного волнового поля низших порядков: (0;0), (1;0) и (0;1). Когда коэффициент связи волнового поля с осцилляторами g = 0,1, преобладает мода (0;0). При увеличении данного параметра амплитуда мод (1;0) и (0;1) значительно возрастает, намного превышая амплитуду моды (0;0).

Также можно отметить, что в случае расположения осциллятора у края нанорезонатора амплитуда возбуждаемых мод превосходит амплитуду мод волнового поля в структуре с осциллятором, расположенным в центре. Из этого можно сделать вывод, что расположение источника колебаний у края нанорезонатора более эффективно для возбуждения резонатора в одномодовом

режиме.

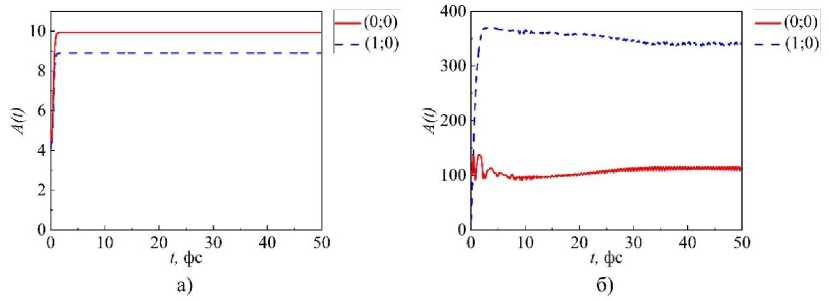
Рис. 5 Временная эволюция амплитуд мод ( k; n ) резонансного волнового поля в структуре с размерами L x = 32 нм, L y = 32 нм, осциллятор в точке (1;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осцилляторами a) g = 0,1; б) g = 0,25

Рассмотрим изменение огибающих амплитуд возбуждаемых мод волнового поля в структуре с течением времени. На рис. 5 приведена временная эволюция амплитуд мод волнового поля в нанорезонаторе с размерами L x = 32 нм, L y = 32 нм при значениях коэффициента связи волнового поля с осцилляторами g = 0,1 и 0,25. Осциллятор с частотой в = 0,0006 расположен в точке (1; 16).

При значении g = 0,1 на рис. 5, а огибающая амплитуд прекращает свой рост приблизительно после наступления времени t = 2 фс, огибающая амплитуды моды (0;0) превосходит огибающую (1;0). Т.к. динамика источника электромагнитной волны описывается уравнением Ван дер Поля при малой нелинейности параметров, в системе устанавливается равновесие между энергией, теряемой в резонаторе за счет омических потерь, и энергии, поступающей от осциллятора.

При значении g = 0,25 на рис. 5, б огибающая амплитуда моды (1;0) достигает максимума приблизительно при t = 4 фс и превосходит огибающую (0;0) более, чем в три раза, причем, с течением времени амплитуда моды (1;0) медленно снижается, приблизительно при t = 35 фс выходит на стационарную амплитуду. В промежутке времени до t = 10 фс огибающая амплитуды моды (0;0) проходит через ряд локальных максимумов и минимумов, а после времени t = 30 фс огибающая испытывает выход в стационарный режим.

Рассмотрим эволюцию амплитуд мод волнового поля в нанорезонаторе с размерами L x =32 нм, L y = 32 нм с течением времени. Осциллятор с частотой в = 0,0006 расположен в точке (1; 16) коэффициент связи волнового поля с осцилляторами g = 0,5

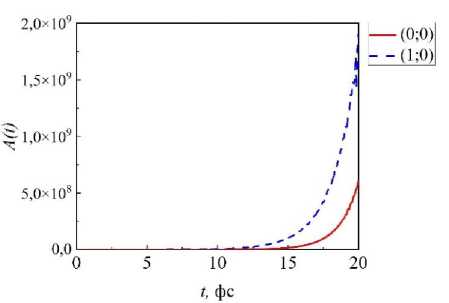
Рис. 6 Временная эволюция амплитуд мод ( k; n ) резонансного волнового поля в структуре с размерами L x = 32 нм , L y = 32 нм, осциллятор помещен в точку (1;16), частота осциллятора β = 0,0006, коэффициент связи волнового поля с осцилляторами g = 0,5

На рисунке 6 видно, что при g = 0,5 амплитуда возбуждаемых мод неограниченно возрастает, причем, амплитуда моды (1;0) при t = 20 фс превышает амплитуду моды (0;0) более, чем в два раза. Это свидетельствует о том, что при больших значениях коэффициента g модель перестает быть устойчивой и не может быть применена для корректного моделирования возбуждения поверхностных плазмон-поляритонов в ограниченной наноструктуре.

Таким образом, в данной статье на основе дискретной модели волнового поля, возбуждаемого осцилляторами, было теоретически исследовано возбуждение поверхностных плазмон-поляритонов в ограниченной прямоугольной наноструктуре, состоящей из золота и кварцевого стекла: для моделирования возбуждения поверхностных плазмон-поляритонов в металлической структуре были рассчитаны значения фазовой скорости, частоты источника излучения, а также значения характерного времени в системе, получены распределения волнового поля в прямоугольной области и проведено преобразование Фурье резонансного поля по пространственным координатам и проанализирована временная эволюция амплитуд возбуждаемых мод волнового поля при различных коэффициентах связи волнового поля с осцилляторами и при различных положениях осциллятора. Увеличение коэффициента связи волнового поля с осцилляторами g приводит к росту амплитуд возбуждаемых резонансов. Особенно сильно возрастают амплитуды мод (1;0) и (0;1). При величине g > 0,5 амплитуда волнового поля неограниченно возрастает, как и амплитуда колебаний осциллятора, что говорит о неустойчивости модели в таком диапазоне параметров. Так, полученные результаты могут быть полезны для создания заданного распределения интенсивности поверхностных плазмон-поляритонов в наноструктурах.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (№ 075-01493-23-00).

• 1.    Майер, С.А. Плазмоника: теория и приложения / С.А. Майер. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2011. – 296 с.

• 2.    Sommerfeld, A. Ueber die Fortpflanzung elektrodynamischer Wellen l¨angs eines Drahtes / A. Sommerfeld // Ann. Phys. – 1899. – Vol. 303. – P. 233–290.

• 3.    Wood, R.W. On a Remarkable Case of Uneven Distribution of Light in a Diffraction Grating Spectrum / R.W. Wood // Proceedings of the Physical Society of London. – 1902. – Vol. 18, no. 1. – P. 269–275.

• 4.    Zenneck, J. Über die Fortpflanzung ebener elektromagnetischer Wellen längs einer ebenen Leiterfläche und ihre Beziehung zur drahtlosen Telegraphie / J. Zenneck // Ann. Phys. – 1907. – Vol. 328, Iss. 10. – P. 846–866.

• 5.    Sommerfeld, A. Uber die Ausbreitung der Wellen in der drahtlosen Telegraphie / A. Sommerfeld // Ann. Phys. – 1909. – Vol. 333, Iss. 4. – P. 665–736.

• 6.    Ritchie R.H. Plasma Losses by Fast Electrons in Thin Films / R.H. Ritchie // Phys. Rev. – 1957. – Vol. 106, Iss. 5. – P. 874–881.

• 7.    Kretschmann, E. Radiative Decay of Non Radiative Surface Plasmons Excited by Light / E. Kretschmann, H. Raether // Zeitschrift für Naturforschung A. – 1968. – Vol. 23, Iss. 12. – P. 2135– 2136.

• 8.    Федянин, Д.Ю. Усиление поверхностных плазмон-поляритонов в наноразмерных волноводах: дис. … канд. физ.-мат. наук / Д.Ю. Федянин. – Долгопрудный, 2013. – 138 с.

• 9.    Hugall, J.T. Plasmonic cavity coupling / J.T. Hugall, A. Singh, N.F. van Hulst // ACS Photonics. – 2018. – Vol. 5, no. 1. – P. 43–53.

• 10.    Квантовая наноплазмоника: учебное пособие / Е.С. Андрианов, А.П. Виноградов, А.В. Дорофеенко и др. – Долгопрудный: Издательский дом «Интеллект», 2015. – 368 с.

• 11.    Корниенко, В.Н. Особенности многоволновой самосогласованной динамики ансамбля автогенераторов и поля в прямоугольной области / В.Н. Корниенко, А.П. Привезенцев // Радиотехника и электроника. – 2013. – Т. 58, № 7. – С. 691–698.

• 12.    Корниенко, В.Н. Возбуждение волн круглой мембраны ансамблем автогенераторов / В.Н. Корниенко, А.П. Привезенцев // Радиотехника и электроника. – 2010. – Т. 55, № 3. – С. 362– 368.

• 13.    Корниенко, В.Н. Формирование пространственно-временных структур в системе активная среда-волновое поле в области с полупрозрачной границей / В.Н. Корниенко, А.П. Привезен-цев // Радиотехника и электроника. – 2011. – Т. 56, № 4. – С. 417–422.

• 14.    Привезенцев, А.П. Теория колебаний: учеб. пособие / А.П. Привезенцев. – Челябинск: Челяб. гос. ун-т, 2007. – 111 с.

Поступила в редакцию 17 июля 2023 г.

Bulletin of the South Ural State University

Series “Mathematics. Mechanics. Physics”

2023, vol. 15, no. 3, pp. 79–88

THE MODELING OF SURFACE PLASMON POLARITONS EXCITATION IN A RECTANGULAR GOLD-BASED NANORESONATOR

• I .V. Bychkov, D.A. Kuzmin, M.A. Zagrebina

Received July 17, 2023