Моделирование взаимодействия фуллерита C60 с подложкой твердого тела

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2019PNRPU MECHANICS BULLETIN

Начало XXI века охарактеризовалось большим объемом теоретических и экспериментальных исследований в области наноматериалов и нанотехнологий, в том числе материалов и технологий, использующих такие аллотро-ные формы углерода, как фуллерен и фуллерит [1–11].

В работах [12, 13] приведен обзор различных форм углеродых соединений и их современное применение.

В работах [14–16] исследовалось взаимодействие с твердым телом как отдельного фуллерена, так и фуллеренового кластера. В данной работе будет исследоваться процесс взаимодействия фуллерита C 60 с подложкой твердого тела.

Фуллерены, являющиеся одной из аллотропных форм углерода, способны образовывать молекулярные кристаллы, называемые фуллеритами.

В работе [17] указаны основные свойства и параметры фуллеритов, в том числе и фуллерита C60:

• –    структура кристалла фуллерита может быть как гранецентрированной кубической, так и гексагональной, при этом гранецентрированная кубическая структура является предпочтительной;

• –    при температуре выше 259 К имеет место вращение молекул фуллеренов в узлах решетки фуллерита, при температуре ниже 259 К такое вращение отсутствует;

• –    постоянная кристаллической решетки при вращении молекул фуллеренов составляет (1,4154±0,0003) нм, при статическом положении фуллеренов (1,4111±0,0003) нм.

В работе [18] с помощью аппарата молекулярной динамики изучены механические и структурные свойства фуллерита различного состава.

Целью данной работы является моделирование процесса взаимодействия фуллерита C60 с подложкой твердого тела.

1. Постановка задачи

Подложка твердого тела моделировалась как кристалл железа Fe(100) с кубической объемно-центрированной кристаллической решеткой, постоянная решетки 2.87 Å [16]. Кристаллическая решетка фуллерита C 60 принята как гранецентрированная кубическая с постоянной, равной 1,4154 нм. Расчетная ячейка имеет периодические граничные условия.

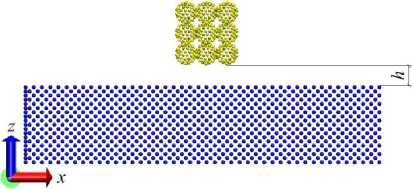
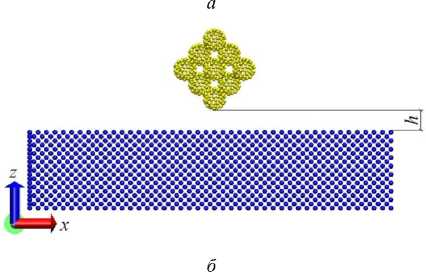
На рис. 1 изображена система «подложка–фуллерит C60» в начальный момент времени. Здесь рассматривалось три варианта ориентации фуллерита C60 по отношению к подложке – грань, ребро и вершина.

До момента соударения фуллерита С60 с подложкой твердого тела ему придавалась скорость, вектор которой был направлен по нормали к верхней грани кристалла железа, а модуль составлял соответственно 0,005, 0,01, 0,02 Å/фс. В таком случае кинетическая энергия каждого из фуллеренов, входящих в состав фуллерита, составит: при скорости 0,005 Å/фс – 0,93 эВ, при скорости 0,01 Å/фс – 3,73 эВ, при скорости 0,02 Å/фс – 14,94 эВ.

Равнодействующая сила определяется как

ur uur u  dU ( r^..., rN )  uex

F: =--+ F,

6 r

uur ex где U – потенциальная энергия системы; F – сила, определяемая взаимодействиями с молекулами среды [20].

Потенциал энергии системы представляет собой совокупность потенциалов различных видов взаимодействия [21]:

U ( r ) = U b + U _e+ U _ф+ U vw + U_qq ,         (3)

е

в

Рис. 1. Фуллерит С₆₀ и подложка железа: а – грань; б – ребро; в – вершина

где U – потенциал изменения длины связи; U – потенциал изменения угла между связями; U – потенциал изменения торсионного угла и плоских групп; U – потенциал Вандерваальсового взаимодействия; U – потенциал электростатического взаимодействия.

Математическая форма записи приведенных потенциалов приведена в работах [22–25, 28].

Потенциал химических связей определяется изменением длины связи между атомами (рис. 2). Вот некоторые из форм записи данного потенциала:

U b = E D b ( P y -P o ) ² , b

Ub = E D b ( p j -P o ) ², |p j -P o| ^P c ’ b

^Ub = E D b P ^{2 +} D rh P c (|p j -P o I ^-P c ) , |P j -P o I ^ P c , b

Fig. 1. Fullerite C₆₀ and iron substrate: a – face; b – edge; c – top

Расстояние h от верней грани подложки до фулле-рита С₆₀ составляла 11,5 Å.

После контакта фуллерита С 60 с кристаллом железа скорость, которая была ему придана, обнулялась.

В системе «подложка–фуллерит C60» моделировались следующие температуры: 300, 700, 1150 K.

Моделирование велось с шагом по времени A t = 1 фс.

Во всех проведенных компьютерных экспериментах продолжительность моделируемого процесса t м = 30 пс.

Описание метода молекулярной динамики и потенциалов взаимодействия между исследуемыми элементами приведено в работах [20–25, 28].

Суть метода молекулярной динамики состоит в том, что для моделирования поведения многоатомной молекулярной системы используется классическое уравнение движения, имеющее вид [20]

m

d2 u( t) = u dt2        '

где i – номер атома; N – полное число атомов в системе; ur                                         uur mi – масса атома; r – радиус-вектор атома; F – равнодействующая сил, действующих на атом.

где b - количество химических связей; D_b, D_rh - константы; p₀ - значение равновесной длины связи; p^ -значение текущей длины связи; p_c - значение критической длины связи.

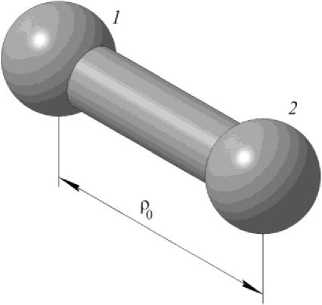
Рис. 2. Длина связи между атомами 1 и 2 в равновесном состоянии

Fig. 2. The bond length between atoms 1 and 2 in equilibrium

Потенциал валентного угла характеризуется изменением угла между связями атомов (рис. 3) и определяется соотношением, аналогичным (4):

U b = Z D ₉( 6-6 o ) 2 , a

Электростатическое взаимодействие определяется кулоновским потенциалом:

где a – количество валентных углов; D – константа;

9₀ - значение равновесного валентного угла; 0 . - значение текущего валентного угла.

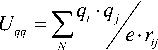
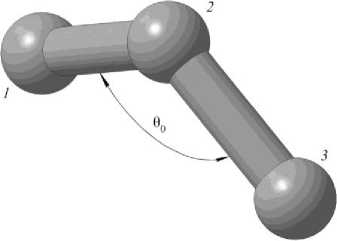
Рис. 3. Угол между связями атомов 1 , 2 и 3 в равновесном состоянии

Fig. 3. The angle between the bonds of atoms 1 , 2 and 3 in equilibrium

Потенциал изменения торсионного угла и плоских

групп, изображенного на рис. 4, имеет вид

Ub = Z d

<

D _ф( cos ( n ф-ф ₀ ) + 1 ) , n * 0,

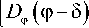
, n = 0,

где d - число двугранных углов; D _ф - константа, определяющая высоту потенциальных барьеров двугранных углов ф ; ф₀ - сдвиг фазы; n - кратность торсионного барьера.

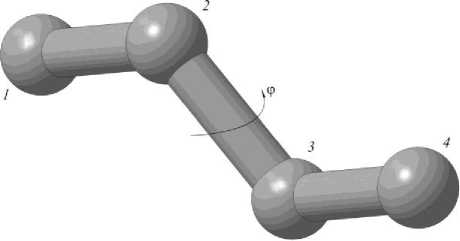
Рис. 4. Изменение торсионного угла ф между атомами 1 , 2 , 3 и 4

Fig. 4. Change in the torsion angle ф between atoms 1 , 2 , 3 and 4

Вандерваальсовые взаимодействия атомов описываются с помощью потенциалов Леннарда–Джонса:

Uvw = 4^(^ - Г/) ,             (8)

где Z - глубина потенциальной ямы; r = Rj / p₀ - приведенное межатомное расстояние; R – вектор, соединяющий центры атомов i и j .

где q_i, q j – парциальные заряды атомов; e – диэлектрическая проницаемость среды.

При моделировании использовались следующие потенциалы: изменения длины связи (4), изменения угла между связями (6), изменения торсионного угла и плоских групп (7). Взаимодействие между атомами кристаллической решетки железа описывалось Вандерва-альсовым взаимодействием (8). Связи между атомами углерода и атомами железа не устанавливаются, а взаимодействие «железо–углерод» описывалось потенциалом в форме Леннарда–Джонса (8).

Осаждением фуллерена C 60 на подложке железа считается наличие контакта между фуллереном и подложкой к 30 пс, т.е. к моменту окончания компьютерного эксперимента.

Для реализации компьютерных экспериментов по исследованию взаимодействия фуллерита C60 с подложкой твердого тела в соответствии с описанным выше методом молекулярной динамики использовался программный комплекс LAMMPS [29–32]. Программный комплекс LAMMPS используется для моделирования различных процессов на молекулярно-динамическом уровне [33–36]. При моделировании процесса в LAMMPS использовалось силовое поле CHARMM [37] (Chemistry at HARvard Macromolecular Mechanics), значение констант потенциалов, определяемое полем CHARMM, также содержится в этом программном комплексе.

2. Результаты расчетов системы «подложка железа – фуллерит C60»

Результаты моделирования процессов взаимодействия фуллерита C 60 с подложкой железа приведены в табл. 1. Из табл. 1 следует, что в компьютерных экспериментах наблюдалось как осаждение всех фуллеренов C 60 , контактировавших с подложкой, так и частичное их осаждение, в одном из случаев ни один из фуллеренов C₆₀, образовавших фуллерит, не осел на подложке.

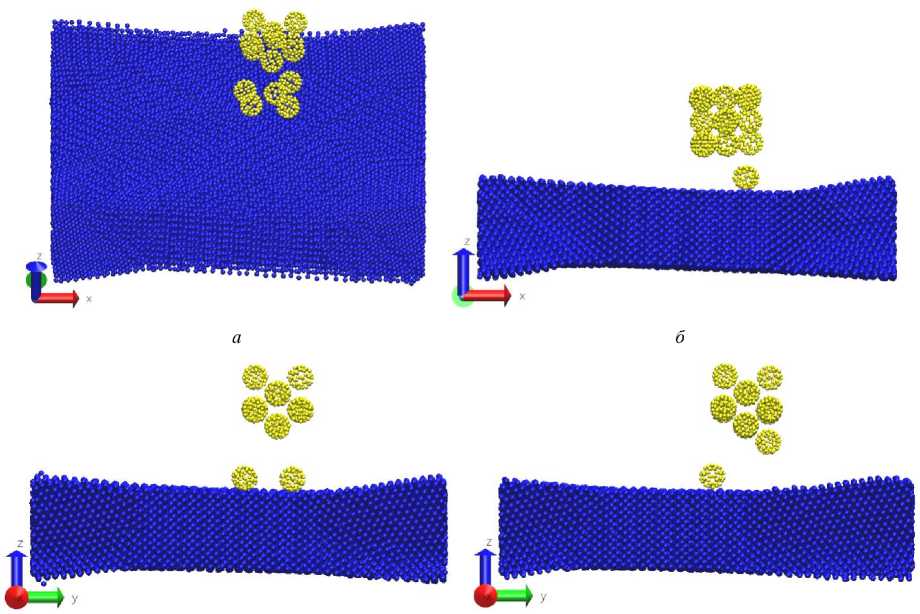
На рис. 5 показаны результаты осаждения фуллери-та C 60 на подложку на 30 пс.

В случаях ориентации фуллерита C60 гранью относительно подложки собственно грань фуллерита контактирующую с подложкой железа Fe (100) назовем первым слоем. Для однозначности описания поведения фуллеренов первого слоя фуллерита C60, осевших на контактной поверхности подложки, пронумеруем их, как показано на рис. 6.

При соударении фуллерита C₆₀, ориентированного гранью относительно подложки, на скоростях v = = 0,005…0,01 Å/фс все фуллерены первого слоя оседают на подложке.

Таблица 1

Количество фуллеренов осевших на кристалле железа после соударения

д

Рис. 5. Осаждение фуллерита С₆₀ с подложкой железа: а – грань, v = 0,01 Å/фс, T = 1150 K; б – грань, v = 0,02 Å/фс, T = 1150 K; в – ребро, v = 0,01 Å/фс, T = 1150 K; г – ребро, v = 0,02 Å/фс, T = 1150 K; д – вершина, v = 0,01 Å/фс, T = 1150 K; е – вершина, v = 0,02 Å/фс, T = 1150 K

е

Table 1

The number of fullerenes deposited on the iron crystal after the collision

Скорость фуллерита v , Å/фс		0,005			0,01			0,02
Температура системы подложка и фуллерит C 60 , K		300	700	1150	300	700	1150	300	700	1150
Ориентация фуллерита C 60 относительно кристалла железа	грань	5	5	5	5	5	5	4	2	1
	ребро	2	2	2	2	2	2	2	1	1
	вершина	1	1	1	1	1	1	1	1	–

Fig. 5. Deposition of fullerite C₆₀ with an iron substrate: а – face, v = 0.01 Å/fs, T = 1150 K; b – face, v = 0.02 Å/fs, T = 1150 K; c – edge, v = 0.01 Å/fs, T = 1150 K; d – edge, v = 0.02 Å/fs, T = 1150 K; e – top, v = 0.01 Å/fs, T = 1150 K; f – top, v = 0.02 Å/fs, T = 1150 K

Приведенные результаты компьютерного эксперимента коррелируют с результатами натурного эксперимента, приведенного в работе [38], где исследовался процесс адсорбции нейтральных молекул фуллеренов при температуре 600–650 K, c кинетической энергией 0,01– 3 эВ, на поверхности различных твердых тел (Al, Ni, Si, MgO, SrTiO 3 ). Результатом эксперимента [38] является получение пленки C₆₀ диаметром около 7 мм.

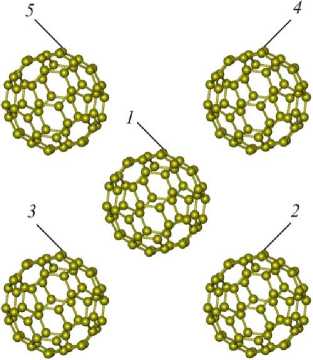
Рис. 6. Нумерация фуллеренов первого слоя фуллерита С60

• Fig. 6.    Numbering of fullerenes of the first layer of fullerite C₆₀

При скорости фуллерита C 60 , равной 0,02 Å/фс, и кинетической энергии фуллеренов, входящих в его состав, равной 14,94 эВ, с увеличением температуры от 300 до 1150 K число осевших на кристалле железа фуллеренов уменьшается. Столь резкое изменение в поведении фуллеренов после контакта с подложкой железа может отражать факт превышения предела кинетической энергии фуллеренов, при котором взаимодействие «железо – углерод» может быть описано потенциалом в форме Леннарда–Джонса, что требует дополнительных исследований.

В табл. 2 показаны максимальные изменения расстояний от первоначальных, в процентах, между центральным фуллереном 1 и периферийными 2–5 , при различных условиях. Расстояние между фуллеренами измерялось как расстояние между центрами масс фуллеренов. Отрицательное значение изменения в табл. 2 означает, что расстояние между центральным фуллереном и периферийным уменьшилось, а положительное значение изменения означает, что расстояние увеличилось. На рис. 7 представлен график изменения расстояния между центральным фуллереном в осевшей на подложке грани и периферийными в зависимости от времени.

Из графика на рис. 7 следует, что до удара фуллери-та C60 о подложку расстояние между фуллеренами первого слоя квазилинейно уменьшается на величину порядка 1,5 %. После соударения изменение расстояний между центральным и периферийными фуллеренами первого слоя носит разнонаправленный характер, одна- ко с течением времени амплитуды изменений расстояний уменьшаются, и к 30 пс наступает квазистационар-ное состояние.

Таблица 2

Изменения расстояний между центральным и периферийными фуллеренами 1-го слоя

Changes in the distance between the central and peripheral fullerenes of the 1-st layer

Table 2

Скорость фуллерита v , Å/фс		0,005			0,01
Температура системы подложка и фул-лерит C 60 , K		300	700	1150	300	700	1150
Изменение расстояния между центральным фуллереном 1 и периферийными 2 , 3 , 4 , 5 , %	1–2	- 4, 45	- 4,57	- 7, 02	- 5,88	- 5,88	- 4, 44
		6,82	4,45	8,15	9,51	9,51	7,05
	1–3	- 5,85 3,92	- 5,12 4,67	- 4,56 7,43	- 5, 61 6,94	- 5, 61 6,94	- 3, 73 3,49
	1–4	- 4,59 4,68	- 5, 21 10,77	- 4,88 11,90	- 5, 05 11,02	- 5, 05 11,02	- 5,54 2,58
	1–5	- 3,17 3,89	- 4,59 9,96	- 3.70 3,76	- 5,19 5,49	- 5,19 5,49	- 4,60 14, 72

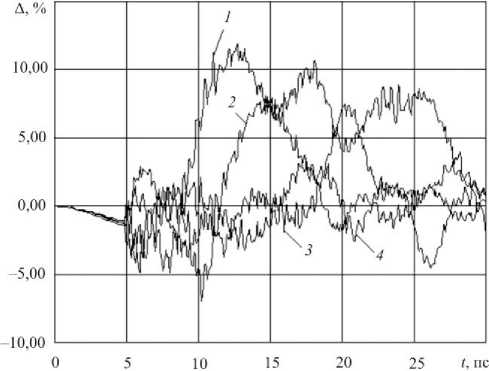
Рис. 7. Изменение расстояния между центральным фуллереном и периферийными в плоскости xOy при T = 1150 K, v = 0,005 Å/фс: (1) – 1 – 2; (2) – 1 – 3; (3) – 1 – 4; (4) – 1 – 5

• Fig. 7.    Change distance between central fullerene and peripheral in the x O y plane at T = 1150 K, v = 0,005 Å/fs: ( 1 ) – 1 – 2;

( 2 ) – 1 – 3; ( 3 ) – 1 – 4; ( 4 ) – 1 – 5

Осаждение фуллеренов C 60 , образующих фуллерит, наблюдается и в случае если фуллерит при соударении с подложкой был ориентирован к ней ребром. В табл. 3 показаны максимальные (уменьшение и увеличение) изменения от первоначального расстояния между фуллеренами ребра фуллерита при различных условиях. Содержание положительного и отрицательного значения изменения расстояния между фуллеренами аналогично приведенному в табл. 2. На рис. 8 и 9 представлены графики изменения расстояния между осевшими на подложке фуллеренами в зависимости от времени.

Таблица 3

Изменения расстояния между фуллеренами грани

Table 3

Changes in the distance between the fullerenes of the face

Скорость фуллерита, Å/фс	0,005			0,01			0,02
Температура системы подложка и фуллерит C60, K	300	700	1150	300	700	1150	300
Изменение расстояния между фуллереном грани, %	- 32,76	- 31,53	- 5,62	- 33, 28	- 31, 21	- 7,38	- 31,18
	0,00	0,00	11,16	0,00	0,00	4,41	5,95

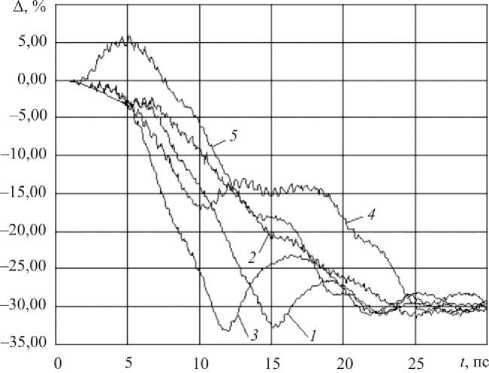
Рис. 8. Изменение расстояния между фуллеренами «ребра»: ( 1 ) T = 300 K, v = 0.005 Å/фс; ( 2 ) T = 700 K, v = 0,005 Å/фс; ( 3 ) T = 300 K, v = 0,01 Å/фс; ( 4 ) T = 700 K, v = 0,01 Å/фс;

( 5 ) T = 300 K, v = 0,02 Å/фс

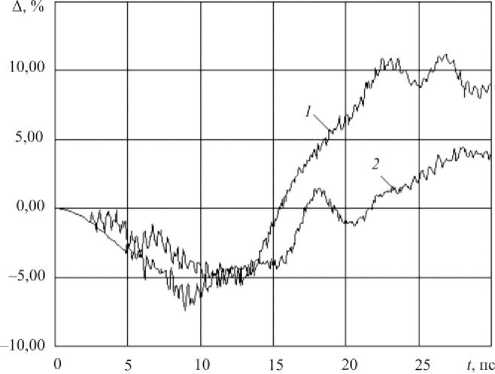
Рис. 9. Изменение расстояния между фуллеренами ребра при T =1150 К: ( 1 ) v = 0,005 Å/фс; ( 2 ) v = 0,01 Å/фс

Fig. 9. The change in the distance between the fullerenes of the rib at T = 1150 K: ( 1 ) v = 0,005 Å/фс; ( 2 ) v = 0,01 Å/фс

• Fig. 8.    Changing the distance between the fullerenes of «edge»: ( 1 ) T = 300 K, v = 0.005 Å/фс; ( 2 ) T = 700 K, v = 0.005 Å/фс; ( 3 ) T = 300 K, v = 0.01 Å/фс; ( 4 ) T = 700 K, v = 0.01 Å/фс;

• ( 5 ) T = 300 K, v = 0.02 Å/фс

Из графиков на рис. 8 следует, что при температурах системы 300, 700 K расстояние между осевшими фуллеренами сокращается на 30 %. При этом если в интервале 5–15 пс изменение расстояния между фуллеренами может носить разнонаправленный характер, то к 25 пс наступает квазистационарный режим и расстояние между осевшими фуллеренами существенно не изменяется.

На рис. 9 представлены графики изменения расстояния между фуллеренами, осевшими на подложке при T = 1150 К. В обоих случаях первоначально наблюдается уменьшение расстояния между фуллеренами, а затем оно начинает увеличиваться и к 30 пс превышает расстояние между фуллеренами фуллерита C₆₀.

Проведенное моделирование позволило установить основные закономерности процесса взаимодействия фуллерита C60 с подложкой твердого тела, которой являлся кристалл железа Fe(100).

Выводы

• 1.    С увеличением скорости фуллерита C₆₀ относительно подложки твердого тела количество фуллеренов, осаждающихся на подложке, уменьшается.

• 2.    При ориентации фуллерита C₆₀ гранью относительно кристалла железа расстояние между осевшими фуллеренами (центральный – периферийные) изменяется в пределах от –8 до 15 %.

• 3.    При соударении фуллерита C 60 ребром о подложку при температурах системы 300, 700 K расстояние между осевшими фуллеренами сокращается на 30 %, и с 25 пс фуллерены C₆₀, осевшие на подложке железа, занимают квазистационарное положение, а при температуре 1150 К наблюдается увеличение расстояния между осевшими фуллеренами.

• 4.    Контакт фуллерита C 60 вершиной о подложку приводит к осаждению фуллерена, находящегося в вершине фуллерита, во всех диапазонах моделируемых условий, кроме случая с параметрами взаимодействия v = 0,02 Å/фс, T = 1150 K.