Моделирование задачи о вынужденных колебаниях плотины-пластинки с постоянной и переменной толщины при действии сейсмической нагрузки

Рассматривается задача о вынужденных колебаниях плотины-пластинки с постоянной и переменной толщины при действии сейсмической нагрузки. Плотину рассматриваем как пластинку постоянной и переменной толщины, с учетом поперечной сейсмической нагрузки и давления воды. На плотину- пластинку будут действовать следующие силы: -силы инерции, возникающие от движения плотины и ее деформации; -гидродинамическое давления воды. На основе гипотезы Кирхгофа-Лява выводятся уравнения колебаний плотины-пластины с учетом вязкоупругих свойств материала. Математическая модель задачи, относительно поперечного прогиба w1 = w1 (x,y,t), при известных допущениях [1-3] с учетом вязкоупругих свойств материала плотины-пластинки сводится к решению уравнений вида

-(1 - Д') D V 4 w, + 2 — — V2 w, + 2 — — V 2 w, + V 2 D V 2 w, -hv      v|_       1     dy Sy     1     dz Sz     1            1

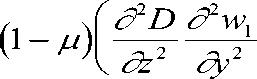
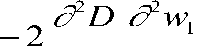
dzdy dzdy

+

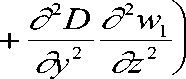
⁺ P 1

^d ( ^w 1 ^{+ w} 0 ) a ²

—

— cos а h

dP1 dt

P p P о   1

h I dt   2

+

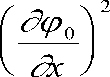
r

V

x = ytga

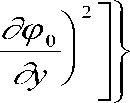
cos a = 0

x = ytga + w °

( t )

где w1 (x,y,t) — прогиб плотины-пластинки; h - толщина плотины- пластинки; pi - плотность материала плотины; р - плотность воды; ф(x,y,z,t)

- функция потенциала скоростей движения жидкости, возникающего от деформации плотины-пластинки; ф0(x,y,t)- функция потенциала скоростей движения жидкости, возникающего от движения плотины как твердого тела;

w ₀ ( t ) - закон движения основания при землетрясении:

w0 (t) = a0 e E°t sin to 01;

здесь a0 -начальная максимальная амплитуда; £0 -коэффициент затухания грунта; to0 -частота колебания грунта; t -время. Все эти величины определяются из анализа сейсмограммы соответствующего балла землетрясения.

Система уравнений (1) является достаточно общей. Из нее в частном случае можно получить уравнения колебаний плотины-пластинки постоянной и переменной толщины с учетом вязкоупругих свойств материала.

Решение интегродифференциальных уравнений (1), удовлетворяющее граничным условиям задачи, задаем в виде то wi (У, z, t ) =      Ck ( t ) wk (У, z), k = 1,3,...

где Ck = Ck (t) -искомые функции времени; координатные функции wk (y,z) удовлетворяют граничным условиям закрепления краев плотины - пластинки.

Исследование таких уравнений с помощью метода Бубнова-Галеркина, основанного на многочленной аппроксимации прогиба, сводится к решению систем интегродифференциальных уравнений в обычных производных типа Вольтерра:

то

k = 1 , 3 ,...

В расчетах использовано трехпараметровое ядро Колтунова-Ржаницына:

R(t) = At1,1 e^p(-pt),    A,р>0,    0<а< 1.

Интегрирование системы уравнений (2), полученное на основе многочисленной аппроксимации прогибов, выполнено с помощью численного метода, основанного на использовании квадратурных формул [4]. На основе этого метода разработан эффективный вычислительный алгоритм решения задач динамики плотины-пластины с постоянной и переменной жесткостью с. учетом вязкоупругих свойств материала. На рис.1 и рис.2 приведены графики кривых для различных значений реологического параметра А. Из этих результатов видно влияние вязкоупругих свойств материала плотины - пластины. Решения упругой и вязкоупругой задачи в начальный период времени мало отличаются друг от друга. С течением времени вязкоупругие свойства оказывают существенное влияние, что приводит к заметному отличию решений. Заметим также, что с увеличением параметра А амплитуда колебаний уменьшается. Наблюдения показывают, что с увеличением коэффициента А частота колебаний также уменьшается.

Кроме того в работе изучены влияния других свойств и параметров плотины и воды при сейсмических нагрузках. Подробно изучены влияния этих параметров на напряженно-деформированное состояние плотины-пластины.

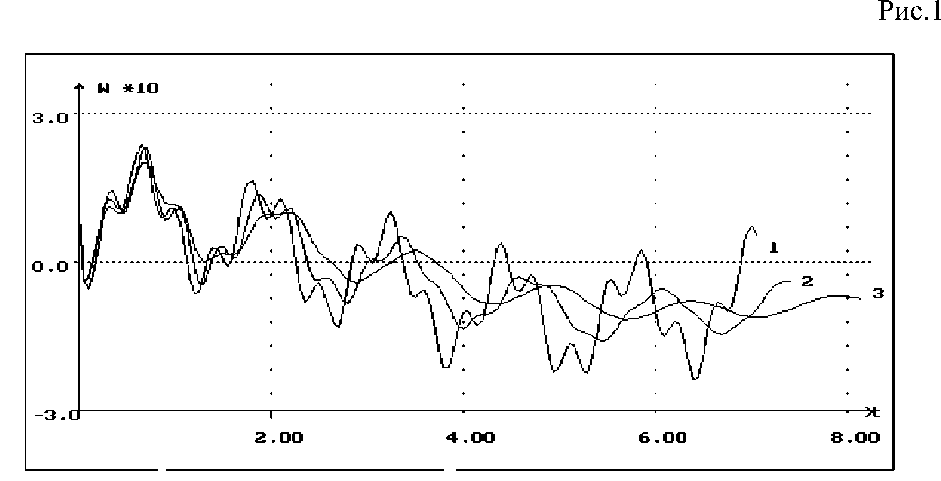
Рис.2

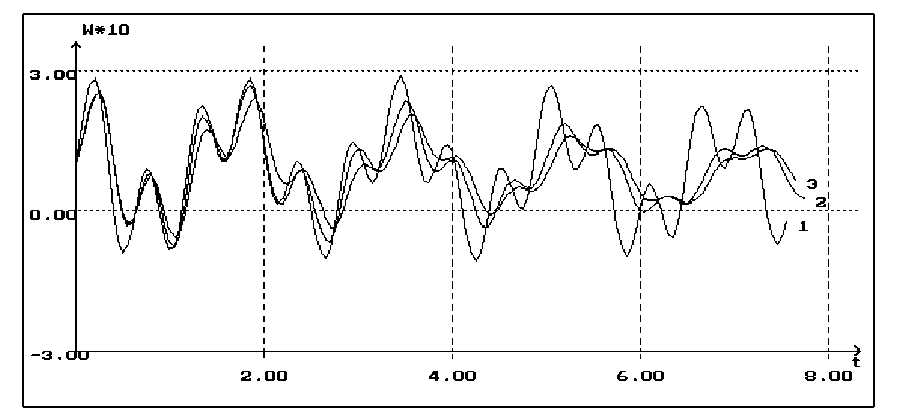
Влияние вязкоупругого свойства материала плотины-пластины постоянной толщины

Рис.2. Плотины-пластины переменной толщины при различных значениях реологического параметра А:   0(1);   0,05(2);   0,1(3).