Моделирование заделки корней саженцев катками при посадке леса
Бесплатный доступ
Исследование посвящено эффективности уплотнения почвы вокруг корней высаживаемых растений катками лесопосадочной машины. Представлены графическая и аналитическая модели процесса воздействия катков на почву в области размещения корней. Разработана методика определения размеров уплотненного и неуплотненного слоев почвы по глубине, а также колеи, остающейся от катка. Даны рекомендации по установке катков и глубине размещения корней растений
Посадка леса, катки, почва, корневая система, область напряжений, колея
Короткий адрес: https://sciup.org/147112185
IDR: 147112185
Текст научной статьи Моделирование заделки корней саженцев катками при посадке леса
Посадка леса является наиболее эффективным способом его искусственного восстановления на вырубаемых площадях, а также при лесоразведении, создании лесозащитных полос и пр. [1]. На открытых площадях и вырубках после корчевки пней широко применяются машины для непрерывной посадки леса с рабочими органами в виде катков для заделки корней высаживаемых растений (культур). В соответствии с требованиями к посадке катки должны обеспечивать плотную заделку корневых систем на всей глубине их расположения, не допуская при этом значительных повреждений [2].
Чтобы приблизиться к выполнению этого требования, следует направить векторы давления от обода на почву в сторону корней, поэтому рабочую поверхность катка устанавливают под некоторым углом, а величина силы N , приложенной к катку, должна обеспечить необходимую степень уплотнения почвы.
На рисунке представлена схема цилиндрического катка при неполном погружении его обода шириной B на некоторую глубину p в почву.
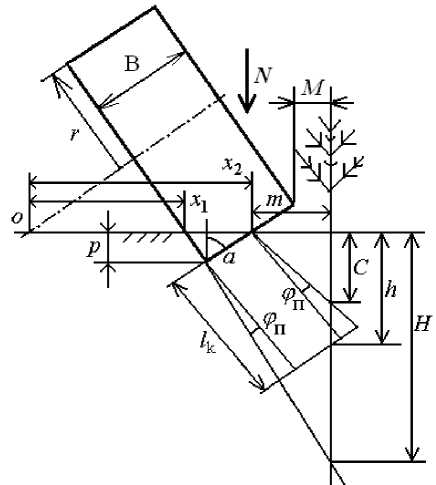
Рис.
Область напряжений, вызванных катком в почве, представляет в поперечном сечении трапецию, боковые стороны которой расположены под углами ф п внутреннего трения от нормали к ободу, а размер верхнего основания равен длине части ширины обода, погруженной в почву.
Высота l k области напряжений определяется по формуле [3]:
l k =
B --+ п fп
( B
V I П fп V
N sin а [ ^ 1 п f п2
1 Автор – профессор кафедры технологии и оборудования лесного комплекса
где f – коэффициент внутреннего трения; п а _ угол между поверхностью обода и вертикалью; [^] - удельное сопротивление почвы смятию.
Расстояние C от поверхности почвы до начала области воздействия катка на стержневой корень (минимальная глубина заделки) определяется так:
C = m • tg ( а - Ф п ) , (2)
где m – расстояние от растения до ближайшей точки пересечения катка с поверхностью почвы. Заметим, что при полном погружении обода в почву величина m соответствует расстоянию M между внутренним ребром катка и осью растения.
Максимальная глубина h заделки стержневого корня определяется так:
, lk _ M • cos2 a h = p +— --B • cosa--. (3)
sin a sin a
В теории [4] границу воздействия на объект в почве определяют по точке пересечения граничного вектора области напряжений с этим объектом. Согласно этому представлению, максимальная глубина H заделки корней определяется только геометрически, с учетом угла внутреннего трения в почве. Реально эта глубина ограничена величиной h (см. рис.). Несоответствие между реальной и представляемой величинами глубины заделки при выборе параметров катков приводит к образованию пустот на глубине H — h вокруг корня и снижению приживаемости растений.
После преобразований выражения (6) с учетом (7), получим:
x 2
S = ( cos a ) ^ J V к 2 — x 2 dx . (8)
x 1
Решение интеграла (7) имеет вид [6]:
S = ( cos a ) •
x • T - 2
k
x 2 k 2
1 arcsin 2
x к
x 2
x 1
В окончательном виде решение задачи определения площади пятна контакта катка с почвой выглядит так:
Пятно контакта катка с поверхностью почвы представляет собой фрагмент эллипса. Допустим, что каток имеет контакт с почвой только частью, расположенной впереди его диаметральной плоскости по ходу движения машины, а остальная часть располагается выше уровня дна образуемой колеи. Заметим, что это допущение не учитывает упругую деформацию почвы под катком. В этом случае пятно контакта занимает часть в одной четверти полного эллипса, т. к. в условиях эксплуатации каток не погружается в почву выше своей оси. Определим площадь S пятна контакта при известной величине p погружения катка в почву.
S = cos a = 2
пк2 ,2 • L 2p к к arcsinl 1---— I —
2 k к • sin2 a j
[ , 2 p ) 4 кр 4 p
— к• k sin 2a j Vsin2a sin2 2a
Уравнение эллипса имеет вид [5]:
x 2
k 2
+ yr = 1
b 2 ,
где k и b – соответственно большая и малая полуоси эллипса. Из рис. следует:
r к =-----; b = r.
cos a
Подставив эти значения в (4), получим уравнение:
П 2 2
y = rr — x cos a .
С учетом вышеизложенного, площадь S пятна контакта определится так:
x 2
S = [ Vr2 — x2 • cos2 a dx, x1
Максимальное значение S определяется по элементарной формуле:
N
S = — . (10)
[ ^ ]
Пример: Ширина обода заделывающего катка 0,1 м; расстояние от внутреннего ребра катка до оси растения (защитная зона) составляет 0,025 м; угол наклона обода к вертикали 72º; радиус катка 0,23 м; часть веса машины (вертикальная сила), приложенная к одному катку, составляет 1900 Н; удельное сопротивление почвы смятию 108 кПа; коэффициент внутреннего трения в почве 0,37. Требуется определить глубину погружения катка в почву, а также диапазон глубины, в котором происходит уплотнение почвы по оси высаживаемых растений.
Решение:
1) Определим максимальное значение величины S пользуясь выражением (10):
108 • 10 3
= 0,0176 м2.
2) Определим высоту области напряжений под ободом катка из выражения (1):
l k = —
0,1 +
3,14 • 0,37
где x 2 и x 1 – координаты точек пересечения катка с почвой, соответственно ближней и отдаленной от растения (см. рис.)
( 0,1 к 2 1900 • sin 72 0
+ I I +
\к3,14 • 0,37 7 108 • 10 3 • 3,14 • 0,37 2
x 1 = к-p —; x 2 = к ; к = —r— . (7)
sin 2 a cos a
= 0,1292 м.
3) Из выражения (7) определим значение k :
k = 0,23 = 0,7443 м.
cos720
-
4) Подставляя в выражение (9) вычисленные величины S и k , решим полученное уравнение с одним неизвестным p . При использовании для решения метода последовательного приближения рекоменду-
- ется первое значение p1 принять 0,1 м. Получим:
p = 0,07 м.
-
5) Определим из выражения (3) максимальное значение глубины уплотнения почвы по оси растений:
h = 0,07 + 0,1292 - 0,1 • cos 72 0 - sin720
0,025 • cos2 720 sin 720
= 0,1724 м.
-
6) Определим величину m для подстановки в выражение (2). Длина B 1 касательной к ободу в части его, погруженной в почву (при отсчете от внешнего ребра катка в сторону растения), определится так:
B 1 = = 0,07 = 0,2265 м; B 1 > B .
cos a cos72u
Следовательно, обод на уровне дна колеи полностью погружен в почву, в этом случае m = M .
-
7) Из выражения (2) определим минимальную глубину C заделки корня:
C = 0,025 • tg ( 72 0 - arctg0,37 ) = 0,0316 м.
Ответ: Глубина колеи от катка составляет 0,07 м; диапазон глубины уплотнения почвы по оси высаживаемых растений 0,03 – 0,17 м.
Использование результатов расчетов по предлагаемым моделям на практике
Численные данные при решении примера заимствованы из характеристики лесопосадочной машины типа СШН-3 при работе по вспаханной супесчаной почве [4]. Такая машина может высаживать растения с длиной корневой части до 0,25 м, если ориентироваться на возможность ее сошника готовить борозду соответствующей глубины.
Результаты выполненных расчетов показывают, что уплотнение почвы будет осуществляться только до глубины 0,17 м, что ограничивает и длину корней. Начало глубины уплотнения с 0,03 м требует соответствующего опускания корневой шейки ниже поверхности почвы, таким образом, допустимая длина корней по требованию к их уплотнению сокращается до 0,14 м.
Образование колей от катков по обе стороны оси размещения растений достигает глубины 0,07 м, что может создать неблагоприятный водно-воздушный режим для развития растений. В конструкции машины СШН-3 предусмотрена установка загортачей после катков. Ими надо обязательно воспользоваться для закрытия колей, при этом первоначальную установку произвести на глубину около 0,07 м.
При увеличении силы, действующей на катки, с целью увеличить глубину уплотнения почвы следует соблюдать осторожность, т. к. величина напряжения в почве под действием катков возрастает пропорционально второй степени по мере приближения к ободу. Так, если на расстоянии 0,13 м от катка в почве создается напряжение 108 кПа, т. е. до исходной величины, то, например, на расстоянии 0,065 м это напряжение составляет 0,43 МПа. На расстоянии 0,013 м величина напряжения в почве составляет 11 МПа, что чревато повреждением поверхности корней, если увеличить упомянутую выше силу.
ВЫВОДЫ
-
1. Глубина уплотнения почвы катками вокруг корней растений ограничивается не только силой, действующей на каток, но также длиной области напряжений в почве.
-
2. Разработаны графические и аналитические модели, которые позволяют определить параметры воздействия катков лесопосадочных машин на почву и высаживаемые растения.
-
3. Погрешности моделей связаны только с точностью определения элементарных механических характеристик почвы – ее удельного сопротивления смятию и коэффициента внутреннего трения.
Список литературы Моделирование заделки корней саженцев катками при посадке леса
- Родин А. Р. Лесные культуры и лесомелиорация: Учебник для вузов/А. Р. Родин. М.: Лесн. пром-сть, 1979. 328 с.
- Винокуров В. Н. Машины и механизмы лесного хозяйства и садово-паркового строительства: Учебник для вузов/В. Н. Винокуров, Г. В. Силаев, А. А. Золотаревский. М.: Изд. центр «Академия», 2004. 320 с.
- Цыпук А. М. Повышение эффективности лесовосстановительных работ ресурсосберегающей технологией: Дис. … докт. техн. наук/А. М. Цыпук. Петрозаводск, 1996. 299 с.
- Зима И. М. Механизация лесохозяйственных работ: Учебник для вузов/И. М. Зима, Т. Т. Малюгин. М.: Лесн. пром-сть, 1976. 416 с.
- Зак Г. Г. Справочник конструктора/Г. Г. Зак, Л. И. Рубинштейн. Минск: Изд-во АН БССР, 1963. 567 с.
- Бермант А. Ф. Краткий курс математического анализа: Учебник для вузов/А. Ф. Бермант, И. Г. Арманович. М.: Наука, 1967. 608 с.
- Двайт Г. Б. Таблицы интегралов и другие математические формулы/Г. Б. Двайт. М.: Наука, 1978. 228 с.


