Моделирование зависимости характера разрушения образца от коэффициента жесткости напряженного состояния у вершины трещины

Лицензировано по CC BY 4.0. Чтобы ознакомиться с условиями этой лицензии, перейдите по ссылке сти напряженного состояния у вершины трещины // Вестник Пермского университета. Математика. Механика. Информатика. 2025. № 4(71). С. 46–59. DOI: 10.17072/1993-0550-2025-4-46-59.

Механика разрушения конструкционных материалов прошла значительный путь развития – от классических энергетических концепций к современным численным моделям, учитывающим сложное деформированное состояние в окрестности дефектов.

Развитие механики разрушения как самостоятельной научной дисциплины началось в середине XX века с работ, направленных на описание критических условий роста трещин в твердых телах. Одним из основополагающих этапов стало формулирование принципов линейной механики разрушения, в рамках которой были введены такие ключевые параметры, как энергетический критерий Гриффитса [1], коэффициент интенсив- ности напряжений K [2]. Применение механики разрушения вошло в инженерную практику оценок трещиностойкости объекта под нагрузкой. Развитие нелинейной механики разрушения было основано на применении J-интеграла. В дальнейшем развитие получила нелинейная механика разрушения, включающая J-интеграл c целью исследования свойств концентрации пластических деформаций в окрестности вершины трещины [3, 4] и концепцию стеснения деформации, существенно влияющую на устойчивость материала к трещине [3].

Важным направлением в изучении предельных состояний материалов является разработка критериев разрушения, учитывающих жесткость напряженно-деформированного состояния. При этом для описания как хрупкого, так и вязкого разрушения эффективно используются критерии на основе напряжений. Хрупкое разрушение традиционно связывают с достижением критического нормального напряжения, в то время как вязкое (пластическое) разрушение, включающее стадию значительной пластической деформации, также может быть адекватно описано критерием на основе напряжений [5—7]. Это обусловлено тем, что дислокационные процессы, происходящие в зоне предразрушения, предшествующие квазихрупкому разрушению, зависят от локального напряженного состояния, в частности, от уровня гидростатического напряжения и интенсивности касательных напряжений.

Однако с течением времени стало очевидно, что однопараметрические модели не всегда адекватно отражают реальное поведение материалов, особенно при сложных схемах нагружения и геометрии трещины. Это стимулировало развитие двухпараметрических подходов, учитывающих помимо K или J, также несингулярные компоненты напряженного состояния, в частности T-напряжение и параметры трехосного стеснения, такие как Q-параметр, параметр трехосности h [8-11].

На современном этапе активно развиваются направления, связанные с анализом пространственного распределения напряженного состояния вблизи фронта трещины, особенно в трехмерной постановке. В этом контексте особый интерес представляет коэффициент жесткости напряженного состояния, отражающий локальную реакцию материала на внешние воздействия и зависящий от параметров НДС.

Коэффициент жесткости напряженного состояния П у вершины трещины представляет собой важную характеристику, отражающую соотношение между компонентами напряжений и определяющую тип локального деформирования - от плоского напряженного состояния до объемного. Исследования показывают, что распределение коэффициента жесткости вдоль фронта трещины может существенно влиять на характер разрушения - от хрупкого до вязкого. В работе [12] показано, что уровень локальной триакси-альности напряжений (например, через T-напряжение, Q-параметр и другие характеристики) определяет, насколько материал склонен к хрупкому разрушению при наличии трещины.

Установлено, что при высоком стеснении (например, в толстых телах или при би-аксиальном нагружении) снижается способность материала к пластической релаксации, и разрушение происходит более хрупко [13, 14].

Современные исследования демонстрируют перспективность использования данного параметра для описания вязко-хрупкого перехода [15-17].

Таким образом, изучение влияния коэффициента жесткости напряженного состояния на характер разрушения представляет собой актуальное научное направление, способствующее более точному описанию предельных состояний и надежности конструкционных материалов. Это особенно важно в контексте проектирования элементов, работающих в условиях сложного нагружения, где локальное поведение материала может существенно отличаться от среднестатистических характеристик.

Несмотря на значительное количество исследований, направленных на изучение влияния коэффициента интенсивности напряжений, J-интеграла и других параметров, вопрос о роли жесткости НДС в формировании траектории, скорости и формы зоны разрушения остается недостаточно раскрытым.

Однако, несмотря на значительный теоретический прогресс, остается недостаточно изученным количественное влияние схемы нагружения на распределение параметра P в окрестности вершины трещины и его связь с критическими условиями хрупкого разрушения при низких температурах.

Актуальность данной работы также обусловлена необходимостью более глубокого понимания взаимосвязи между локальными механическими условиями и макроскопическим сценарием разрушения, что имеет большое значение при проектировании конструкций, работающих в условиях сложного нагружения, в том числе динамического, циклического и ударного характера.

Таким образом, целью настоящей работы является разработка алгоритма оценки распределения коэффициента жесткости вдоль фронта трещины и в формировании подхода к прогнозированию характера разрушения материала на основе параметров напряженного состояния, включая радиус зоны пластичности и значения Т-напряжений.

Критерий вязко-хрупкого перехода на основе распределения коэффициента жесткости

Предлагаемый в настоящей работе критерий вязко-хрупкого перехода основан на анализе распределения коэффициента жесткости П вдоль фронта трещины. При этом расчет проводится в точке, соответствующей границе зоны пластичности вдоль линии продолжения трещины. Таким образом, формулируется следующая гипотеза: высокие значения коэффициента жесткости напряженного состояния П в зоне предразрушения вблизи границы пластической области обусловливают преобладание механизма хрупкого разрушения, характеризующегося зарождением и развитием микродефектов с образованием микротрещин. В данном случае распространение магистральной трещины происходит посредством слияния предсуществующих микротрещин. Напротив, при низких значениях параметра П в указанной зоне доминируют пластические механизмы деформирования, связанные с генерацией и движением дислокаций. Это приводит к реализации вязкого механизма распространения трещины, сопровождающегося образованием зоны пластичности у вершины трещины. Данная гипотеза основана на положении о том, что параметр жесткости напряженного состояния П является ключевым фактором, определяющим конкуренцию между хрупкими и вязкими механизмами разрушения в зоне предразрушения. Высокие значения П благоприятствуют локализации деформации и реализации механизмов хрупкого отрыва, в то время как низкие значения П способствуют активации дислокационных механизмов и развитию пластической деформации.

Для описания жесткости схемы напряженного состояния применяют различные показатели. Один из таких параметров, коэффициент жесткости П, является безразмерной величиной, характеризующей "трехосность" напряженного состояния. Его физическая интерпретация может быть дана через анализ условий пластичности. Согласно критерию Мизеса, пластическое течение начинается при достижении интенсивностью напряжений некоторого критического значения. Однако наличие гидростатической компоненты существенно влияет на процесс разрушения.

В работе [18] приводится коэффициент жесткости П, описываемый формулой (1):

П _ CT 1 +CT 2 +CT 3

Pi где <71, 02, о3 - компоненты главных напряжений, Oi - интенсивность напряженного состояния (2):

|g^^

ⁱ у 2

(О 2 —О 3 )²

(О 3 -О 1 ^{) 2}

В механике разрушения точное описание полей напряжений в окрестности вершины трещины позволяет представить поля напряжений в виде ряда, где каждый последующий член уточняет описание на больших расстояниях от вершины трещины. Для применения формулы (1) необходимо выразить компоненты тензора напряжений и, соответственно, главные напряжения через параметры этого разложения. Считается [19, 20], что первые два члена ряда в большинстве задач исследования поля напряжений у вершины трещины достаточны. Поле напряжений в окрестности вершины трещины с учетом двух членов ряда в случае трещины нормального отрыва описывается уравнениями (3).

OX =

О

K

cos-(1 — sin-sin3-) + Tx

2 \         2     2 У ^

K i

cos-(1 + sin-sin—) 2 V          2      2 у

,

Txy = -:=^ sin - cos - cos— ху V2nr    2    2     2

где TX - Т-напряжения, являющиеся первым несингулярным членом разложения [21].

Для анализа коэффициента жесткости П на линии продолжения трещины 0 = 0 уравнения (3) упрощаются:

Ox =

K= + Tx

Ътгг    ^X

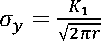
^ху   0

Компонента o_z в зависимости от типа напряженного состояния (для плоского напряженного состояния, ПНС; и для плоского деформированного состояния, ПДС) будет иметь вид:

( o_z = 0 для ПНС

Oz = ^(ох + Оу) = м (^ + Tx) для ПДС ■

Поскольку, согласно вышеописанной гипотезе, коэффициент жесткости необходимо рассчитать на границе зоны пластичности, перепишем уравнения (4) в терминах главных напряжений на расстоянии г_р. На линии продолжения трещины (0 = 0) касательные напряжения равны нулю, следовательно, компоненты о_х , О у , o_z совпадают с главными напряжениями О 1 , о₂, О₃.

В случае положительных Т-напряжений получаем:

г

О 1

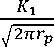
+ Тх

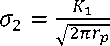
/з = М (

2K 1

12пгр

+ Тх)

для ПДС, и о3 = 0 для ПНС

Если уравнения (6) подставить в (1) и упростить, используя следующую замену:

T T\2F7 : ,

получим следующие выражения для коэффициента жесткости:

Для случая ПНС:

_     2К 1 +Т *

^К 1² +К 1 Т * +Т *²

.

Для случая ПДС:

П =

1+м _______

, 3Ki(Ki+F) ^.

1  (2К1+Т*)2

Результаты расчетов по уравнениям (8) и (9) представлены в виде трехмерных поверхностей (рис. 1) и в виде полей коэффициента жесткости на контурных диаграммах (рис. 2). На рисунках показаны случаи плоского напряженного состояния (слева), описываемые уравнением (8), и плоской деформации (справа), описываемые уравнением (9).

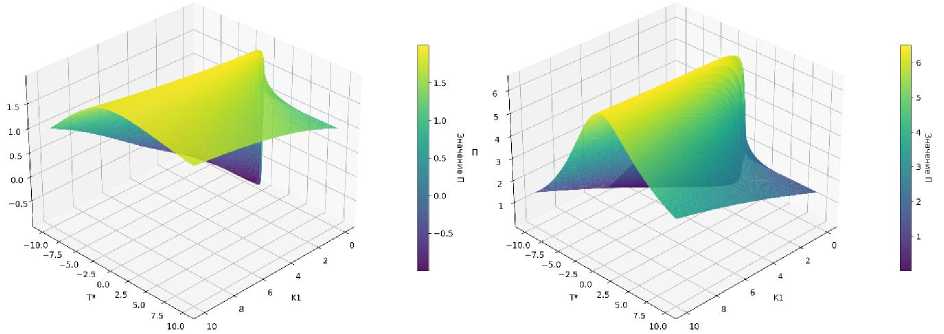
Рис. 1. Трехмерное представление зависимости коэффициента жесткости Π от параметров напряженного состояния: слева – расчет для ПНС; справа – для ПДС

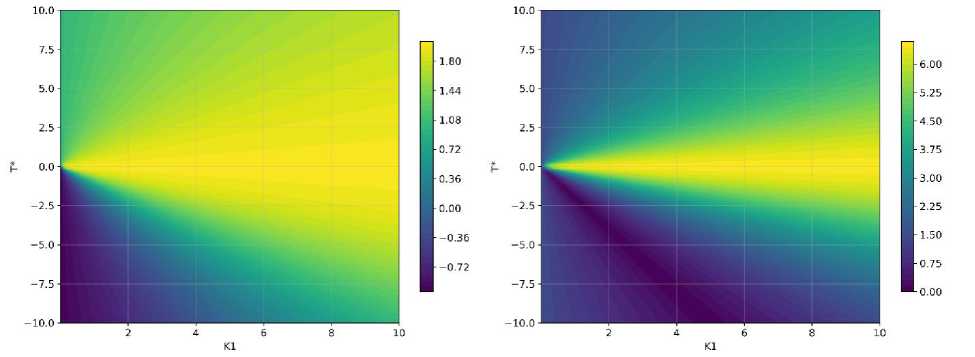
Рис. 2. Поле коэффициента жесткости напряженного состояния: слева – для ПНС, справа – для ПДС

Из рисунков 1 и 2 видно, что напряженное состояние с максимальными значениями коэффициента жесткости соответствуют линии Т * = 0, особенно для случая плоской деформации. Это может означать, что малый радиус зоны пластичности с одновременно около-нулевыми значениями Т-напряжений, действующих в условиях плоской деформации, может существенно повысить склонность материала хрупкому разрушению. И, напротив, больший радиус зоны пластичности и большие значения Т-напряжений, особенно в сторону отрицательных значений, обуславливают " мягкое " напряженное состояние, при котором наиболее вероятно вязкое разрушение.

В уравнениях (5) и (6) одним из переменных является радиус зоны пластичности тр. Размеры пластической зоны на линии продолжения трещины (0 = 0) по условиям текучести Мизеса представлены в следующем виде [22]:

Для плоского напряженного состояния:

К 1 2710 ? .

Г =

Для случая плоской деформации:

Гр =

К 1 18па 2 .

Подставив выражения (10) и (11) в уравнения (6), (7), и в конечном итоге в (1), получим возможность численного расчета коэффициента жесткости П на конкретном примере. В качестве примера выбран образец на трехточечный изгиб. Реализация расчетов П выполнена с помощью методов компьютерного программирования.

Коэффициенты интенсивности напряжений K₁ и T-напряжения рассчитывались на основе табличных данных для схемы трехточечного изгиба, представленной на рис. 3, полученных методом применения функции Грина [23].

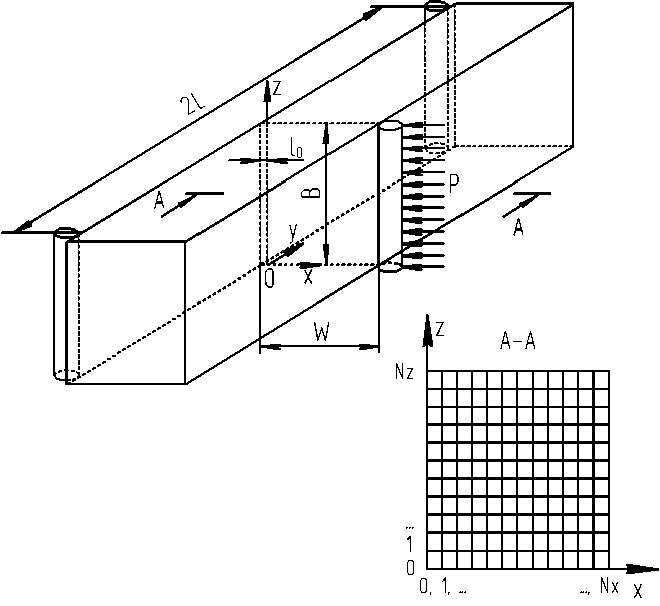
Рис. 3. Вид, размеры и схема разбиения сечения образца на расчетные элементы

Как видно из рис. 3, начало координат находится на вершине начальной трещины длиной 1₀. Ширина образца по оси z - B, расстояние между упорами - 2L, глубина по оси x – W. Сечение образца по плоскости трещины A-A показано справа. Выполнено разбиение сечения на расчетную сетку с N x элементами по оси x и N z элементами по оси z. Алгоритм компьютерного расчета коэффициента жесткости напряженного состояния представлен на рис. 4.

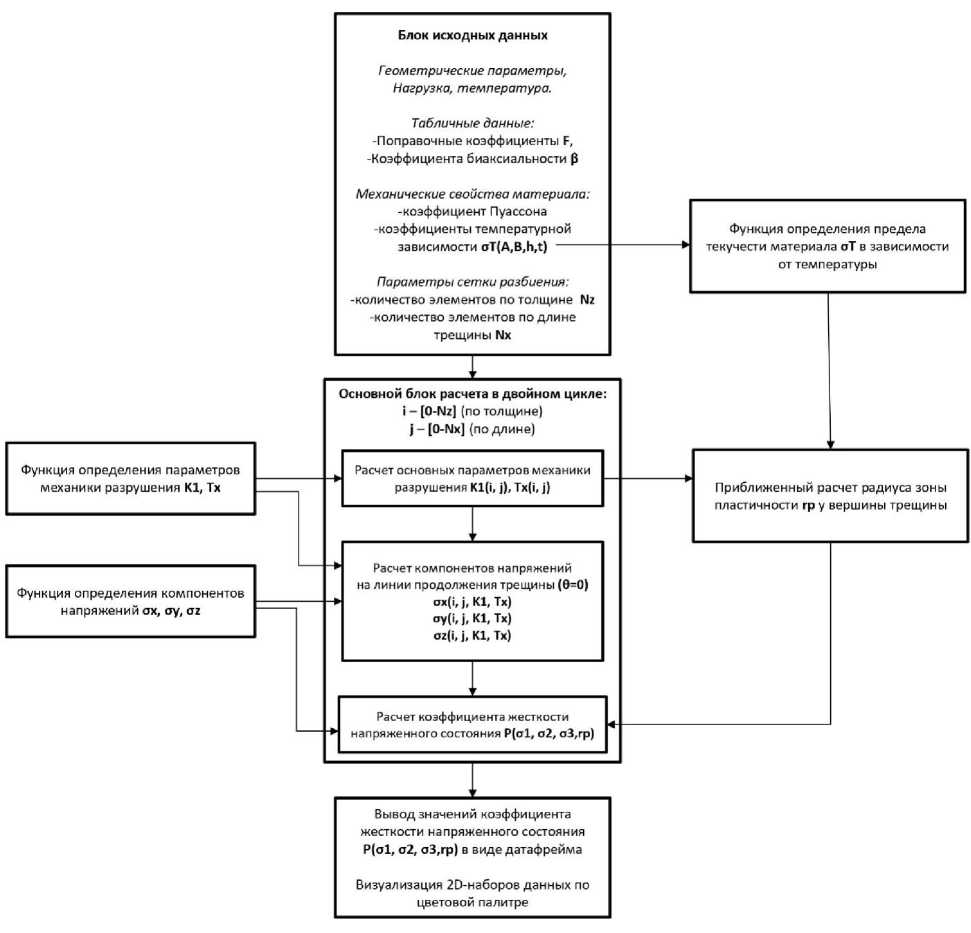
Рис. 4. Алгоритм расчета коэффициента жесткости напряженного состояния

Основной расчет проводится в двойном цикле по i (счетчик, привязанный к координатам по оси z) и j (счетчик, привязанный к координатам по оси x – длине трещины. Таким образом, последовательно рассчитывается значение П по всему сечению модели образца. На каждый элемент (i, j) в расчет берутся соответствующие значения длины трещины, коэффициента интенсивности напряжений, Т-напряжений, радиуса зоны пластичности, которые, в свою очередь, автоматически рассчитываются в виде выходных параметров соответствующих функций программы. Температура, как один из входных параметров в данном расчете, является параметром предела текучести материала, который увеличивается при понижении температуры, и должна быть задана как функция программы в том или ином виде. Далее предел текучести напрямую влияет на размер зоны пластичности и, например, чем меньше радиус зоны пластичности, тем больше станут значения коэффициента жесткости напряженного состояния.

Обсуждение результатов

На рисунках 5 и 6 представлены результаты расчетов значений коэффициента жесткости напряженного состояния моделей образцов с толщинами 10 мм и 3 мм, соответственно [24]. На правой части показаны изломы образцов, испытанных на ударную вязкость, с долей вязкой составляющей 20% и 40%.

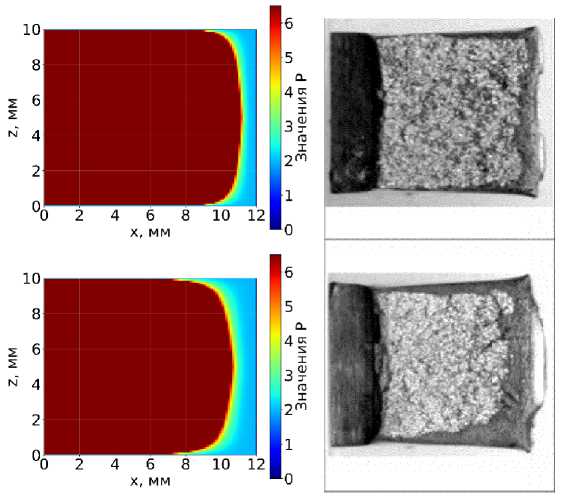
Рис. 5. Результаты расчетов коэффициента жесткости напряженного состояния для модели образца, толщиной 10мм. Верхние – 20% вязкой составляющей излома, нижние – 40% вязкой составляющей излома

Следует отметить визуальное соответствие между результатами расчетного моделирования и экспериментальных данных. В частности, наблюдается сходство между прогнозируемым распределением вязких и хрупких зон в расчетной модели и фактической морфологией излома: области, характеризующиеся вязким разрушением в периферийных зонах и зоне окончательного долома, идентифицированные в ходе моделирования, согласуются с экспериментально наблюдаемыми участками вязкого разрушения.

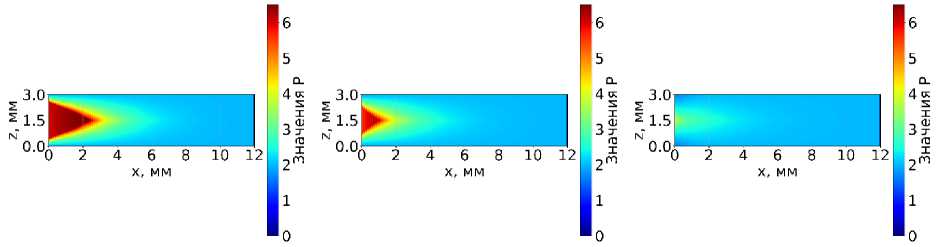
Рис. 6. Результаты расчетов коэффициента жесткости напряженного состояния для образца толщиной 3 мм

Для образца толщиной 3 мм при идентичных условиях нагружения моделирование проводилось для материала с тремя разными значениями предела текучести: базовым значением σ_T, а также со сниженными значениями 0.75σ_T и 0.5σ_T (рис. 6). Во всех случаях формируется " мягкое " напряженное состояние. Результаты соответствуют известной закономерности, согласно которой для образцов малой толщины характерно преобладание механизмов вязкого разрушения, что обусловлено реализацией условий плоского напряженного состояния.

В контексте оценки ударной вязкости следует подчеркнуть определяющую роль пластической составляющей в общем балансе энергии разрушения. Учитывая, что процесс распространения трещины сопровождается непрерывной эволюцией параметров механики разрушения и характеристик пластических зон, а конечный результат традиционно характеризуется единственным параметром (KCU или KCV), представляется методологически обоснованным внедрение более совершенных подходов к оценке сопротивления хрупкому разрушению. Перспективным направлением представляется разработка методик, основанных на анализе коэффициента жесткости напряженного состояния, который обладает более высокой чувствительностью к особенностям кинетики разрушения и позволяет осуществлять дифференцированную оценку сопротивления материала распространению трещины на различных стадиях процесса разрушения.

Традиционные материаловедческие исследования, основанные на фрактографическом анализе изломов, как правило, не учитывают расчетные методы механики разрушения. Настоящее исследование предлагает междисциплинарный подход, интегрирующий количественные параметры механики разрушения, в частности коэффициент жесткости напряженного состояния, с качественным анализом микроструктуры. Разработанный критерий вязко-хрупкого перехода восполняет существующий методический разрыв и создает основу для комплексного анализа процессов разрушения, объединяющего материаловедческие и механико-математические методы исследования.

Заключение

Разработан алгоритм расчета распределения коэффициента жесткости вдоль фронта трещины.

Предложен способ прогнозирования характера разрушения материала, основанный на анализе распределения коэффициента жесткости напряженного состояния P вдоль фронта трещины.

Показано, что малый радиус зоны пластичности с одновременно около-нулевыми значениями Т-напряжений, действующих в условиях плоской деформации, может существенно повысить склонность материала хрупкому разрушению; и, напротив, больший радиус зоны пластичности и большие значения Т-напряжений обуславливают " мягкое " напряженное состояние, при котором наиболее вероятно вязкое разрушение.