Модельное исследование перспектив развития научной отрасли Российской Федерации

Развитие научной отрасли любого государства является важной задачей, поскольку успехи этой отрасли могут явно отражаться во всех других сферах общества. «Следует сосредоточить повышенное внимание на развитии фундаментальной науки, нацелить её на получение принципиально новых знаний, поиск ответов на так называемые большие вызовы завтрашнего дня» – отмечено на заседании Совета по науке и образованию при Президенте РФ от 23.11.2016 [7].

Целью данной работы является построение прогнозной модели общего состояния научной отрасли Российской Федерации для поддержки принятия решений и прогноза на ближайшее будущее.

Существуют различные виды моделей: линейные многофакторные (ЛММ) [1, 6], регрессионно-дифференциальные (РДМ) [9, 12], модели пространства состояний (МПрС) [4] и другие. Каждые из них имеют свои особенности и недостатки. Так, например, ЛММ являются простыми и хорошо объясняющими, а РДМ имеют способность к прогнозированию, что и требуется для достижения цели данной работы.

Для сбора данных об исследуемом объекте в этой работе использовался общедоступный сервис Федеральной службы государственной статистики [17].

В данной работе для оценки качества исследуемого объекта были выбраны его следующие реакции, которые в конечном итоге составили общий критерий оценки объекта ( y ₀) : количество выдаваемых патентов ( y ₁) , численность исследователей, имеющих ученую степень ( y ₂), и используемые передовые производственные технологии в целом ( y ₃ ) .

В качестве внешних воздействий среды на исследуемый объект были выбраны следующие показатели: количество поданных заявок на выдачу патентов ( x ₁) , число организаций, выполняющих научные исследования и разработки ( x ₂) , численность персонала, занятого научными исследованиями и разработками ( x ₃) , внутренние затраты на исследования и разработки ( x ₄) , разработанные передовые производственные технологии ( x ₅) , выпуск из аспирантуры с защитой диссертации ( x ₆) , число организаций, ведущих подготовку аспирантов ( x ₇) , выпуск из докторантуры ( x ₈) , число организаций, ведущих подготовку докторантов ( x ₉) .

Выбор реакций объекта как общий критерий оценки качества исследуемого объекта вполне пригоден для исследования, потому как отражает результат работы вузов, деятельности исследователей и пригодность использования полученных результатов в производстве.

Выбор факторов также не противоречит здравому смыслу, ибо количество организаций, подготавливающих высокообразованные кадры, результат их работы и их финансовое обеспечение напрямую влияют на объект исследования – качество научной сферы страны.

Годовые ряды факторов и реакций представлены в табл. 1.

Таблица 1

Годовые ряды данных о факторах и частных критериях

Критерий	Год
	2007	2008	2009	2010	2011	2012	2013	2014	2015	2016	2017
и фак-						№ года
торы	1	2	3	4	5	6	7	8	9	10	11
y 1	23,028	28,808	34,824	30,322	29,999	32,88	31,638	33,95	34,706	33,536	34,254
y 2	103725	101049	101275	105114	109493	109330	108248	109598	111533	108388	103327
y 3	180,324	184,374	201,586	203,33	191,65	191,372	193,83	204,546	218,018	232,388	240,054
x 1	39,439	41,849	38,564	42,5	41,414	44,211	44,914	40,308	45,517	41,587	36,454
x 2	3957	3666	3536	3492	3682	3566	3605	3604	4175	4032	3944
x 3	801135	761252	742433	736540	735273	726318	727029	732274	738857	722291	707887
x 4	371080,3	431073,2	485834,3	523377,2	610426,7	699869,8	749797,63	847527	914669,1	943815,2	1019152,4
x 5	780	787	789	864	1,138	1,323	1,429	1,409	1,398	1,534	1,402
x 6	10970	8831	10770	9611	9635	9195	8979	5189	4651	3730	2320
x 7	1490	1529	1547	1568	1570	1575	1557	1519	1446	1359	1284
x 8	429	297	435	336	382	394	323	231	181	151	65
x9	579	593	598	602	608	597	585	478	437	385	223

Первым делом необходимо исключить влияние размерности используемых данных. Для этого нужно найти минимальное и максимальное значения по всем отсчетам и рассчитать нормированные значения частных критериев и факторов. Например, для критериев формула расчета будет выглядеть следующим образом:

y * ( t k ) =

y i ⁽ t k ) - min y i ⁽ t k ) t

max У1(tk) - min yi(tk), tt где tk ={ti,t2,...,tK}, k= 1, K - номер отсчета. Аналогично и для факторов.

Далее следует составить общий критерий (y0) на основе частных, выбрав наиболее подходящую комбинацию рангов для каждого из частных критериев. Подходящая комбинация должна быть такой, чтобы она менялась между моментами измерений как можно меньше, так как рассматривается большая социально-экономическая система, которая не может меняться резко. Формула получения общего критерия:

y o( tk) = 2 ^i (tk), (2) t где ai – вес i-го критерия. Обычно путем экспертных заключений или на основании дополнительной информации определяются ранги значимости частных критериев Ri, при этом меньшие значения рангов соответствуют большей значимости критериев [13, 15, 19].

a =—, iRi где Ri – ранг i-го критерия. Для поиска оптимальной комбинации рангов необходимо, чтобы критерий между моментами измерений менялся как можно меньше:

K - 1

^ min.

R : 2 к ( t k + 1 ) - Y ( t k )

K = 1

Результат поиска значений рангов: R 1 = 3, R ₂ = 2, R 3 = 1. Результирующий график общего критерия можно увидеть на рис. 1. Так как чем меньше значение ранга, тем значимее критерий, можно сделать вывод, что кол ичество используемых передовых производ ственных технологий наиболее сильно влияет на исс ледуемый объект, в то время как количество выдаваемых патентов имеет наименьший э ффект. Эт о, наверное, можно объяснить тем, что дале ко не все патенты н а чинают сразу же активно прим еняться и, быть может, это имеет долгосрочн ый эффект.

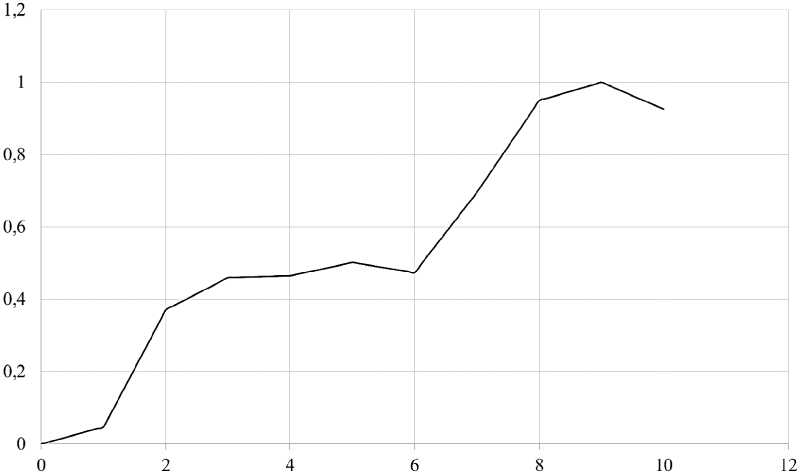
Рис. 1. График результирующего критерия

Исследуем возможность применения ЛММ в данном случае. Попробуем построить линей ную многофакторную модель (ЛММ) вида

У о ( x ( t ) ) = ^a 0 + Z ^a i x i ( t ) ,                                                                          ⁽⁵⁾

i где ai – коэффициенты влияния i-го фактора.

Обычно перед построением ЛММ проводят анализ выбранных факторов на их взаимную корреляцию, поскольку факторы с высокой взаимной корреляцией могут не позволить определить их изолированное влияние на результат и их следует исключать [10, 11, 16]. Рассчитаем взаимную корреляцию факторов. В табл. 2 видно, что разрабатываемые передовые производственные технологии напрямую зависят от финансирования. А, например, число организаций, ведущих подготовку докторантов и выпуск докторантов, зависит от выпуска аспирантуры, что логич- но. В то же время выпуск из аспирантуры по какой-то причине обратно пропорционален внутренним затратам, т. е. коэффициент корреляции меньше нуля.

Исключим из модели факторы: выпуск из аспирантуры с защитой диссертации (x6) и число организаций, ведущих подготовку аспирантов (x7) , так как их парная корреляция слишком высока.

Таблица 2

Парная корреляция

	x 1	x 2	x 3	x 4	x 5	x 6	x 7	x 8	x 9
x 1	1	–0,022	– 0,066	0,051	0,271	0,147	0,453	0,142	0,403
x 2	–0,022	1	0,094	0,473	0,364	–0,599	–0,749	–0,584	–0,643
x 3	–0,066	0,094	1	–0,770	–0,714	0,595	0,303	0,566	0,495
x 4	0,051	0,473	– 0,770	1	0,929	–0,913	–0,671	–0,851	–0,819
x 5	0,271	0,364	– 0,714	0,929	1	–0,750	–0,452	–0,665	–0,600
x 6	0,147	–0,599	0,595	–0,913	–0,750	1	0,835	0,975	0,931
x 7	0,453	–0,749	0,303	–0,671	–0,452	0,835	1	0,843	0,953
x 8	0,142	–0,584	0,566	–0,851	–0,665	0,975	0,843	1	0,920
x 9	0,403	–0,643	0,495	–0,819	–0,600	0,931	0,953	0,920	1

Погрешность прогнозирования рассчитывается по формуле K

S прогн = E ( У 0 ( t k ) - У ( t k ) ) ^ min,                                                           ⁽⁶⁾

k = 1

где y ₀ ( t_k ) - известное значение ; y ( t_k ) - расчетное значение.

Задачу минимизации можно решить методами покоординатного или гради ентного спуска [14]. На рис. 2 изображен график пост роенной модели с постпрогнозом на один го д. По графику мо жно увиде ть, что постпрогноз у Л ММ очень плохой, поскольку значение постп рогноза больше исходных данных на целых 50 %. П оэтому она не может применяться для прогно зирования объекта.

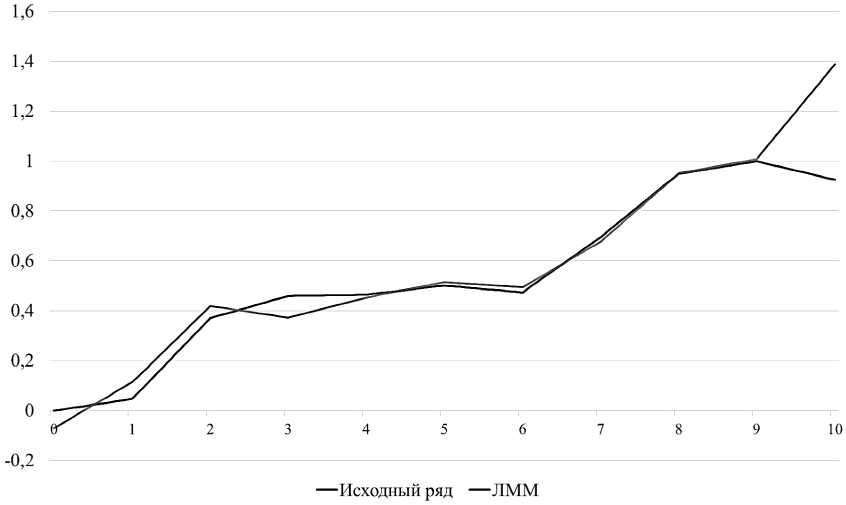
Рис. 2. ЛММ

Теперь попробуем построить с помощью данного ПС РДМ вида m y'(t ) = a + b • y (t ) + 2 Ci- Xi (t),                                                                       (7)

i = 1

где a – константа, описывающая влияние одной n-й производной реакции при построении трен- да; b – коэффициент «обратной связи», описывающий влияние значения реакции на ее же n-ю производную; ci – коэффициенты влияния факторов. Также РДМ дополняется начальным усло- dy (0)    , вием —= y0 .

dt ⁰

Неизвестными в данном случае являются y’ , a , b , c i . Их поиск производится минимиза цией квадратичного отклонения расчетного значения от известных в отсчетах значений критерия:

K—12

• 5    = £( y (tk)- у о (tk)),

к = 0

где y ₀ ( t_k ) - известное значение ; y ( t_k ) - расчетное значение.

Задача минимизации сводится к

• {y ', a, b, Ci}: 5 {y', a, b, ct }^ min.

Следующим шагом подбер ем комбинацию интерполяций для каждого ф актора из возможных вариантов: левая – значение ф актора действует с начала до конца промежу тка времени; правая – значение в статистике приведено на к онец года; линейная – значение, которое изменяется до конца года. Также можно выкл ючить фактор, если при этом определится, ч то исключение факт о ра несущественно повлияет на качество аппроксимации.

В результате мы имеем следующую РДМ (рис. 3), которая наиболее точно аппроксимирует исходные данные.

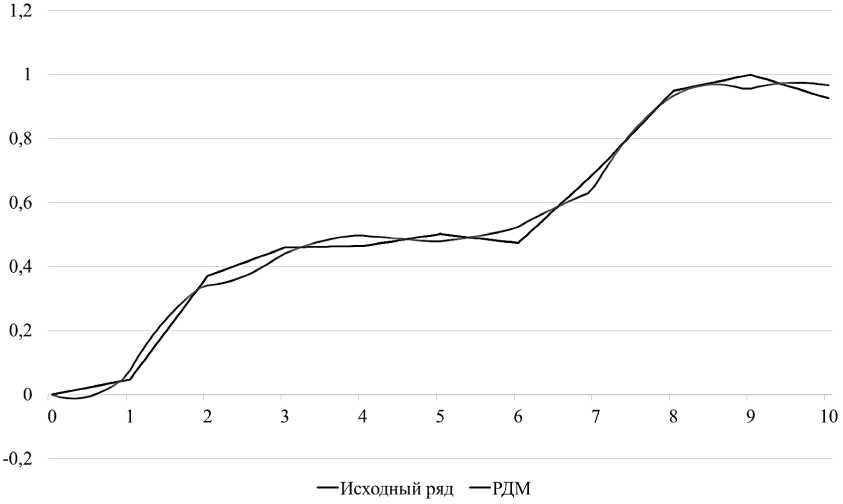
Рис. 3. РДМ

При этом мы имеем следующе коэффициенты влияния факторов (табл. 3).

Таблица 3

Коэффициенты влияния факторов

c 1	c 2	c 3	c 4	c 5	c 6	c 7	c 8	c 9
0	0	0	0,7097	–0,5673	–0,6069	0,8901	–0,5372	0,2253

Видно, что количество поданных заявок на выдачу патентов (x1) , число организаций, занимающихся научными исследованиями и разработками (x2) и численность персонала, занятого научными исследованиями и разработками (x3) , оказались выключенными факторами, и они никак не влияют на критерий построенной модели. Число организаций, ведущих подготовку аспирантов (x7) и внутренние затраты на исследования и разработки (x4) , имеют наибольший положительный эффект на научную отрасль Российской Федерации. А вот наибольший отрицательный эффект оказывает выпуск из аспирантуры (x6) , что немного странно, но можно попробовать объяснить это тем, что увеличение количества разработанных ими технологий замедляет скорость внедрения их в производстве.

Поскольку целью данной р аботы является прогнозирование исследуемо го объекта, то ра с смотрим прогнозные свойства получен ной модели. Применим широко известный метод постпрогноза [2], основанный на расчёта х реакций модели на известные данные в теч ени е последних лет. Определим допустимый горизон т прогнозирования данной модели. Для этого следует уменьшать количество известных л ет в расчете модели ( рис. 4), чтобы определить момент, когда погреш ность прогноза станет значительной [3].

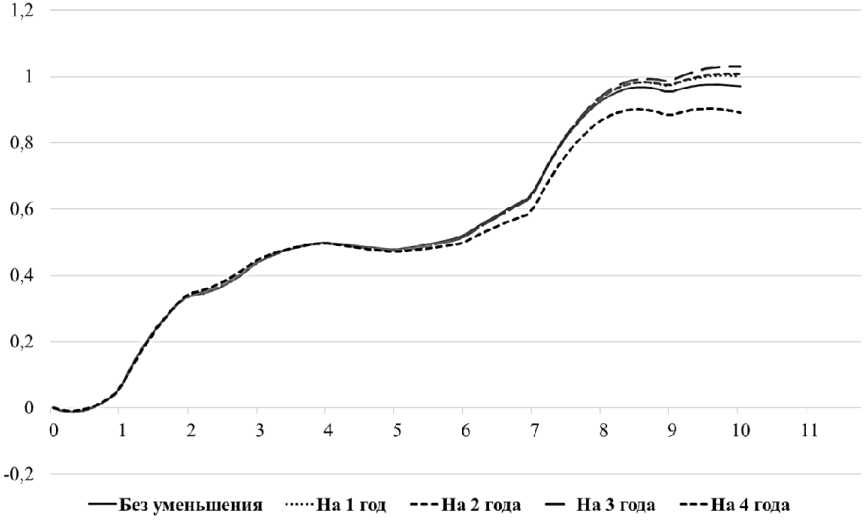
Рис. 4. Уменьшение известных лет

Уменьшение известных лет на 4 года уже значительно изменило поведени е модели.

Исходя из полученных резул ьтатов, можно предположить, что допустим ый горизонт прогн о зирования данной модели составляет 3 года.

Прежде чем прогнозироват ь реакцию объекта, надо спрогнозировать значения факторов. Примем допущение, что предоставленные сами себе факторы будут изменяться так же, как они менялись за несколько последн их лет. Нужно определить регрессионное ур авнение их повед е ния в заданной ретроспективе и рассчитать их значения в соответствии с на йденным уравнен ием [1, 5, 8, 18, 20].

Выделим три следующих воз можных уравнения регрессии факторов:

• 1.    Фактор изменяется квадратично, то есть x ( t ) « a + bt + ct 2 .

• 2.    Фактор изменяется линейно, т. е. x ( t ) « a + bt .

• 3.    Для фактора не подходит ни квадратичный, ни линейный закон. Напр имер, значения фа к тора хаотично меняются вокруг какого -то среднего значения x ( t ) = x ± A x . В этом случае будем считать, что предоставленный са м себе фактор будет оставаться на уровне о дного из значений в пределах x ± A x . В том числе можно ис пользовать последнее значение годового ряда.

Для определения вида по дходящей регрессии фактора вычислим коэ ффициенты линейной корреляции R ² , характеризующие близость исходных данных к полученным регрессией. Принято, что если R ² >  0,95 , то выбранн ый вид регрессионной зависимости удовлетв орительно описывает поведение фактора в пределах ретроспективы. Причем, поскольку линейн ая регрессия является частным случаем квадратичной , алгоритм выбора вида регрессии следующи й:

• 1.    Если для линейной ре грессии R ² >  0,95 , то вид регрессии - линейный.

• 2.    Иначе если для квадратичной регрессии R ² >  0,95 , а для линейной R ² <  0,95 , то вид регрессии – квадратичный.

• 3.    Иначе использовать последнее значение годового ря да.

Теперь, после получения п рогноза значений факторов, попробуем спрог нозировать объект на три года вперед ( рис. 5).

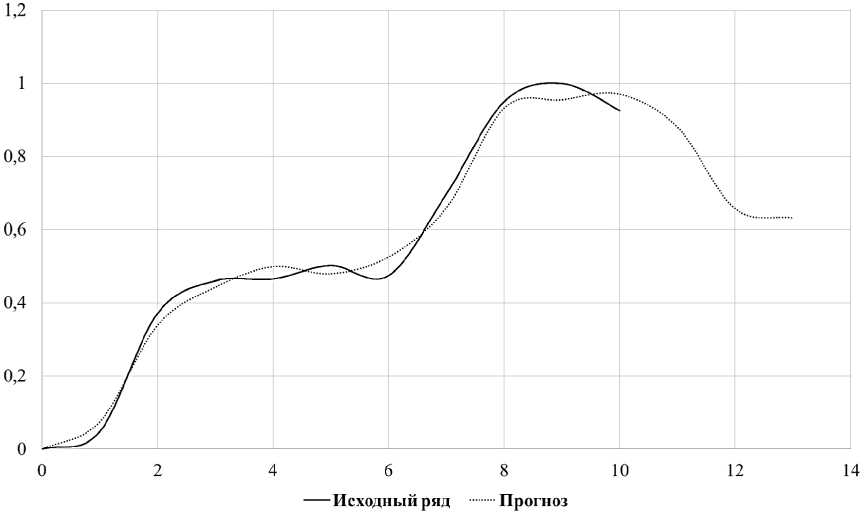
Рис. 5. Прогноз на 3 года

По данному прогнозу мож но предположить, что если оставить «все ка к есть», то в ближа йшее время в течение 3 лет пока затели научной отрасли Российской Федерац ии упадут на 31,7 %.

Попробуем осуществить н ебольшое воздействие на некоторые факторы , которые могут быть управляемыми. Например, вну тренние затраты на исследования и разработ ки ( x ₄) и число орга низаций, ведущих подготовку аспирантов ( x ₇) (табл. 4).

Прогноз на три года при изменении управляемых факторов

Таблица 4

Изменение фактора	Номер года
	1	2	3
x 4 – 10 %	0,8739	0,6404	0,6012
x 4 + 10 %	0,8866	0,675	0,6628
0 %	0,88	0,6572	0,632
x 7 – 10 %	0,89	0,6922	0,7016
x 7 + 10 %	0,8701	0,6223	0,5623

В результате видно (рис. 6), что увеличение внутренних затрат на разработки и исследования на 10 % приведет к уменьшению падения уровня научной отрасли РФ на 3,32 %, т. е. общее па- дение научной отрасли уже будет составлять 28,2 %. Если же данный фактор уменьшить на 10 %, то скорость падения объекта увеличится на 3,32 %. Число организаций, ведущих подготовку аспирантов, обратным путём влияет на объект, так как уменьшение данного показателя на 10 % ведет к сокращению падения научной отрасли РФ на 7,5 %, и тогда общее падение будет составлять 24 %. Изменение показателя в другую сторону приведет уже к падению науки на 39,2 %.

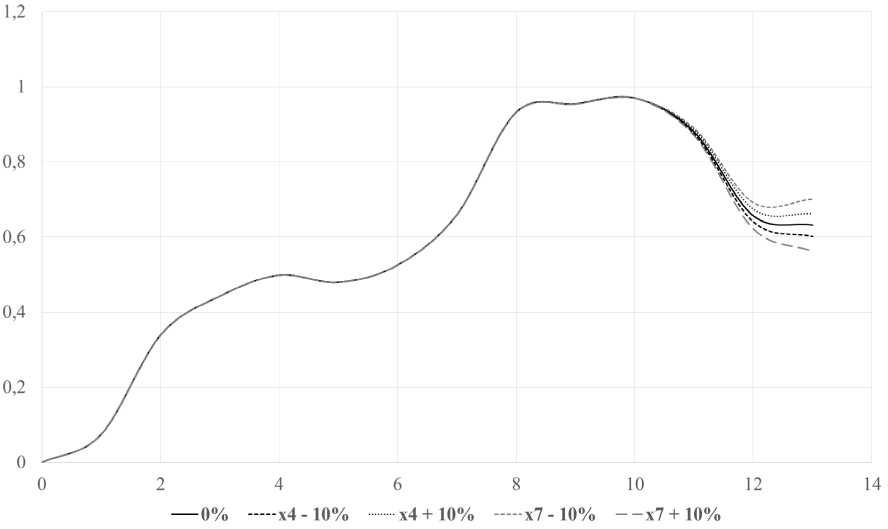
Рис. 6. Изменение факторов x ₄ и x ₇

Примем тот факт, что выпуск из аспирантуры с защитой диссертации ( x ₆) и выпуск из докторантуры ( x ₈) являются неупра вляемыми факторами и на них невозможно никак повлиять. Так как оба эти фактора имеют отри цательный коэффициент влияния, то рассмот рим ситуацию с о д новременным ростом данных показателей на 5 %, что отрицательно скажется на исследуемом объекте (табл. 5).

Таблица 5

Прогноз на три года с учетом неуправляемых факторов и изменения управляемых факторов

Изменение фактора	Номер года
	1	2	3
0 %	0,88	0,6572	0,632
x 6 + 5 %, x 8 + 5 %	0,8691	0,6035	0,5376
x 6 + 5 %, x 8 + 5 %, x 4 + 10 %, x 7 – 10 %	0,8757	0,6562	0,638

В этом случае научную отрасль ожидает падение уже на 41,9 %, что на 10,2 % хуже, чем до изменения неуправляемых факторов. Поэтому, чтобы лицу, прини мающему решение (ЛПР), исправить данную ситуацию, необходимо воздействовать каким-то образом на управляемые факторы. Как показало исследование, решить данную проблему можно с помощью увеличения внутренних затрат ( x 4 ) на 10 % и уменьшения числа организаций, ведущих подготовку аспирантов ( x 7 ), на 10 %. Это исправит ситуацию на 10,8 %, и тогда падение научной отрасли будет даже ниже на 0,6 % относительно положения до изменения неуправляемых факторов (рис. 7).

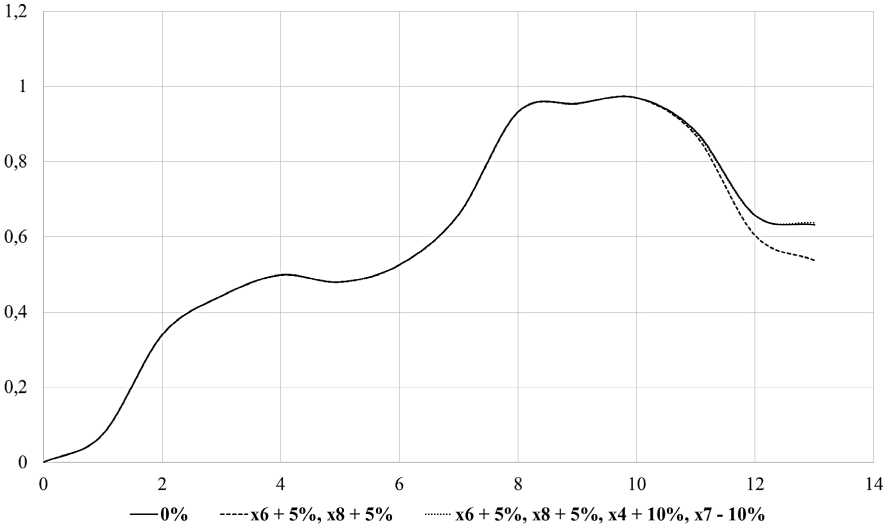
Рис. 7. Изменение неуправляемых факторов

В результате данной работы была построена прогнозная математическая модель общего со стояния научной отрасли Росс ийской Федерации. Как показало исследова ние, наиболее важное значение для научной отрасли России в рамках данной модели имеют внут ренние затраты на и сследования и разработки, а так же число организаций, ведущих подготовку аспирантов. Обратное влияние оказывают такие факт оры, как разработанные передовые производ ственные технологии, выпуск из аспирантуры и док торантуры. Из полученных результатов про гноза можно сделать вывод, что в ближайшее врем я научную отрасль страны ожидает отрицат ельная динамика и за три года она упадет на 31,7 %. Если внутренние затраты на исследования и разработки увеличить на 10 %, то отрицательная динамика станет на 3,3 % лучше. А если уменьшить число организа ций, ведущих подготовку аспирантов, на 10 %, то отрицательная динамика станет лучше на 7,5 %. Влияние неуправляемых факторов может оказать на объект еще бол ее усугубляющие п о следствия. Например, рост вы пускников аспирантуры и докторантуры на 5 % приведет к падению научной отрасли на 41,9 %. Чтобы исправить данную ситуацию, ЛПР может повлиять на управляемые факторы, что может привести к улучшению динамики на 10,8 %.