Модельное исследование совместной работы участков производства губчатого титана

Основным способом производства титана в России и за рубежом является восстановление тетрахлорида титана магнием по способу Кроля. Таким образом производится титановая губка на предприятиях бывшего СССР (в том числе в Казахстане и на Украине), в Китае, США и Японии [1]. Современные усилия по разработке альтернативных технологий, основанных в основном на восстановлении диоксида титана, пока находятся на стадии лабораторных и опытно-внедренческих исследований [2, 3]. Вопросы производства губчатого титана близки к стратегической и оборонной тематике, поэтому в научных статьях в журналах (кроме РФ) освещены слабо. Советская технология производства описана в классической монографии [4] и является сложной, энергозатратной и многопередельной. Крупнейшим производителем титановой губки в мире (порядка 40 тыс. т в год) является корпорация «ВСМПО-Ависма», собственно производство губки осуществляется в филиале «Ависма» в г. Березники Пермского края.

На этом предприятии существует проблема рассогласования планов работы двух основных производственных участков – восстановления титана (ОПУ-2, цех 35) и электролиза магния (ОПУ-3, цех 31). Из-за стохастических отклонений, вызванных независимыми друг от друга планами и стараниями персонала выполнить их любой ценой, возникают сбои в обеспечении ОПУ-2 донными ковшами. При этом для выполнения плана персонал ОПУ-2 вынужден сливать расплав хлорида магния в короба с последующей длительной и дорогой подготовкой его к электролизу (рис. 1).

Авторами в предыдущих работах предложено решать данную проблему путем управления по модели совместной работы участков или создания системы поддержки принятия решений (СППР)

диспетчера по аналогии с [5]. В мировых источниках использование имитационных моделей в управлении производством освещены достаточно широко (например, [6]) и позволяет получать положительные эффекты на всех стадиях жизненного цикла [7]. Подобные попытки для титанового производства также производились [8, 9]. В первой из работ на языке Фортран написана имитационная модель совместной работы участков восстановления и сепарации губчатого титана. И модель, и ее реализация выполнены в духе, свойственном тем годам (монография опубликована в 1991 г.), в постановочной части есть неясности в смысле принятых допущений об элементарных ячейках системы массового обслуживания (СМО), не приведены сведения о погрешности модели, полученные путем сравнения результатов расчетов с данными действующего производства. Участок электролиза магния в монографии не рассмотрен. Во второй работе очень скупо описана сама модель вспомогательных подразделений, даже не приведена информации о ее погрешности. Вкупе с особенностями системы моделирования AnyLogic (включая высокую лицензионную стоимость) это привело авторов к идее разработки собственной библиотеки моделирования и реализации в ней модели совместной работы двух ОПУ [10]. Оснащение модели произведено на основе данных, полученных непосредственным измерением таймингов процессов на участках и между ними, выполненных в 2016 году [11]. Показано, что модель имеет погрешность порядка 7–8 % и может использоваться в составе СППР, то есть адекватно отражает процессы, происходящие на участках.

Производится 1 раз из электролизера за 1 час

Монтаж

Ожидание

Демонтаж

Цикл печи (46 шт)

Процесс \ восстановления

Ожидание слив;

2.5^3 мин

Транспортировка в ц. 35

Цикл электролизера (64 шт)

2.5^3.5 мин

Слив хлорида \ магния

Цикл ковша

Слив дляI электролизера

1^1.5 мин

Транспортировка в ц. 31

Производится 7 раз за смену ---- через 1 час 10 минут.            ' '

(7 шт, 4 тн)

Ожидание слива в электролизер^

Норматив 400-500 кг, бывают

отклонения 300-700 кг.

Общая масса слива 14700 кг

Рис. 1. Системный анализ совместной работы ОПУ-2 и ОПУ-3

Целью настоящей статьи является применение разработанной программной модели для поиска сочетаний условий, при которых сливы в короба исключаются. Из всех 46 факторов модели, большая часть которых упомянута на рис. 1, в качестве управляемых были выбраны следующие:

• •    количество донных ковшей ( x 1 ) при принятом допущении, что каждый ковш бесперебойно комплектуется электрокарой;

• •    количество вакуумных ковшей ( x 2 );

• •    максимальное количество одновременно монтируемых аппаратов восстановления ( x 3 );

• •    остаток свободной вместимости, при достижении которого донный ковш отправляется на электролиз, не дожидаясь его полного заполнения, кг ( x 4 );

• •    максимальное и минимальное время транспортировки донного ковша в ОПУ-3, мин ( x 5 );

• •    максимальное и минимальное время отстоя вакуумного ковша, мин ( x 6 );

• •    максимальное и минимальное время монтажа аппарата восстановления, мин ( x 7 );

• •    максимальное и минимальное время слива хлорида магния в донный ковш, мин ( x 8 ).

Выбор факторов обусловлен их важностью для производства и управляемостью, в отличие от многих других. Например, объем донного ковша, вместимость вакуумного ковша, вместимость донного ковша, количество печей восстановления, количество электролизеров, количество магния, заливаемого из миксера в реторту, нельзя легко изменять. Это привело бы к необходимости заменить оборудование, чтобы увеличить или уменьшить его объем, вместимость, а также увеличить или уменьшить количество оборудования, площади цехов и т. д.

В качестве реакций модели были выбраны следующие:

• •    производительность участка восстановления, т (количество сливов хлорида магния в донные ковши и в короба) ( y 1 );

• •    в том числе количество сливов в короба, т ( y ₂);

• •    среднее время ожидания в очереди на слив из донного ковша в ОПУ-3, мин ( y ₃).

С каждым выбранным фактором были проведены имитационные эксперименты. При этом сначала изменяли только один фактор, другие оставляли неизменными. Начальные значения факторов были установлены такими, какие они есть на действующем производстве: x 1 = 7, x 2 = 3, x 3 = 2, x 4 = 200 кг, x 5 = 4,5…5 мин, x 6 = 20…22 мин, x 7 = 70…80 мин, x 8 = 2,5…3,5 мин, все распределения равномерные.

Так как модель совместной работы участков стохастическая, каждый прогон модели выдает результат, отличающийся от всех других. Поэтому итоговые результаты получали методом установления, повторяя запуск модели с одними и теми же исходными данными до тех пор, пока математическое ожидание результата не перестанет изменяться в пределах 5 % (в соответствии с рекомендациями [12]).

Наиболее влияющим на количество (тоннаж) сливов в короба y ₂ оказалось количество донных ковшей x 1 . Из рис. 2 видно, что эта зависимость имеет выраженный нелинейный характер, то есть тоннаж сливов в короба быстро растет с уменьшением количества ковшей. Кроме того (на

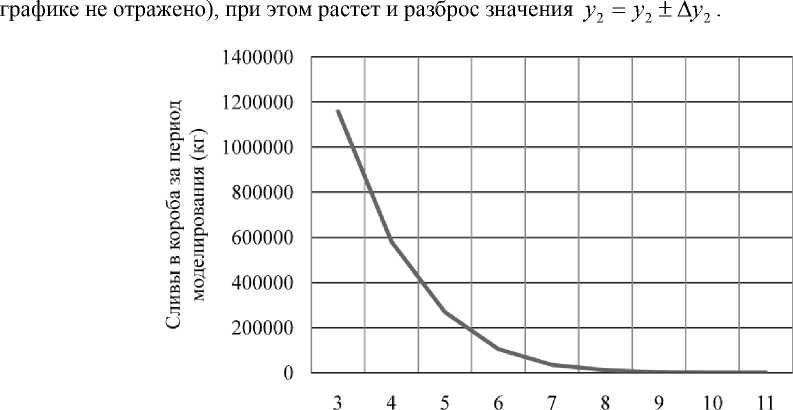
Количество донных ковшей (шт. )

Рис. 2. Зависимость среднего тоннажа слива в короба от количества донных ковшей

При значениях x1 < 6 изменениями других факторов не удается достичь исключения сливов в короба, во всем диапазоне возможных значений x2…x8 вероятность необходимости слива остается положительной. При x1 = 6…8 изменение других факторов модели позволяет иногда добиться нулевой вероятности сливов, что подробнее изложено ниже. При x1 > 8 вероятность сливов в короба можно считать исчезающе малой. Количество донных ковшей влияет также на другие реак- ции модели. Так, среднее ожидание в очереди на слив хлорида магния в ОПУ-3 меняется почти линейно y3 ≈1500 – 84∙x1 с высоким коэффициентом корреляции R2 = 0,91. Это хорошо соотносится с данными других авторов о том, что даже в больших системах массового обслуживания (СМО) времена ожидания изменяются линейно в зависимости от производительности, если задано равномерное распределение. Как известно, теорема Колмогорова для времени ожидания в очереди дает нелинейную зависимость [13], однако она справедлива только для экспоненциального и нормального распределения. В данном случае количество измерений было вынужденно произведено не настолько объемным, чтобы по результатам можно было бы определить и статистическое распределение тоже. Поэтому для пробных расчетов выбрали наихудшее, в некотором смысле, равномерное распределение, а переход к распределениям других видов исследовали отдельно.

Путем экспериментов определили, что на средние реакции модели практически не влияют вариации факторов x 2 , x 4 , x 6 . Интересно, что при этом увеличение x 4 вызывает увеличение разброса реакций Δ y 2 и Δ y 3. Рост фактора x 5 с 1,75 до 7,5 мин вызывает линейный рост y 2 , но практически не влияет на y ₁ и y ₃ (а только на Δ y ₁ и Δ y ₃). С увеличением и уменьшением фактора x ₇ реакции модели тоже практически не изменяются. При среднем времени монтажа аппарата восстановления, равном 45 мин, слив в короба – 20 567 кг за период моделирования, а при 95 мин – 38 033 кг. При этом на общую производительность ОПУ-2 y 1 этот фактор влияет ожидаемо линейно. Кроме того, данный фактор все же непросто изменить, так как есть определенные нормы и технические инструкции, и сокращение времени монтажа вызовет значительные изменения в сопряженных процессах производства. При увеличении времени слива x 8 количество сливов в короба растет сверхлинейно с показателем порядка 1,5. При количестве донных ковшей 7 и среднем времени слива, равном x ₈ = 1,5 мин, получаем количество сливов y ₂ = 2273 кг, а при x ₈ = 4 мин сливы в короба достигают y ₂ = 109 т, то есть примерно треть всех сливов участка.

В итоге, можно сделать вывод, что основными управляемыми факторами для дальнейшего исследования являются следующие:

• 1)    количество донных ковшей ( х 1 );

• 2)    время транспортировки донного ковша в 31-й цех ( х 5 );

• 3)    время слива хлорида магния в донный ковш ( х ₈).

Для них были произведены совместные изменения факторов попарно. Установлено, что совместное изменение x ₅ и x ₈ оказывает большее влияние на сливы в короба, чем независимое (см. таблицу).

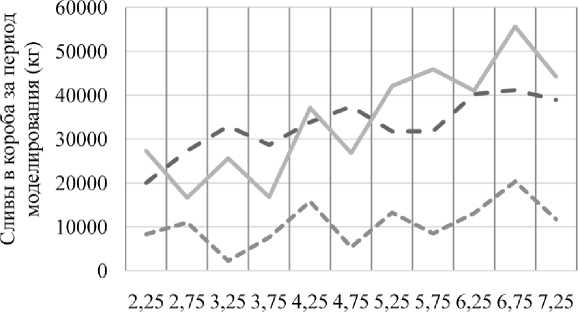
По описанной выше схеме счета на установление произведено несколько десятков вычислительных экспериментов (то есть десятков тысяч прогонов модели). Обнаружено, что устойчивая граница значений факторов, при которых вероятность сливов в короба становится чрезвычайно малой, находится в окрестности x 1 ≥ 8, x 2 ≤ 3…3,5 мин, х 3 ≤ 2,5…3,5 мин. Усредненный тоннаж сливов в короба y 2 при х 3 = 2,5…3,5 мин приведен на рис. 3.

Найдены условия, при которых сливы в короба уменьшаются до нуля, но при этом производительность участка восстановления и время ожидания слива в электролизер практически не меняются по сравнению с исходными значениями. При этом достаточно установления следующих значений факторов:

• •    количество донных ковшей x 1 = 9;

• •    уменьшение среднего времени транспортировки донного ковша x ₅ до 225 (с);

• •    уменьшение среднего времени слива хлорида магния в донный ковш за счет роста давления аргона в аппарате до x 8 = 162 с.

Как отмечено выше, для исследования достаточно произвольно выбрано равномерное распределение случайных величин. Исследуем, как изменится результат при переходе к другим распределениям. Например, при так называемых редких событиях , происходящих в СМО, их принято моделировать распределением Пуассона:

λ ^k

P (Z = k ) = I! eXP ^-^^, где λ – математическое ожидание, k = 0, 1, 2… – носитель распределения. Этим распределением хорошо описывается количество обращений в справочную службу, количество дефектов в потоке однородных изделий (или в одном протяженном изделии, наподобие рулона ткани), количество изюминок в выпечке и т. д. При количестве донных ковшей x1 = 7 зависимость сливов в короба от распределения среднего времени слива различная (рис. 4). Здесь принят носитель распределения k =2.

Очевидно, что до некоторого периода статистика сливов почти не зависит от вида распределения, однако при увеличении математического ожидания более «плотное» вокруг среднего значения λ распределение Пуассона начинает оказывать влияние на реакцию модели.

Результат при совместном изменении времени транспортировки донного ковша х 5 и времени слива хлорида магния в донный ковш x 8

Среднее время транспортировки донного ковша в 31-й цех (мин)

д н к о к Дч о Д о	Значения факторов модели модели							Результат моделирования
	Я >д а m о к X о д о и н о о у Д 1=5 S	Д М X 2 д' д Д )Д S ” дч а д * 5 £ д о д	д Д X Д Д а >д и Рч м . ю О о о д	д д о д д о д д д о о д д о Дч и	fct s s a —- § 1 О щ Д Д S ° Дч . « д а S	X К) m § А о 2 Д Дч w S	д о о д д о о Д о Дч и	н д о ю к	д д Д 5 со к д Д д S ю ° к ^ и	Дч О д 2 Д « ^ ю д ю д ^ 0J '^ д о
Начальное значение	7	4,5	5	4,75	2,5	3,5	3	881,3	37416	11146
1	7	4	4,5	4,25	2,2	3,2	2,7	883,1	23453	12413
2	7	3,5	4	3,75	1,9	2,9	2,4	883,9	14599	12240
3	7	3	3,5	3,25	1,6	2,6	2,1	879,6	2722	10656
4	7	2,5	3	2,75	1,3	2,3	1,8	879,3	2215	14328
5	7	2	2,5	2,25	1	2	1,5	884	906	13766
6	7	5	5,5	5,25	2,8	3,8	3,3	883,4	48923	12024
7	7	5,5	6	5,75	3,1	4,1	3,6	883,9	55246	13046
8	7	6	6,5	6,25	3,4	4,4	3,9	880	86596	11779
9	7	6,5	7	6,75	3,7	4,7	4,2	883	123784	8150
10	7	7	7,5	7,25	4	5	4,5	883	170876	8885

• - - Количество донных ковшей = 7

Количество донных ковшей = 6

• — — — Количество донных ковшей = 8

Рис. 3. Зависимость сливов в короба от совместного изменения количества и времени транспортировки донных ковшей

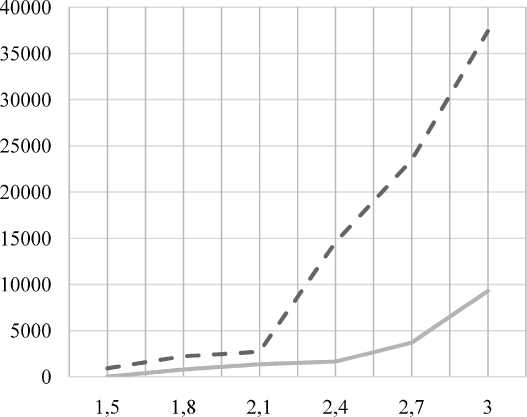
Среднее время слива хлорида в донный ковш (мин)

— — Сливы в короба при равномерном распределении Сливы в короба при распределении Пуассона

Рис. 4. Влияние выбора вида статистического распределения на y 2

Таким образом, цель, поставленная в данной статье, достигнута . Построенная и оснащенная авторами ранее имитационная модель совместной работы участков электролиза магния и восстановления губчатого титана филиала «Ависма» дополнена средствами организации вычислительных экспериментов (счета на установление). С ее помощью исследовано влияние на критически важные результаты работы системы восьми потенциально управляемых факторов из 46. Показано, что с точки зрения исключения сливов в короба наиболее значимыми являются три фактора: количество донных ковшей, время транспортировки донных ковшей и время слива хлорида магния из аппарата восстановления. Обнаружено, что их совместное изменение дает синергетический эффект, существенно превышающий эффект от независимого изменения значений факторов. В первом приближении определены границы значений факторов, при которых сливы в короба исключены. Следует отметить, что исследование вынужденно базировалось на достаточно ограниченном количестве натурных измерений, и для количественного уточнения результатов может понадобиться их расширение, хотя качественные результаты сомнения не вызывают.