Модельные представления процесса распылительной сушки фильтрата спиртовой барды на основе уравнений Навье-Стокса

Распылительная сушка растворов или суспензий является одним из наиболее распространенных методов производства широкого спектра порошкообразных продуктов в химической, пищевой и фармацевтической промышленности. В сушильных башнях распылительных сушилок контакт между каплей и тепловым агентом осуществляется прямоточно или противоточно. Наиболее предпочтительным для сушки термочувствительных материалов, таких как фильтрат барды, является прямоточный тип. Тепловой агент вступает в контакт с каплями в верхней части башни, где они имеют максимальную влажность при температуре мокрого термометра, при этом агент теряет большую часть тепла испаряя влагу.

Разработке математических моделей процесса распылительной сушки посвящены ряд работ отечественных [1–3] и зарубежных [4, 5] авторов. Однако, моделирование представляет собой сложную задачу процесса теплоотдачи при сушке капель жидкости. Помимо этого, следует учитывать ряд взаимодействий между самими каплями (слияние капель, агломерации и разрушение); между каплями и стенками при осаждении капель на стенках. Из–за сложности этих взаимодействий моделирование распылительной сушки проводится на основе теории вычислительной гидродинамики (CFD) [6].

Экспериментальная часть работы выполнялась на экспериментальной распылительной установке (рисунок 1).

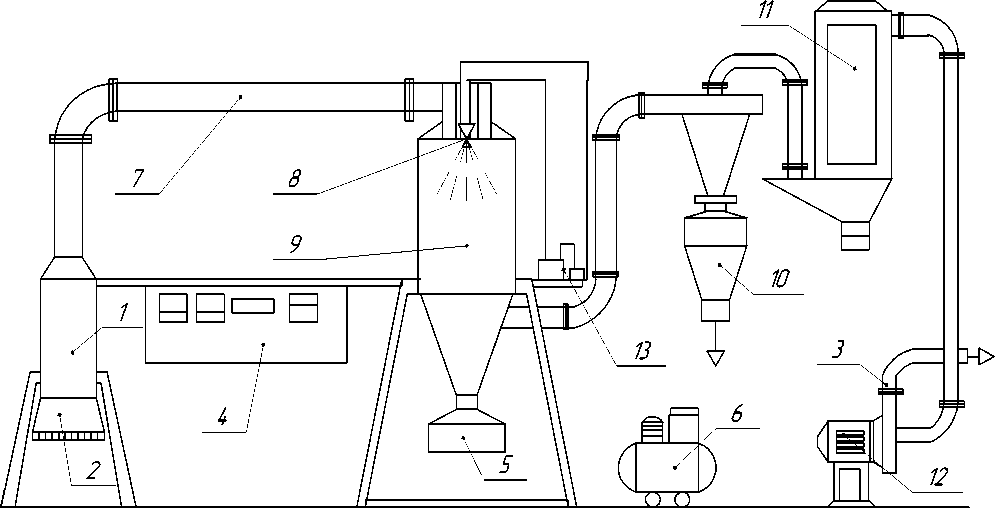
Рисунок 1. Схема лабораторной распылительной установки

Сушильный агент, посредством вентилятора 12, забирается из окружающей среды, очищается в воздушном фильтре 2, нагревается в калорифере 1 и по трубопроводу греющего агента 7 подается в камеру распыления 9. Одновременно, насосом 13 распыливаемый фильтрат барды подается в форсунку 8, которая создает равномерный факел распыла по сечению камеры и где контактирует с сушильным агентом с температурой 373–393 K . Высушенный продукт отводится в сборник 5, отработанный сушильный агент подвергается очистке от взвешенных частиц в циклоне 10 и через контрольную камеру 11 отводится в атмосферу.

В течение процесса сушки контролировалась температура на входе и выходе распылительной сушилки. Визуально через смотровое окно, оценивалось качество получаемого порошка.

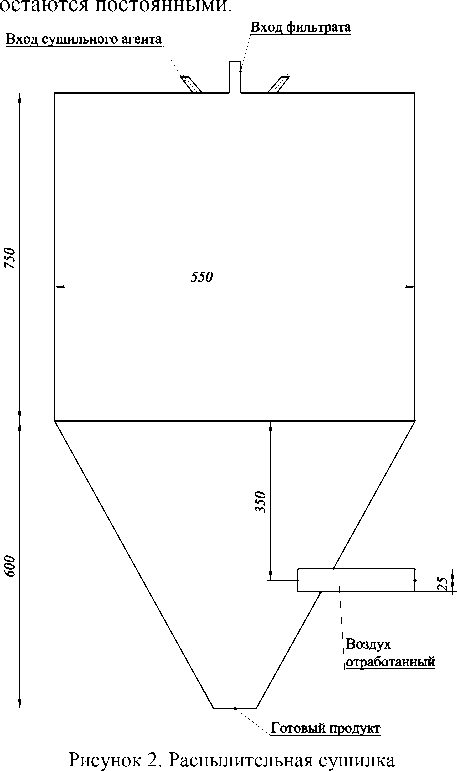
Цилиндро – коническая распылительная сушилка с техническими параметрами (см. таблицу 1) изображена на рисунок 2.

Т а б л и ц а 1

Параметры сушки

Параметр	Значение	Ед. изм.
Температура воздуха на входе в распылительную сушилку	373–393	K
Температура воздуха на выходе из распылительной сушилки	50	K
Расход жидкости на распыление	9,6×10-4	м3/ч
Давление сжатого воздуха	150	кПа
Расход сушильного агента	30	м3/ч
Время сушки	3-10	с
Дисперсность готового продукта	0,2-1	мм

Система уравнений, решаемых в программе ANSYS CFX представлена в виде нестационарных уравнений Навье-Стокса в неразрывном виде.

Мгновенные уравнения массы, момента и энергии для многокомпонентной системы можно записать в общем виде:

для массы:

p+ + V ( p v ) = 0,            (1)

для момента:

a(pv) +V( pvxv ) = -Vp + Vc + Sm , (2) a t и для энергии:

J -^ ^+V < P vJ ) = ^V( L ^V T ⁾⁺  (3)

■Mm) + vSM, тензор напряжения с в уравнении (2):

3            T 2 А с = plVv + (Vv) -—5Vvl,      (4)

где p - плотность компонента системы, кг/м3; t - время, с; v - скорость потока, м/c; J – энтальпия при постоянном давлении, кДж ; L – удельная теплота парообразования, Дж кг ; T - температура, K; р - динамическая вяз кость, Па • с ; 5 - толщина граничного слоя, м; V (vc) в уравнении (3) определяет вязкость; vSm – работа внешних сил (не учитывается);

T _н – вектор напряжения.

Для двухкомпонентной смеси, состоящей из капель фильтрата барды ( i ) и сушильного агента ( j ) (члены уравнения без индексации относятся к смеси в целом), уравнения переноса решаются в зависимости от скорости, давления, температуры и других свойств компонентов.

В скалярном виде они представлены следующим образом.

для массы:

+£(рЛ)

at     8 xj для массовой доли:

^a ( P Y ) + ^a ( ^p v j Y ) = a ³ D aY i ' at   ⁺   a_Xj      ax^ ‘ a _Xj _V

где x – горизонтальная координата; Y – массовая доля компонента; D – коэффициент диффузии, м² с.

Для упрощения решения задачи (1) – (6) принималось, что компоненты образуют идеальную смесь, свойства которой рассчитывались непосредственно из свойств компонентов и их пропорций. Дополнительные упрощения: капли имеют сферическую форму, плотность и удельная теплоемкость раствора и коэффициент диффузии паров в газовой фазе усреднены

При решении такого рода задач, как правило [6], переходят к уравнениям неразрывности для смеси компонентов.

для энергии:

^(pj)-5p. d (pr/) = д г ’ a t axjv J ’

=Af l dL+^Dj‘ 5Y+P. aj А axj / axj ■*    axj Ргт axj v

для тепловой диффузии:

A(pj)-ap . a (pvJ = a t( ) a t axjv J , a / l p А aj + axjL/ с Ргт J axj

где p - давление, Па; N _K - число капель;

C – теплоемкость при постоянном давлении, кДж K ; Pr – число Прандтля; нижний индекс т – параметр зависящий от турбулентности су- шильного агента.

Турбулентность оказывает существенное влияние на характеристики потока, и проявля-

ется, когда силы инерции в жидкости становятся значительными по сравнению с силами вязкости,

что характеризуется высоким значением числа Рейнольдса [7]. В этом случае модель к - е турбулентности задается уравнениями:

д ( р к ) д t

+ V ( p vk ) = V ц + ^ т- V к О к

д( ре)      ,     ,

+ V ( p v e ) = V д t

- ре ,(9)

Задача (7) – (11) решена методом конечных объемов. Понятие «конечный объем» относится к небольшому объему, окружающему каждую точку узла на сетке. Уравнения в частных производных преобразуются в поверхностные интегралы, используя теорему дивергенции [8]. Входные параметры задачи [9] представлены в таблице 2

Т а б л и ц а 2

ц + ^Ц ^ |V e

I    Ок)

+

+ к ( Се1 - Се 2 Ре ), где k – кинетическая энергия турбулентности, м2/с2 ; е - скорость диссипации вихревой турбулентности, м2/с3 ; Се1, Се2, ок, ое - константы.

Модель турбулентности имеет ограничение при прогнозировании логарифмического профиля скорости вблизи стенки. Поэтому было привлечено уравнение потока вблизи стенки:

v ⁺ = ^ = -ln ( у + ) + С , v_T   К ^{х 7}

y ₊ = p V y V r

Ц ’

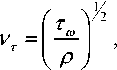
Входные параметры задачи

Параметры фильтрата барды
Удельная теплоемкость частиц	2050	Дж/кг⋅K
Удельная теплоемкость фильтрата	2600	Дж/кг⋅K
Удельная теплоемкость пара	1900	Дж/кг⋅K
Плотность фильтрата	1085	кг/м3
Скрытая теплота парообразования	2.26 × 106	Дж/кг
Коэффициент диффузии влаги	3,0 × 10-11	м2/с
Коэффициент диффузии пара	2,6 × 10-5	м2/с
Параметры сушильного агента
Температура	373	K
Массовый расход	30	м3/ч
Параметры стенки
Толщина	0,008	м
Теплопроводность	18,8	Вт/м⋅K

где v⁺ - скорость рядом со стенкой, м/с; v_T - скорость трения м/с; v _т - тангенциальная скорость к стенке на А у (м) расстоянии от

стенки, м/с; у ⁺ - безразмерное расстояние от

стенки; о сд - напряжение сдвига стенки, Па; к - постоянная Кармана [7]; С - постоянная зависящая от шероховатости стенки.

Получены профили распределения скоростей (рисунок 3) , температуры (рисунок 4) сушильного агента и влагосодержания капель фильтра барды (рисунок 5) от геометрии распылительной сушилки. Анализируя поведение капель, приведённых н а рисунок 3 – 5, можно сделать вывод, что мелкие капли концентрируются вблизи оси сушильной камеры где они быстро высушиваются, причем их температура быстро приближается к температуре сушильного агента. В то же время, из–за большей инерции, более крупные капли движутся по направлению к периферии камеры с сохранением значительного количества влаги.

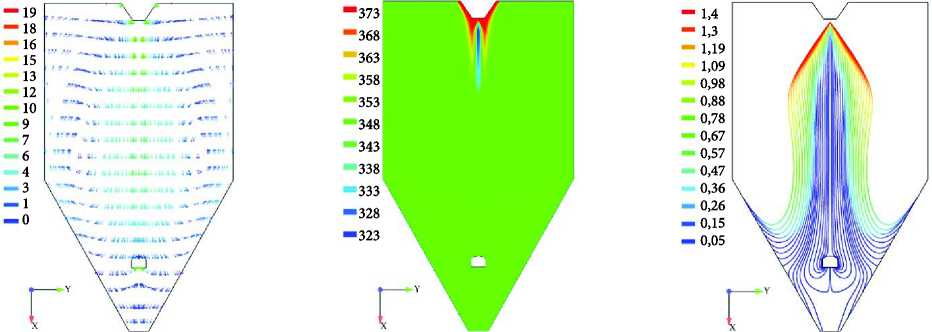
Рисунок 3. Профили скоростей Рисунок 4. Профили распределения Рисунок 5. Влагосодержание ка-сушильного агента              температуры сушильного агента        пель фильтрата, кг/кг

Мелкие сухие частицы покидают камеру через патрубок отвода отработанного сушильного агента; сухие частицы со средним размером, собираются в сборнике продукта; а тяжелые частицы ударяются о коническую стенку камеры. При этом некоторые из частиц после удара о стенки следуют к низу сушилки, а другие поднимаются в вверх камеры и затем уносятся потоками воздуха вниз.

Для проверки результатов моделирования поставлен ряд параллельных опытов по