Модельный подход к изучению свойств аморфных сплавов в области стеклования

Автор: Мантатов В.В.

Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths

Рубрика: Математическое моделирование и обработка данных

Статья в выпуске: 2, 2025 года.

Бесплатный доступ

Некоторые количественные характеристики аморфных и стекло- образных материалов, а также металлических стекол, несмотря на их структурное разнообразие, приблизительно совпадают. К примеру, энергия процесса возбуждения кинетической единицы, влияющей на процесс текучести. Примерно одинаковую величину для этих систем в твердой фазе имеет относительный флуктуационный объем, образовавшийся при температуре стеклования. Модель делокализованных атомов, основанная на предлагаемом механизме флуктуации атома с образованием вакансии, использует понятие флуктуационного объема в равнозначном смысле флуктуационному свободному объему. Такая модель позволяет исключить расхождения и недостатки, свойственные флуктуационному свободному объему в интерпретации ряда экспериментальных фактов.

Еще

Область стеклования, модель делокализованных атомов, относительный флуктуационный объем, металлические стекла, неорганические стекла, аморфные материалы

Короткий адрес: https://sciup.org/148331884

IDR: 148331884 | УДК: 51-72 | DOI: 10.18101/2304-5728-2025-2-41-49

Текст научной статьи Модельный подход к изучению свойств аморфных сплавов в области стеклования

Концепция модели делокализованных атомов основана на предложенном механизме критически амплитудного движения кинетической единицы (атома, группы атомов) при соответствующем ее возбуждении. Максимальное значение силы межатомного (межчастичного) притяжения, вызывающее наибольшее смещение атома (группы атомов) или делокализацию атома, возникает при флуктуации взаимодействия с внешними атомами [1; 2]. Подобные кинетические единицы были названы «делокализованными атомами». Например, в силикатных стеклах в роли «делокализованного атома» выступает мостиковый атом кислорода во фрагменте кремнийкислородной сетки Si-O-Si, а в аморфных полимерах — небольшой участок основной цепи макромолекулы (группа атомов в повторяю- щемся звене). Применяемая модель, модель делокализованных атомов, следует из обобщения теории флуктуационного свободного объема [3-5].

Флуктуационный объем стеклующейся системы, вызванный критически амплитудными смещениями делокализованных атомов из равновесных положений, служит существенным критерием модели

AVe = (ПГ2АГт )Ne = Ne^e , где Ne — число возбужденных кинетических единиц, nr — площадь сечения атома, Arm — критически амплитудное смещение делокализованного атома, Ave — элементарный флуктуационный объем, требуемый для процесса делокализации атома:

A v_e = n r ² А r_m .

Согласно термодинамической теории флуктуации плотности и модели делокализованных атомов можно утверждать, что относительная часть флуктуационного объема системы f = ΔVe

V связана со среднеквадратичным значением относительной флуктуацией плотности [6] следующим образом:

f = v Δρ

^A ve \ Р /

Здесь v=V/N — объем, приходящийся на кинетическую единицу.

При отсутствии в аморфной среде флуктуации плотности 2

А Ар / р} = 0 флуктуационный объем будет равен нулю V e =0. Включая вышеуказанную, а также ряд иных причин, флуктуационный объем не совпадает со свободным объемом жидкостей и стекол (при традиционном понимании последнего) [3; 6], иначе с объемом межатомного пространства [2].

Данная работа ставит своей целью определение значений относительного флуктуационного объема и ряда параметров модели для металлических стекол (аморфных сплавов) и сравнение полученных результатов с данными для аморфных полимеров и неорганических стекол.

1 Результаты расчета и их обсуждение

В теории стеклования имеется известное уравнение Вильямса — Лан-дела — Ферри (ВЛФ) [4], описывающее температурную зависимость времени релаксации и вязкости в области стеклования ln aT = - C1

T - Tg

T - Tg + C2

где т (T) и n (T) — время релаксации и вязкость соответственно, aT =т (T)/т (Tg)=n (T)/n (Tg) — их отношения температурных зависимостей со- ответственно. Сопоставление этого уравнения с уравнением, полученным в рамках данной модели [2]

ln a_T =

1 Т - Tg .

f,T - T + f в, g gg

где P _f = ( df / dT ) _T — коэффициент теплового расширения относительно

го флуктуационного объема при температуре стеклования, приводит к тому, что связь между C i и C ₂ — эмпирическими константами уравнения ВЛФ и относительным флуктуационным объемом — параметром модели делокализованных атомов, выглядит следующим образом:

Ci = 1/fg,

C2 = fg / в f .

Если обратиться к уравнению Фогеля — Фулчера — Таммана (ФФТ),

П = П о exp

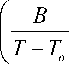
где B и T o — эмпирические константы уравнения, определяемые путем подгонки исходя из свойств материала, то видим, что константы этого уравнения и уравнения ВЛФ взаимосвязаны следующим образом [5]:

C = —B—, с2 = ts - T.

^{1 2} go

^Tg ^- ^To

Используя выражения (1), (2) и (3), можно рассчитать f g и P f по параметрам уравнения ФФТ

Т - Т h = , , в = 1/B .

В таблице 1 приведены параметры уравнения ФФТ для металлических стекол, взятые из работы [7].

Таблица 1

Температуры плавления T m , стеклования T g и коэффициенты уравнения

Фогеля — Фульчера —Таммана для металлических стекол [7]

Аморфный сплав	T m , K	T g / T m	T g , K	Коэффициенты уравнения Фогеля — Фульчера — Таммана
Аморфный сплав	T m , K	T g / T m	T g , K	η o , кПа·с	B , K	T o , K
Ni	1 725	0.25	430	2.0	4 700	295
Ni 62.4 Nb 37.6	1 442	0.66	945	0.49	5 380	810
Ni 75 Si 8 B 17	1 340	0.58	782	2.53	4 280	670
Fe 91 B 9	1 628	0.37	600	14.1	4 635	513
Fe 89 B 11	1 599	0.40	640	8.53	4 625	515
Fe 83 B 17	1 448	0.52	760	3.3	4 630	638
Fe 41.5 Ni 41.5 B 17	1 352	0.53	720	3.78	4 500	601
Fe₇₉Si₁₀B₁₁	1 419	0.58	818	1.9	4 505	701
Fe 80 P 13 C 7	1 258	0.59	736	2.25	4 600	616
Pd 82 Si 18	1 071	0.61	657	6.32	3 730	557
Pd 77.5 Cu 6 Si 16.5	1 015	0.64	653	2.57	3 820	553
Pd 40 Ni 40 P 20	916	0.66	602	1.5	3 600	509
Pt₆₀Ni₁₅P₂₅	875	0.57	500	5.31	3 560	405
Te	723	0.40	290	0.13	3 790	198
Co 75 Si 15 B 10	1 393	0.56	785	2.87	4 190	675
Ge	1 210	0.62	750	18.3	1 930	700

В таблице 2 показаны параметры модели делокализованных атомов, вычисленные по данным работы [7].

Таблица 2

Параметры уравнения ВЛФ и модели делокализованных атомов для металлических стекол (использованы данные [7])

Аморфный сплав		C 1	C 2 , K	f g	β f ·10⁴, K^-1	β f T g	Δε e	U ∞	U g (4)
							кДж/моль
№	состав
1	Ni	34.8	135	0.029	2.1	0.09	13	39	124
2	Ni 62.4 Nb 37.6	39.9	135	0.025	1.9	0.17	29	45	313
3	Ni 75 Si 8 B 17	38.2	112	0.026	2.3	0.18	24	36	248
4	Fe 91 B 9	53.3	87	0.019	2.2	0.13	20	38	266
5	Fe 89 B 11	37.0	125	0.027	2.2	0.13	19	38	197
6	Fe 83 B 17	38.0	122	0.026	2.2	0.16	23	38	240
7	Fe 41.5 Ni 41.5 B 17	37.8	119	0.026	2.2	0.16	22	37	226
8	Fe 79 Si 10 B 11	38.5	117	0.026	2.2	0.18	25	37	262
9	Fe 80 P 13 C 7	38.3	120	0.026	2.2	0.16	22	38	234
10	Pd 82 Si 18	37.3	100	0.027	2.7	0.18	20	31	204
11	Pd 77.5 Cu 6 Si 16.5	38.2	100	0.026	2.6	0.17	20	32	207
12	Pd₄₀Ni₄₀P₂₀	38.7	93	0.026	2.8	0.17	18	30	194
13	Pt 60 Ni 15 P 25	37.5	95	0.027	2.8	0.14	15	30	156
14	Te	41.2	92	0.024	2.6	0.07	9	31	99
15	Co 75 Si 15 B 10	38.1	110	0.026	2.4	0.19	24	35	248
16	Ge	38.6	50	0.026	2.3	0.39	23	16	241

Примечание: f g =1/ С 1 , β _f = 1/ C ₁ C ₂ , U ∞ = RC ₁ C ₂ , где U ∞ — свободная энергия активации вязкого течения при высоких температурах ( T >> T g ), R — газовая постоянная.

Важно подчеркнуть, что независимо от структуры и химического состава относительный флуктуационный объем в аморфных металлических сплавах, зафиксированный при температуре стеклования, сохраняет свое значение, которое примерно совпадает с относительным флуктуационным объемом для аморфных органических полимеров и неорганических стекол (табл. 3).

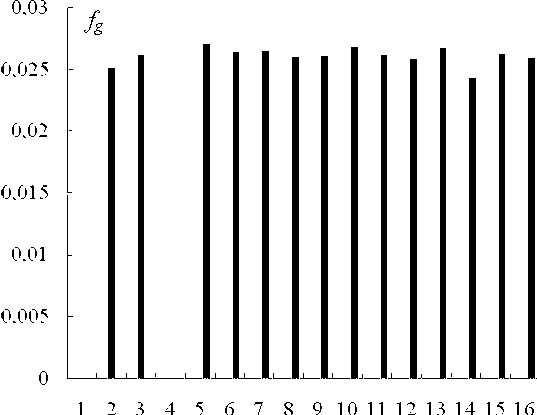
Рис. 1. Значения относительного флуктуационного объема аморфных сплавов из табл. 2. В рисунок не включены материалы № 1 и 4

Таблица 3

Константы уравнения ВЛФ и параметры теории флуктуационного свободного объема для аморфных полимеров и неорганических стекол [2; 4; 5]

Стекло	т T g , K	С 1	С 2 , K	f g	β f ·10⁴	Δ β ·10⁴	Δε e	U ∞	U g (4)
					K^-1		кДж/моль
Поливинилацетат	305	35.9	46.8	0.028	5.9	5	9.2	14	91
Натуральный каучук	300	38.4	53.6	0.026	4.8	4	9.2	17	96
Метакрилатные по-
лимеры:
этиловый	335	40.5	65.5	0.025	3.7	3	10.5	22	113
п -бутиловый	300	39.1	96.6	0.026	2.6	3	9.2	31	97
п -октиловый	253	37.0	107.3	0.027	2.5	2.5	7.5	33	78
Na 2 O-SiO 2
Na 2 O, мол. %
19.0	746	38	317	0.026	0.86	-	22.6	100	235
32.9	704	36	275	0.028	1.03	0.86	20.9	83	210
44.8	667	44	211	0.023	1.08	1.39	20.9	78	244
K₂O-B₂O₃
K 2 O, мол.%
0	578	29.6	121.4	0.034	2.9	-	16.3	30	142
2.1	586	29.7	89.0	0.034	3.8	-	16.5	22	144
8.5	623	33.4	116.9	0.030	2.6	-	18.4	32	173
23.5	712	36.0	140.4	0.028	2.0	-	21.2	42	213
34.4	701	38.4	142.1	0.026	1.8	-	21.2	45	223
Na 2 O-GeO 2

Na 2 O, мол.%
5	729	40.0	220	0.025	1.1	-	22.6	73	242
25	755	40.0	160	0.025	1.6	-	23.4	53	250
Na 2 O-PbO-SiO 2	761	32.2	280	0.031	1.1	1.0	22.1	75	203
Na 2 O-CaO-SiO 2	833	36.8	320	0.027	0.9	0.9	25.2	98	254
Se	303	32.4	57.7	0.031	5.4	2.7	8.8	15	81

Располагая сведениями об относительном флуктуационном объеме и температуре стеклования, можно рассчитать энергию процесса делокализации атома [1; 2]

Δεe ≅kTgln(1/fg).

Как видим, значения Δε e ≅ 12–25 кДж/моль энергии процесса делокализации атома для металлических стекол (табл. 2) и для неорганических стекол (табл. 3) приблизительно равны. По всей видимости, делокализация атома в металлических стеклах, как и в других стеклообразных системах [2], представляет собой низкоэнергетический мелкомасштабный процесс. Энергия активации вязкого течения при температуре стеклования U g = U ( T g ) для металлических стекол была вычислена по известному уравнению [8]

U g = C 1 kT g . (4)

Рассчитанные значения U g ≈ 120–250 кДж/моль (табл. 2) по порядку величины близки к данным для неорганических стекол (табл. 3). Значения коэффициента теплового расширения флуктуационного объема металлических стекол (аморфных сплавов) около температуры стеклования (табл. 2)

βf =1/C1C2 ≈(2.0-2.8) ⋅10-4 K-1

совпадают с данными для калиевоборатных стекол (табл. 3). Величина этого коэффициента для ряда стеклообразных систем совпадает со скачком коэффициента теплового расширения Δβ при температуре стеклования (табл. 3) [4; 5].

Кроме выявленного постоянства f g ≈ const целесообразно исследовать некоторые универсальные эмпирические и полуэмпирические закономерности, установленные в области стеклования жидкостей и полимеров, к примеру, известное правило Симхи — Бойера [9]

ΔβTg ≈ const ≈ 0.1 .

Поскольку β f ≈ Δβ , можно проверить неизменность произведения β f T g для аморфных сплавов, представленных в табл. 2. Можно утверждать, что правило Симхи — Бойера β f T g ≈ const ≈ 0.13-0.17 выполняется для всех веществ, кроме ряда элементов (Ni, Te, Ge).

Для металлических стекол эмпирическое правило «двух третей» T g / T m ≈ 2/3 имеет место лишь в первом приближении (табл. 1).

В области физики аморфных полимеров и стекол наиболее часто используется понятие о другом свободном объеме. Это понятие имеет свои истоки в классических работах по теории жидкостей [10; 11], а именно в так называемой «дырочной теории» жидкостей. Ряд авторов этот объем называют флуктуационным [4; 5] или избыточным [12; 13] свободным объемом. Флуктуации молекул (кинетических единиц) в области стеклования образуют флуктуационный свободный объем, который обеспечивает подвижность молекул и играет доминирующую роль в молекулярнокинетических процессах, таких как вязкое течение жидкостей и аморфных веществ. Относительный флуктуационный свободный объем составляет около 2–4% [4; 5], что на порядок величины меньше доли геометрического структурно обусловленного свободного объема.

Заключение

В модели делокализованных атомов, где образование флуктуационной дырки возникает как результат делокализации отдельной кинетической единицы, объем, занимаемый этой дыркой (флуктуационный объем), будет соответствовать флуктуационному свободному объему — понятию, которое используется в теории свободного объема. При использовании предлагаемой модели делокализованных атомов термины теории флуктуационного свободного объема [2; 5] меняют прежний физический смысл. Например, размер дырки приобретает смысл объема делокализации кинетической единицы (атома, группы атомов), зависящий от ее размера и предельной деформации межчастичной связи. Число дырок соответствует числу делокализованных атомов.

Таким образом, флуктуационный свободный объем следует рассматривать как геометрический объем, сформированный в результате критических смещений атомов в процессе их делокализации.