Models and methods of optimal control of software and technical configuration of heterogeneous distributed information processing systems

Introduction. Heterogeneous distributed information processing systems (HDIPS) are information processing systems that are characterized by territorial distribution, a variety of software and hardware components and a heterogeneous nature of tasks being processed [1; 2]. Such systems are used in areas where it is necessary to receive and process primary data of a various nature in an automatic or automated mode. They combine computational nodes (CN) and data sources of various types, which make it possible to carry out the entire computation process in the system, from obtaining raw operational data obtained from one or several sources to delivering final information to decision-makers.

One of the HDIPS features as a class of systems is a heterogeneous nature of tasks simultaneously solved in the system. They may require various software and hardware resources, which increases the complexity of the most efficient software and hardware configuration choice. Due to the complexity of the HDIPS, a decisionmaking process for software and hardware configuration management is associated with a large amount of uncertainty, making decision-making on the design and modernization of the HDIPS software and hardware configuration laborious, and increases error probability. The number of HDIPS software and hardware configuration elements and permissible ways of connecting them into various structures, which perform computational functions, are great.

The more components a HDIPS contains, the higher the complexity of the interaction between them is, therefore special tools are needed to work with such a large amount of information.

Existing approaches are either intended for universal computing systems and do not take into account heterogeneity [3–7], or do not imply the possibility of changing the software and hardware configuration [8–10].

The inter-agency nature of some HDIPSs also complicates the system management. For example, in the event that a HDIPS was formed due to the merger of several departments or divisions, it is difficult to see the system “from above” without special tools, to assess its potential and the way to optimize the combined computing resource use by shifting from independent problem solving “old” subsystems to a shared computing space.

The aim of this work is to formalize the problem of HDIPS software and hardware configuration management. To achieve this goal, formalization of possible optimality criteria of HDIPS software and hardware configuration was carried out, a HDIPS model in terms of queuing theory was proposed, the problem of allocating HDIPS computing resources was formulated as a transport problem by the time criterion with atomic needs, the algorithm for its solution was proposed and its applicability boundaries were determined.

Optimality criteria for HDIPS software and hardware configuration. Software and hardware configuration is a set of functional parts of an information processing system, their software and connections between them, due to the main technical characteristics of these functional parts, as well as the requirements of the tasks to be solved [11].

The problem of HDIPS optimal configuration choice is the choice of such a set of CN P , which provides an acceptable level of the optimality criterion J for solving a set of computational problems E. In this case, the optimality criterion may differ depending on the purpose of a particular HDIPS [12]. Such criteria can be as follows:

• 1.    Minimizing the CN utilization factor average value:

• J ¹ = min ( utilasid ) .

• 2.    Minimizing the total time on problem solving in the system

• 3.    Minimizing the probability of returning problem with CN due to a lack of computing resources:

In this case, we can assume that the computational load is evenly distributed and there are no overloaded nodes

J2 = min(£T (ei) ) , where Т – time spent on problem solving ei , n – number of problems, calculated at the time of change. HDIPS can be used in areas where decision-making time is critical, in which case minimizing a problem processing time is more important than uniform load distribution.

n

J = min ^ ^ ip,._tiurnj .

In case of an incorrect combination of computational load, a number of CNs and algorithms for distributing the computing resource in the HDIPS, situations are possible when the task arrives at the CN, which does not have enough free resources to process it; in this case the task is returned to the routing agent. The likelihood of such returns must be minimized, since they indicate the non-optimal configuration of the HDIPS and increase the time spent on tasks in the computing system.

The choice of the efficiency criterion for the projected computing system is the first step in solving the problem of optimal HDIPS software and hardware configuration choice. To achieve the selected optimality criterion, it is proposed to analyze the HDIPS software and hardware configuration using its formal model, applying the queuing theory methods.

Representation of HDIPS in the form of a queuing network. HDIPS can be represented as a queuing network, where each СN and route control unit is a mass service system (QS). By a queuing network we mean a set of interconnected servicing devices with queues (queuing systems), in which requests pass from one device to another with a certain probability [13]. Each СN is represented as a multichannel QS without a queue, which returns a request for calculating a task to a routing agent if there is not enough computational resource for its execution.

Queues are accumulators for routing agents, while the probability of task transition to a specific CN is determined by the routing algorithm operation. A general scheme of the queuing network HDIPS is shown in fig. 1

The QS scheme of the CN is shown in fig. 2. Unserviced requests can arise in the QS of the CN in the event that upon the request receipt for the CN there is not enough resource to process it.

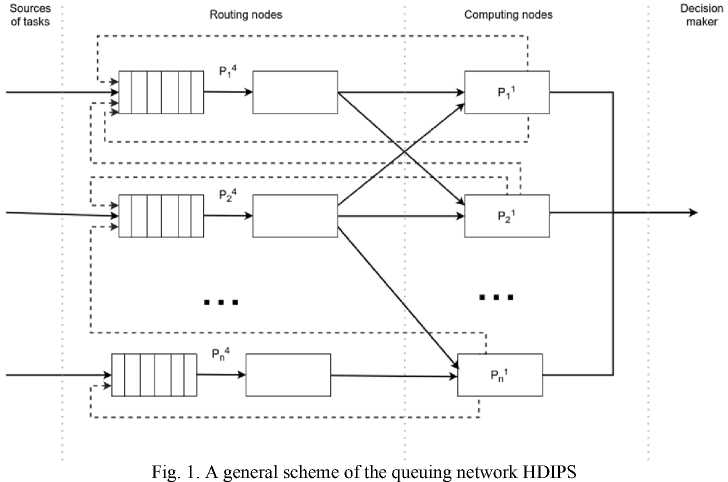
Рис. 1. Общая схема сети массового обслуживания ГРСОИ

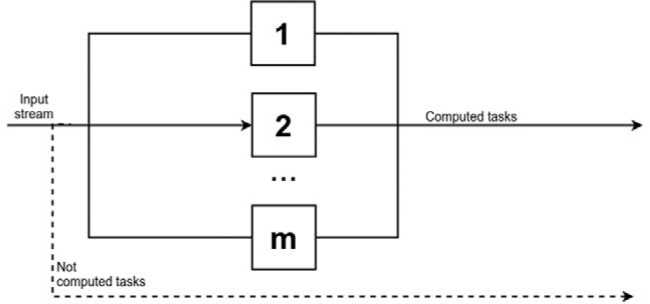
Fig. 2. The scheme of the queuing system computing node

Рис. 2. Схема системы массового обслуживания вычислительного узла

In this case, the probabilities of the task transition from the router p ⁴ i to the CN p ¹ j is defined as the product request probability sending to this node in accordance with the routing algorithm operation and availability of the necessary software coefficient aⁱ task in the software configuration of the control node a^j server .

Pj = p ^, where

[ 1, if CN j is provided with required software , k u = 1

[ 0, if CN j is not provided with required software.

For each task subset requiring the same software set, only a CNs subset will be available that satisfies the condition of suitable software availability.

Thus, for a task from the Aktask set, only a part of the queuing network elements will be available; therefore, it is advisable to calculate the average time spent on tasks in the system using the weighted average time spent in the task system for each type of software from Atask, subsets, where the weight will be the probability of the task appearance, requiring Aktask, software in the system. Thus, it is possible to represent the efficiency criterion J2 using the queuing theory instruments:

N

j 2=t=^Zwaa,

^л u = 1

where Л - total intensity of network input streams, t; j - average time spent by a task in j QS, Xj - input flow rate j QS, wi – weight of i task. To achieve the selected optimality criterion, in addition to enumerating different permissible combinations of software and hardware configurations of the system individual elements, it is necessary to determine the optimal algorithm for requests distribution for computations to computational nodes.

Transport task by the time criterion with atomic needs. The function that reflects the total time of data processing problems at any finite time interval is presented in the form of a transport problem according to the time criterion [14].

There exists m of starting points (SP) A 1 , …, A m with margin a 1 , …, a m and n of destination points (DP) B ₁, …, B_m with requests b ₁, …, b_m the sum of margins equals the sum of requests:

mn E ' E i = 1 j = 1

The times of transportation t_i j from each SP A_i to each DP B j are given, it is assumed that they do not depend on the amount of the transported cargo.

It is required to choose transportation ( x ij ) in such a way that the balance conditions are met

Exxj=a(i=i-,m), j=0

A

m

E xx j = ^b j ( ^j = 1,-mm ) , _ i = 0

and in addition, the end time of all transportations T turned at a minimum. Thus, it is necessary to find a transport plan ( x ij ) for which the time T turns into a minimum:

T = max t,, = min .

x ij > 0 ij

The described problem can be used to select the optimal route for computing problems at time t ⁰ as follows. Computing nodes will be software A ₁, …, A_m , and their free computing resource at the moment t ⁰ will be a stock in terms of transport problems. Moreover, each task will be a DP with a certain need for computing resources. This introduces an additional condition for transportation – each DP must be served by single software.

In order to support the heterogeneity of both computational tasks and software and hardware, computational tasks are considered as atomic – that is, indivisible between CNs. If a computation task is not atomic, it must be represented as a set of sequentially (or in parallel, depending on the nature of the task) of atomic applications running.

The condition on the atomicity of tasks introduces into the formulation of the transport problem the abovementioned restriction that each DP must be serviced by a single software; in what follows, this type of transport problem will be called a transport problem by the time criterion with atomic needs.

The atomicity condition makes it possible not to consider the combination of servicing the DP by several softwares, which significantly reduces the complexity of the solution algorithm in comparison with the classical solution of the transport problem by the time criterion.

The transportation time (in terms of the model, the processing time of the task) t ij is calculated as the sum of the task B j delivery time forecast to the node A i , the forecast of the calculation time, and the forecast of the delivery time of the received data to the destination.

If at time t ⁰ the computational task B j is being processed at the node A i , t ij will express the remaining processing time + the time of data delivery to the end point.

For other nodes, the processing time for this task will include the cost of transferring the calculation from the current node to another.

If the CN A i cannot process the task B j , for example, does not have the necessary software, then we assume that the processing time t_i j is equal to infinity.

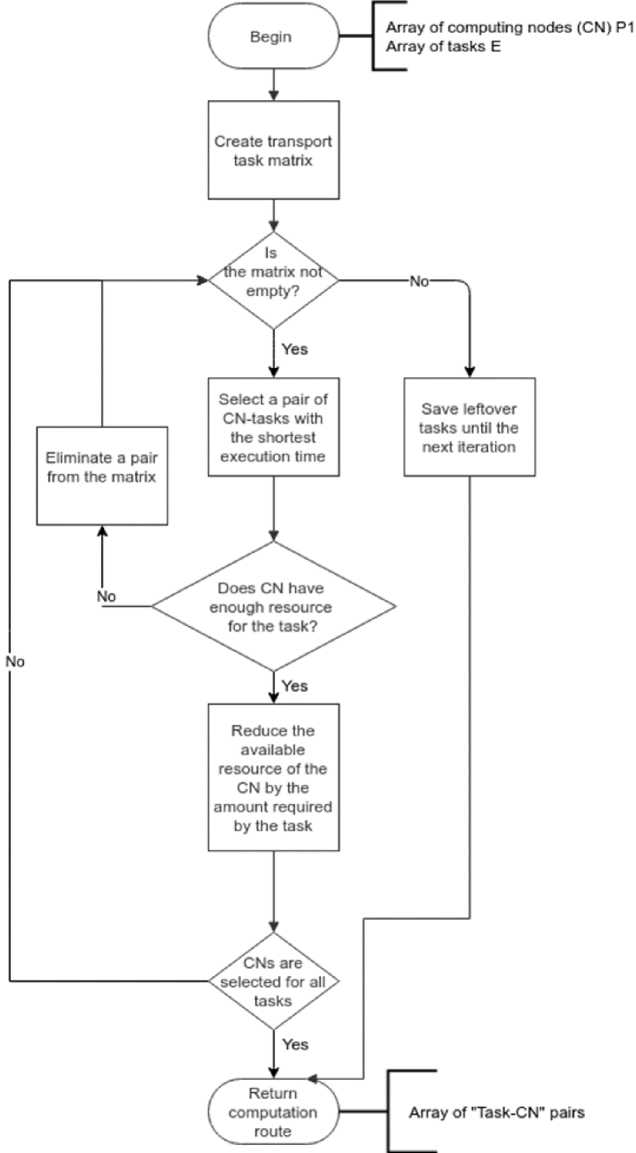
Least-time algorithm for atomic claims. The prob lem of choosing the most efficient computation route at time t ⁰ can be represented as a transport problem according to time criterion with atomic needs described above. Taking into account the condition that computational tasks are atomic, that is one task can be processed only on one node (in practice, this can be achieved by preliminary partitioning of complex calculations into a sequence of atomic tasks), the solution of a transport problem by the time criterion with atomic needs degenerate. The developed least-time algorithm for atomic claims (LTfAC) for the transport problem according to the time criterion with atomic needs can be represented as a diagram in fig. 3.

The algorithm works as follows. It is necessary to select a pair of DP and software with the smallest t ij , provided that the software has all the necessary resources to service the DP, and then adjust the stock for software by the amount of DP and repeat the selection until all DP are served, or until no software will be able to serve the remaining DP. In this case, tasks for which a suitable computational node is determined are sent for computation, and the remaining tasks wait for the next iteration of the algorithm.

The efficiency of the developed algorithm was investigated on the HDIPS simulation model [15]. Fig. 4 shows a graph of the average computation time of tasks in the HDIPS dependence on its structure when using the LTfAC algorithm as an algorithm for computing resources distribution in HDIPS. For clarity, the axes of CN number and the number of tasks sources on the graph are inverted.

The developed algorithm provides the minimum average time for tasks completion and this time is fairly stable relative to the number of CNs. Thus, the developed algorithm is recommended to be used if the advantage from reducing the time of tasks calculations exceeds the cost of additional HDIPS computational load, thus the J ² optimality criterion of the configuration is selected.

Conclusion. The following possible criteria for the optimality of the HDIPS software and hardware configuration were identified and formalized:

– minimizing the average value of the CN utilization factor;

– minimizing the total time for problem solving in the system;

– minimizing the probability of problem return with a CN due to a lack of computing resources.

To meet the selected optimality criterion it is proposed to analyze the HDIPS software and hardware configuration using its formal model applying queuing theory methods. HDIPS can be represented as a queuing network, where each CN and route control unit is a mass service system. In terms of the proposed formal model, a function is defined which expresses the probability of a task transition from a router to a computational node. The example of the presentation of the criterion “minimizing the total time of problem solving in the system” in the formal model using the apparatus of the queuing theory is given.

The problem of computing resource allocation in HDIPS is presented as a transport problem according to the time criterion with atomic needs. The atomicity condi- tion makes it possible not to consider the combination of serving one destination (in terms of the transport problem) by several starting points, which significantly reduces the complexity of the solution algorithm in comparison with the classical solution of the transport problem by the time criterion.

Begin ie matrix nol empty? ,

Does CN have enough resource for the task?

Return computation route

/DNs are\ .selected for all \_ tasks /

Array of computing nodes (CN> PI Array of tasks E

Yes

Array of "Task-CN" pairs

Yes

Yes

Reduce the available resource of the CN by the amount required by the task

Save leftover tasks until the next iteration

Eliminate a pair from the matrix

Create transport task matrix

Select a pair of CN-tasks with the shortest execution time

Fig. 3. Block diagram of the resource allocation algorithm via solving a transport problem by the time criterion with atomic needs using the LTfAC method

Рис. 3. Блок-схема алгоритма распределения ресурсов решением транспортной задачи по критерию времени с атомарными потребностями методом НВдАЗ

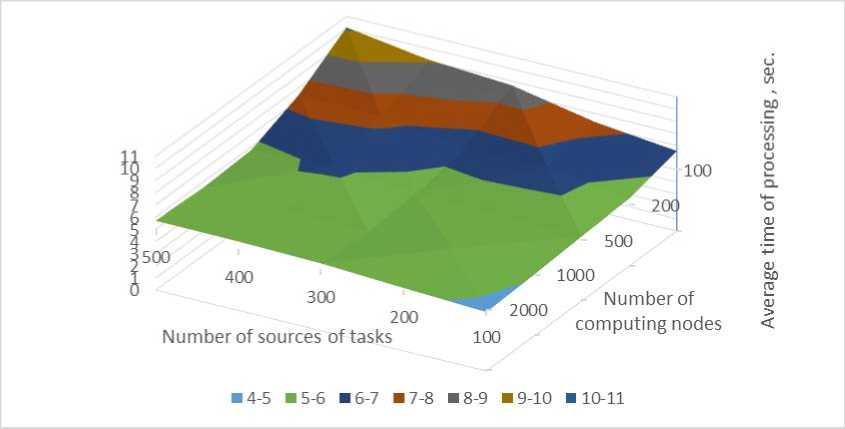
Fig. 4. Time of tasks processing when using the LTfAC algorithm for resource allocation

Рис. 4. Время обработки задач при использовании алгоритма НВдАЗ для распределения ресурсов

Taking into account the condition of atomicity, the least-time algorithm for atomic claims was developed. In comparison with other investigated algorithms, the developed algorithm provides the minimum average time for executing tasks and this time is fairly stable relative to the number of CNs. Thus, the developed algorithm is recommended to be used if the advantage from reducing the time for calculating the tasks exceeds the cost of the additional computational load of the HDIPS, that is, the criterion of optimality of the configuration “minimizing the total time for problem solving in the system” is selected.