Модифицированная формула Герасимова-Капуто

Д.Ф., Пастухов Ю.Ф. распространяется под лицензией CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите

В работе [1] показано, что в задачах аномальной диффузии необходимо использовать производные дробного порядка, принимающего значения на интервале (0,2). Другой пример, в задачах механики поток газа Трикоми на звуковой лини прямо пропорционален производной порядка 2/3 от функции тока [2]. Как известно, производная Герасимова–Капуто определяется [1], [2], [3], [4] интегральной формулой (1) .

В работе показано, что для явного вычисления производной Герасимова–Капуто необходимо еще одно слагаемое, которое зависит от значения функции u(0), переменной t и порядка дробной производной α на интервале (0,1). Данное слагаемое необходимо для согласования производной функции целого порядка и предельного значения производной дробного порядка, когда ее порядок становится целым. Для некоторых функций новое дополнительное слагаемое в точке t=0 не требуется, например, для функции u(t)=sin(t) в интервале α = (0,1). В работе максимально упрощен алгоритм вычисления дробных производных квадратурной формулой Гаусса. В программу вводится исходная функция, первая или вторая ее производные. Гладкости первого или второго порядка используемой функции требует также формула-определение (1).

В работах [5], [6], [10] рассмотрены разностные уравнения и аналог задачи оптимального управления Л.С. Понтрягина с производными дробного порядка.

Постановка задачи

Пусть заданная функция u(x,t) является достаточно гладкой по переменной t, u ( x, t ) e C n (0, t ) , тогда производная функции целого порядка n по переменной t является непрерывной и интеграл в формуле (1) сходится, так как в особой точке т ^ t знаменатель дроби пропорционален 1/ ( t - т ) ^а- ^{n + 1} учитывая - 1 <  а - n + 1 <  0 .

Определение 1. Производной дробного порядка α>0 Герасимова–Капуто от функции двух переменных u(x,t) (по переменной t ) [1], [2], [3] называется функция

( D ^а + , t ^u \x , t ) =

1 rd ⁿu ( x , т )      d r

Г ( n - а ) J    df   ( t - т ) ^а - n ^{+ 1}

n = [ a ] +1, n ^e Na ^e R , а - n +1 = { a } e ( 0,1 ) .

Для простоты рассмотрим частный случай дробной производной для функции одной переменной u(t) , так как в нашей задаче переменная x не используется. Для двух интересующих нас интервалов порядка производной с учетом формулы (1) получим:

• 1) . 0 <  a <  1, n = 1

( D a U\t ) = — j- du ^ r )         , n = 1,0 <  a <  1 (2)

V ⁰⁺, t Л >  г ( 1 - a ) J d _T   ( t - r ) ^{a ,      ,           1 7}

• 2) . 1 <  a <  2, n = 2

⁽ D •> ) ( ¹ ) =         J dur       ' " = 2, ¹ <  “ <  2 ' (3)

Г (2 a) 0 dr   (t - т)

Гамма-функция в формулах (2), (3) вычисляется по формуле Эйлера (4):

Г ( a ) = J t ^{a — 1} e‘dt , t e [0, ® ), a >  0 .        (4)

Поскольку дробные производные в формулах (2), (3) определены с точностью до множителя Г ( 1 - a ), Г ( 2 - a ) , то сложность вычисления производной дробного порядка заключается в сложности численного алгоритма для соответствующего интеграла. В языке FORTRAN вызовом функции dgamma( a ) Г ( a ) вычисляется с относительной точностью 10 ^{- 15}.

Очевидно, что производная дробного порядка α в (2), (3) должна переходить в производную целого порядка n -1 в случае a ^ n - 1 . Если в формуле (2) a ^ n - 1 = 0 , то

( D " и \<) = 4| j du T) dd'' = " ⁽ t ) - " ⁽⁰) ■ (5)

^{Г ( 1 )} 0 ^{d T (} t ^- T )

для a e (0,1) :

Г (1 - a )j

d" (t )  dr dT  (t - т)a

_     1

= Г ( 1 - a )

^f " (0)

-—+ lim f   £ _|>

V

" ( t - £ )

£

—

"^{( T} )  ‘ т .(9)

! ( t - т ) ^{a + 1}    jj^u

В формуле (9) под знаком предельного перехода два слагаемые, зависящие от переменной ε, стремятся к бесконечности, и именно их разность может дать конечное число. Уточняя формулу (7), получим

( D O S t ) =                    + — I ® e (0,1)( . (10)

^{0 + ,} t ^Л '   Г ( 1 - а )Ц d T ( t - т ) ^a     t ^a J ^{,                ;}

Преобразуем также (3):

1 r d²" ( t )    d r

Г ( 2 - a ) j dd  ( t - т У ^{- 1}

Аналогично, если в формуле (3) a ^ n - 1 = 1 , то

1 r d ² " T ) d T       d , d

⁽ D£"It )=7o f а Л  v-1 = ^ " ( t ) " (0) ■ (6)

Г ( 2 - 1 )* d r ( t - т )      dt       dt

Рассмотрим пример:

" ( t ) = sin( t ) : D _{0 +} ⁰ " ( t ) = sm( t ) - sm(0) = sm( t )

D a ^' ' " ( t ) = sin ( t ) - sin (0) = cos( t ) - 1 ^ cos( t ) ■

Получаем противоречие для производной синуса первого порядка и формулой (6) на интервале a e (1,2) , хотя противоречия для производной синуса нуль порядка на интервале a e (0,1) и формулой (5) нет.

Чтобы устранить противоречие, в формулу (2) нужно добавить слагаемое вида '■) t ) = Г й [ i dd r Zr ⁺ " ⁽⁰⁾ g '<' • ^{a )}} (7)

Сравнивая формулы (5) и (7), получим g j ( t , a ^ 0 + 0) = 1, a e (0,1) . Также добавим в формулу (3) слагаемое вида

\      1     | r d²" ( т )    ‘ т d           J ™

⁽ D 0 + , t " X t )       J кт/—ы ⁺ -т» (°) g 2⁽ t ^{, a} ) ⁽⁸⁾

Г ( 2 - а ) (• ‘ т ( t - т )      dt            J

g ₂ ( t , a ^ 1 + 0) = 1, a e (1,2) .

Преобразуем интеграл в формуле (2) по частям

1 ^f " ’(0)   _r

—,---г —¥+ lim

Г ( 2 - a )     t ^{a — 1}    £ ■

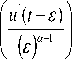
t —£

^{— ( a 11} j

"T. ^{( t — T a}

d r

. (11)

Аналогично формуле (10), для интервала (0,1) на интервале (1,2) получим модифицированную формулу Герасимова–Капуто (12):

1 <  a <  2, n = 2

( DI, t " ) ( t ) =

¹ ff ^{d 2}" ^{( t} )    ^{d T}

Г ( 2 - a )P d r ²   ( t - т a ^{— 1}

₊ " '^{(0 )} t^a - 1

Заметим, что формула (10) переходит в функцию "(t) при a ^+0, а формула (12)

переходит в производную

d" ( t ) dt

при a ^ 1 + 0 .

Определение 2. Модифицированной формулой Герасимова–Капуто на интервале 0 <  a <  1, n = 1 определим формулой (10), а на интервале 1 <  а <  2, n = 2 определим формулой (12) .

Определение 3. Модифицированной формулой Герасимова–Капуто на интервале n - 1 <  a <  n , n = [ a ] + 1 определим формулой

( D E7X t ) =

1 f^ d n " ( т ) d r        "^{(n ч}(0) 1

Г ( n — a ) V^j ~dF ( t - т ° ^{— n + 1} + t ^{a — n + 1} J

. (13)

Формула (13) переходит в формулу " ^{( n} 1) ( t ) при а ^ n - 1 + 0 .

Рассмотрим обобщение производной дробного порядка от степенной функции:

dkxn dxk

= n ( n - 1)...( n - k + 1) x" ^k

n!    _x — — k

( n - k )!

Для производной дробного порядка получим аналогичное выражение:

α

d ^a xⁿ

ri n   „n—a

---==----- x dX    ( n — a )!

Г ( П + 1)   _x — — a

Г ( n — a + 1)

.

Разложим гладкую функцию в ряд Маклорена, используя предыдущую формулу:

В работе [9] получена составная квадратурная интегральная формула с равномерным шагом и с 12 порядком погрешности O ( h ¹²), которую мы используем для первого интеграла в (17) на отрезке [0,b]

bn f u (x) dx = 5 h £ Ciu (xi) + O (h12 J n = 10 m, h =

b — a ----, m e N ,

n

X u ( t ) = £ n = 0

u ⁽ n ) (0) tⁿ

n !

₌ u⁽n ) (0) tn

=^£ Г ( n + 1)^,

если

( D . u i t ) = У Г ⁽ n ⁺ 1) u ^ =V

^{7 0 Л} n = 0 Г ( n — a + 1) Г ( n + 1) n = 0 Г ( n — a + 1)

i = 0 v i = n

( — 1) ^k

Для функции u ( t ) = cos( t ) = £ ^^ t ^{2 k} получим

X

У

Г (1 — a ) ^£

I                    \(¹⁴⁾

( D a + , t cos( t )H

X

£

Г (2 - a ) kl

( — 1) ^kt ^{2 k —a}

~2k

П ( i — a )

i = 1

/     k ,2 k — a

(—1) t t 2 k

П ( i — a )

i = 2

, a e (0,1)

. (15)

, a e (1,2)

( — 1) ^k

Для функции u ( t ) = sm( t ) = £ ^ ^ t^{2 k 1} имеем

X

У

Г (1 — a ) k = 0

/                  \(14)

( D . t sin( t )H

X

£

Г ⁽² - ^a ) k = 0

(  1) k ?2 k + 1 — a

2 k + 1

П ( i — a )

i = 1

/     k <2 k + 1 — a

(—1) t t 2 k+1

П ( i — a )

i = 2

, a e (0,1)

. (16)

, a e (1,2)

Опишем численный алгоритм, аппроксимирующий формулу (10), отбрасывая известный

1 множитель           и слагаемое

Г ( 1 — a )

Представим интеграл (2) в виде используя во втором интеграле переменных z |0__b = t — rj t , dz = — d r .

u ( o )

.

. ta суммы, замену

, ( i = 0mod10 ) A ( 0 <  i <  n )

149688 ,v                v        7

( i = 1mod10 ) v ( i = 9mod10 )

— 16175

( i = 2mod10 ) v ( i = 8mod10 )

( i = 3mod10 ) v ( i = 7mod10 )

5544 , ( i = 4mod10 ) v ( i = 6mod10 )

i = 5mod10

Вычислим второй интеграл в (17)

t г b u( t — z ) dz

J a

0       ^z

Предварительно введем вспомогательный интеграл с параметром a под аргументом функции:

т           , t f b u ( t + a — z ) dz

1 ₂( b , t , a , a ) = I                     .          (19)

0       ^z

t

I ^{( u (} t ^f

u ( r ) d r

к a

b

= f

u ( r ) d r

a a

t

+ f

b

u ( t ) d r _

a

_ b u ( r ) d r 0 ⁽ t ^{— r ) a}

—

0 I t — b

u (t — z)dz a z

_ b u ( r ) d r 0 ⁽ t ^{— r ) a}

t — b

+1

u ( t — z ) dz (17) z ^a

Для

максимального

упрощения

алгоритма, первую производную в (17) от известной функции считаем заданной.

Параметр a необходим для аппроксимации первой производной в (10) квадратурной формулой, которая в данной работе не используется, но получена в работе [9].

Весовая функция неотрицательна p ( z ) = ^E >  0 на отрезке [0, t — b ] . z ^a

Построим [8] квадратурную формулу Гаусса с тремя узлами.

Утверждение 1. Если функция u ( t )

непрерывно дифференцируема на отрезке [0,t-b] с весом p(z) = — > 0, z e [0,t — b], то za квадратурная формула Гаусса имеет вид

I u ⁽ t ⁺ a — z ) dz = C_u ( x ) + Cu ( x^ ) + Cu ( x ) + O ( ( t — b ) ⁶ ) , (20)

0       za где неизвестные C1, C2, C3, x1, x 2, x3 равны

C i =

( X j — x ₂ )( X j —

(ft ,                    J t ^{— b} )

-^-1 ⁽ t + a - X 2 ⁾⁽ t + a - X 3 У    ⁷

X 3 ) к                            (1 — a )

—

C 3

з           \ ( t — b ) ^{2 — a}   ( t — b ) )

— ( 2( t + a ) — x? ^_ x^ )-- 1--I,

³²⁷ (2 — a )    (3 — a ) I’

C 2

1	(
( x 1 — x 2 X x 2 — x 3 )	( t + a — x 3)( X j — t
	к

— a )

—

+ ( 2( t + a ) — X 1 — x 3 )•

( t — b )"- “

d— a

-——C -C

,      2 H ,

⁽1 ^— a )

( t - b r ₊

^{(1 — a} )

( t — b Г

(2 — a )     (3 — a ) I ’

.„= , ₊ a - ²       s 1 ]+1,

, bb?   (1 + 2n) b x 2 = t + a — 2, c°s    ^—l + J,

_Y 7 W 1 ^{+ 4 п} К ^b 1 x-> = t + a — 2-. — cos i------i +—,

³            v 3    \   3    7    3

( Z X

’1

—

1 = arcco;

= arccos

bc

— + d

A

—

к

2 f

•

В формуле (20)   b 1 , c , d

–

неизвестные

для

ортогонального полинома [8]:

P ( z ) = z ³ + bz ² + cz + d , p ( z ) =~7> 0, z e[0, t — b ], z

_b _ — 3(3 — a )( t — b )   _ 3(2 — a )(3 — a )( t — b )²

¹ =      (6 — a )    ’ c =     (5 — a )(6 — a )    ’

_d_ — (1 — a )(2 — a )(3 — a )( t — b )³ =     (4 — a )(5 — a )(6 — a )

•

Доказательство . Определим ортогональный полином

( t — b ) 4 — a   ,	( t — b ) 3 —	+ с ( t — b ) 2 — a	+ d ( t ~	<1 = 0
(4 — a )     1	(3 — a )	(2 — a )	(1-	)
( t — b ) 5 — a +b	( t — b ) 4 —	+ с ( t — b ) 3 — a	+ d ( t ~	b ) 2 —   = 0 • (22)
(5 — a )      1	(4 — a )	(3 — a )	(2	—   )
+ b	( t — b ) 5 — '	+ с ( t — b ) 4 — '	+ d ( t ~	b ) 3 —   = 0
(6 — a )      1	(5 —   )	(4 — a )	(3	—   )

Из системы (22) получим уравнения (23), (24):

( t — b )³ _+b     ( t — b )²        с ( t — b ) ₊        d         ₀

(4 — a )(2 — a )   ¹ (3 — a )(2 — a )  (2 — a )²  (1 — a )(2 — a )        ⁽²³⁾

'     ( t — b )³    _+b ( t — b )²          с ( t — b )    ₊        d

(5 — a )(1 — a )    1 (4 — a )(1 — a ) (3 — a )(1 — a ) (2 — a )(1 — a )

'   (t—b)3 +b (t—b)2    । с(t — b) +

(5 — a )(3 — a)   1(4 — a )(3 — a)  (3 — a )2  (3 — a )(2 — a )

'                + b,    (t—b)2    +               +       d=

(6 — a )(2 — a )    (5 — a )(2 — a )  (4 — a )(2 — a )  (2 — a )(3 — a )

Вычитая из вторых уравнений систем (23) и (24) первые уравнения в (23) и (24) соответственно, получим систему двух уравнений (25) с константами b 1 , c :

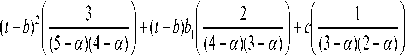
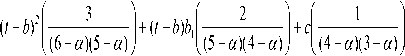
= 0

= 0

Второе уравнение в (25) умножим на дробь       , затем вычтем из полученного

^{(2 —} a )

выражения с множителем —--- первое

уравнение

3( t — b ) (        1 ___ 1    )

(5 — a ) [ (6 — a )(2 — a )  (4 — a )² J

2 b  (        11

(4 — a ) к (5 — a )(2 — a )  (4 — a )(3 — a )

= 0 о

z3 + bz2 + cz + d,z|° t = t — dt > 0 1                ’It—b          lb с 3 узлами и  p( z) = —> 0, z e [0, t - b ]

(z ) a помощью системы уравнений [8]:

3( t — b ) ( 16 — 8 a + a ² — (12 — 8 a + a ²) (5 — a ) I     (6 — a )(2 — a )(4 — a )²

с

2 b  Г 12 — 7 a + a ² — (10 — 7 a + a ² ) _Л

+----¹--------------I = 0 о

(4 — a ) к (5 — a )(3 — a )(2 — a )(4 — a ) J j p(z)P3(z)dz = 0 о j z + b1 z a+ cz + d dz = 0

0                            0

J p(z)?3(z)zdz = 0 о J (z3 + b z2+ cz + dz dz = 0 о a                           0

t f ^b          3 2л    n     t — b ( z ³ + bz ² + cz + d ) z ²

J p ( z ) P 3 ( z ) z dz = 0 о j ²-------- _a-----1— dz = 0

a                               0

3( t — b ) (___________ 4__________

(5 — a ) к (6 — a )(2 — a )(4 — a )²

2 b  (___________2___________

(4 — a ) к (5 — a )(3 — a )(2 — a )(4 — a )

3( t — b )(3 — a ) by =--

(6 —   )

= 0 о

Выражая из первой формулы системы

(25), найдем с с учетом результата (26):

с =

- (3 - а )(2 - a ) l ( t - b )²

(5 - а )(4 - а )

+ ( t - b ) b,

(4 - а )(3 - а )

3(3 - а )(2 - а )( t - b )² (    1        2 I

----

(4 - а )        ( (5 - а )  (6 - а ) )

— 30- а (15 - ₈а + а - (1₂ - а + а ²)) — 9^ > 0 , (6 - а )²(5 - а )                                (6 - а )²(5 - а )

так как 0 <  а <  1 .

Поэтому воспользуемся формулами А.Д. Фаддеева [7, стр. 65] для трех действительных различных корней уравнения (29).

После-довательно вычисляем:

3(3 - а )(2 - а )( t - b )² ₍       )_ 3(2 - а )(3 - а )( t - b )² ₍2₇₎

(4 - а )(5 - а )(6 - а ) ^{1      1}      (5 - а )(6 - а )     ’

Получим d из первой строки системы (22) с учетом (26), (27) для найденных b 1 , с :

d = - (1 - а )

= - (1 - а )( t - b )³

( t - b ) ³ и ----— + b.

I (4 - а )   ¹

, ( t - b )² , с ( t - b ) ¹ (3 - а )   (2 - а )

—

3        3(3 - а )

(4 - а )  (6 - а )  (5 - а )(6 - а )

y — 2

„ V      ( 6 - а - (12 - 3 а )     3(3 - а )

= -(1 - а )( t - b )³1---------------- +-----------—

( (4 - а )(6 - а )    (5 - а )(6 - а )

(1 - а )(3 - а )( t - b )³ (    2        3 I

----

(6 - а )        ( (4 - а )  (5 - а ) )

(1 - а )(3 - а )( t - b )³ ( 10 - 2 а - ( 12 - 3 а ) I (6 - а )        [   (4 - а )(5 - а ) J

(1 - а )(2 - а )(3 - а )( t - b ) ³ (4 - а )(5 - а )(6 - а )

Получен ортогональный полином с учетом формул (26), (27), (28):

3,2         ,    3    3( t - b )(3 - а ) 2

P ( z ) — z + bz + cz + d — z--z +

^{3            1}                      (6 - а )

r,ф,y1,y2,y3,z 1,z2,z3,%рx2,x3 r — bc , — + d j q I ф — arccoS--I — arccoS

1  2 r у 3 — 2

< z —2

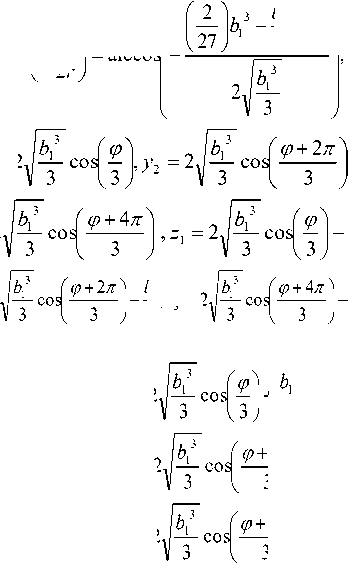
f, z 3 — ²

,(30)

b l 3 ’

+1 • (31)

^b 1

“ •

А также

— t + a - 2

+ b l 3

3 ’ x — t + a - zj x2 — t + a - z2 — t + a - 2

x ₃ — t + a - z ₃ — t + a - 2

3(2 - а )(3 - а )( t - b )²    (1 - а )(2 - а )(3 - а )( t - b )³

⁺     (5 - а )(6 - а )     z (4 - а )(5 - а )(6 - а )     '

Поскольку корни ортогонального полинома действительны [8], попарно различны, то уравнение (29) имеет три положительных корня на отрезке [0,t-b]. Кубическое уравнение (29) согласно работе [7] следует привести к каноническому уравнению заменой переменных:

bi   3             п          b,2      (2 I 3 bc , y — z+у, y + py+q— 0, p — c- у. q— l —I b1 - у-+d •

По критерию Д.К. Фаддеева [7] кубическое уравнение (29) имеет три раз-личных b² п вещественных корня если p 1 — - p — у - c >  0 •

Весовые коэффициенты C 1 , C 2 , C 3 в формуле Гаусса с найденными корнями (31) найдем с помощью классической задачи [8]:

\  1  { u (t + a - z) dz d dz   (t - b)      „   „„

и ⁽ t + a ^- z ) = 1: I --------------^— I                    ^C 1 ^{+ C} 2 ^{+ C} 3

0       z “         0 z “    (1 - а )

t -b (t + a - z) dz         t -b dz  t -b zdz u (t + a - z) — t + a - z: I -------------— (t + a) I--I

00       z                    0 z0

,     . (t - b)1-а   (t - b)2-а    „      „„

— ( t + a )--- — Cx , + C^x^ + C^x^

(1 - а)     (2 - а)      1 1     2 23 3

t - b    , _ _\2 j_               t - b j_              t - b _,_ t - b _2j_ z         x i         \ 2 c (t + a - z) dz , x? r dz            r zdz z zdz и (t + a — z) = (t + a — z) : I ---------------= (t + a) I--2(t + a) I--+ I

0        z”                     0 z”              0 z”0

2(t - b(°            t - b)2” +(t- b (°        2        22

^—(‘⁺ a )       z-²⁽ t ⁺ a г⁺z:Z ^— C i x i ⁺ C 2 x 2 ⁺ C 3 x 3 °

(1 - а )            (2 - а )    (3 - а )

НТ (1 - а )

— C + C + C

Это условие выполнено и для нашего ортогонального полинома (29).

( t + a )

(мр ( t - bf” (1 - а ) - (2 - а )

— C 1 x 1 + C ₂ x ₂ + C j x ₃

•(32)

b i    _ 3( t - b )²(3 - а ) ( (3 - а )  (2 - а ) )

3 c —    (6 - а)    ^ (6 - а)  (5 - а) J z \ 2 (t - b )1 а lit х Jt - b )2” 1(t - b f”-Г 2  „  2  „ 2

( t + a )--2( t + a )-- 1--- Cx i + Cx + Cx

(1 - а )              (2 - а )     (3 - а )      ^{1 1     2 2     3 3}

Первую строку в системе уравнений (32) умножим на x ₃ и вычтем из второй строки:

⁽ t ⁺ a - x 3 ) ⁽\. ^Ь ^   "Ут = ^C 1 ⁽ x 1 - x 3 ^{)+ C} 2 ⁽ x 2 ^- x 3 )• (33)

(1 - а )    (2 - а )

Затем вторую строку системы (32) умножим на число x ₃ и вычтем из третьей строки:

( t + a )²

( t - b Г ^{(1 - а}"

-

2( t + a )

( t - b ) ^{2 - а} (2 - а )

, ( t - b ‘ (3 - а )

— ( t + a ) X j

⁽ t ^- b ^{) 1- а} ₊ x j t - b r ^ (1 - а )     (2 - а )

= C 1 ^x 1 ^{( X} 1

^- x 3 ⁾⁺ C 2 x 2 ⁽ x 2 ^- x 3 ) °⁽ t + a ⁾⁽ t + a ^- x 3 ) ⁽    )

(1 - а )

-^{( 2}( t + a ) ^{- x} 3 /    ’    +^   )    = C 1 ^x 1 ^{( X} 1 ^- x 3 ⁾⁺ C 2 x 2 ⁽ x 2 ^{- x} 3 ) .⁽³⁴⁾

(2 - a )    (3 - a )

Выражение (33) умножим на x ₂ и вычтем из полученного (34).

( t + a ⁾⁽ t + a ^- x 3 ) ⁽ t - ^{b )}     I 2l t + a ) ^- x 3 ^{) (} t - b )   + ^{( t} - b )   ^-

(1 - а )                  (2 - а )    (3 - а )

- ( t + a - x^ ) % 2

MT ^{(1 -} а )

+ x

² (2 - а )

= C 1 ^x 1 ^{( x} 1

^- x 3 ^)- C 1 x 2 ^{( x} 1

^- x 3 ) = C 1 ⁽ x 1 ^- x 2 ⁾⁽ x 1 ^- x 3 ) =

⁽ t - b ^а                          t - b '2" +⁽ t - b ) ' "

= ⁽ t ⁺ a - x 2 ⁾⁽ t ⁺ a - x ³⁾— -⁽2⁽ t ⁺ a ) - x ³ - x ₂ ) -(2—)- ⁺ -(3—)-

Из последнего уравнения выразим С :

(или в формуле (19) с параметром a =0) используется одни раз. Как и используется один раз формула (18) с равномерным шагом для вычисления первого интеграла в (17).

Замечание 1. Для дробной производной на интервале (0,1) в упрощенном алгоритме в Утверждении 1 нужно выбрать функцию и вес: u ( t - z ) ^ u ' ( t - z ) a = 0, р ( z ) = 1/ z^a , a e (0,1) •

А на интервале (1,2) нужно выбрать функцию u ( x ) c другим весом:

u ( t - z ) ^ u " ( t - z ), a = 0, p ( z ) = 1/ z ^а - ¹, a e (1,2) .

И в этом случае две формулы (20), (21) Утверждения 1 останутся верными, если в них формально заменить a-->a-1 и заменить весовую функцию.

Пользуясь формулами (10), (12) и соответствующим численным алгоритмом (18), (20), (21), составим таблицу для численного значения дробной производной и аналитического значения производной с помощью ряда (16) для функции f ( t ) = sin( t ), t = 1, а e (0,2) .

Таблица 1. Производная Герасимова-Капуто для функции u ( t ) = sin( t ), t = п /2, а e (0,2)

C 1 =

⁽ x 1 - x 2 X x 1

-

^x 3 )

( t + a - x ₂)( t + a - x ₃)

( t - b ) ^{1 -а}

(1 - а )

-

- ( 2( t + a ) - x - x ₂ ) ^{( t}  b )   + ⁽ t  b )   ] •  (35)

^{V            3    27} (2 - а )     (3 - а ) I ^{V 7}

С учетом (35) из формулы (33) найдем C ₂ :

С ( x - x ,)        1     (             ( t - b ) ^{1 а}   ( t - b ) ^{2 a >}

= -            +         I ( t + a - x ₃)-

( x - x s )   ( x ₂ - x ₃ ) ^             (1 - а )    (2 - а ) _;

1            f.                          .( t - b ) ^{1 - а}

■7------V-------J ⁽ t ⁺ a ^{- x} 2⁾⁽ t ⁺ a ^{- x} 3),, \--(²⁽ t ⁺ a ) ^{- x} 3

( x 1 - x ₂ \ x 2 - x 3 ) I                            (1 - a )

_x > ( t ^- b У- ^{а 2}   (2 - а )

l ( t ^{- b} ) ³ - " ) (3 - а ) J

+ 7--------г¹ ( t + a - x-, )

( x 2 - x 3 Ж        ^3j

( t - b ) ^{1 -} "    ( t - b )

—

(1 - а )    (2 - а ) J

( t + a - x 3 )( x 1 - 1 - a ) ( t - b )     ( 2( t + a ) - x । - x 3 it t - b )              ( t - b )

( x - x )( x - x )    (1 - а )    ( x - x)( x - x ) (2 - а )    ( x - x \ X - ^х з ) (3 - а )

=         1 ( x 1 - x 21 x 2 - x 3 )

2         v        J t - b ) " ° hr \        \( t - bV ( t - b )3- а ( t + a x 3X x 1 t a ) ^^ +( 2( t + a ) x 1 x 3 )^^ ■ ^^

Из системы (32) выразим С ₃:

с 3         , - с 2 - с 1              (37)

(1 - а )

Результаты формул (37), (36), (35), (31), (30), (29), (28), (27) совпадают с формулами (20), (21) и Утверждение 1 доказано. Отметим также, что в упрощенном алгоритме квадратурная формула Гаусса (20), (21) для вычисления второго интеграла в формуле (17)

a	( D 0 + , t sin( t ) ) ( t = п / 2 )	( D" t s in( t ) ) \  0+, t      \ n>num ( t = п / 2 )	a ( d "+ , t ) ( t = п /2 )
10-14	0.9999999999 99995	0.99999999999 9994	1.7763568 3E-015
10-8	0.9999999952 79993	0.99999999527 9997	-4.1078E-015
0.1	0.9470275154 07809	0.94702751540 7803	5.9952043 32E-015
0.4	0.7184255171 19136	0.71842551711 9135	1.4432899 32E-015
0.5	0.6197920300 73509	0.61979203007 3510	-1.4432E-015
0.6	0.5109932063 84873	0.51099320638 4873	2.2204460 49E-016
0.9	0.1357686082 62797	0.13576860826 2797	2.4980018 05E-016
1-10-8	1.3707621751 9046E-008	1.37076218024 3091E-008	-5.0526E-017
1-10-14	1.3871023850 6829E-014	1.37579260713 4274E-014	1.1309777 93E-016
1+10 14	-1.371991E-014	-1.3100631E-014	-6.1927E-016
1+10-8	-1.370762E-008	-1.3707621E-008	-3.7398E-016
1.1	-0.13758466 5279301	-0.13758466 5279305	3.9690473 13E-015
1.4	-0.53501308 1857711	-0.535013081 857709	-2.2204E-015
1.5	-0.65277766 5939620	-0.65277766 5939619	-8.8817E-016
1.6	-0.75817951 8757917	-0.758179518 757916	-6.6613E-016
1.9	-0.97151962 2786878	-0.971519622 786876	-2.3314E-015
2-10-8	-0.99999999 8353808	-0.999999998 353809	-  2.220E- 016
2-10-14	-0.99999999 9999998	-0.999999999 999998	1.1102230 2E-016

Аналогичную таблицу для численного и аналитического значений производной с помощью ряда (15) составим для функции f ( t ) = cos( t ), t = 1, a e (0,2) . Первая часть и вторая часть каждой таблицы на интервалах (0,1) и (1,2) находится разными алгоритмами и программами с особенностями, описанными в Замечании 1.

Из табл. 1 для функции

u ( t ) = sin( t ), t = n/2, a e [ 0,2lsin| — I ^ 1 - 0

I 2 J ^a —+ 0

(П I   , , л • I П I            ~ cos| — I   ^ + 0,— sin| — I   ^ — 1 + 0,

I 2 J a — 1 — 0           I 2 J a — 2 — 0

что соответствует производным u ( t ) = sin( t ) .

Из табл. 2 для функции

Таблица 2. Производная Герасимова–Капуто для функции u ( t ) = cos( t ), t = n /2, ae (0,2)

a	( D 0 a + , t cos( t ) ) ( t = П / 2 )	( Da 1 cos( t ) ) u + , 1       п/тт ( t = П / 2 )	a ( d 0 + , tcos(t ( t = П /2 )
10-14	-1.36710160 44627E-014	-1.310063169 057677E-014	-5.70384E-016
10-8	-1.37076214 99648E-008	-1.370762118 117236E-008	-3.18475E-016
0.1	-0.13758466 5279301	-0.137584665 279305	4.218847493 57E-015
0.4	-0.53501308 1857711	-0.535013081 857709	-1.77635E-015
0.5	-0.65277766 5939620	-0.652777665 939619	-8.88178E-016
0.6	-0.75817951 8757917	-0.758179518 757916	-1.22124E-015
0.9	-0.97151962 2786878	-0.971519622 786876	-2.22044E-015
110-8	-0.99999999 8353808	-0.999999998 353809	2.220446049 25E-016
1-10 14	-0.99999999 9999998	-0.99999999 9999998	1.110223024 625E-016
1+ 10-14	-0.99999999 9999998	-0.9999999 99999998	1.110223024 625E-016
1 +10-8	-0.99999999 95279994	-0.999999995 279997	3.885780586 188E-015
1.1	-0.94702751 5407809	-0.947027515 407803	-5.99520E-015
1.4	-0.71842551 7119136	-0.718425517 119135	-1.33226E-015
1.5	-0.61979203 0073509	-0.619792030 073510	1.443289932 012E-015
1.6	-0.51099320 6384873	-0.510993206 384873	-5.55111E-016
1.9	-0.13576860 8262798	-0.135768608 262797	-3.33066E-016
210-8	-1.37076217 51904E-008	-1.370762165 002316E-008	-1.01881E-016
2 10-14	-1.38710238 50682E-014	-1.375792607 134274E-014	-1.13097E-016

Таблицы 1 и 2 получены при следующих параметрах n=10000,nh=b (n-число интервалов для отрезка в первом интеграле в (17)), l=45, 45h=t-b –длина правого отрезка в квадратуре Гаусса.

Первый столбец – порядок производной a , второй столбец - аналитическое значение производной Герасимова по формулам (15), (16), третий – численное значение производной по алгоритму (18), (20), (21). Четвертый столбец – разность между аналитическим и численным значениями дробной производной.

u ( t ) = cos( t ), t = n /2, a e [ 0,2 ], cos| ^П | = —0 — a = +0

• • I ^П I      1   ,        1         I ^П I      Л .        Л Л

• — sin| — I = —1 —— a = 1,—cos| — I = —0 —— a = 2 — 0 ,

• 12 J               \ 2 J

что соответствует производным u ( t ) = cos( t ) .

Основные полученные результаты:

• 1)    Впервые получены модифицированные формулы (10), (12), (13) Герасимова– Капуто.

• 2)    С учетом модифицированных формул (10), (12) получен численный алгоритм (18), (20), (21) и доказана корректность алгоритма – Утверждение 1 .

• 3)    Результаты алгоритма (18)–(21) сравнены с аналитическими формулами (15), (16), невязка вычислений не превышает 10^-15 .

• 4)    Формулы (20), (21) Утверждения 1 остаются верными при формальной замене в них α на интервале (0,1) на α-1 на интервале (1,2) .