Модифицированная формула Ньютона - касательных парабол на числовой оси

Эта работа © 2023 Волосова Н.К., Волосов К.А., Волосова А.К., Карлов М.И., Пастухов Д.Ф., Пастухов Ю.Ф. под лицензией CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите

Итерационная формула касательных Ньютона для численного решения нелинейных уравнений содержится во всех учебниках по численным методам [1], [2]. Также эта формула используется профессором В.М. Тихомировым для поиска точек экстремума в конечномерных задачах на безусловный экстремум [3]. Следовательно, алгоритм может косвенно использоваться и в сложных задачах на экстремум, например в задаче Л.С. Понтрягина [4], [5]. В случае кратного корня нелинейного уравнения порядок скорости сходимости невязки для итерационной формулы Ньютона падает со второго до первого [1], [2].

Авторы работы [1] предложили модифицированную формулу касательных Ньютона.

В данной работе также получена модифицированная формула Ньютона касательных парабол. Аналитическая формула (11) затем обобщена для аргумента z на всю числовую прямую и имеет вид ряда (18) с одиннадцатью слагаемыми. Показано, что новая формула (18) имеет те же свойства, что и аналитическая формула касательных парабол (11), но требует меньшее число итераций, чем форму- ла Ньютона и модифицированная формула Ньютона для поиска корня кратности m=1 с заданной точностью. Для кратности корня m≥2 нами предложен алгоритм (21), (22) который, как и модифицированная формула Ньютона (23), находит корень с двойной точностью за одну итерацию. Алгоритм (21), (22) работает со вторым порядком скорости в более широкой области принадлежности корня и начальной итерации, чем простая модифицированная формула Ньютона (23) для кратного корня.

Постановка задачи

Рассмотрим итерационную формулу касательных Ньютона (2) [1] для отыскания корней функции одной действительной переменной (1):

f (x) = 0, x e R, f (x) e R ;(1)

xn+1 = xn - -yxrk, n = 0’1,2’- .

^{f (} x n )

Начальная итерация x ₀ :

x 0 e [ a , b ], f ( a ) f ( b ) <  0, f ( x ) e C 1 [ a , b ]

принадлежит отрезку с изолированным кор.*

нем x . По определению корня всегда f ( x ) = 0 .

Кроме того, производные порядка m -1 включительно в точке корня х . могут быть равны нулю: f ⁽ k ⁾ ( х) = 0, к = 0, m - 1 , тогда функция

Формулу (6) перепишем в эквивалентном виде (8):

f ( х ) представима в виде

*\                      л*е

f ^{( m - 1)} I х I                    f ^{( m} ) I х I

*                                     *

f ( х ) = f I х I + ... +           ( х - х ) ^{m - 1} +---- У ( х - х ) ^m +

V )         ( m - 1)!                   m !

к,    (mm + к ) / * Л       *

+ 1        |х|(х - х) m+k mm + к)! v )

*     к

= ( х - х)m Е к=0

у ( m + к ) ( m + к )!

**

х | ( х - х ) ^к =

*      к     /*( m + к ) * *\       *              *

= ^{( х - х} ) ^m Ет— ^1 ^х I ^{( х - х} ) ^к = ^{( х - х} ) ^m ^ ^{( х ),} к = 0 ( m + к )! V )

к    (mm + к ) А\      *        *      /■( m )                    *

^ ( х ) = Е / ,J х I ( х - х ) ^к , ^ ( х ) = —I х к 0, f^{( m} ) ( х ) * 0 .

к = 0 ⁽ m ^{+ к )!} V )                   m ! V )

*

Тогда про корень х говорят, что он имеет кратность m . При выводе формулы (2) в последовательности точек касания ( х_п , f ( х_п ) ) графика функции ( х , f ( х ) ) предполагалось,

^х 1, n + 1 = ^х 1, n ⁺

^х 2, n + 1     ^х 2, n

- fn + V(fn ) - 2 fnfn

—

fl fn +7(fn ) - 2 fnfn

V

f n

. (8) , О 0

)

В формулах (8) из правой и левой части *

вычтем значение корня х , обозначим разность 5 1n = х _1; n - х , 5 ₂ , n = х ₂ , n - х , формулы (8) перейдут в формулы невязок:

5 1, n + 1 = 5 1, n +

- ^fn ⁺V⁽ f n ) - ^{2 f}n^fn

<

5 2, n + 1 = 5 ₂, n +

- fn-^fn ) - ^{2 f}n^fn

. (9)

fn

, f n * 0

что касательное множество точек - прямая

У (х) = fn + (х - хп) fn  имеет два очевидных условия согласования: у(хп) = fn, у (хп) = f n.

Идея данной работы заключается в использовании касательного множества точек с тремя условиями согласования (метод "касательных парабол"):

у ( х ) = f n + ( х - х „ ) f n ' + ^{( х -} х ^{)2 f n} ..   (4)

У ^{( х} „ ) = fn , У '^{( х} ” ) = f n , У ''^{( х} „ ) = fn .

Следующую точку итерации найдем из условия пересечения действительной оси и касательной параболы (4), обозначим

^А n = ^хп + 1 ^{- х}п ,

У ⁽ х „ + 1 ) = ⁰ » ⁰ = f n ⁺ A „^f„ ⁺—^ о «А n ² f „ '+ 2 A „ f „ + 2 f , = 0 .       (5)

Последнее уравнение имеет два корня:

A

n

- f n ±У ( f n ) ² - 2 f_nf; fn'

f* 0 .

Определение 1 [1]. Говорят, что беско- нечно малая числовая последовательность

5„  >  0 сходится к нулю с порядком скорости

” ^к р, если существует предел

0 <  lim ' ” ⁺¹' = C < +к .

”  ■

Если в формуле (6) выражение ( f n ) 2 - 2 f n f ” ' <  0 , то ^А ” будет комплексным.

В последних формулах (9) вынесем модуль | f | из корня, получим

- ^fn ⁺| ^fn | ¹ - ^{2 f}n^fn ^{/ (} fn) _

• 51,    n+1 = 51, n +                 7"

fn

= 5ln - 4 f1 - J1 - 2 ff '/(f'n )21 fl* 0, f> 0 , (10 a) 1,n                          nJ n     n          nn f fl V fn    fn         fn fn fn

• ⁵ 2,    n + 1 = ⁵ 2, n ⁺------- _f--------------

• fn

  =5n-ffh - ^-4444 1,14*0,f<0. (10b)

2, ”                       ” П”     n            ”

^f n ^V                          J

Таким образом, две формулы (10a) с положительным значением производной функции fn> 0 и (10b) с отрицательным зна чением производной fn< 0 объединим в одну итерационную формулу (11) без индекса 1 или 2, считая при преобразованиях формулы (11) для простоты f > 0 .

f^A1

5n+1 = 5n -yl1 - г - 2 fnfn /(fn ) I, \fn\ * 0 . (11) f n V

Обозначим в формуле (1) m кратность х ^* корня, тогда по определению кратности можно записать

/     * Am*

f ( х ) = | х - х | ^ ( х ), ^ ( х ) * 0, m >  1 .

Найдем первую и вторую производные от функции f ( х ) :

/    .4 m - 1         f * \m           .

I I                                         I I f (x) = ml x-x I   p(x)+1 x-x I p(x),p(x) *0

(    . \m ^{- 2}            (    . \m ^{- 1}

f ( x ) = m ( m - 1) l x - x I    p ( x ) + 2 m I x - x I

* m^m

II p ( x ) +l x - x I

(.

p ( x )

То есть, порядок степени δ n в правой части последней формулы – два либо больше.

Во втором случае для кратности m =2

аналогично из (14) получим

Необходимо переписать формулы (11) в итерационном виде:

d n + 1

^ d n 1 - n ^M

v

,          2              1

m ( 1 + 71" - 2( m - 1) / m )₂

m = 2

*

^{f (} x n ) = fn =l x n ^- x I P ⁽ x n ) = ^ n P n ,       ⁽¹³⁾

= d n

"1- i        2          .

v 2 ( 1 + 71 - 2(2 - 1)/2]

= d n (1 - 1) = 0 + o ( d n ) = o ( d n ) .

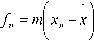
p ^{( x}„ ) ^{+ f x} n ^{- x} I p ^{( x}„ ) = m ^d m ^{- l} p n ⁺ S'p n ^{,  (13} а )

/     л m -2            /     *\m-1         /     *\m fn' = m(m-IR - x I   p( xn ) + 2 mlxn - x I p( xn ) + | xn - x I p'( xn ) =

= m ( m - 1) d n^{m - 2} p n + 2 m d m ^{- 1} p „ + d m p' n .      (13 b )

То есть, порядок степени δ n в правой части последней формулы – два и более. Следовательно, по определению 1 имеем, что порядок скорости сходимости итерации в формуле (11) –

Лемма 1. Формула (11) корректна для кратности корня m =1 или m =2, при этом порядок скорости сходимости d _n выше первого (второй или выше).

Доказательство *                          *

В пределе x_n ^ x о d _n = x_n - x ^ 0 . n ^»                n ^»

Тогда в формулах (13), (13 a ), (13 b ), выделяя главное предельное слагаемое, получим

не менее двух для кратности корня уравнения (1) m =1 или m =2. Подкоренное значение в (14) неотрицательно (условие корректности формулы (11) для действительных значений δ n ), если

1 - 2( m - 1)/ m >  0 о m - 2( m - 1) = 2 - m >  0 о m <  2 о m = { 1,2 } .

f n = d m p n , f'_n « m d m p , f n . m ( m - 1) d n^m p .

А формула (11) получит предельный вид

d n + i = d n - f ^ ^f 1 - 7 1 - 2 f n f n / ( f n ) ² 1« f n ^{v                      2}

» d n - -m ^ m pr- f l -J I - 2 8 m p_n m ( m - 1 ^ - p /(m d m p ) 2 Ъ ^{m ( m - 1) d} n p n v                                       2

d n + 1 ^ d n --f- ( 1 - 7 1 - 2( m - 1)/ m ) .

ⁿ        ( m - 1)

Преобразуем последнюю формулу

Поэтому важно получить другую формулу аналогичную (11) при кратности корня m >2 на всей числовой прямой.

Лемма 1 доказана.

Производные функции f(x) из формул (13), (13 a ), (13 b ) подставим в формулу (11), получим (15)

d n + 1

I

v

d n + 1 ^ d n - -^ n- ( 1 - J 1 - 2( m - 1)/ m ) = n        ( m - 1)

d n + 1

= ^d n ¹

—

2( m - 1)/ m

( m - 1) ( 1 + 71 - 2( m - 1) / m ) ₂

= ^d n ¹

—

v

2            ¹

m ( 1 + 71" - 2( m - 1) / m ) ₂

В первом случае для кратности m =1 из

формулы (14) получим

d n + 1

f

^ dn 1 - n ^^

v

,          2              I m (1 + 71"_ 2( m -1) / m) 2

= d n

1 -

v

( 1 + 71 - 2(1 - 1)/1 ) _;

= d n (1 - 1) = 0 + o ( d n ) = o ( d n ) .

. I           m d m ^{- 1} p n + d m p n           I

= d -                                  • v m(m - 1)Sm-2pn + 2mdm-1 p n + dmp n J

8P^d m < m —Pp^^

m d m p + d m p n ) ²          2

= d n - d n

₁₊ dp mp n

v

1 no p n о 2 p n m -1 + 2dn — + dn  — pn      mpn J

•

f

^f f m - 1 1   -pPv „2 p n

I I         1 ^{+ 2         + d} n

12   m 2   mpn     m pn f1 + dn ^n- J v     mpn 2

Заметим, что формула (15) является точной.

Введем упрощающие преобразования обозначения:

a = —-, b = —n , p _n * 0, l a i <» ,I b l <» , p n       p n

Z = 2 f n f n / ( f n ) ², a = 1P , B = f n- . f_n

С учетом новых обозначений перепишем формулу (15):

S " + , = S " — B ( 1 — A ) = S " — B ( 1 — 7—7 ) , B = S "

1 + 4 a

m

,

m — 1 + 28 " a + 8 „² b k                m J

m — 1

B = S "

1 + 8

m

A

m — 1 + 28"a + 8„2 b k               m J

1 + a S "

2 a ^[ 1 + ⁸ k     2 a

z = 2

m

+ "    + 8 " ² Л 1

. m .2 m ^J , a = 1      •  (16)

a 1

1 + S - I m J

1л            bSn

= —(1 + a S" ) 1-- "

2 a        " 4     2 a

¹ I 1 , S’ I ^b 1 , 2" = —¹ 1 + S„ | a --I+ 8

" a      k "  a J

—

b 2 8 2

4 a ²

—

b 38" 3

---" + o¹ 8 a ³

b   b ² 1 _s3i

2 47 J^{+ 8}

—

—

b ³

8 a ³

—

b 1+ o

4 a I

8 ) •

J

Учитывая Лемму 1, уточним порядок скорости для невязки S " в формулах (15), (16).

Лемма 2. Формула (16) для кратности корня m =1 имеет третий порядок скорости сходимости невязки к нулю 8 ^ 0 • ^да

Доказательство. В случае m=1 дробь z в формуле (16) имеет вид, с использованием разложения в ряд Тейлора известной формулы р- = 1 — x — x2 + o (x2), | x < 1

Перепишем формулу (16) при m=1 с учетом найденных выражений A = J1 — z, B

8 " + 1 = 8 " — B ( 1 — A ) =

= 8 —

1 1 J b 1 ,₂ - ^{1+ 8} " | a ^— -I + 8 k "  a J

2 a

к

к

к

b b ² L₃ ----7 I + 8„

"4 a ² J "

—

к

ь ³    ь ² 1 ^3 i

—- —1+ o [8 ) • 8 a³ 4 a J       " JI

z = 2

m — ¹ 1+ 2 4 a + s

m

m a 1

1 ^{+ 8} " - I m J

2 b

n m2

= " s„           ⁸

" 1 + 2 a S " + a " 8²

= 4 a S "

" ^{— a}

" S, 2 — 4 a 8 2 + o ( s 2 )) =

= 4 a S " | 1 + S "

Применим формулу Тейлора для квад-

ратного корня <1 — x = 1

x x ²

2   8   16

z ³ — + o l

x + o ( x ³) :

¹ ( z ³ )=

= 1 — 2 a S " I 1 + S ,

—

— 2 a ²S„ ² 1 1 + 2S " | ^b — 2 a 11 — 4 a³ S_n ³ + o (s _n ¹) = k        k " a       J J

= 1 — 2 aS" + S" ³ ( — b + 4 a ² — 2 a ² ) +

+ S" ( " ab + 10 a ³ — 2 ab + 8 a ³ — 4 a ³ ) + o (s„ ¹ ) = = 1 — 2 a S " + S " ( — b + 2 a ² ) + 14 a 3 8 3 + o ( s " ) 1 — A = 2 a S " + S " ( b — 2 a ² ) — 14 a³ 8 " + o ( s ³) =

= 2 aS„ 11 + S„ I — — al — 7 a 2S„2 + oi fl \                      fl I                                                                  fl k       k" a J

Далее преобразуем дробь B для кратности корня m =1:

• 2 aS_n 1 1 + S_n I — — a I — 7 a2S_n ² + o l

\                                                                                              fl k        k" a J

= ⁸ " ^—

+ S"²

_s J b b 1

8 " 1 1 + 8 " | a — -—+ 7— a I +

¹ b b²

— —

2  4 a ²

к

—S3

fl

b

2 a 2 a

—

7 a ² —

^{— 8} a ^{2 —} 2a" I + o ^{( s} 3) •

Согласно определению 1,

_r K J b lim       =

^{8 ,o} I⁸ I"

" ^M    "|

— 8 a ² — 71

2 a ²

= С < да , p = 3 .

А невязка итерационной формулы (15) при m =1 имеет третий порядок скорости. Лемма 2 доказана.

Лемма 3. Формула (15) для кратности корня m =2 имеет второй порядок скорости стремления невязки к нулю S_n ^ 0 • "  ^да

Доказательство. В случае m =2 дробь z в формуле (16) имеет вид, с использованием разложения в ряд Тейлора известной формулы,

— = 1 - x - x ² - x ³ + o ( x ³) | x | < 1; 1 + x

m — 1

о k m z = 2----

+ 2 8 + 8„" b m     m2

■■■ m J

= " ^[ " ^{+ S} " a ^{+ 8 2} 4 ¹   1 + 2 8 " a + S"³ b

[1 + "aI"        1 + S"a + S2 a k " J                        4

1 + 2 8„ a + 8„² b || 1 — 8_n a — 8_n ² — rl       n 2/1        n       . 4

—

Разложим в ряд Тейлора функцию

I c2 2    ⁸ a 1

— | 8 ² a ² + —— + o l

I                2

Il 2       £21 Ь 5 a ²    _21    „3|

= ^| 1 + 8 a + 8 ¹---- 2 a  ¹ + 8 \

I '       ^- 1 2      4              I ^-

I

| ^{— 8} - a ⁺ o ^{( 8} - ) =

J

3 a ³ ab 5 ₃Y ------a | + o

2    2   2 JJ

5!

x ³

--+

+

= 1 + 8 - a + 8- ²

f Ь 13 a ² 1 c

1 2^—“4"   ⁸

+

'& ) ,1 — A = 1 — ^/— 8 - a + o ( 8 - ) .

Далее преобразуем дробь B для кратности корня m =2:

B = ⁸ -

1+^

л

1 + 28na + 8-2 b l              2 J

41+a8 I n l 2 J

1 + 2 8_na + 8- ² b

+

9!

= 8 -

1 — 2 8 - a — 8 - b —|

| — f 2 8 „ a + 8 -² Ь

B = 8 „ 1 1 — ^ a + 8;

^- 1          2          n

'„^{11 — 4} a ^{2 —} I^— a ^{21+ o ( 8} Y) J =

2 xx

=   2 T

—

429 x ⁸   715 x

3 x

—

= 8 -

—

— 8 ² + o 8 2 ) . nn

Перепишем формулу (16) при m =2 учетом выражений A = 4 1 — z , B

с

⁸ - + 1 = ⁸ - ^{— B ( 1 —} A ) = ⁸ - ^— f ⁸ - ^{— 8} + ⁺ o

♦

• ⁽ 1 ^—\^{— 8} - a + o ( ⁸ - ) ) = —⁸ - ² + o ⁽⁸ - ) .

Согласно определению 1,

18-+1|    3 a lim---- = — = С < да, p = 2.

8 - 4018 I²     2            ^F

- 4X | — n\

А невязка итерационной формулы (15) при m =2 имеет второй порядок скорости. Лемма 3 доказана.

Замечание 1. Согласно Лемме 1 итерационная формула (11) корректна только для кратности корня m =1, 2. Но даже в этом случае из-за наличия арифметического квадратного корня формула (11) численно ограничена, так как при отрицательном подкоренном значении программа блокируется функцией SQRT.

Поэтому в данной работе мы предложили новую идею для вычисления формулы (11) при любой кратности корня и даже при отрицательном подкоренном значении в (11).

¹ If ¹Y ³ Y ⁵1 4

II II II                   I x

---TV---TV---'-- +

7!

8!

+

11!

5 x ⁴    7 x ⁵

—

4!

6!

10!

+ o ( x ¹¹ ) =

21 x ⁶    33 x ⁷

128  256  1

2431 x ¹⁰   4199 x ¹

—

32768  65536  262144   524288

- + o l

+

+

+

+

• ( x ¹¹ ) .      (17)

В зависимости от кратности корня переменная z принимает значения:

m' 1+ 2    ' + 8,

2 ll m

z = >

m a I

1 + 8-     I mJ

m — 1 1

2----- I <  2, m >  2

I m J

. 2 Ь ¹

n m2 J

--------= 4 a 8 _- + o ( 8 . ), m = 1

.

Формула (11) с учетом формулы (17) примет вид ряда

f f z z ² z ³    5 z ⁴    7 z⁵    21 z ⁶    33 z⁷

8     = 8 I ¹¹¹¹¹¹+

^{- + 1     -} f I 2   8   16   128   256   1024   2048

429z8

+---1+

2431 z ¹⁰    4199 z ¹¹

1+ o ।

262144   524288

Q

x" ^{+ 1} = x^- —

z ³    5 z ⁴    7 z ⁵    21 z ⁶    33 z ⁷

ffz  z2_

—7 I — +---1---1---1---1---1+ fl 2   8   16  128  256  10242048

n

429 z⁸    715 z ⁹    2431 z¹⁰    4199 z ¹¹    (

+-------+-------+--------+--------+ o ( z  ) |(18)

32768  65536   262144   524288     ^v A

Так как

z = ² f - f - '/ l f - ) ²    4

2( m — 1)

m

> 0, m > 2; 4 4 8- f 8 40 m — 1

формулу (18) для малых 8 n ^ 0 можно при-

близить формулой

429 z8   715 z9   2431 z10   4199 z11)

+---1---1---1--

32768  65536  262144   524288

S +1 = S 1

—

V

1 f z z2 z3   5z4   7z5   21 z633

1+ m — 11 2   8   16  128  256  10242048

С учетом формул (18 b ), (19) получим формулу (20):

429 z ⁸   715 z ⁹   2431 z ¹⁰   4199 z ¹¹

I---1---1---1--

32768  65536  262144   524288

+ o ( z ¹¹ ) I I . (18 а )

S + 1 J s _n

—

В (18 a ) сумма 5 n+i монотонно убывает с каждым новым слагаемым. Формулу (18 a )

1 f z   z2   z3   5 z4   7 z5   21 z6

(m — 1) V 2   8   16  128  256  10242048

429 z8   715 z9   2431 z10   4199 z11

++++q I.(20)

32768  65536   262144   524288 ’ I '

перепишем в эквивалентном виде:

S n _{+ 1}   ,      1 f z z ² z³    5 z ⁴    7 z⁵    21 z ⁶    33 z⁷

— 1 1111111

S       m — 1 V 2   8   16  128  256  1024  2048

429 z ⁸

+--

715 z ⁹

+--

2431 z ¹⁰   4199 z ¹¹

+

262144   524288

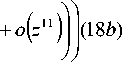
Теорема 1. Существует единственное значение параметра q в формуле (19), для которого Y ( q ) — 0 , что равносильно в формуле (20) д _п + 1 — O ( s ) p >  2.

Доказательство. По известной теореме

Обозначим

Y 1

— 1—

1 I z   z ²    z³    5 z ⁴   7 z⁵    21 z ⁶   33 z⁷

------------------------------------------------------1--1---1---1---1---1---1-- ( m — 1) V 2   8   16  128  256  1024  2048

429 z ⁸   715 z ⁹

+--- 1--

32768  65536

2431 z ¹⁰

+--

+ О ( z ¹⁰),

из математического анализа непрерывная на отрезке функция, в нашем случае линейная по переменной q (19), принимающая противоположные знаки на концах отрезка имеет не менее одного корня на отрезке. В силу линейности функции (19) такой корень единственный.

Введем обозначения

Y 2 = 1 —

z z ² z ³    5 z ⁴    7 z ⁵    21 z ⁶    33 z ⁷

A ^ˆ

z z ² z ³    5 z ⁴    7 z ⁵    21 z ⁶    33 z ⁷

— I--1— I--1--1--1--+

------------------------------------1--1---1---1---1---1---1---+ ( m — 1) V 2   8   16  128  256  1024  2048

2   8   16  128  256  1024  2048

429 z ⁸

+

429 z ⁸

+--

715 z ⁹

⁺ 65536

2431 z ¹⁰

+--

4199 z ¹¹

+--

+ o ( z ¹¹) .

715 z⁹    2431 z¹⁰   -   4199 z ¹¹       2( m — 1)

+---1--, B —--------- , z —---------

65536  262144     524288         m

Перепишем формулу (19) в виде

Из формулы (18 b ) видно, что при некотором максимальном числе членов ряда (численно установлено: оно равно десяти) знаки S _{n + 1}, S _n еще совпадают Y >  0 , а при числе чле

Y — 1 —

( m — 1)

( A + В ■ q )

нов ряда равном одиннадцати знаки S n _{+ 1}, S _n противоположны Y 2 <  0 .

Действительно, программа дает значения Y 1 , Y 2 для функции f(x)=(x-2)^m

Y — 0.33428534 9277 , Y — -5.5254551 174E -002, q = 0.85815432 2291434 < 1,m — 30

I    /III

Y — (1 — q ) l 1--- I + q l 1

m — 1

—

Л

A + В m — 1

— (1 — q ) y + qY^ >  0 .

Y — 0.11311156 1929290 , Y₂ — -0.3779228 24952878, q = 0.23035364 7221112 <  1, m — 20

Y — 2.37936767 3E - 002 , Y₂ — -7.1020265 95E - 002, q = 0.25095124 2652344 <  1, m — 3 .

Из последней формулы видно, что числовой вектор Y(q) пробегает весь отрезок [Y 1 Y 2 ] пока параметр q пробегает единичный отрезок [0,1], как показано в главе "Выпуклый анализ" авторами [3], Y(0)=Y 1 , Y(1)=Y₂. Вычислим параметр q из условия Y(q)=0: ˆ      ˆˆ

Y — 1---, Y2 — 1— A—q, Y > 0, Y2 < 0 , m — 1        m — 1

Значения Y ₁, Y 2 зависят от кратности корня m. Из формулы (18 b ) видно, что всегда найдется конечное число членов ряда, для которого Y >  0, Y 2 <  0 , так как каждое новое сла

Y — 1--— ( A + В ■ q ) — 0,

( m — 1)^V        ’

гаемое ряда уменьшает его сумму. Рассмот-

ˆ

Y — Bq- — 0 » q — ^{Y (} m ^{— 1}} ,       (21)

m — 1            В

(1 — q ) Y + qY 2 — 0 О q — -BY— — -Y — <  1 (21 а )

^Y 1 ^{— Y} 2    ^Y 1 ^{+ Y} 2

рим ряд с конечным числом слагаемых и с

То есть, Y ( q ) — 0 . Из формулы (20) имеем

параметром q:

Y — 1 —

( m — 1)

z z ² z ³    5 z ⁴    7 z ⁵    21 z ⁶    33 z ⁷

- + — + — +--+--+---+---+

2   8   16  128  256  1024  2048

' / — Y ( q ) — 0 о 8 _n + 1 — O S p ) p >  2 . ^Ъ

Теорема 1 доказана.

Итак, мы имеем итерационную формулу (22):

„+1 л fJ z  z2   z3   5z4   7z5   21 z633

Xn+1 = xn - ini - +--+ — +---+---+----++ fl 2   8   16  128  256  10242048

n

429 z8   715 z9   2431 z10   4199 z11

+111--- q I . (22)

32768  65536  262144   524288

z = 2 f_nf"/ ( f n ) 2 , где параметр q определяется формулой (21) c переменной z = 2( m - 1)/ m , m – кратность корня. Кратность корня легко определяется формулой

1 m =------...

1 — f n f n / ( f n )

Программа для примера 2 дает значение m = 30.

Приведем также модифицированную формулу Ньютона, полученную школой профессора Н.С. Бахвалова [1]:

x n + 1

= x n

^{f (} x n ) ^{f (} x n ) ^f'( x n ) ^f'⁽ x n ^{)- f (} x n ) ^f" ( .x n )

, n = 0,1,2,... . (23)

Замечание 2. Вычислительный эксперимент показывает при кратности корня m=1, что все слагаемые в формуле (18) важны. Например, если число слагаемых в (18) равно 3, то итерационная формула (18) для функции f (x) = sinx—x 2/2 = 0, x = 0, x2 = 1.40441482 409243, m = m2 = 1

с начальной точкой итерации x⁰ = 5 теряет ближний корень x ₂ = 1.40441482 409243 и находит второй корень. Если число слагаемых равно 4, то формула Ньютона (2), модифицированная формула Ньютона (23) и формула парабол (18) дают ближайший корень с двойной точностью за 7 итераций:

x (18) =  1.40441482409243   f (18) =

1.675092356490104E-017 (формула (18))

x (23) =  1.40441482409243   f (23) =

1.675092356490104E-017 (формула (23))

x (2) =  1.40441482409243   f (2) =

1.675092356490104E-017 (формула (2)).

Пример 1. Если в формуле (18) число слагаемых равно 10, 11, то вычисления дают следующий результат после 5 итераций:

x (18) =  1.40441482409243   f (18) =

1.675092356490104E-017 (формула (18))

x (23) = 1.40441480897897    f (23) =

1.872255664679733E-008 (формула (23))

x (2) =  1.40441498008568   f (2) = -

1.932444457081986E-007 (формула (2)).

Для поиска второго корня выберем точку x⁰ =- 5 для 11 слагаемых в (18) после четырех итераций получим двойную точность корня только по формуле (18):

x (18) = -6.775433974041149E-021 f (18) = -

6.775433974041149E-021 (формула (18))

x (23) = 7.668850082129399E-013 f (23) = = 7.668850082126459E-013 (формула (23))

x (2) = -1.369473868555432E-009 f (2) = -

1.369473869493161E-009 (формула (2)).

Таким образом, точность формулы (18), по сравнению с формулами (2), (23), в случае однократного корня достигается не только в малой окрестности, но и вдали от корня, а алгоритм (18) имеет меньшее число итераций, чем остальные формулы.

В работе [1] в одном из примеров приведено только два слагаемых формулы (18), и показан третий порядок ее скорости, очевидно, в меньшей окрестности корня, чем (18) (однако не указано, как формула была получена).

Для сравнения алгоритмов рассмотрим еще несколько примеров.

Пример 2. Решить уравнение f ( x ) = ( x - 2 ) ³⁰ = 0, x = 2, m = 30, x ⁰ = 7.

В примере 2 единственный корень x=2 имеет кратность m =30.

Достаточно одной итерации для достижения двойной точности в формулах (22) и (23) в случае кратного корня:

x (22) = 2.00000000000000   f (22) =

0.000000000000000E+000

x (2) = 6.83333333333333   f (2) =

3.368235318563970E+020

x (23) = 2.00000000000003 f (23) =

0.000000000000000E+000.

Пример 3. Решить уравнение f ( x ) = ( x - 2 ) ²⁰ = 0, x = 2, m = 20, x ⁰ = 7 .

В примере 3 единственный корень x=2 имеет кратность m =20.

Достаточно одной итерации для достижения двойной точности в формулах (22) и (23) в случае кратного корня:

x (22) = 2.00000000000000   f (22) =

9.332636185032189E-302

x (2) = 6.75000000000000   f (2) =

34187881699423.1

x (23) = 2.00000000000000   f (23) =

9.785978320356312E-296.

Пример 4. Решить уравнение f ( x ) = ( x - 2 ) ³ = 0, x = 2, m = 3, x ⁰ = 7 .

В примере 4 единственный корень x=2 имеет кратность m =3.

Достаточно одной итерации для достижения двойной точности в формулах (22) и (23) в случае кратного корня:

x (22) = 2.00000000000000   f (22) =

0.000000000000000E+000

X (2) = 5.33333333333333   f (2) =

37.0370370370370

X (23) = 2.00000000000000   f (23) =

0.000000000000000E+000.

В формулах (18), (22) как и в формуле (23), используются дважды дифференцируемые функции. То есть, в программе кроме функции задаются ее первая и вторая производные.

Ниже написана программа, в которой все переменные и функции имеют двойную точность REAL (8). Алгоритмом программы в формуле (22) сначала вычисляется ряд 1 - A = 1 - 1-Z,, z = 2 ff /(f'n )2, во вторую оче- редь итерации xn= xn - B(1 - A) = xn - (fn / fn )(1 - 1\).

Таблица . Последовательность итераций корня в примере 1 с начальной итерацией x ⁰ =7 для модифицированной формулы Ньютона (23) и по формуле касательных парабол (18). Второй и четвертый столбцы – значение функции в точке x ⁿ .

n x (23)	f ( x (23) )	x (18)	f ( x (18) )
2.0735875	-1.2736 4	2.1099472	-1.36779
6511538	17410333	3230622	37393976
1.2875550	0.1312556	1.4210163	-2.083984
0496885	8837352	8720559	694E-002
1.3914537	1.5889375	1.4044147	1.1662232
7776958	48E-002	2995105	4069E-007
1.4042775	1.7005758	1.4044148	5.2022188
3291033	54E-004	2409243	640E-015
1.4044148	1.8722556	1.4044148	1.6750923
0897897	64E-008	2409243	56E-017

Из таблицы видно, что после пяти итераций для поиска корня кратности m =1 формула касательных парабол (18) имеет двойную точность (16 значащих цифр), а модифицированная формула (23) дает только семь (достигается только первая точность) верных знаков при одной и той же начальной точке итерации x⁰=7.

В программе на FORTRAN все функции и переменные заданы с двойной точностью, в программе записано условие примера 2: program nuton use dfimsl integer(8),parameter::n=10,m1=30,m=11; integer(8)::i,j;

re- al(8)::x,x0,xx,x10,x20,s,s1,s2,s0,s10,f,f1,f2,q,B,p ,Y1,Y2;

f(x)=(x-2D0)**30D0;f1(x)=30D0*(x-2D0)**29D0;f2(x)=870D0*(x-2D0)**28D0 x=7d0;x0=x;xx=x;x10=x;x20=x;s=0d0;s1=1d0;s 2=5d-1;s0=0d0;s10=1d0

xxx1=-2d0*dfloat(m1-1)/dfloat(m1);

do j=1,m;s10=s10*xxx1*(s2-dfloat(j)+1d0)/dfloat(j);

s0=s0+s10;if(j==m)then;B=s10;else;endif;end do Y2=1d0+s0/dfloat(m1-1);Y1=Y2-B/dfloat(m1-1);

p=Y1/(Y1-

Y2);print*,"Y1=",Y1,"Y2=",Y2,"p=",p do i=1,n,1;xxx=-2d0*f(x)*f2(x)/(f1(x)*f1(x)); s1=1d0;s=0d0;do j=1,m;if(j==m)then q=p;elseif(j<=m-1)then;q=1d0;end if;

s1=s1*xxx*(s2- dfloat(j)+1d0)/dfloat(j);s=s+s1*q;

end do;x=x+s*(f1(x)/f2(x));x10=x10-f(x10)/f1(x10);

x20=x20-f(x20)*f1(x20)/(f1(x20)*f1(x20)-f2(x20)*f(x20))

print*,"i=",i;print*,"x=",x,"f=",f(x);

print*,"xn=",x10,"fn=",f(x10);print*,"x20=",x20, "fx20=",f(x20);

if(dsqrt(f(x)*f(x))<1d-

16)then;print*,"i=",i;print*,"x=",x,"f=",f(x);

print*,"xn=",x10,"fn=",f(x10);print*,"x20=",x20, "fx20=",f(x20);

pause;endif;enddo;end program nuton

Основные результаты в данной работе:

• 1)    Получена модифицированная формула Ньютона – касательных парабол (11).

• 2)    В Лемме 1 доказано, что формула (11) корректна только для случаев кратности корня m =1, m =2. При этом порядок скорости сходимости навязки к нулю в формуле (11) выше первого.

• 3)    В лемме 2 доказан третий порядок скорости невязки в формуле (11) для корня кратности m =1.

• 4)    В лемме 3 доказан второй порядок скорости невязки в формуле (11) для корня кратности m =2.

• 5)    Формула (11) обобщена до формулы (18) на числовой прямой (-∞,+∞) для переменной z и корректна для кратности корня m =1.

• 6)    Получена формула (22) для кратности корня два и выше с параметром 0

• 7)    На примерах показано, что при кратности корня m =1 алгоритм (22) эффективнее алгоритмов (2), (23). Для кратности корня m =3, 20, 30 и простой функции достаточно одной итерации для достижения двойной точности корня по алгоритму (21), (22).

Новые алгоритмы (18), (21), (22) позволят численно решать нелинейные уравнения и системы за меньшее число итераций, чем формула касательных (2). В задачах на собственные значения (случай действительных корней) при анализе обыкновенных дифференциальных уравнений и их систем [6], [7], [8], [9] формулы (18), (21), (22) наряду с алгоритмами (2), (23) могут быть полезными.