Модифицированная ньютоновская динамика (MOND) и ее возможные интерпретации

1.    Введение. Проблема кривых вращения галактик

Одной из главных проблем современной астрофизики является объяснение кривых вращения галактик. Согласно большому количеству накопленных наблюдательных данных, почти во всех известных спиральных и дисковых галактиках скорости звезд и газовых облаков, определяемые с помощью эффекта Доплера, не превышают 300—350 км/с. Центростремительные ускорения этих объектов, траектории которых в хорошем приближении можно считать плоскими и круговыми, также достаточно малы (по крайней мере, за пределами плотного ядра). Все это говорит о том, что движение этих объектов должно описываться в рамках механики Ньютона с лишь малыми релятивистскими поправками. Однако, это не имеет места. Механика Ньютона предсказывает, что скорости галактических объектов должны убывать с ростом расстояния до центра галактики (так называемого галактоцентрического расстояния г). Наблюдения демонстрируют другую закономерность: начиная с некоторого характерного расстояния г о, индивидуального для каждой галактики, скорости объектов выходят на постоянную величину, т.е. практически перестают зависеть от г. То есть, в области r > го наблюдаемые скорости существенно больше предсказываемых механикой Ньютона.

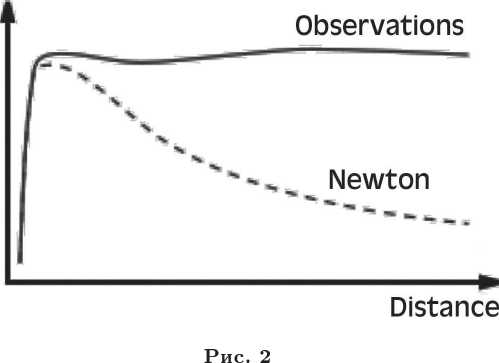
Поясним это на упрощенной модели. Пусть имеется сферически симметричное однородное тело массой М (грубая модель ядра галактики), вокруг которого движется по окружности пробное тело массой m (рис. 1).

Рис. 1

Применяя второй закон Ньютона, закон всемирного тяготения и формулу для центростремительного ускорения

F = ma                                     (1.1)

F

Mm G—т ； ^- r²

(1.2)

и² a =- r

(1.3)

получаем, что вне массивного ядра скорость пробного тела на круговой орбите убывает с расстоянием в соответствии с формулой и =

GM

r

(1.4)

Это показано пунктирной кривой на рис. 2. В то же время, реальные кривые вращения при больших г, как правило, выходят на плато, что схематически показано сплошной кривой на рис. 2 (реальные кривые вращения галактик можно найти во многих обзорах, включая [1-3] и ссылки внутри). Учет полного распределения масс в галактиках не решает проблему. То же самое относится к эллиптическим и сфероидальным галактикам: скорости достаточно удаленных от центра объектов значительно превышают теоретически предсказанные.

^~00_ф>

Имеются два пути решения данных проблем. Первый путь основан на введении так называемой «темной материи», способной обосновать экспериментально наблюдаемые закономерности. Большинство исследователей пошло по этому пути. Однако это означает перекладывание трудности из космологии в физику элементарных частиц, поскольку темная материя другими способами себя никак не проявляет и непонятно, что именно может претендовать на роль материи с такими свойствами. На сегодняшний день можно сказать, что если бы темная материя излучала или поглощала электромагнитное излучение или нейтрино (с достаточной интенсивностью), то она уже была бы обнаружена. Также имеется ряд вопросов, связанных с динамикой темной материи и с ее распределением в галактиках, и вопросы, связанные с устойчивостью галактик [1, 2]. Из всех предложенных кандидатов на роль темной материи на сегодняшний день остаются лишь суперпартнеры некоторых частиц стандартной модели, тяжелые нейтрино и некоторые экзотические гипотетические частицы. Гипотеза о барионной темной материи сталкивается с проблемами применительно к наблюдениям в рамках нашей Галактики, а также к космологии. Более того, недавнее исследование [4] движения более 400 звезд, расположенных на расстояниях до 13000 световых лет от Солнца, не нашло свидетельств присутствия какой-либо темной материи в этом объеме пространства. Таким образом, гипотеза о существовании темной материи сталкивается с серьезными трудностями. Это заставляет задуматься о том, что возможно, сама теория гравитации (как ОТО3, так и нерелятивистская, ньютоновская) нуждается в модификации. Одной из наиболее разработанных таких теорий является модифицированная ньютоновская динамика (MOND).

2.    Основные принципы модифицированной ньютоновской динамики (MOND)

Одним из оснований MOND (М. Милгром, 1983 [5-7], обзоры [1-3,8]) явилась новая обнаруженная в наблюдениях закономерность. Помимо того, что кривые вращения выходят на плато, было обнаружено, что во всех рассматриваемых галактиках отклонения от предсказаний механики Ньютона начинают быть заметными при одном и том же ускорении a° ~ 1О^-10 м/с². То есть, для объектов, движущихся с ускорением, большим а°, механика Ньютона достаточно хорошо работает, а при движении с малым ускорением (меньшим а°) наблюдаются отклонения. В связи с этим возникла идея модифицировать ньютоновскую динамику, введя в рассмотрение новую константу а° с размерностью ускорения (иногда называемую « фундаментальным ускорением»). Было предложено два пути модификации. Первый путь заключался в том, чтобы модифицировать второй закон Ньютона (1.1), оставляя неизменным закон всемирного тяготения (1.2), а второй путь - наоборот.

Для начала рассмотрим первый путь. Второй закон Ньютона можно модифицировать, введя в него дополнительный множитель, зависящий от отношения ускорения тела a к константе a°:

a

F = m 从 (x)a, x = — a0

Этот множитель (называемый интерполяционной функцией или просто мю-функцией) обладает следующими асимптотическими свойствами:

〃 ( x) 仁 1 при x >>  1

(2-2)

〃 ( x) 仁 x при x <<  1

Определенная таким образом мю-функция, или точнее, множество функций с асимптотиками (2.2), приводит модифицированную теорию в согласие с наблюдениями (по крайней мере, в пределах больших и малых ускорений). Для простейшей модели на рис. 1 имеем уравнение:

µ

aa a0

GM r2

(2.3)

В пределе больших ускорений, a >> a°, выполняется обычная механика Ньютона. В пределе малых ускорений. a << a°* во ： зішкает «глубокий MOXD-режпм». для которого характерно следутотттее ：

GMa0 a =------

(2.4)

r и = 4/ GMa0 = const                               (2.5)

То есть, при малых ускорениях скорости объектов перестают зависеть от радиусов их орбит, и кривая вращения выходит на плато.

Более того, формула (2.5) находится в согласии с эмпирически установленным законом Талли-Фишера, который связывает светимость L спиральной галактики с «амплитудой» скорости вращения ее объектов (т.е. со скоростью на плато кривой вращения): L 〜 ut. С другой стороны, светимость пропорциональна полной массе галактики: L 〜 M. Это согласуется с формулой (2.5), из которой следует, масса галактики (если ее приближенно считать равной массе центрального тела М) пропорциональна четвертой степени скорости на плато. Таким образом, закон Талли-Фишера можно считать одним из обоснований MOND.

Существует множество примеров интерполяционной функции 〃 (x), удовлетворяющей условиям (2.2). Наиболее обсуждаемыми в литературе являются т.н. стандартная функция

x

〃(x) = /1 , 2,

V 1 + x2

простая функция

x

〃(x) =    ~,

1 + x а также содержащее их семейство вида x 〃(x)= "....而，

(1 + xn)1/n где n - целое отличное от нуля число. Графики функций (2.6) и (2.7) показаны на рис. 3.

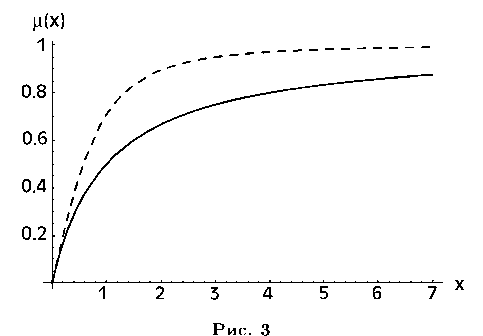
Сплошная линия - график простой функции (2.7). Эта функция, как считается на сегодняшний день [1, 2] позволяет хорошо описывать движение объектов в галактиках на всех масштабах ускорений. Однако, это не очень хорошо согласуется с наблюдаемым движением планет Солнечной системы. Причина в том, что простая функция недостаточно быстро стремится к единице при больших аргументах (т.е. недостаточно быстро выходит на ньютоновский предел). Пунктирная линия - график стандартной функции, которая стремится к единице заметно быстрее, но описывает вращение галактик с меньшей точностью. Можно предположить, что график «оптимальной» функции, находится где-то между этими линиями. Существует ряд попыток найти такую функцию; их обзор, а также ряд примеров, можно найти в обзоре [1].

Что можно сказать о «фундаментальном ускорении» а₀? Из наблюдений следует лишь то, что во всех галактиках отклонения от ньютоновской механики начинаются на одном и том же масштабе ускорений a° ~ 1О^-10 м/с² . Иногда дается оценка а° = 1, 2 • 1О^-10 м/с2, основанная на фитинге MOND реальными данными [2]. Причина такого «совпадения» остается пока неясной. Но важным является уже то, что а₀ универсально для всех галактик, что позволяет говорить о новой универсальной константе.

Более того, оказалось, что величина а₀ каким-то образом связана со свойствами вселенной в целом. По словам Милгрома [9], «... Это приблизительно то ускорение, которое нужно объекту, чтобы разогнаться от состояния покоя до скорости света за время существования вселенной.⁴ Также оно близко к недавно обнаруженному ускорению вселенной^. Из численных соотношений с хорошей точностью следует отметить связь а° с постоянной Хаббла 2па° 仁 H°c, а также с космологической постоянной [3] в моделях, где темная энергия моделируется лямбда-членом. Отсюда вытекает, что космологическое красное смещение может быть эффективно представлено как гравитационное красное смещение в однородном поле с напряженностью 2па₀. Одна из возможных трактовок этого факта основана на теориях с переменной скоростью света (см. классическую работу Р. Дикке [10] или вариации на тему в [11] и ссылках внутри). На наш взгляд, связь а₀ с космологией может говорить о том, что для создания более глубокой теории, воспроизводящей результаты MOND, следует привлечь принцип Маха (см. напр. [12]). Похоже, что применительно к MOND эта гипотеза еще не достаточно исследована и представляет интерес для дальнейшего изучения.

Рассмотрим теперь второй путь построения MOND: модифицировать закон всемирного тяготения, оставляя неизменным второй закон Ньютона. Искомую модификацию можно получить, поделив на мю-функцию равенство5

m" (^) a = GMMm ⑵ 9 )

Тогда слева будет произведение массы на ускорение, а справа будет новое выражение для силы:

F =

GMm 1 r²   " (a/ao)

GMm 1

r2 " (F/ma0)

(2.10)

Явное выражение для силы будет зависеть от конкретного вида мю-функции. Например, для функции (2.7) формула для силы имеет вид:

GMm 2r²

(1+\Я12

(2.11)

где введена величина

/GM ro = V....:

(2.12)

V Q0

задающая характерный масштаб расстояний в данной конкретной галактике.6 Очевидно, что такая формулировка MOND эквивалентна обсужденной выше в случае задачи двух тел. Однако, в случае задачи многих тел, или при наличии других взаимодействий помимо гравитации, эти формулировки будут давать различные результаты. В пределах одной галактики эти формулировки практически неразличимы [8].

«Эффект внешнего поля». Возникает вопрос: можно ли проверить MOND в земных экспериментах, изучая движение тел с малыми ускорениями в земной лаборатории? Ответ зависит от того, будет ли выполняться соотношение вида (2.9) в неинерциальных системах отсчета, если в него добавить силы инерции. В принципе возможен как положительный, так и отрицательный ответ на этот вопрос [1, 2]. Если да, то выполняется сильный принцип эквивалентности. Если нет, то он не выполняется, и имеет место так называемый «эффект внешнего поля». В этом случае MOND нельзя проверить в земных экспериментах в силу того, что Земля движется по орбите вокруг Солнца (во «внешнем поле» Солнца) с центростремительным ускорением около 5,5 ・ 10^-3 м/с², что много больше а 。. То есть, равенство типа (2.9), в общем случае векторное, выполняется лишь в особой космологической системе отсчета, в среднем сопутствующей материи. Милгром и ряд последователей склоняются к такой трактовке теории [1, 2]. Некоторые авторы утверждают, что трактовка, в которой «эффекта внешнего поля» нет, уже опровергнута земными экспериментами.

Одной из трудностей первых вариантов MOND, рассмотренных выше, явилось то, что в них не выполняются законы сохранения (энергии, импульса, момента импульса). Поэтому вскоре Милгром и последователи пришли к выводу [2], что основное соотношение MOND не является точным, а служит приближением какой-то более точной формулы. Попытки найти эту более точную формулу были предприняты на основе лагранжева формализма. Таким образом, одновременно делалась попытка найти более глубокую теоретическую основу для MOND.

• 3.    Лагранжев формализм MOND.

Модифицированная инерция и модифицированная гравитация

Рассмотрим возможные пути к лагранжевой формулировке MOND. Обобщим уравнение (2.3), переписав его в виде

〃(а/а。)а = - V@n(3.1)

где в правой части стоит градиент ньютоновского гравитационного потенциала, удовлетворяющего уравнению Пуассона:

'                                      АФ% = 4nGp(3.2)

Напомним, что если мю-функцию в (3.1) заменить единицей, то имеем соотношения ньютоновской теории гравитации, которые в лагранжевом формализме следуют из лагранжиана вида

L = 一 / [8nG (十Фn) + pФn — p2- d3x rje p — плотность матерші (для спст(?мы точ(?чиых частпті она является о6о6ш,ешюіі(1)уіікттп(?п). и -поле скоростей.

Возможны два способа модификации этого лагранжиана:

• 1.    Модифицировать члены, содержащие характеристики материи. Это привело бы к модификации второго закона Ньютона, что получило название «modified inertia».

• 2.    Модифицировать члены с потенциалом. Это приведет к модификации уравнения для гравитационного потенциала, что стало называться «modified gravity».

Именно второй способ оказался проще и был реализован первым. В работе Бекенштейна и Милгрома [13] была предложена теория, основанная на лагранжиане вида

L = — /| i" 粤) + РФ — 9

d3x

(3.4)

где¹ F — некоторая положительно определенная (функция. Ньтотоиовскпп предел получается при F(X) = X. Варьирование¹ д ( ?пствпя с лагранжианом (3.4) приводит к уравнениям ：

▽ ф

4nGp                              (3.5)

日 =-УФ                                        (3.6,)

Уравнение (3.5) представляет собой обобщение уравнения (3.2) для гравитационного потенциала. Существенным его отличием от (3.2) является то, что оно нелинейно. Мю-функция введена в него посредством следующей замены:

F'(X) 三 〃 (vX)                                  (3.7)

Второй закон Ньютона остается без изменений и в случае чисто гравитационного взаимодействия выражается уравнением (3.6).

Легко показать (это видно непосредственно из лагранжиана (20)), что в этой теории выполняются законы сохранения энергии, импульса и момента импульса. Фактически, эта теория (названная в [13] AQUAL, Аквадратичный Лагранжиан) является наиболее последовательным и обсуждаемым сегодня вариантом MOND. Отметим, что она не может быть опровергнута в земных экспериментах, поскольку гравитационное поле на Земле на много порядков больше а°, и оно не может быть скомпенсировано силами инерции (сильный принцип эквивалентности не выполняется, см. [2]).

Сопоставляя новое уравнение для потенциала (3.5) с уравнением Пуассона (3.2), замечаем, что справедливо следующее соотношение:

▽ Ф

@ 0

Q0

▽ Ф = ▽ ФN + ▽ X h                        (3.8)

где¹ h — некоторое векторное поле. Из те ор емн Гаусса, ii (З.-э) следует, что если вся рассматриваемая система обладает сферической, цилиндрической или плоской симметрией, роторный член равен нулю, и мы имеем прежнее соотношение (3.1). В работах Милгрома и Брады (см. [2] и ссылки внутри) было показано, что для большинства галактик поправка, вносимая роторным членом, не превышает 5—10%. Таким образом установлено соответствие между этой теорией и первыми вариантами MOND.

Другой путь модификации лагранжиана (3.3), «modified inertia», был реализован в работах Милгрома [14, 15], где был модифицирован третий (кинетический) член в квадратных скобках в (3.3). Для каждой частицы этот член был заменен функционалом от всей траектории этой частицы, зависящим также от а° как от параметра. Гравитационный потенциал в этой теории определяется обычным уравнением Пуассона (3.2), в то время как уравнение движения пробной частицы приобретает нелокальный характер и имеет вид:

A[ {尸 (t) } ,r, ao] = -▽ ФN ⑺

(3.9)

rje / — ік?которып (функционал траектории частицы {/ (t) } с раз мерность то ускорения. При боль-тих ускорениях этот функционал совпадает с ускорением частицы, A(r) 心 a(r), а при малых ускорениях он представляется в виде

N守⑴} ,r>0 ^] =5^Qf ⑴ } ， Г

(3.10)

rje Q — некоторый новый (функционал с раз мерность то ква.ді ) а.та. ускорения. Милгром показал, что теории такого типа в общем случае обязательно должны быть нелокальными по времени⁷, чтобы быть галилеевски инвариантными. С другой стороны, он показал, что в случае равномерного движения по окружности (наиболее важный для описания галактик случай) уравнение (3.9)

переходит в

〃 ( a/@0 ) a

dФN dr

(3.11)

Таким образом, этот вариант теории также соответствует первоначальным идеям MOND.

На сегодняшний день установлено, что MOND достаточно хорошо описывает движение объектов в галактиках всех типов [1]. Однако, MOND имеет также и ряд недостатков:

• 1.    В пределах галактик MOND не описывает гравитационное линзирование света. Это - одно из оснований критики MOND в пользу темной материи.

• 2.    MOND недостаточно хорошо описывает динамику на сверхгалактических масштабах (в скоплениях, сверхскоплениях, вселенной в целом). По-прежнему требуется темная материя, однако, плюсом MOND можно считать то, что темной материи требуется меньше (примерно столько же, сколько наблюдаемой).

• 3.    На сегодняшний день отсутствует последовательная релятивистская версия MOND. Имеется ряд попыток построить такую теорию (их обзор можно найти в [1]), но ни одна из них не является общепризнанной. Нерелятивистские версии не претендуют на описание вселенной в целом, не описывают космологическое красное смещение и т.д.

• 4.    MOND остается в некоторой степени феноменологической теорией, и пока не найдено, из каких первичных, более фундаментальных принципов могли бы следовать ее соотношения. Иными словами, не найдена теоретическая основа для MOND.

4.    Реляционный подход к MOND

Попытки найти теоретическую основу для MOND предпринимались различными авторами, начиная с самого Милгрома [8]. К таким попыткам относятся механистические модели [8], мембранные модели [8], «диэлектрическая аналогия» [1], гравитация как энтропийный эффект (ссылки в [3]) и другие. Ни один из этих подходов пока не дал вполне последовательную физическую картину, так что исследования продолжаются. В следующем разделе представлена наша попытка найти теоретическую основу для MOND.

Итак, известные на сегодняшний день варианты MOND можно условно разделить на два направления: модифицированная инерция и модифицированная гравитация (хотя граница между этими понятиями является весьма тонкой, как отмечено в [8]). Ниже будет представлен принципиально новый подход к интерпретации MOND на основе реляционных представлений о пространстве и времени [16, 17, 18].

Главная идея реляционного подхода состоит в том, что пространство и время - это существенно макроскопические понятия. Понятия пространства и времени проистекают из опыта чувственного восприятия и справедливы лишь при описании макроскопических явлений, в то время как в микромире эти понятия теряют смысл. Микромир состоит из некоторых более элементарных объектов, а пространство-время формируется статистически в результате усреднения множества отношений между этими объектами. Непрерывное пространство-время - это лишь приближение, тогда как микромир состоит из объектов с принципиально иными свойствами. Яснее всех, вероятно, эту мысль выразил Луи де Бройль [19]:

«Понятия пространства и времени взяты из нашего повседневного опыта и справедливы лишь для явлений большого масштаба. Нужно было бы заменить их другими понятиями, играющими фундаментальную роль в микропроцессах (...). Однако пока мы не добились успеха в распространении наших представлений в указанном направлении, мы должны стараться с большими или меньшими трудностями втиснуть микроскопические явления в рамки понятий пространства и времени, хотя нас все время будет беспокоить чувство, что мы пытаемся втиснуть алмаз в оправу, которая ему не подходите.

Одна из главных задач реляционного подхода заключается в том, чтобы вывести пространственно-временные понятия из некоторой реляционной теории микромира при помощи некоторой статистической процедуры, подобно тому, как понятия температуры или давления определяются на основе представлений о движении и взаимодействии частиц в молекулярно-кинетической теории. Более того, свойства пространства-времени (размерность, сигнатура, метрические свойства и др.) могут и должны быть выведены на основе этой пока предполагаемой реляционной теории. Здесь в игру вступает принцип Маха. Реляционный подход неразрывно связан с принципом Маха, поскольку сами понятия расстояний и промежутков времени определяются через множество отношений между объектами рассматриваемой системы и всей остальной вселенной. Подобную точку зрения можно встретить, например, в известной монографии П. К. Рашевского «Риманова геометрия и тензорный анализ» [20]:

^Возможно, что и сам четыре хмерный пространственно-временной континуум с его геометрическими свойствами окажется в конечном счете образованием, имеющим статистический характер и возникающим на основе большого числа простейших физических взаимодействий элементарных частиц. Но, конечно, подходы к этому вопросу должны носить совсем иной характер, поскольку они должны базироваться на квантовой механике - теории совершенно иного стиля, чем теория относительности^.

Поскольку пространство имеет вторичный характер по отношению к некоторым объектам микромира, может оказаться так, что расстояния между астрофизическими объектами (те, что входят в закон всемирного тяготения и формулу центростремительного ускорения) отличаются от значений, получаемых нами в наблюдениях с Земли. На этом основана предлагаемая в этой работе интерпретация MOND, которую можно условно назвать «модифицированным расстоянием» («modified distance»).

Более конкретно, наше предположение состоит в том, что второй закон Ньютона и закон все мирного тяготения сохраняют свой вид в модифицированных координатах, которые отличаются от классических. Пусть 己一модифицированный радиус-вектор некоторого объекта (звезды или газового облака) в галактоцеитрической системе отсчета, а 戸一классический (наблюдаемый с Земли).

Тогда можно записать:

ma* = F

GMm

， *

(4.1)

где М - масса ядра галактики (рассматриваем упрощенную модель на рис. 1), т - масса рассматриваемого объекта; все величины со звездочками - модифицированные. Модифицированные скорость и ускорение определяются как

U*

dr* dt

d2r* dt2

(4.2)

Если орбиту считать окружностью, то для ускорения имеем

a*

U2

∗

(4.3)

Будем полагать, что модифицированное расстояние г* является некоторой функцией от классического расстояния г:

Г* = f ( г )                                             (丄 1)

Возникает вопрос: как связана модифицированная скорость и* с классической скоростью и? Напомним, что классическая скорость измеряется по доплеровскому сдвигу спектральных линий, а расстояние измеряется по углам. Рассмотрим две гипотезы о связи модифицированной и классической скорости.

Гипотеза 1. Модифицированная и классическая скорости совпадают: и* = и.

Гипотеза 2. Модифицированная и классическая угловые скорости совпадают: ® = ^* =争, где¹ T — п ( ?ріюд обраттіеішя данного объекта вокруг п,етітра галактики⁹. Тогда, можно записать ： и* = г* ^*. и = г^. откуда

и * = ^ и =产 и

(4.5)

Выясним, какой может быть функция f (r) в рамках первой и второй гипотез. Будем исходить из того, что известно из MOND (и из наблюдений). При больших ускорениях (или при малых расстояниях) должна реализовываться механика Ньютона, поэтому f (r) 心 r. При малых ускорениях (больших расстояниях) классическая скорость должна выходить на константу в соответствии с (2.5). Конкретный вид асимптотики f (r) при больших г зависит от того, какую гипотезу о связи и ii и* мы примем.

Рассмотрим гипотезу 1: и* = и. В этом случае имеем:

υ2  GM 2 GM  GM

=, U =     =

r*      r2            r*      f (r)

При больших расстояниях и² = ， GMa° = const, откуда получаем f (r) = у G^ = const.

Получается необычный результат: все объекты, скорости которых находятся на плато кривой вращения, находятся на одном и том же (или почти одном и том же) модифицированном расстоянии от центра галактики. Если, тем не менее, принять эту гипотезу, то легко найти следующие примеры

(j)yilKTIIIII r* = f (r):

r* = r (1+ (Л

(4-6)

где n — отличное от нуля вещественное (не обязательно целое) число, а характерное расстояние го определено формулой (2.12).

Рассмотрим гипотезу 2. Выражая модифицированную скорость через классическую, имеем:

υ2    υ2r     GM             2         r2           r2

——к- — 72- •。工 к 〉 Да и — GM гз — GM f ( rp

При больших『：                         _____ и2 = GMao = const, f3(r) r2

GM

≡ r0 , a0

f (r) = V ror2.

Таким образом, в рамках гипотезы 2, r* =

Примеры таких функций:

r* = r

r,    r<< r0

√3 r0r2,  r>>r0

卜+

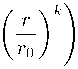
1—

3k

(4-7)

где к - отличное от нуля вещественное число. Заметим, что между формулами (4.6) и (4.7) имеется взаимно однозначное соответствие: при п = к они приводят к одинаковой зависимости классической скорости от классического расстояния, а именно

υ

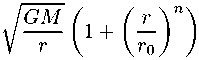
₂1 _n

(4.8)

В силу этого обстоятельства во всех вопросах, связанных с наблюдаемыми кривыми вращения галактик, достаточно рассматривать лишь одну из гипотез (1 или 2). Будем в дальнейшем рассматривать гипотезу 1. Отметим, что в рамках гипотезы 1 модифицированное расстояние имеет максимальное значение r* max = r°, индивидуальное для каждой галактики, и не может принимать больших значений. Возможный физический смысл этого еще предстоит проанализировать.

Возникает вопрос: при каком значении п формула (4.8) наилучшим образом соответствует наблюдениям? Простейшим критерием является сопоставление с MOND: нужно найти такое п, при котором график функции (4.8) лежит между аналогичными графиками MOND, получаемыми с помощью интерполяционных функций (2.6) и (2.7).

Рассмотрим соотношение (4.8) при различных целых значениях п и выясним, какое из этих значений дает наилучшее согласие с классическим милгромовским вариантом MOND. В разделе 2 говорилось о том, что MOND описывает реальные галактики с различной степенью точности при различном выборе интерполяционной функции 〃. Наиболее обсуждаемыми являются стандартная функция (2.6) и простая функция (2.7), и считается, что оптимальная функция лежит между ними. Соответственно, задача заключается в том, чтобы найти такое п (если оно существует), при котором модельная кривая вращения (4.8) лежит между аналогичными кривыми, получаемыми в MOND с помощью формул (2.6) и (2.7). Для этого рассмотрим упрощенную модель, показанную на рис. 1. Пусть ядро галактики моделируется однородным шаром радиуса 0,5г°. Для начала построим кривые вращения MOND, соответствующие стандартной и простой мю-функциям, и сравним их с ньютоновской кривой вращения (рис. 4). На рис. 4 показаны графики зависимости обезразме-ренной скорости (v° — скорость на плато) от обезразмеренного расстояния. Верхняя черная линия соответствует простой функции (2.7), средняя черная линия - стандартной функции (2.6), а нижняя серая линия - механике Ньютона. График искомой оптимальной функции должен лежать в коридоре между черными линиями. При рассмотрении области внутри ядра в качестве массы М берется масса вещества, заключенного внутри шара радиуса г, т.е. M = M(r).

На рис. 5 показаны те же две кривые вращения MOND, что и на рис. 4, а также три кривые, получаемые с помощью формулы (4.8) при n = 1, 2 и 3. Участок, представляющий наибольший интерес, показан в укрупненном масштабе по сравнению с рис. 4; ньютоновская кривая не показана. Верхняя пунктирная линия соответствует 几= 1, точка-пунктир — n = 2, а мелкий пунктир — n = 3. Видим, что в коридоре между черными линиями лежит график функции, соответствующий n = 2. При п = 1 график лежит заметно выше обеих черных линий, а при n = 3 график почти совпадает с соответствующим стандартной функции, но при достаточно больших г лежит чуть ниже него (что не очень хорошо соответствует реальным кривым вращения, как отмечалось в [1, 2]). Таким образом, приходим к выводу, что наилучшее соответствие наблюдениям дают формулы (4.6) и (4.8) при п = 2.

0>>-q-LQOdoJD нен 工① d ① wmedm① 9。

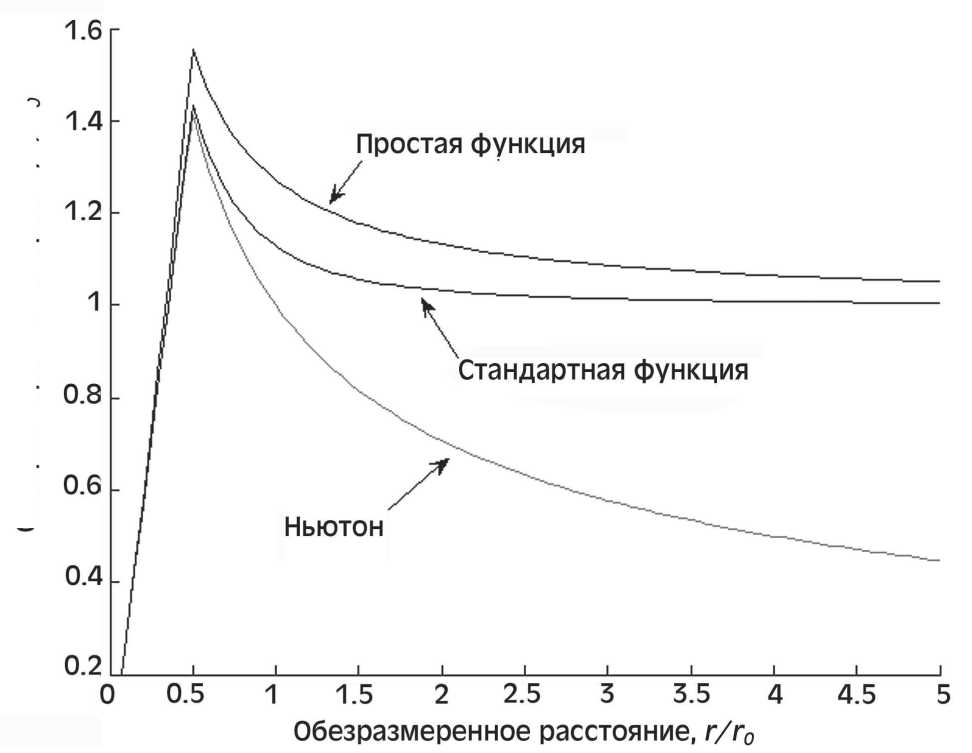
Рис. 4. Сопоставление кривых вращения MOND и ньютоновской кривой вращения.

5.    Отклонение лучей света массивным телом в реляционном варианте MOND

Одной из проблем всех известных до сегодняшнего дня нерелятивистских вариантов MOND является невозможность корректного описания отклонения лучей света массивным телом. Как из вестно, этот эффект имеет корректное количественное описание в рамках ОТО. В метрике Шварц шильда угол отклонения луча света, если он достаточно малый, рассчитывается по формуле (см.

напр. [21, 22]):

_ 4GM

(5.1)

• =^2R

где M — масса центрального тела, а R — расстояние от центрального тела до точки пересечения луча с его осью симметрии. Этот результат хорошо подтвержден наблюдениями. В то же время

07/7 -qluodoM。^гахтфаф?-тгаатфюо

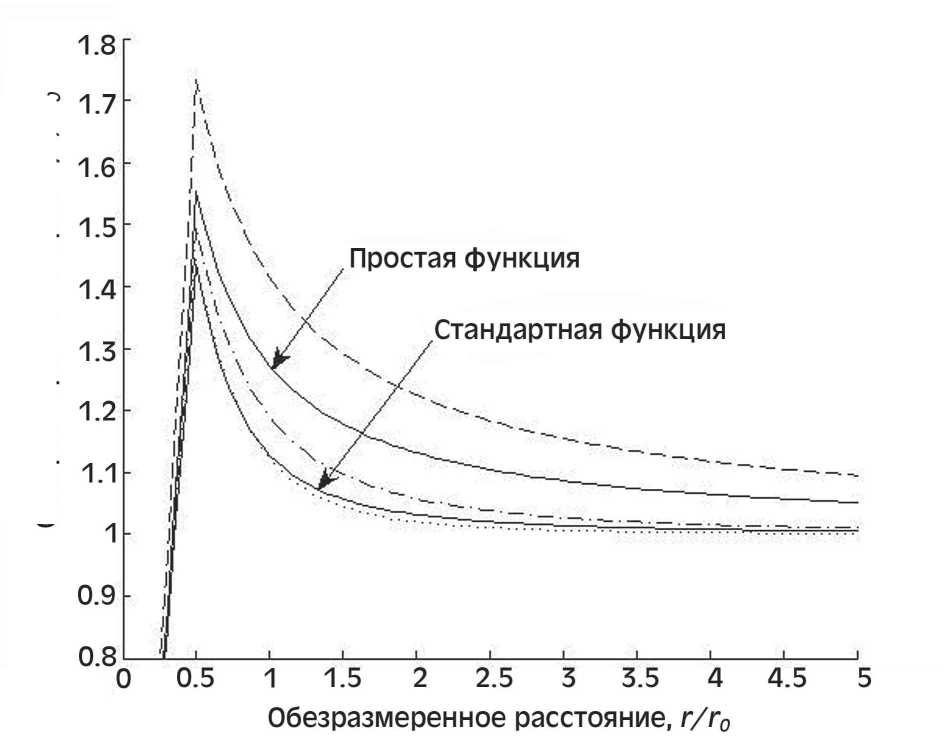
Рис. 5. Сопоставление кривых вращения классического и реляционного варианта MOND. Длинный пунктир -формула (4.8) при n = 1; точка-пунктир — 〃 = 2; короткий пунктир (точки) - п = 3.

в рамках нерелятивистской ньютоновской механики, считая фотон классическим пробным телом, можно также получить эффект отклонения лучей света, но этот эффект ровно в два раза меньше:

2GM

(5 ・ 2)

Оказывается, однако, что вычисление подобного эффекта в рамках развиваемого нами реля

ционного варианта MOND приводит к нетривиальному результату. Если расстояние R порядка или больше величины r° для данного гравитирующего центра, то наблюдается существенное от

клонение от формулы (5.2) в большую сторону, и при некоторых значениях R воспроизводится правильная формула (5.1).

Чтобы прийти к этому результату, нужно учесть, что формула (5.2) записывается в модифицированных координатах (обозначенных в разделе 4 переменными со звездочкой), которые, по нашей гипотезе, отличаются от классических. То есть, что в формулу вида (5.2) входит модифицирован

ное расстояние R*:

θ

2GM c²R ∗

(5.3)

Перейдем от модифицированных координат к классическим по

формуле (4.6) при найденном

нами оптимальном значении 几= 2:

R* =

R

¹⁺RR 2

(5.4)

Имеем:                                      ______

" 2GM / R²                                , 、

”     + 总                  (S'

Видим, что угол отклонения, вычисленный по формуле (5.5), больше вычисленного по формуле (5.2) в k = У1 + R²/г2 раз. При R = го имеем различие в ^2 раз, а при R = V3r 。 имеем различие в два раза, т.е. при таком R воспроизводится формула (5.1). При больших R (напомним, что характерный радиус галактического диска в несколько раз больше r°) различие существенно.

Более того, при R >> r° имеем предел

θ

2GM  2 V GMao

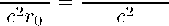
(5.6)

те угол отклонения практически перестает убывать с ростом R и выходит на константу. Отметим, что формулу (5.5) можно переписать в виде

2GMeff ^ө —   c²R ,

R2

Meff = M\ /1 + Т2 r₀

(5.7)

где для сходства с формулой (5.2) введена «эффективная масса» Meff, которая больше наблюдаемой. Это следует учитывать при интерпретации наблюдений гравитационного линзирования света галактиками. Для того, чтобы линзирование имело правильное количественное описание в рамках ОТО, приходится вводить в рассмотрение темную материю. Более того, наблюдение линзирования является сегодня одним из важных методов, позволяющих, как считается, определить распределение темной материи. Однако в развиваемом здесь реляционном варианте MOND «эффективная масса», введенная для сопоставления с ньютоновской теорией и ОТО, может быть в 5-10 раз больше наблюдаемой. Поэтому при описании линзирования света галактиками нет необходимости во введении темной материи.

Заметим, что если проводить все те же рассуждения для соотношения (4.6) при n = 1, то мы получим, очевидно, k = A， Meff = МГ； (5-8)

Разумеется, предложенная модель является упрощенной и применимой лишь для сферически симметричного распределения масс. Однако мы предполагаем, что она может быть обобщена. Идея о том, что классическое расстояние в галактиках не равно модифицированному, может быть формально реализована, если допустить, что пространство вблизи гравитирующих источников обладает эффективным показателем преломления, подобно тому, как это рассмотрено в работе Дикке [10] (см. также вариации на эту тему в [11]). Мы надеемся, что в будущем удастся построить релятивистскую теорию, основанную на реляционных представлениях о пространстве и времени, воспроизводящую результаты MOND, а также все классические эффекты общей теории относительности.

В заключение мы хотели бы выразить благодарность А.В. Соловьеву и С.В. Болохову, а также

В.В. Аристову за плодотворное обсуждение затронутых в данной работе вопросов.