Модифицированная скрытая марковская модель для распознавания речевых сигналов

Цель, которую ставили перед собой авторы статьи, заключалась в создании программного обеспечения для системы распознавания речи в среде Windows, которое использует ресурсы персонального компьютера и работает с речевым сигналом, поступающим с микрофона. Областью применения данной программы является реализация функций удаленного управления компьютером, ввода данных, организация телефонного номеронабирателя. Программа должна распознавать отдельные команды либо последовательности из нескольких слов.

При распознавании слов и их последовательностей наиболее эффективным и часто используемым подходом является применение скрытых марковских моделей (СММ). Этот метод позволяет для распознаваемой последовательности вычислить вероятность ее соответствия настроенной СММ эталонной последовательности.

Свойством СММ является зависимость вероятности последующего состояния модели от текущего состояния, но не от предыдущих состояний модели. Однако в применении к задаче распознавания речи это свойство является недостатком, так как речь не является марковским процессом, а информация о предыдущих состояниях модели важна при распознавании речи.

Для решения этой проблемы объединяют пары, тройки либо последовательности из N состояний модели и используют их как состояния новой СММ. При этом значительно увеличивается количество состояний модели и, соответственно, квадратично растет размерность матрицы перехода состояний. Поэтому авторами была предложена модифицированная СММ, отличающаяся от известных моделей компактным способом хранения информации о вероятностях перехода как между состояниями, так и между последовательностями состояний СММ. Суть модификации заключается в хранении и обработке информации в орграфе. Это позволяет уменьшить необходимый объем памяти и количество выполняемых операций.

В классических СММ вероятность генерации последовательности состояний существенно зависит от начальных шагов алгоритма Витерби. Если на первых шагах алгоритма распознаваемый сигнал был плохо распознан, были допущены ошибки сегментации либо сигнал был некачественно записан, то это существенно повлияет на результат распознавания. В связи с этим был предложен модифицированный алгоритм Витерби, начинающий работу не с начала распознаваемой последовательности, а с элемента последовательности с максимальной дисперсией принадлежности к классу. Это позволило уменьшить вероятность ошибки распознавания.

Ввод и предобработка сигнала. Ввод речевого сигнала осуществляется с помощью микрофона или из файла с частотой дискретизации 8 кГц, разрядность -16 бит.

Для выделения речевого сигнала из пауз и шума вычисляется уровень энергии сигнала и число нулей интенсивности, их среднее значение, дисперсия и пороговые значения [1].

Далее речевой сигнал делится на Т равных частей, перекрывающихся на 2 / 3 (для предотвращения потери информации на границе сигнала), а затем выполняются преобразования внутри каждого сегмента. Для снижения граничных эффектов, возникающих в результате сегментации, каждый сегмент умножается на оконную функцию Хэмминга [2].

Для каждого сегмента вычисляются характеристические признаки речевого сигнала: кепстральные коэффициенты С₁, ..., С_кс, дельта-параметры АС₁, ..., АС_кс, нули интенсивности Z, мгновенная энергия сигнала Е [3].

Для каждого сегмента формируется вектор признаков y = ( C _p..., C nc , А C _p..., А C nc , E , Z ) . (1)

Каждый речевой сигнал представлен последовательностью векторов^, ...,yT.

Затем необходимо разбить пространство векторов признаков на М кластеров. Для этого на основе большого количества речевых сигналов формируется пространство векторовпризнаков {y₁, ...,у_ку}, которое разбивается на М кластеров с центрами {v^ ..., v_M}. Кластеризация производится алгоритмом «к-средних» (k-теак) в евклидовом пространстве [2].

Каждому распознаваемому вектору признаков ставится в соответствие ближайший центр кластера:

y ^ v , m = arg(mindist( y , v )). (2)

i = 1... M

Алгоритмы распознавания. Речь является процессом, изменяющимся во времени. Различные произношения одного и того же слова обычно имеют разную длительность, а слова одинаковой длительности могут отличаться в центральной части из-за различной скорости произношения.

Поэтому для сравнения последовательностей векторов используются специальные алгоритмы, позволяющие сравнивать последовательности векторов различной длины и давать оценку степени принадлежности распознаваемого вектора к одному из эталонов, такие как алгоритм динамического искажения времени (ДИВ) (DyKamic Time WrappiKg, DTW) и скрытые марковские модели (HiddeK Markov Models, HMM) [3].

Скрытые марковские модели. Пусть задано V = {v1,..., vM} - множество наблюдаемых объектов (кла- стеризованные векторы параметров); S = {S1,..., SN} -множество состояний модели (фонемы); Q = {q1,..., qT}, qt е S - состояние модели (фонемы) в момент времени t; O = {о1,..., oT} о е V -наблюдаемая последовательность (векторы параметров); п = {пi}, пi = P(qi = Si) - вероятность начального состояния .; A = {aij}, aij = P(qt = Sj qt -1 = Si) - вероятность перехода Si .Sj; B = {bj(k)}, bj(k) = P(o, = vk\q, = Si) - вероятность принадлежности v к Si.

Тогда кортеж % = ( A, B , п ) называется скрытой марковской моделью.

Скрытые марковские модели позволяют для заданной модели % = ( A , B , п ) и последовательности O = { о 1 , ..., o_T } подсчитать вероятность P ( O | % ) порождения последовательности наблюдений O = { о 1 ,..., o_T } моделью % и наиболее вероятную последовательность Q = { q 1 , ..., q_T } [4].

Пусть даны последовательность наблюдений O = { о 1 ,..., o_T } имодель % = ( A, B , п ) . Алгоритм Витерби используется для того, чтобы выбрать последовательность состояний Q = { q 1 , ..., q_T } , которая с наибольшей вероятностью для данной модели P ( O | % ) генерирует последовательность наблюдений O = { о 1 ,..., o T } [4].

Алгоритм Витерби состоит их нескольких этапов:

• 1.    Инициализация:

• 2.    Цикл по z = 1,..., М:

5 1 ( i ) = п , Ь , ( o j, цД j ) = 0, 1 <  i <  N .     (3)

5, ( i ) = max ( 5,_Д i ) a ) b ( o, ), 1 <  j <  N , t = 2,..., T , (4)

1 < i <  N

• V t ⁽ j ) = ^arg ^max (⁵ 1 - 1 ⁽ i ) ^a j ) .

• 3.    Конец цикла:

• 4.    Восстановление оптимальной последовательности состояний (обратный проход):

1 < i <  N

P ( O | % ) = max( 5 ( i )) , 1 < i <  N ¹

где P ( O | % ) - наибольшая вероятность наблюдения последовательности O = { о 1 ,..., o_T } , которая достигается при прохождении некоторой оптимальной последовательности состояний Q = { q 1 ,..., q_T } , для которой к настоящему времени известно только последнее состояние:

q_T = arg max ( 5 _T ( i ) ) .               (6)

1 < i <  N

• q , =Ц , ( q , + 1 ), t = T - 1, T - 2,...,1 .         (7)

Лево-правой СММ называется СММ, в которой порядок следования объектов последовательности идет слева направо (а . b . с . d, стрелка указывает порядок следования).

Право-левой СММ называется СММ, в которой последовательность следования объектов обратная - справа налево (а ^ b ^ с ^ d).

Вероятность следования за объектом а объекта b обозначим как_р_аЬ:

/' .■/'..■/'■. - для лево-правой СММ;

^- P ab / . .■ /■.■ ^Я ^пр^{аво-левой СММ}.

Применение скрытых марковских моделей для распознавания слов. Для словаря из и слов S₁, ..., S _n , каждое из которых может быть представлено одним или несколькими эталонами слов О₁, ., О_т, обучается своя СММ % ₁, ., % _и.

Для распознаваемой последовательности векторов О и моделей %1, .., %и вычисляется максимальная вероят- ностьР(О|%.),7-1,...,и[4]:

I = arg(max( P ( O | % i ))), i = 1,..., n . (8)

Результатом распознавания является слово, соответствующее данной СММ % . , z = 1, ..., и, с максимальной вероятностью Р(О I % . ), z = 1,..., и.

Модифицированный граф переходов скрытой марковской модели. Как уже отмечено выше, свойством СММ является зависимость вероятности последующего состояния модели от текущего состояния, а не от предшествующих состояний модели, что применительно к задаче распознавания речи является недостатком, так как речь не является марковским процессом. Для распознавании речи информация о предыдущих состояниях модели имеет большое значение.

Для решения этой проблемы объединяют пары S’ = S₁S₂, тройки S’ = S₁S₂S₃ либо последовательности из N состояний модели S’ = S₁S...S_W и используют их как состояния новой СММ. При этом сильно увеличивается количество состояний модели и, соответственно, квадратично растет размерность матрицы переходов состояний А = {а^.}, а ._ = P(q _t = S _j Iq _t _ ₁ = S . ), которая хранит все возможные комбинации переходов [4].

Поэтому было предложено хранить информацию о переходах состояний не в таблице, а в виде СММ-графа. В этом случае в графе хранится информация только о существующих связях, а не обо всех возможных переходах, как в матрице перехода А. Благодаря такой реализации уменьшается необходимый объем памяти и количество выполняемых операций, так как учитываются только существующие переходы между состояниями.

Обычно СММ изображают в виде графа, в котором вершины - это состояния модели, а нагруженные дуги -это вероятности перехода между состояниями (рис. 1).

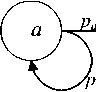
аа

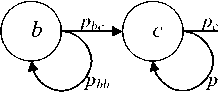
Рис. 1. Схематическое изображение лево-правой СММ

сс

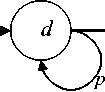
Разработанная реализация СММ в виде орграфа состоит из вершин, одна часть которых соответствуют состояниям СММ, а другая часть - вероятностям перехода между состояниями, и нагруженных дуг, соединяющих их (рис. 2).

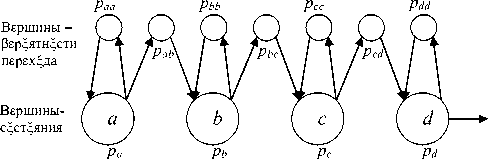
Рис. 2. Схематическое изображение реализации лево-правой СММ в виде орграфа

Вершины U_k, k = 1, .., К орграфа характеризуются следующими параметрами:

• -    вершины-состояния S . : x_t(k) =p (i) - вероятностью наблюдения состояния S . в момент времени t; u_t(k) - текущим значением вершины k в момент времени t;

• -    вершины - вероятности перехода из состояния г в состояние./: х(к) = а. . - вероятностью перехода из состояния I в состояние,/, а. . = P(q_t = 5 - \q _{t- 1} = 5.); u(k) - текущим значением вершины к в момент времени t.

Дуги 1А связывают вершины U и U. Вес дуги W.. w = 1, если вершины U. и Цсвязаны, и w = 0 в противном случае.

Благодаря такой схеме реализации возможно вычисление вероятности P(O \ % ) порождения последовательности наблюдений O = {о₁, „., o_T} для модели % = (Л, В, п ) и последовательности состояний Q = {q₁, ., q _T }, в точности равной вероятности, вычисленной классической СММ.

Так как в граф добавилось (T- 1) вершины - вероятности перехода, то для порождения последовательности наблюдений O = {о₁, ., о_т} длиной T необходимо время t₂ = 1,.,2T-1.

Алгоритм вычисления вероятностиP(O | % ) состоит в пересчете текущих значений u_t(k) вершин U _k в течение времениt₂ = 1,..., 2T- 1.

Значение вершины u . (t) в момент времени t₂ = 1, ., 2T-1 вычисляется аналогично алгоритму Витерби для полунепрерывных СММ [4]:

« 1 ( i ) = ^ 1 ( j ) u j ⁽ ° 1 )>¹ <  i <  K .

^и, ⁽ i ) = max ( u¹ 2 — i ⁽ i ) w j ) b j ⁽o° *- 2 ) ^x * ^{2 ( j} )’ ¹ < ^j <  K * ¹² = ²’ "■’^{(2 T — ])}’(⁹)

P = max ( u 2 t — 1 ⁽ i ) ) .

1 < i <  K

Значения x _{f 2} (k) у вершин - вероятностей перехода остаются неизменными: х(к) = а.., а у вершин-состояний значения х (к) изменяются в моменты времени t’₂ = 1, 3, 5,.,2Т-1:

x 2,Д k ) = p, ( i ), * = 1, .„, T . (10)

Максимальное из текущих значений вершин-состояний max(u_2T-1(k)), к= 1, .., К, в момент времени 2T - 1 равно вероятности Р(О \ % ) порождения последовательности наблюдений О = {о₁, ., o_T} для модели % = (Л, В, п ) и последовательности состояний Q = {q₁, ., q_T}, и является выходом модели:

P ( O | % ) = max ( и 2 т — 1 ( i ) ) . (11)

1 < i <  K

Модификация скрытой марковской модели. Назовем последовательность из А объектов последовательностью длины А, а СММ, учитывающую информацию о последовательностях длины А- СММ уровня А. СММ-граф, описанный выше, будет являться СММ уровня 2.

Реализация СММ в виде орграфа позволила учитывать вероятности перехода не только между двумя состояниями вида а ^ Ъ, но и между последовательностями состояний произвольной длины А вида аЬс ^ d.

СММ-граф уровня 3 реализуется в виде надстройки над орграфом СММ уровня 2. Например, пусть дана последовательность аЪс. СММ-граф будет состоять из вершин { С, U ’ , U^c, V*, и^Ъс, U^аЬс} и дуг, соединяющих их. Вершина W связана с V и U * , а вершина U * ^c - с U и U^c.

Вершина U^e вероятностью,р_аЬс =р _аЬ^_с⁼ Р^_с\_аЬ) имеет входящую дугу от вершины U^аЬи исходящую дугу на вершину U^ (для лево-правой СММ).

Для право-левой СММ вершина U^e вероятностью Р _аЬс Р* _:. ■ Р*._:- имеет входящую дугу от вершины А" и исходящую дугу на вершину U^aЬ.

Вершины уровня А + 1 с информацией о последовательностях длины А + 1 надстраиваются над орграфом СММ уровня А аналогичным образом (рис. 3).

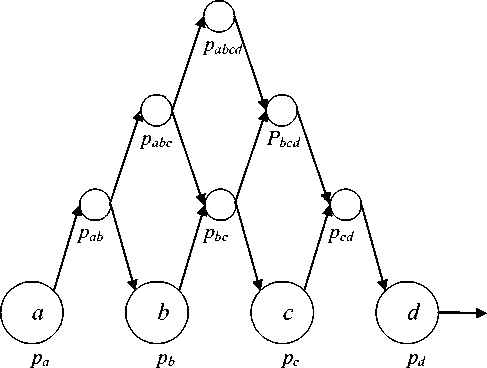
Рис. 3. Схематическое изображение реализации лево-правого

СММ-графа уровня 4 для последовательности аЪсd длиной 4

Значение вершин u . (t) 1-го и 2-го уровней вычисляются аналогично СММ 2-го уровня по формулам (9).

Значение вершин u . (t) уровня 3, ., Ав момент времени t₂ = 1, ..., 2T- 1 вычисляется следующим образом:

low

r * ₂   ⁽ i ) =

¹ scZh( и, 2 _ 1 ( z ⁾ w >  0), 0, иначе.

где r^ — значение Рх^дяю ей дуги с нижнег^ ур^Рня;

r * h^,s^ht ( i ) = и * 2 — 1 ( i ) w j — значение Рх^дяюей дуги с Рерхнег^ ур^Рня;

u * ( i ) = max ( r * ₂ ^h,ght ( i ) ) r * 2 ^ow ( i ) b j ( o * ₂ ) p * 2 ( j ), 1 <  j <  K , * 2 = 2,...,2 T — 1.

Алгоритм надежного старта. В классических полунепрерывных СММ, где вероятности наблюдаемых символов задаются непрерывной функцией распределения, вероятность Р(О| % ) зависит от начальных шагов алгоритма Витерби (прямого либо обратного хода). Если сигнал был плохо распознан, были допущены ошибки сегментации либо сигнал был некачественно записан, то это существенно повлияет на качество распознавания [2].

Поэтому авторами был предложен модифицированный алгоритм Витерби, названный алго^и^мом надежного старта, отличающийся от исходного алгоритма тем, что он начинает работу не с начала распознаваемой последовательности, а с элемента с максимальной дисперсией вероятности D(p _t (i)) принадлежности к классу 5 . :

max_o = arg(max( D ( p ( i )))), i = 1,..., M . (13) = 1,..., т

Элемент O_maxD последовательности O₁, ., O_T с максимальной дисперсией вероятности D(p_t(.)), . = 1, ., М, t = 1, ., Tназван наилучше распознанным элементом последовательности (рис. 4). Предполагается, что элемент хорошо распознан, если вероятность принадлежности к одному из классов существенно отличается от остальных, и плохо распознан, если эти вероятности принадлежности равны и нельзя с уверенностью сказать, к какому из классов принадлежит элемент.

После определения элемента с максимальной дисперсией вероятности D(p(l)) распознаваемая последовательность делится на две подпоследовательности: от начала до OmmD элемента и от OmmD элемента до конца последовательности:

^{0 1} = { 0 1 ,..., О max D },                   (14)

⁰ = ^{{ 0} max D , ..., ⁰ T ^},

Р ^{1 (} j ) = { Р 1 ⁽ j X ..., P max _D ⁽ j )}’ j = ¹ -’ ^{M ,} t = ¹ -’ max D , (15)

P 2 ⁽ j ) = { P max _D ⁽ j X -> P T ⁽ j )}, j = ¹ -> ^M , t = ^maX D , -, ^T .

Для первой последовательности O¹ с помощью алгоритма обратного хода [4] вычисляется вероятность P¹(O¹1 % ).

Рис. 4. Схематическое изображение порядка вычислений, начиная с O _maxD элемента

Для второй последовательности O²вероятность P²(O²1 % ) вычисляется также с помощью алгоритма прямого хода [4].

Общая вероятность последовательности P(O | %) вычисляется как р (о | %) = p 1( оЧ %) • p 2( о 2| %). (16)

При использовании модифицированного алгоритма за счет изменения точки начала алгоритма и сокращения длины подпоследовательностей уменьшается ошибка распознавания. Данный алгоритм может применяться как для разработанных СММ-графов, так и для классических полунепрерывных СММ.

Результаты. Предложенные в данной статье СММ были реализованы, протестированы и сравнены с широко используемыми классическими СММ (см. таблицу). В качестве наблюдаемых объектов классической СММ использовались триграммы (последовательность из трех фонем). Тестирование проводилось на основе речевого корпуса из 40 слов - числа 0,1, ...,20, 30,..., 100,200, ..., 1 000. Обучающая выборка - 40 слов. Тестовая выборка -400 слов.

Модифицированная скрытая марковская модель-граф позволила снизить ошибку распознавания слов в тестовых наборах данных с 15 до 13 % и на 12 % сократить время распознавания по сравнению с классической СММ. Использование алгоритма надежного старта уменьшило ошибкураспознавания с15до9%. Совместное применение СММ-графа и алгоритма надежного старта позволило уменьшить в 2 раза (с 15 до 7 %) ошибкураспознавания слов в тестовом наборе данных и на 12 % сократило время распознавания по сравнению с классической скрытой марковской моделью.

Таким образом, предложена модифицированная скрытая марковская модель на основе орграфа, отличающаяся от известных способом хранения данных и алгоритмом вычисления. Это позволяет использовать информацию не только о вероятности следования отдельных состояний модели, но и о вероятности следования последовательностей этих состояний произвольной длины, а также сократить требуемый объем памяти и время работы алгоритма.

Предложен модифицированный алгоритм Витерби, подходящий как для разработанных СММ-графов, так и для классических СММ и позволяющий уменьшить ошибку распознавания.

Разработанные алгоритмы позволили в 2 раза (с 15 до 7 %) уменьшить ошибку распознавания слов в тестовых наборах данных и на 12 % сократили время распознавания.

Предложенные алгоритмы могут применяться как в области распознавания речи, так и в других областях, где используются скрытые марковские модели, таких как распознавание изображений, обработка сигналов и т. д.