Модифицированный метод Галеркина для уравнения смешанного типа второго порядка и оценка его погрешности

Построение общей теории краевых задач для уравнений смешанного типа с произвольным многообразием изменения типа было начато в 70-е годы прошлого века В.Н. Враговым и рядом других авторов [1-4]. В дальнейшем эта. теория развивалась во многих направлениях [5-10]. При исследовании краевых задач для уравнений смешанного типа общего вида, применялись функциональные методы, метод регуляризации, метод Галеркина. Теория таких уравнений имеет важное значение при решении задач, возникающих в трансзвуковой газовой динамике [7] и во многих прикладных задачах механики.

В работе [11] стационарный метод Галеркина применяется к решению первой краевой задачи для уравнения смешанного типа, в работе [12] для этой задачи получена оценка погрешности стационарного метода. Галеркина через собственные числа оператора Лапласа по переменным x Е R n и t . В работе [13] к решению краевой задачи для уравнения смешанного типа в постановке В.Н. Врагова применен модифицированный метод Галеркина, и получена оценка его погрешности.

В настоящей работе рассматривается краевая задача, для уравнения смешанного типа второго порядка, которая в общем случае отличается от задач В.Н. Врагова [2,3] и А.Н. Терехова [4]. В случаях, когда, уравнение имеет эллиптический тип вблизи нижнего основания цилиндрической области, а. вблизи верхнего основания оно имеет эллиптический или гиперболический тип, с помощью модифицированного метода. Галеркина установлена, однозначная регулярная разрешимость краевой задачи в пространстве Соболева. Впервые постановка этой задачи была сформулирована авторами в работе [14], в которой ее разрешимость была исследована, для первого случая с помощью другой методики. В данной работе используется новый подход, который позволяет получить априорные оценки для приближенных решений сразу по всей области, на основании которых получена оценка погрешности модифицированного метода Галеркина.

1.    Постановка задачи

Пусть О С Rn - ограниченная односвязная область с гладкой границей S. Положим

Q = О х (0 ,T ) , St = S х (0 ,T ) , T = const >  0; О t = О х {t}, t G [0 ,T ] .

В цилиндрической области Q рассмотрим уравнение

Lu = k ( x, t ) u_tt — A u + a ( x, t ) ut + с ( x ) u = f ( x, t ) .                   (1)

Коэффициент k ( x, t ) может менять знак внутри области Q произвольным образом. Поэтому уравнение (1) является уравнением смешанного типа с произвольным многообразием изменения типа.

Предполагается, что коэффициенты уравнения (1) - гладкие функции. Введем множества

Р± = { ( x, 0) : x G О, k ( x, 0) > 0 }, P± = { ( x,T ) : x G О, k ( x,T ) > 0 }.

Краевая задача. Найти в области Q решение уравнения (1), такое, что u |sT = 0, u |р + = 0, Ut \t=0= 0, Ut |P- = 0.                        (2)

Отметим, что при k ( x, 0) >  0 задача (1), (2) совпадает с задачей Врагова [2, 3].

2.    Априорные оценки

Пусть CL есть множество гладких функций, удовлетворяющих условиям (2).

Лемма 1. Пусть коэффициент с ( x ) >  0 достаточно большой, и выполнены, условия:

k ( x, 0) <  0 , a — ^ kt > 5 >  0 .

Тогда существуют неотрицательные гладкие функции ф ( t ) , Д ( t ), такие, что для всех функций u G CL имеет место неравенство

( Lu, фu_t + Дu ) > C 1 || u^ 1; C 1 = const >  0 .

Доказательство. Найдется положительное число t0 < T, а также числа t1, t2 такие, что k(x,t) 6 —51 < 0, t G [0, t0], 0 < t2 < t1 < t0 < T.

Выбираем функции ф ( t ) , Д ( t ) G C^x [0 , T ] таким образом, чтобы

ф (0) = 0 , ф ( t ) > 0 , t G [0 ,t 2]; ф ( t ) 6 0 , t G [ 1 2 ,T ];

И.Е. Егоров, В.Е. Федоров, И.М. Тихонова

Ф ( t ) = e - ^{2 xt} , t E [ t 1 ,T ] , A> 0;

^ф ( t ) = ¹ + 2 ^ф ( t ) , t ^{E [0} ,t 2 ^]; ^ф ( t ) = ¹ - 2 ^ф ( t ) , t ^{E [} t 2 ,t i ^];

Ф ’ ( t ) 6 0 , t E [ t 1 ,T ]; ф ( t ) = 0 , t E [ t 0 ,T ] .

Для функций u E C L с помощью интегрирования по частям получим соотношение

( Lu, фu t +

Q

^— 2 ^k t ) ^{ф —} ( ^ф + 2 ^ф t ) к ^] u t +

+( ^{ф —} 2 Ф t ) ^ u X i + cu ²j + ^[ аф ^— ( ^кф ) t ^] u t u I dQ + I, (3)

где

I = ¹ e ^{2 XT}

n cu2 + 53 uXi I dx i=1

> 0 .

Теперь выберем A >  0 так, чтобы 6 + Ак >  6/ 2 . Тогда получим, что

( а — 2 k t ) ф — к ( ф + 2 ф t ) > min {6 1 , 2 6e ^{2 XT} }, ф — 2 ф t > min { 1 , Ae ^{2 XT} }.

Далее из соотношения (3), используя неравенство Коши и условия леммы, полу чаем утверждение леммы 1.

□

Для е >  0 поло жим L_eu = — ещц + Lu- В качестве базисных функций берем ф_к ( x ) , которые являются собственными функциями спектральной задачи

— А ф = Аф, x E fi , ф|₅ = 0 .

При этом функции ф_к ( x ) образуют ортонормированный базис в L ₂(П), а соответствующие собственные числа таковы, что 0 < А ₁ 6 А ₂ 6 ... и A k ^ + то пр и к ^ то.

В дальнейшем будем считать, что к ( x, 0) <  0. Приближен ное решение u ^N,e ( x,t ) краевой задачи (1), (2) ищем в виде

N uN,e (x,t) = v (x,t ) = ^ CN (t) фк (x), N > 1, E> 0, k=1

в котором c N^,e ( t ) определяются как решение следующей краевой задачи для системы обыкновенных дифференциальных уравнений третьего порядка:

(LeuN,e^i )0 = ( f,фl )0,(4)

DtcN,It=о = 0, DtcN^elt=o = 0, DtcNIt=t = 0, l = L,N,(5

при к ( x,T ) <  0 пли

DtcN£It=o = 0, DtcN^eIt=o = 0, Dtc^£It=t = 0, l = ДА,(5

при к ( x, T ) >  0 .

Лемма 2. Пусть выполнены условия леммы 1, f Е L ₂( Q ), и имеет место один из следующих случаев; либо k ( x,T ) <  0, либо k ( x,T ) >  0. Тогда существует число е 0 >  0, такое, что для приближенных решений краевой задачи (1), (2) справедлива оценка

е j TVttdQ + I I vH 1 6 C 2Il f I I² , C 2 >  0 , 0 < Е 6 е о •

Доказательство. Из (4) , (5 ¹ ) получаем соотношение

( f, Pvt + Vv ) = ^Е J VvttdQ - ^Е j

1(3 V + Ttt ) V2 + Vw dQ

Q L²

+ 2 е j ytvt dx + ( Lv, yvt + Vv ) •

Для функций v имеет место равенство (3). Достаточно рассмотреть k ( x,T ) >  5 ₂ >  0 . Выберем число е 0 >  0 так. что Хе 0 6 д ²- Тогда имеем

случай

I — ХЕе ^{2 XT} / vt dx >  0 .

Ω T

Теперь при необходимости уменьшая е 0, с учетом (3) из соотношения (7) получаем

априорную оценку (6).

D

Лемма 3. Пусть коэффициент c ( x ) >  0 достаточно большой, выполнены условия

a - 2 |kt| > ⁵> ^{0; f,f}t ^{Е L} 2⁽ Q ) ^,

и имеет место один из следующих случаев: либо k ( x, 0) <  0 , k ( x, T ) <  0, либо k ( x, 0) <  0 , k ( x,T ) >  0. Тогда сущеетвует число е 0 >  0, такое, что для приближенных решений краевой задачи (1),(2) справедлива оценка

Q v^tt + ^a ^ vta^ ^{dQ 6} C 3 [ ^{11 f 11 2} + llftll ²] ^, C 3 >  ^{0 , 0} < ^{Е 6 Е} 0 ^{,         (8)}

где a = 1 щш k ( x,T ) <  0 t1 a = 0 ny m k ( x,T ) >  0.

Доказательство. Для неотрицательных бесконечно дифференцируемых функций б, п из (4) , (5 ¹ ) получаем соотношение

^{— ( f, 6}vttt + nvtt ) = ^ЕI ^{6 (} vttt ⁾² d^{Q —}

2 ^Е

j nt^v2t^dQ +

+

⁺ 2 kt ) ^{6 — k (} п ^— 2 ) vtt + ⁽ п

n

— ₂ 6t ) ]=1 ( vtx, П dQ

+ j [⁽ a⁶ ) t + c^{6 —} aⁿ ] vttvtdQ + j ⁽ c^t ^— cⁿ ) ^vtt^vdQ + j ^{( n}t ^— 6tt ) ^^ ^vtx_t vxt^dQ + J ⁽⁹⁾

И.Е. Егоров, В.Е. Федоров, И.М. Тихонова где

J = X 2 ^{( е}п - k^ ) v2 -

+ A v ( (v tt — ( t v t ) - c(vv tt

n aCvttvt + 1 ( E vx + i=1

n

- η    vxivtxi i=1

dx| ^tt ⁼=0 ^T

Сначала рассмотрим случай, когда k(x, 0) < 0, k(x,T) < 0. Тогда найдется положительное число Tо < T такое, что k(x, t) < —5i < 0, T0 < t < T.

Выберем функции ( ( t ) , n ( t ) такие, что

С ( t ) = ц >  0 , 0 < t < T _D;

( ( T ) = 0; ( ( t ) 6 0 , T о < t < T ;

П ⁽ t ) = ¹ •

Теперь выберем число ц >  0 так, чтобы

5ц — max \k\ > 5 2 >  0 •

Q

Тогда будем иметь

A = ( a + 2 k t ) С — k ( П — 2 ( t ) > min {5 i , 5 2 }•

В силу условий (5¹) получаем. что J = 2 е J v tt dx неотрицательна.

Ω T

Применяя неравенство Коши в подчиненных членах равенства (9), получим априорную оценку (8) при а = 1.

Теперь рассмотрим случай, когда k ( x, 0) <  0 , k ( x, T ) >  0. Пусть ( ( t ) = 1 , n ( t ) = 0. Тогда с учетом условий леммы и (52) получаем, что

1 Г n

J = ^   v x dX^dx > ⁰ , A >  ⁵.

_{Ω T} i =1

Применяя неравенство Коши в подчиненных членах равенства (9), получим априорную оценку (8) при а = 0.                                                   □

Лемма 4. Пусть выполнены все условия леммы 3. Тогда сухцествует число е о >  0, такое, что для приблиснсенных решений краевой задачи (1),(2) справедлива оценка

У a v\\ ² 6 C 4( у у ² + у\\ ²) , C 4 >  0 , 0 <е 6 е о .                 (10)

Доказательство. Для неотрицательных гладких функций ( ( t ) , n ( t ) ^из (4) получаем соотношение

— ( f,( A v t + n A v ) = е

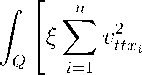
- n

₂( ( tt + 3 n t )E i =1

v

tx i

-

η tt

n vxivtxi i=1

dQ +

где

+ / (( п - 2 C t ) (A v )² +^[ a^c - Q

nn

2(kc) t] Е v2xi + cvtt Е kxi vtxi+ i=1             i=1

nnn

+vtC E axi VtXi + Cc E VtXi Vxi + Cv E Cxi VtXi i=1               i=1               i=1

-

П ( kv_tt + av t + cv

^)A v}

dQ + K,

(П)

K≡ _Ω

nn

1 ^{Е ( c} t + п ) E v X + ^ЕУп ^A v t + ^En t E v tx i v x i + i =1                           i =1

n

+envttAv + 1 c(Дv)2 + 1 kc £ v2x i=1

dx| ^tt ⁼ =0 ^T

При k ( x, 0) <  0 , k ( x,T ) <  0 предполагаем, что C ( t ) = Ф ( t ) , П ( t ) = Ф ( t ) , ^гД^е

функции ф, ф построены в ходе доказательства леммы 1. С учетом условий леммы

и (51) получаем, что

K =

_e - 2 λT

j T ⁽A v )

² dx >  0 .

Теперь с учетом теоремы о следах для f ( x,T ) и выражения для K , неравенства (6), оценки (8) при ст = 1 из соотношения (11) получим оценку (10).

В случае k ( x, 0) <  0 , k ( x, T ) >  0 достаточпс) положить C ( t ) = 0 , п ( t ) = 1- С учетом условия (5²) соотношение (11) принимает вид

- ( f, A v )= [ [(A v )² - ( kv tt + av t + cv )A v ] dQ + | e / ^ v tx i dx.

Q                                       ^{2 Q} t i =1

Из последнего соотношения, используя неравенство Коши и оценки (6), ст = 0, получаем априорную оценку (10).

(8) при □

3.    Разрешимость и оценка погрешности

Теорема 1. Пусть коэффициент c(x) > 0 достаточно большой, выполнены, условия a — ^|kt| > 5 > 0, f, ft с L2(Q), и имеет место один из следующих случаев; либо k(x, 0) < 0, k(x, T) < 0, либо k(x, 0) < 0, k(x,T) > 0. Тогда краевая задача (1), (2) имеет единственное решение u(x, t) из W2(Q), и справедлива оценка

^и^ 2 6 C 5 ( У У + У У ) , C 5 >  0 .

Доказательство. Из неравенств (6), (8), (10) и второго основного неравенства для оператора Лапласа для приближенных решений краевой задачи (1), (2) имеет место оценка

\\uN’^£\\ 2 6 C 5( У У + У\\ ) , 0 <Е 6 Е 0 . (12)

В силу оценки (12) стандартным образом доказывается существование искомого решения краевой задачи (1), (2), а его единственность следует из леммы 1.       □

И.Е. Егоров, В.Е. Федоров, И.М. Тихонова

Теорема 2. Пусть выполнены все условия теоремы 1. Тогда для погрешности модифицированного метода Галеркина справедлива оценка

где а ( x, t ) - точное решение краевой задачи (1), (2).

Доказательство. Рассмотрим функции C ( t ) = ф ( t ) , п ( t ) = Ф ( t ) , построенные в ходе доказательства леммы 1. В пространстве L ₂( Q ) введем линейное многообразие

N

Hn = {7 ( x,t ) = ^ d i ( t ) Ф 1 ( x ): d i G W2(0,T ) , dl (0) = d i ( T )=0 , l = LN}, l =1

при k ( x,T ) <  0. пли

N

Hn = {7(x,t) = ^di(t)Ф1 (x): di G W2(0,T), dl(0) = 0, l = 1N}, l=1

при k ( x, T ) >  0.

Из равенств (4) путем арифметических действий легко получить соотношение

⁽ L e «^N'^e,^7 t + П7 ) = ^{( f,}^7 t + П7 ) ^, ^7 ^G H N ■

Кроме того. ( Па, <7 t + п7 ) = ( f, C7 t + П7 ) , ^7 G Hn ■

Из этих равенств получаем:

⁽ L ⁽ « - u ^N,£ ) ,<7 t + п7 ) = ^{- ( Еа}ш\^ + П7 ) ^, ^7 ^G H N ■

Для любой функциии ш из H_N поло жим 7 = ш — uⁿ'' . Тогда

У L ( а — u ^N,' )[ C ( « t

— u N' ) + п ( а — uⁿ’' )] dQ

= Е [ а^ [ £ ( Ш tt

Q

^{— u} N’' ) + ^{п ( w} t ^{— u} N'' ) + C t ^{( ш} t ^{— u} N'' ) + ⁿ t ⁽ « ^{— ш )]} d^Q +

+

I.(f

— Lu^N'^e )[ C ( u t — W t ) + п ( а — ш )] dQ.

В силу теоремы 1 W ₂²( Q ). такое. что а = оценки

краевая задача (1), (2) имеет единственное решение а ( x,t ) из ∞∞

Ckфк- аt G W1(Q). аt = X c'kФк- Ck = (а,Фк)о- п справедливы k=1

∞T

■£ Лк У0 |ck (t )12 dt = Уек=1 (а»к)2 dQ 6 C7( Bf,B2 + Bf В 2) ,с7 > 0.(15)

N

При W = х C k ( t ) ф к ( x ) имеем:

k =1

∞

|u t Ω

∞

= Е I ck (t) ।2 ■ k=N+1

^{— W} t ^{1 2 dx} = I I ^ c k ⁽ t ) Ф к I I ²

k = N +1

Тогда

∞T                ∞ llut - w^2 = E J^ c(t)|2dt 6 ^—- E Хк у0 c(t)|2dt.(16)

Аналогично справедлива оценка

∞T

Е Ak /0 |ck(t)12dt = /V(Uxk)2dQ 6 C8If ||2, C8 > 0,(17)

а также равенство

I J u

- ω| dx

∞ n E ck (t) Фк 10

k = N +1

∞

E ।c k ( t ) i ² .

к = N +1

Тогда

∞ _T                 ∞       _T

||u - Ml² = E J c k ( t ) I ² dt 6 ~ E A k J Ic k ( t ) | ² dt.

Используя лемму 1, с учетом неравенств (15) - (18) из равенства (14) получаем оценку (13) погрешности модифицированного метода Галеркина.                □

Замечание 1. Краевая задача (1), (2) при k ( х, 0) >  0 , k ( x,T ) > 0 и k ( х, 0) >  0 , k ( x,T ) <  0 совпадает с краевой задачей В.Н. Врагова. Следовательно, для краевой задачи (1), (2) в этих случаях справедливы аналогичные результаты [13].

Работа виполнена в рамках Государственного задания Минобрнауки России на 2014^2016 годи (проект №3041).