Модифицированный метод выделения. О границах корректного применения

Модифицированный метод выделения (далее – ММВ), предложенный 15 лет назад для оценки незастроенных земельных участков (см. [1]), в последнее десятилетие активно развивается (см. [2–10]). Преимуществом этого метода является, как справедливо отмечается в ряде публикаций, возможность привлечения дополнительной рыночной информации к оценке свободных или условно свободных земельных участков и повышения на этой основе надежности их оценок. Последние публикации, например [10], посвящены исследованиям «тонких» свойств ММВ и свидетельствуют о достаточно глубоком анализе практики его применения.

Модифицированный метод выделения, как и его предшественник, по сути, основан на декомпозиции стоимости единого объекта недвижимости на стоимость земельного участка (далее также – ЗУ) и стоимость улучшений [4]. При этом очень важна корректность этой декомпозиции: как стоимость земельного участка, так и стоимость улучшений должны быть рыночными, то есть обладать всеми атрибутами рыночной стоимости, включая соответствие наиболее эффективному использованию (далее – НЭИ) оцениваемой составляющей объекта недвижимости. Таким образом, предлагаемый подход, как и его предшественник, может дать хорошие результаты только для сравнительно новых объектов недвижимости, использование которых соответствует НЭИ земельного участка (см. [11, с. 59]). Использование в качестве аналогов единых объектов недвижимости, НЭИ земельных участков которых отличается от НЭИ оцениваемого участка, без соответствующей корректировки стоимости их улучшений на использование приведет к нерыночным результатам оценки. Это недопустимо для индивидуальной оценки рыночной стоимости ЗУ, на которую претендует предлагаемый метод.

Это означает, что в качестве аналогов для применения ММВ должны отбираться объекты недвижимости, наиболее эффективное использование которых совпадает с НЭИ их земельных участков как незастроенных (условно свободных). Только в этом случае выделение стоимости земельного участка из стоимости всего объекта недвижимости позволяет получить рыночную стоимость ЗУ.

Кроме того, как показывает анализ, ММВ часто применяется без учета ограничивающих допущений, сформулированных в публикациях [1], которую можно считать постановочной для ММВ, и [4]. Выход за пределы этих ограничений может приводить к нежелательным последствиям – существенному смещению оценок удельной стоимости земельного участка и улучшений. Покажем это.

Напомним основные соотношения ММВ для стоимости объекта.

В основе метода лежит представление стоимости объекта недвижимости (далее также – ОН) как суммы стоимостей земельного участка (ЗУ) и его капитальных улучшений (УЛ):

V_он = V_зу + V_ул = v_зуS_зу + v_улS_ул , где v_зу , v_ул – удельные стоимости ЗУ и улучшений; S_зу , S_ул – площади ЗУ и улучшений.

Разделив правую и левую части уравнения (1) на конечную площадь земельного участка, получим выражение для приведенной стоимости объекта недвижимости:

v_он = v_зу + v_улk_пз ,                                                                                         (2)

где v_он = V_он / S_зу – стоимость ОН, приведенная к единице площади ЗУ;

k_пз = S_ул / S_зу – коэффициент плотности застройки (см. [1]).

Построение уравнений (1) и (2) не вызывает никаких возражений или вопросов. Но эти уравнения не имеют практической ценности для использования в качестве расчетного инструмента для оценки стоимости. Такой инструмент появляется при представлении уравнения (2) в виде однофакторной линейной регрессионной зависимости приведенной стоимости объекта недвижимости v_он от коэффициента плотности застройки земельного участка k : пз

~ _ _ - - y = a ₀ + a ₁ x , где yˆ = v_он ;

a ₀ = v_зу ;

a ₁ = v_ул; x = k_пз .

При этом предполагается, что все остальные ценообразующие факторы не влияют на оценку стоимости.

Уравнение (3) представлено в терминах стоимости. Однако на рынке мы имеем дело не со стоимостями, а с ценами объектов-аналогов, по выборке которых строится регрессионная модель посредством определения значений постоянных коэффициентов а ₀ = v_зу и а ₁ = v_ул .

Система линейных уравнений для выборки, например, из пяти аналогов выглядит следующим образом:

у 1 = a 0 + a 1 x 1 + £ 1

у 2 = a 0 + a 1 x 2 + £ 2

y, = a + ax + £ 50155

Здесь значения зависимой переменной y представляют собой приведенные к единице площади земли цены аналогов объектов недвижимости, значения случайных остатков ɛ характеризуют отклонения цен аналогов от линии регрессии, то есть от линейной связи приведенной стоимости объекта недвижимости с плотностью застройки земельного участка. Наглядно видно, что для всех объектов-аналогов значения коэффициентов а ₀ = v_зу и а ₁ = v_ул являются одними и теми же . Об этом же условии применения метода пишется в публикации [4]: «Таким образом, если у оценщика, исследовавшего объект оценки и объекты, используемые в качестве аналогов, есть основания считать, что объекты-аналоги и объект оценки имеют одинаковые (хотя и неизвестные) удельные стоимости земельных участков и улучшений ( ρ _i = ρ ₀ и c_i = c ₀), то … можно записать …: V_i / S_i = ρ ₀ + c ₀ Q_i / S_i + ξ _i , где

ρ ₀ – неизвестная удельная стоимость оцениваемого земельного участка; c ₀ – неизвестная удельная стоимость улучшений, входящих в состав единых объектов недвижимости, используемых в качестве объектов-аналогов».

Значения коэффициентов уравнения регрессии (3), полученные посредством решения системы линейных уравнений (4), представляют собой оценки удельных стоимостей земельного участка и улучшений в предположении об их стабильности для всех объектов сравнения – аналогов и объекта оценки.

Отличительной особенностью ММВ как регрессионной модели является то, что коэффициенты а ₀, а ₁ уравнения (3) не являются простыми константами, как это принято в «классических» регрессионных моделях, а представляют собой экономические величины, подчиняющиеся рыночным закономерностям. Широко известно (см., например, [12]), что удельная цена земельного участка не остается постоянной с изменением площади участка (фактор масштаба) при прочих равных условиях. Удельная цена улучшений (объектов капитального строительства; далее также – ОКС) также не остается постоянной с изменением масштаба строительства. Об этом свидетельствует, например, поправка к стоимости строительства на разницу в объеме или площади объекта оценки и аналога (см. [13]).

Если изменения удельных цен земли и улучшений с изменением масштаба являются заметными, то в регрессии появляются дополнительные влияющие факторы. Без потери общности можно представить изменяющиеся значения каждой из удельных стоимостей в виде суммы постоянной составляющей и некоторой функции от соответствующей площади:

а 0 = v зу = а 0 const + а 0 var f 2 ( S зу );

а1 = vул = а1 const + а1 varf3(Sул).(5)

Подставляя (5) в уравнение (3) и проводя простейшие преобразования, получаем:

yˆ = а0 const + а1 constx + а0 varf2(Sзу) + а1 varf3(Sул)x.(6)

Заменяя обозначения постоянных коэффициентов регрессии при влияющих факторах, запишем уравнение (6) в более традиционном виде 1:

yˆ = b0 +b1 x + b2f2(Sзу) + b3f3(Sул)x.(6

Как следует из выражения (6 ' ), однофакторная регрессия ММВ, которую представляют два первых слагаемых выражения, в случае заметных изменений удельных цен земли и улучшений превращается в трехфакторную ². Кроме плотности застройки ( х = k_пз ), влияющими факторами становятся площади земли S_зу и улучшений S_ул .

Использование в этих условиях однофакторной модели означает пропуск (невключение в модель) других существенно влияющих факторов. Теория и практика регрессионного анализа (см., например, [15, 16]) относят такой пропуск влияющих факторов к грубым ошибкам спецификации регрессионной модели. Подобные ошибки приводят к неконтролируемому смещению регрессионных оценок коэффициентов уравнения и зависимой величины.

ММВ, как разновидность метода регрессионного анализа, является методом количественной оценки, поэтому важнейшим условием корректного его применения является получение несмещенных оценок стоимости земельного участка (и/или улучшений). На это указывается и авторами ММВ как в постановочной [1], так и в более поздних [4, 10] публикациях.

Отсюда вытекает задача контроля возможных изменений удельных цен (коэффициентов уравнения) при изменении площадей земельных участков и их улучшений в пределах выборки объектов-аналогов. Оценка таких изменений необходима для их ограничения с целью предотвращения смещения оценок регрессионных коэффициентов в уравнении ММВ.

Рассмотрим на простом примере влияние изменения удельных цен на оценки коэффициентов однофакторной регрессионной модели. Для этого сначала построим идеализированную модель с постоянными удельными ценами и отсутствием субъектной составляющей в ценах на выборке из пяти объектов-аналогов (см. табл. 1).

Таблица 1

Характеристики аналогов в «идеализированной» модели ММВ

Аналог	Площадь участка (Sзу), кв. м	Площадь улучшений (Sул), кв. м	Плотность застройки (k пз )	Удельная цена земли (vзу), р. / кв. м	Удельная цена улучшений, (vул), р. / кв. м	Приведенная удельная цена объекта (VOH = v3y + v^n X кпз ), р. / кв. м
1	2 500	850	0,34	10 000	60 000	30 400
2		1 675	0,67	10 000	60 000	50 200
3		2 500	1,00	10 000	60 000	70 000
4		3 200	1,28	10 000	60 000	86 800
5		4 500	1,80	10 000	60 000	118 000

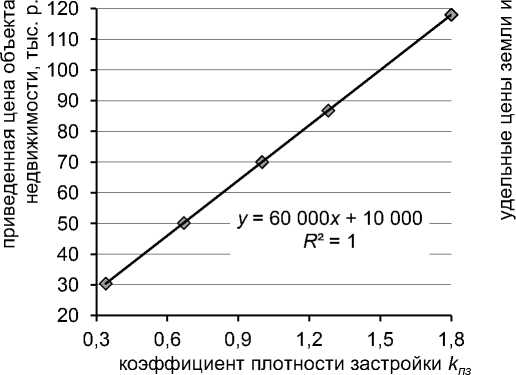
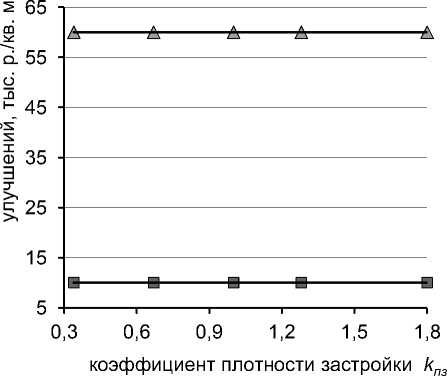
Графики уравнения ММВ yˆ = a ₀ + a ₁ x , а также зависимости коэффициентов уравнения a ₀, a ₁ от плотности застройки, полученные по выборке, представлены на рисунке 1.

а)                                                       б)

Рис. 1. Зависимости в идеализированной модели ММВ: а) приведенной цены объекта недвижимости V_он / S_зу и б) удельных цен земли а ₀ и улучшений a ₁ от плотности застройки k_пз

Обратим внимание на то, что все точки уравнения ММВ лежат строго на прямой, а коэффициенты a ₀, a ₁ равны заданным в примере удельным ценам земли и улучшений соответственно. Отметим также, что в идеализированном случае нет никакой зависимости удельных цен от плотности застройки, как нет и зависимости удельной цены улучшений от площади улучшений v_ул = f( S_ул ) = const и удельной цены земли от площади земельного участка v_зу = f( S_зу ) = const (см. табл.1).

Теперь рассмотрим данные справочника КО-ИНВЕСТ [12] о зависимости поправки к удельным затратам на создание (стоимость строительства) ОКС от соотношения площадей объекта S_o и аналога S_a (см. табл. 2, рис. 2).

Таблица 2

Значение поправочного коэффициента на разницу в площадях объекта оценки и аналога

Отношение площадей S o / S a	Середина интервала	Поправочный коэффициент (k s )
0,25–0,49	0,34	1,20
0,50–0,85	0,67	1,10
0,86–1,15	1,00	1,00
1,16–1,50	1,28	0,95
1,60–2,00	1,80	0,93

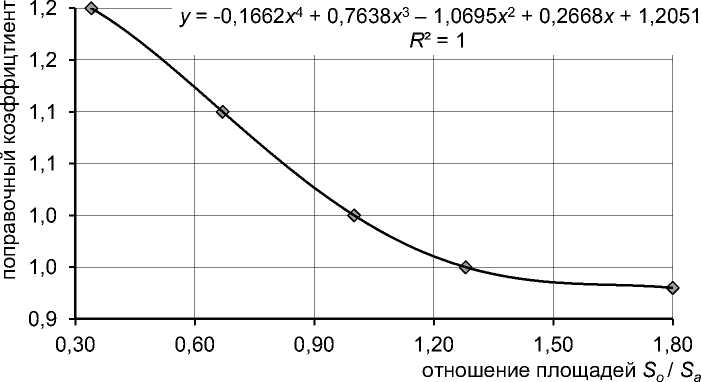
Рис. 2. Зависимость поправочного коэффициента k_s к справочным удельным затратам на строительство от соотношения площадей S_o / S_a объекта оценки и справочного аналога

Допустим, что стоимости улучшений подчиняются зависимости, указанной в справочнике. Не настаивая именно на таком характере зависимости 3, отметим относительно небольшое снижение удельной цены улучшений (примерно на 23 процента) при существенном (более чем в 5 раз) изменении площади объекта капитального строительства. То есть следует признать относительно слабым влияние масштаба на удельную стоимость строительства. Тем более интересной является оценка влияния этого относительно слабого изменения удельной цены на результаты, получаемые с помощью ММВ.

Не меняя никаких других условий, учтем в ценах аналогов выявленную зависимость поправочного коэффициента к удельной цене улучшений по формуле v_oH кор = v_3y + v_oH х k s х к пз .

В качестве базового объекта для удобства выбреем аналог 3 с площадью улучшений 2 500 квадратных метров (см. табл. 3).

Таблица 3

Учет поправочного коэффициента на разницу в площади улучшений

Аналог	Площадь улучшений (Sул), кв. м	Плотность застройки (k пз )	Поправочный коэффициент (k s )	Скорректированная цена ОКС, р. / кв. м
				удельная (v ул кор )	приведенная (v он кор )
1	850	0,34	1,20	72 000	34 480
2	1 675	0,67	1,10	66 000	54 220
3	2 500	1,00	1,00	60 000	70 000
4	3 200	1,28	0,95	57 000	82 960
5	4 500	1,80	0,93	55 800	110 440

Отметим появление разброса удельных цен ОКС v_{ул кор} = 55 800 – 72 000 р./кв. м при среднем значении 62 160 р./кв. м.

Теперь построим для этой приближенной к реальности модели зависимость скорректированной приведенной стоимости объекта недвижимости v_{он кор} от коэффициента плотности застройки k_пз (рис. 3).

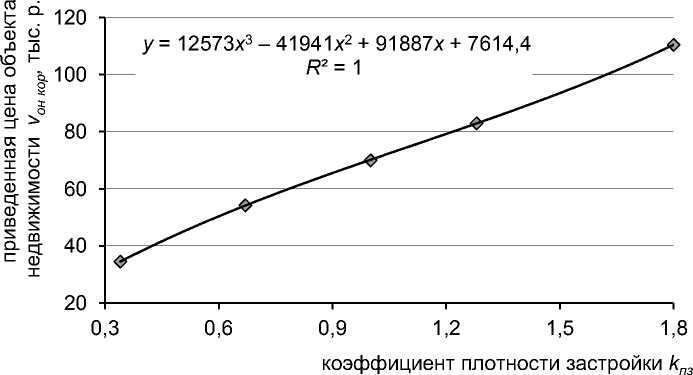
Рис. 3. Реалистичная нелинейная зависимость v_{он кор} = f( k_пз )

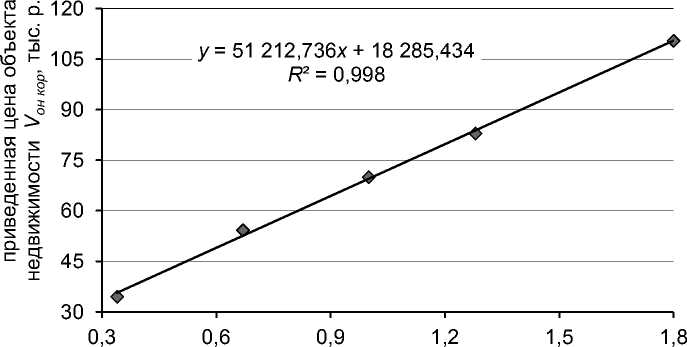
Как видим, реалистичная зависимость приведенной цены объекта недвижимости не является линейной (как в идеализированной модели, представленной на рисунке 1), хотя по виду весьма близка к ней 4. Построим линейную аппроксимацию этой реалистичной зависимости (рис. 4).

коэффициент плотности застройки к _пз

Рис. 4. Линейная аппроксимация v_{он кор} = f( k_пз ) = а ₀ + а ₁ k_пз реалистичной нелинейной зависимости

Линейная аппроксимация нелинейной зависимости обладает великолепными показателями воспроизведения исходных данных о приведенных ценах единого объекта v_{он кор} : коэффициент детерминации R ² = 0,998, средняя ошибка аппроксимации СОА = 1,7%, максимальная ошибка не превышает 3,5 процента ⁵. То есть по этим показателям нет никаких оснований сомневаться в линейном характере реальной зависимости цен объектов недвижимости от плотности застройки земельного участка.

Но взглянем на оценки коэффициентов модели ММВ, полученные при этой весьма точной аппроксимации. Свободный член уравнения, характеризующий удельную стоимость земли, оценивается в размере a ₀ = v_зу = 18 285 р./кв. м, что в 1,8 раза (!) превышает заданное по условиям примера значение – 10 000 р./кв. м. То есть оценка удельной стоимости земли оказалась остро чувствительной к отклонению уравнения ММВ от линейной зависимости, обусловленному непостоянством удельных цен улучшений.

Оценка удельной стоимости улучшений также смещена, хотя и в значительно меньшей степени: a ₁ = v_ул = 51 213 р./кв. м, что почти на 15 процентов меньше заданной в идеализированной модели ⁶.

Что же является причиной столь существенного смещения оценок стоимости земельного участка и улучшений в ММВ с уравнением, статистически точно описывающим приведенные цены единых объектов недвижимости? Как мы уже показали, единственной причиной явились различные значения удельной цены улучшений аналогов выборки, оцениваемые одним значением коэффициента a ₁ в системе уравнений (4). Причем вариацию удельных цен нельзя назвать значительной ⁷ – крайние значения отличаются на минус 7 процентов и плюс 20 процентов от «базового» значения 60 000 р./кв. м или минус 10 процентов и плюс 11,5 процента относительно среднего значения.

Еще раз обратим внимание на то, что значения коэффициента детерминации и средней ошибка аппроксимации, которые используются как показатели «точности» уравнения ММВ, свидетельствуют о высоких прогнозных свойствах модели в отношении приведен- ных цен единых объектов недвижимости. Но эти показатели не свидетельствуют о наличии нарушения предпосылки ММВ о постоянстве удельных цен улучшений для всех аналогов. Другими словами, обеспечивая высокую точность оценки стоимости единого объекта недвижимости 8, метод может одновременно давать существенно смещенные оценки ее составляющих, прежде всего стоимости земельного участка.

Но если используемые на практике показатели «точности» уравнения ММВ не способны индицировать приводящие к смещенным оценкам отклонения реальных данных от допущения ММВ о постоянстве удельных цен, нужны дополнительные показатели, способные на это.

Построим графики зависимости удельной цены улучшений (коэффициента a ₁) от плотности застройки земельного участка k_пз по исходным данным (табл. 3) и уравнению ММВ (см. табл. 4, рис. 5).

Таблица 4

Значения удельных цен улучшений аналогов и плотности застройки

Удельная цена a1 = Vул / Sул, р./кв. м		Плотность застройки (k пз = S ул / S зу )	Площадь улучшений (Sул), кв. м
по данным табл. 3	по уравнению ММВ
72 000	35 631	0,34	850
66 000	47 634	0,67	1 675
60 000	51 715	1,00	2 500
57 000	53 527	1,28	3 200
55 800	55 397	1,80	4 500
а 1 макс / а 1 мин = 1,29	а 1 макс / а 1 мин = 1,55	–	–

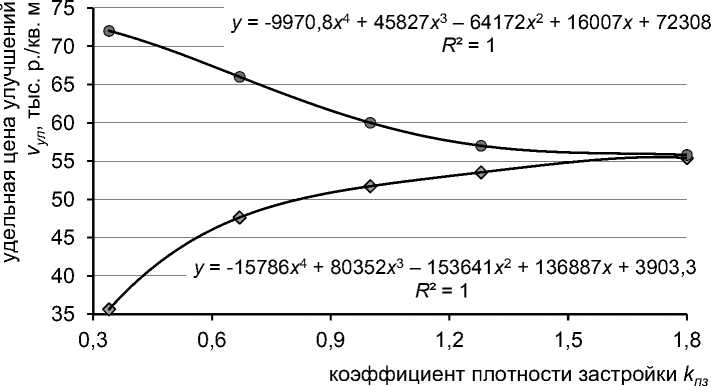
Рис. 5. Зависимости удельной цены улучшений a ₁ = v_ул = f( k_пз ) от плотности застройки земельного участка по данным таблицы 3 (круги) и аппроксимирующему уравнению ММВ (ромбы)

Алгоритм расчета значений удельной цены улучшений для каждого из аналогов по уравнению ММВ включает три шага:

• 1)    рассчитывается стоимость земельного участка, одинакового для всех объектов сравнения: V_3y = а 0 х S_3y как произведение оценки удельной стоимости а 0 = 18 285,43 р./кв. м и площади участка S_3y = 2 500 кв. м, V_3y = 18 285,43 х 2 500 = 45 713 586 р.;

• 2)    из скорректированной цены каждого аналога вычитается стоимость V_зу = 45 713 586 р., полученная на шаге 1; результатом является цена улучшений V_ул = V_он – V_зу каждого аналога;

• 3)    полученная на шаге 2 цена улучшений V_ул каждого аналога делится на площадь его улучшений, результатом является удельная цена улучшений v_ул = V_ул / S_ул.

Помня, что в рассмотренном примере площадь земельных участков у всех аналогов одинаковая и плотность застройки является отношением площадей улучшений и земельного участка, легко убедиться, что зависимости от площади улучшений a ₁ = f( S_ул ) имеют тот же вид (с точностью до единиц оси х ).

Как уже отмечалось, оценка удельной стоимости земли в аппроксимирующей линейной модели существенно завышена. Это привело к смене направления изменения удельной цены улучшений – вместо убывающей с увеличением площади (см. табл. 3) она стала возрастающей. Однако важным остается их общее свойство – отражение непостоянства удельной цены улучшений по выборке аналогов . Важно это потому, что в отличие от рассмотренного нами идеализированного примера на практике объекты сравнения отличаются площадями не только улучшений, но и земельных участков. В таких условиях не видно иной возможности проверить постоянство коэффициентов регрессионного уравнения ММВ иначе как вычислением значений одного из коэффициентов в предположении о постоянстве другого, и наоборот.

Теперь рассмотрим два примера применения ММВ в практике оценки по данным публикаций [7 и 9]. Напомним, что использование ММВ в реальных условиях осложняется не только различиями аналогов по площади земельных участков, но и наличием субъектной составляющей в ценах аналогов, мешающей выявлению реальных зависимостей.

В публикации [7] цены аналогов не подвергались корректировкам на различия в свойствах объектов исходя из предположения об отсутствии существенных различий по ценообразующим факторам (табл. 5), уравнение ММВ строилось по нескорректированным ценам (рис. 6).

Таблица 5

Характеристики аналогов при применении ММВ для оценки коттеджного домовладения [7] *

Площадь, кв. м		Плотность застройки ЗУ (kпз)	Цена объекта недвижимости (Vон), тыс. р.	Приведенная цена ОН (V он / S зу ), тыс. р./кв. м
земельного участка (S зу )	коттеджа (S ул )
1 220	180	0,148	20 400	16,72
1 336	220	0,165	21 900	16,39
1 252	220	0,176	21 400	17,09
1 000	180	0,180	19 500	19,50
1 408	220	0,156	21 900	15,55
1 383	180	0,130	21 400	15,47
1 264	180	0,142	20 900	16,53

Окончание таблицы 5

1 220	180	0,148	17 900	14,67
1 600	550	0,344	39 900	24,94

* В таблице использованы обозначения величин, принятые в настоящей статье.

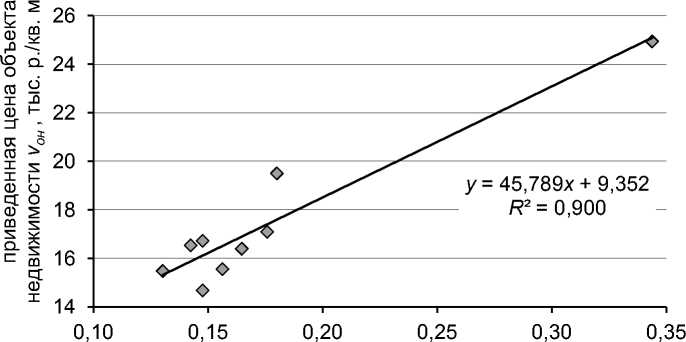
коэффициент плотности застройки к _пз

Рис. 6. Зависимость приведенной стоимости объекта недвижимости y = V_он / S_зу от плотности застройки x = k пз

Анализ данных, использованных для построения модели ММВ, показывает, что выборку аналогов можно признать однородной по площади земельных участков ( S_{зу макс} / S_{зу мин} = 1,6), и неоднородной по площади коттеджей ( S_{зу макс} / S_{зу мин} = 3,1) ⁹. Тем не менее показатели «точности» модели достаточно хороши (коэффициент детерминации R ² = 0,9, средняя ошибка аппроксимации СОА = 4,9%, максимальная ошибка не превышает 9,8 процента) ¹⁰.

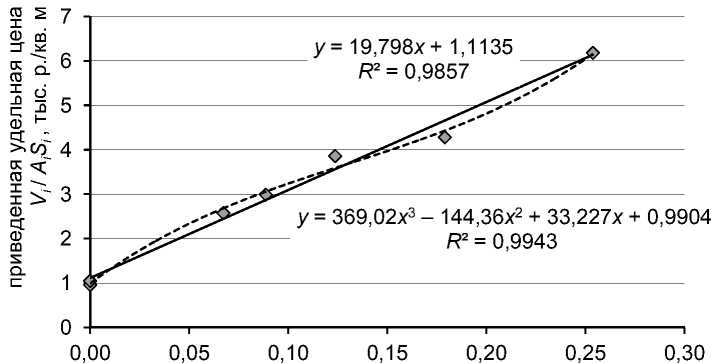
Попытаемся проверить постоянство коэффициентов регрессионного уравнения. Для этого предположим, что удельная цена земли постоянна и оценена верно: v ₀ = a ₀ = const = 9 352 р./кв. м. На ее основе рассчитаем для каждого аналога стоимость земельного участка V_зу и, вычитая полученную стоимость участка из цены объекта V_он , найдем цену коттеджа V_ул . Разделив цену коттеджа на его площадь, получим удельную цену коттеджа v_ул , зависимости которой от площади коттеджа и плотности застройки нас интересуют (см. рис. 7).

Характер зависимостей a₁ = v_ул от площади коттеджа и плотности застройки ожидаемо достаточно близки в силу однородности выборки аналогов по площади земельного участка (см. выше). Обе зависимости не имеют выраженных трендов, но разброс значений удельной цены v_{ул макс} / v_{ул мин} = 1,56 значителен и вряд ли может быть объяснен только наличием субъектной составляющей в ценах объектов-аналогов. Величина разброса 1,56 практически совпадает с величиной разброса 1,55, рассчитанной по уравнению аппроксимации в «приближенном к реальности» примере (см. табл. 4), в котором получены смещенные оценки удельных стоимостей улучшений и особенно земельного участка.

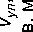
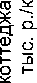
о

о

R ² = 0,0098

150 200 250 300 350 400 450 500 550

0,10   0,15   0,20   0,25   0,30   0,35

площадь коттеджа S_yn

коэффициент плотности застройки к_пз

а)                                                      б)

Рис. 7. Зависимость коэффициента уравнения a ₁ = v_ул = V_ул / S_ул : а) от площади улучшений S_ул , б) от плотности застройки k_пз

Есть все основания полагать, что и в рассматриваемом примере применения ММВ оценка удельной стоимости земли также существенно смещена. В пользу этого говорит и доля земельного участка в цене объекта недвижимости, среднее значение которой по всем аналогам составляет 55 процентов, а без аналога с коттеджем площадью 550 квадратных метров – 57 процентов. Дополнительным аргументом служит заметное изменение оценок удельных стоимостей при удалении из выборки одного из аналогов (см. сноску 9).

В другом примере реализации ММВ [9] представлена комбинация метода количественных корректировок и ММВ согласно методологии, описанной в работе [4]. Цены аналогов и ряд показателей перед определением зависимости от плотности застройки подвергнуты десяти (!) корректировкам, призванным нивелировать влияние всех иных факторов (табл. 6), в результате получена искомая регрессионная зависимость (см. рис. 8).

Таблица 6

Скорректированные характеристики аналогов при применении ММВ для оценки производственно-складского объекта [9] *

Аналог	Приведенная площадь, кв. м		Приведенная плотность застройки k qs = Q i B i / A i S i	Приведенная удельная цена (Vi / AiSi), тыс. р./кв. м
	земельного участка (A i S i )	строений (Q i B i )
1	26 536,14	6 732,00	0,2537	6,18025
2	17 550,00	2 169,97	0,1237	3,85937
3	18 094,00	1 605,18	0,0887	2,9910
4	20 680, 00	1 390, 80	0,0673	2,57737
5	22 990,00	4 116,00	0,1790	4,28012
6	7 520,70	0	0,0	0,95949
7	15 150,00	0	0,0	1,05003

* В таблице сохранены обозначения публикации [9].

приведенная плотность застройки Q i B i / A i S i

Рис. 8. Зависимости приведенной удельной цены объекта недвижимости y = V_i / A_iS_i от приведенной плотности застройки x = Q_iB_i / A_iS_i (нелинейная аппроксимация – полином третьей степени и линейная аппроксимация)

Большое число корректировок при точном их введении дает основание предполагать отсутствие влияния каких-либо иных факторов, кроме плотности застройки, в том числе отсутствие влияния фактора масштаба на удельные цены земли и улучшений. То есть мы вправе ожидать стабильности удельных цен и точности их отражения коэффициентами уравнения ММВ в преобразованных координатах.

Традиционные показатели «точности» линейной аппроксимации вполне приемлемы: средняя ошибка аппроксимации СОА = 6,9% при максимальной ошибке около 16 процентов, значение коэффициента детерминации R ² = 0,985 весьма высоко. Хотя гораздо более точное приближение к реальной зависимости достигается полиномом третьей степени (рис. 8, пунктирная кривая), как и в реалистичном примере (см. рис. 3 и 4), в котором оценки коэффициентов были существенно смещены.

Но как обстоит дело с постоянством удельных цен, описываемых коэффициентами регрессионных моделей? В отличие от рассмотренных ранее примеров в использованной выборке аналогов площади земельных участков заметно различаются ( S_{зу макс} / S_{зу мин} = 2,9), различия площадей улучшений застроенных участков ( S_{ул макс} / S_{ул мин} = 3,7) также превышают аналогичные различия в предыдущем примере, в котором были использованы данные работы [7].

В связи с этим нет оснований предполагать относительное постоянство одного из коэффициентов уравнения, как это было в предыдущем примере, и необходимо последовательно рассмотреть зависимости обоих коэффициентов от соответствующих площадей и независимой переменной (приведенной плотности застройки). Учитывая, что введенные корректировки должны были нивелировать влияние на удельные цены, в том числе, факторов масштаба, наличие зависимостей свидетельствовало бы о неточных и (или) неполных корректировках.

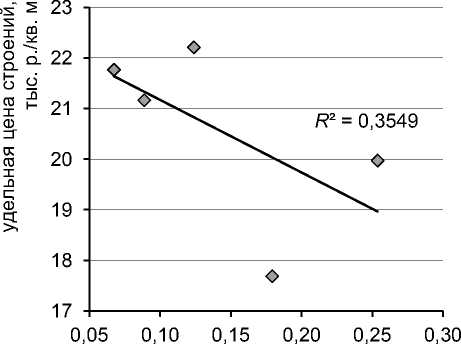
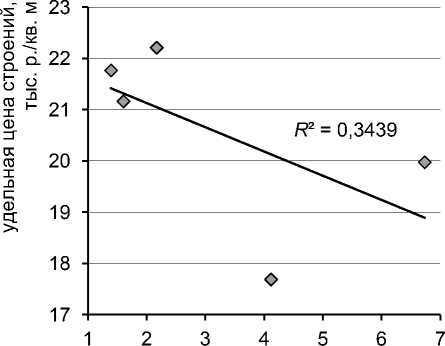
Полагая сначала верной и неизменной для всех аналогов оценку постоянного члена уравнения – удельной стоимости земельных участков a ₀ = 1,1135 тыс. р./кв. м, можно рассчитать по описанному нами алгоритму значения удельных цен улучшений для пяти аналогов застроенных земельных участков и выявить зависимости удельной цены улучшений от приведенной площади строений и скорректированной плотности застройки (рис. 9).

приведенная плотность застройки

приведенная площадь строений, тыс. кв. м

а)                                                   б)

Рис. 9. Зависимость удельной цены строений a ₁ = v_ул : а) от приведенной плотности застройки Q_iB_i / A_iS_i , б) от приведенной площади строений Q_iB_i

Разброс значений коэффициента а _{1 max} / а _{1 min} = 1,26 можно считать умеренным, объяснимым случайной составляющей в рыночных ценах объектов-аналогов.

Однако в обеих зависимостях наблюдается выраженный убывающий тренд, опровергающий допущение о постоянстве коэффициента регрессионного уравнения.

Предположим, что верна (и постоянна) оценка удельной стоимости улучшений a ₁ = 19,798 тыс. р./кв. м, и рассчитаем на ее основе стоимости строений каждого аналога, цены земельного участка как разности цены объекта недвижимости и стоимости строений и, наконец, удельные цены земельных участков. По полученным значениям удельных цен построим зависимости от приведенной плотности застройки и приведенной площади участка (рис. 10).

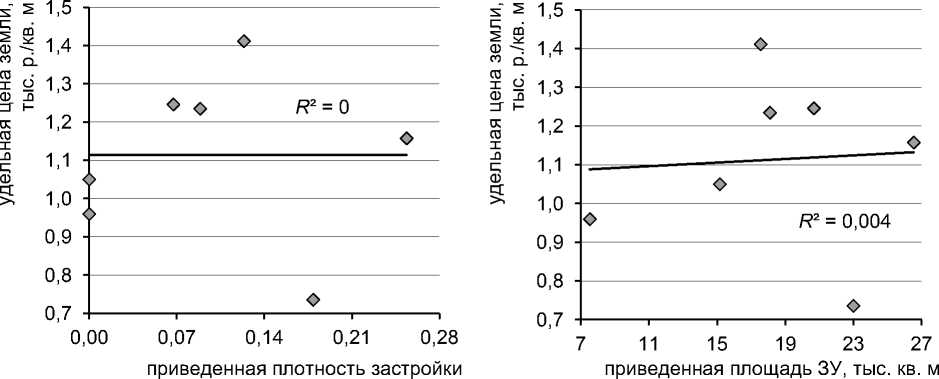
а)

б)

Рис. 10. Зависимость удельной цены земли a ₀ = v_зу : а) от приведенной плотности застройки Q_iB_i / A_iS_i , б) от приведенной площади земельных участков A_iS_i

Какие-либо тренды в полученных зависимостях коэффициента a0 не наблюдаются, что соответствует предположению о его постоянстве, однако разброс его значений недопустимо велик а0 max / а0 min = 1,92. Такой разброс трудно объяснить только наличием случайной составляющей в ценах объектов-аналогов. Об этом могут свидетельствовать и повышенные по сравнению с другими примерами ошибки аппроксимации уравнения ММВ.

Таким образом, полученные зависимости коэффициентов a ₀, a ₁ регрессионного уравнения свидетельствуют о невыполнении предпосылок однофакторной регрессии, в данном случае – о нерешенной до конца задаче введения корректировок.

Это можно показать следующими построениями. При относительно небольших изменениях значений приведенной площади земельных участков и строений (см. табл. 7) зависимости коэффициентов уравнения от приведенной плотности застройки и соответствующих приведенных площадей становятся близкими ожидаемым как по величине разброса, так и по отсутствию выраженных трендов (рис. 11, 12).

Таблица 7

Приведенные площади AiSi и QiBi аналогов при применении ММВ для оценки производственно-складского объекта и их «оптимальные» значения

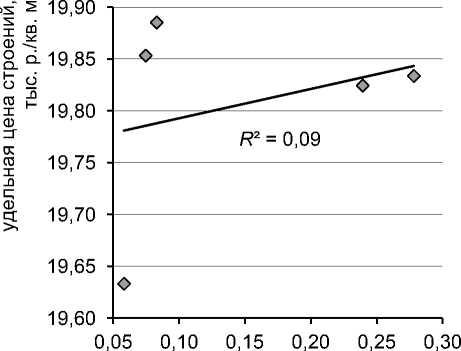
приведенная плотность застройки

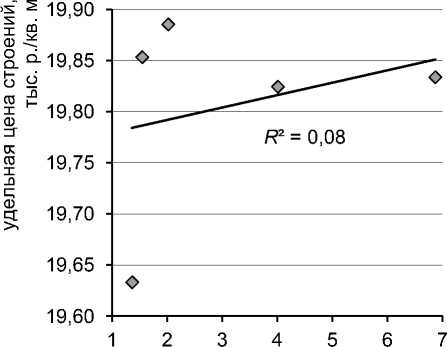
приведенная площадь строений, тыс. кв. м

Аналог	Значения AiSi, кв. м		Изменение величины AiSi, %	Значения QiBi, кв. м		Изменение величины Q i B i , %
	по [9]	«оптимальные»		по [9]	«оптимальные»
1	26 536	24 676	-7	6 864	6 732	-1,9
2	17 550	24 371	39	2 022	2 170	7,3
3	18 094	20 725	15	1 548	1 605	3,7
4	20 680	23 460	13	1 366	1 391	1,8
5	22 990	16 765	-27	4 009	4 116	2,7
6	7 521	6 691	-11	0	0	0
7	15 150	13 428	-11	0	0	0

а)                                                     б)

Рис. 11. Зависимость удельной цены строений a ₁ = v_ул : а) от приведенной плотности застройки Q_iB_i / A_iS_i , б) от приведенной площади строений Q_iB_i

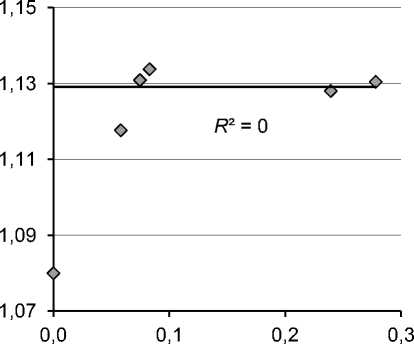
приведенная плотность застройки

приведенная площадь ЗУ, тыс. кв. м

а)                                                    б)

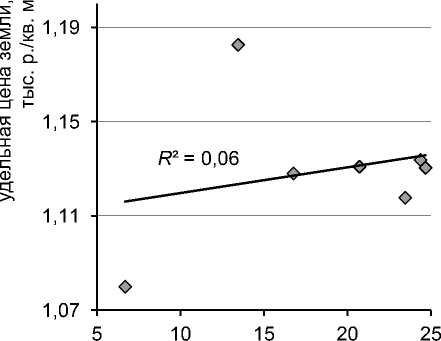
Рис. 12. Зависимость удельной цены земли a ₀ = v_зу : а) от приведенной плотности застройки Q_iB_i / A_iS_i , б) от приведенной площади земельного участка A_iS_i

Как видно, зависимости удельных цен не имеют значимых трендов, а разбросы а _{0 max} / а _{0 min} = 1,1; а _{1 max} / а _{1 min} = 1,01 – минимальны.

«Оптимальные» значения приведенных площадей получены по критерию максимума коэффициента детерминации уравнения ММВ, безотносительно ценообразующих зависимостей. Однако отличия «оптимальных» значений от исходных, рассчитанных введением 10 корректировок, находятся в пределах 7–40 процентов. Изменения в таких пределах вполне возможны из-за ошибок корректировок, точность которых невозможно контролировать.

В связи с этим нельзя считать корректными оценки стоимости земельных участков и строений, полученные в работе [9] с помощью уравнения ММВ.

Отметим в заключение, что рассмотренный в работе [9] пример отличается от других использованием двух групп объектов-аналогов. Наряду с традиционными для ММВ объектами недвижимости (застроенными земельными участками) в выборку включены два незастроенных участка. При оценке земельных участков такое включение резко уменьшает риск существенного смещения оценки стоимости земли в силу построения аппроксимирующей прямой методом наименьших квадратов, «привязывающим» ее к крайним точкам, удаленным от группы других точек.

Но это свойство метода, позволяющее получать оценки стоимости земли, близкие к ценам незастроенных участков, ставит под сомнение саму идею применения ММВ, роль которого сводится к обеспечению статистического оформления такой оценки. Главным условием получения корректных оценок стоимости земли в таких ситуациях является отбор корректных аналогов незастроенных земельных участков, дефицит которых и побуждает к применению ММВ.

Заключение

Внутренним свойством модифицированного метода выделения является использование в качестве коэффициентов регрессионного уравнения удельных цен земельных участков и их капитальных улучшений – экономических величин, подчиняющихся рыночным закономерностям. Следствием этого является высокая чувствительность результатов ММВ к непостоянству удельных цен в используемой выборке аналогов объектов недвижимости, приводящему к смещению оценок стоимости составных частей объекта недвижимости (земельного участка и улучшений).

При этом наблюдается практическая нечувствительность к такому изменению традиционно используемых показателей качества регрессионного уравнения ММВ (коэффициента детерминации, ошибок аппроксимации). При высоких показателях «точности» воспроизведения цен аналогов единых объектов недвижимости оценки составляющих, прежде всего земельных участков, могут быть существенно смещены. А в более общей версии метода (см. [4, 9]) мы не можем быть уверены даже в точном воспроизведении исходных данных, так как уравнение ММВ строится по скорректированным удельным ценам аналогов. Все это требует проведения дополнительных проверок для обеспечения условий получения несмещенных оценок стоимости.

В качестве дополнительный проверки стабильности коэффициентов регрессионного уравнения предлагается алгоритм, который позволяет построить зависимости удельных цен от потенциально влияющих факторов (соответствующих площади и плотности застройки) и оценить условия выполнения допущения о постоянстве коэффициентов.

Шаги алгоритма проверки (начиная с контроля стабильности коэффициента а ₁):

• 1)    значение оценки коэффициента а ₀ (удельной стоимости земли) полученного уравнения принимается как верное и на его основе для каждого аналога рассчитывается оценка стоимости земли: а ₀ → V_зу ;

• 2)    для каждого аналога вычитанием стоимости земельного участка V_зу из цены аналога V_он определяется цена улучшений земельного участка V_ул = V_он – V_зу . Делением полученной цены на площадь улучшений аналога S_ул получаем значение удельной цены улучшений v_ул = V_ул / S_ул (коэффициента а₁ регрессионного уравнения);

• 3)    строятся зависимости коэффициента уравнения от потенциально влияющей площади а ₁ = f( S_ул ) и от коэффициента плотности застройки а ₁ = f( k_пз );

• 4)    процедура повторяется с шага 1 для вычисления и контроля стабильности коэффициента а ₀;

• 5)    по результатам анализа зависимостей по критериям наличия трендов и величине разброса принимается решение о несмещенности оценок и корректности полученной модели ММВ.

Пока не выработаны критерии для величины разброса коэффициентов уравнения и трендов их изменения, обозначающих количественные границы для получения несмещенных оценок стоимости земельных участков (и/или улучшений). Для этого необходимо продолжение исследований чувствительности метода к отклонениям от «идеальных» соотношений. Однако предлагаемая проверка позволяет уже сейчас получать дополнительную информацию для принятия решений на уровне экспертного суждения о допустимости наблюдаемой нестабильности коэффициентов регрессионного уравнения.

Авторы хотели бы отметить еще одну особенность применения ММВ для оценки стоимости земельных участков. Ширина доверительного интервала для среднего значения зависимой переменной (то есть оценки стоимости) минимальна в середине интервала значений влияющего фактора и увеличивается к его краям (см., например, [18]). В ММВ влияющим фактором является коэффициент плотности застройки, принимающий для незастроенного участка нулевое значение. В связи с этим трудно ожидать высокой «точности» (низкой неопределенности) оценок стоимости земли в рамках ММВ с использованием аналогов с относительно высокими значениями плотности застройки.

Учитывая многофакторность рыночного ценообразования, для успешного применения модифицированного метода необходимо предварительно каждый раз решать непростую задачу корректировки цен объектов-аналогов практически по всем факторам за исключе- нием плотности застройки, но включая, как этого требует теория индивидуальной оценки рыночной стоимости, анализ застроенного участка на соответствие его наиболее эффективному использованию.

При этом ошибки корректировок могут свести на нет достоверность результатов предлагаемого регрессионного подхода к оценке земельных участков. Об этом нужно помнить при интерпретации величины среднеквадратической ошибки, полученной после ввода корректировок и не включающей ошибок их определения. Влияние ошибок ввода корректировок на результаты ММВ заслуживает отдельного рассмотрения.

В завершение еще раз напомним, что при реализации ММВ необходимо выполнять все требования к построению корректной регрессионной модели, включая формирование выборки из аналогов, принадлежащих одному сегменту рынка, а также проверку статистической устойчивости модели при подозрении о наличии аналогов-выбросов.

к МЕЖДУНАРОДНАЯ АКАДЕМИЯ ОЦЕНКИ И КОНСТАЛТИНГА

ПРЕДЛАГАЕТ КВАЛИФИЦИРОВАННЫЕ УСЛУГИ ПО ОЦЕНКЕ СЛЕДУЮЩИХ ОБЪЕКТОВ:

• •    предприятий, бизнеса;

• •    пакетов акций, облигаций;

• •    активов предприятий, созданных на основе франчайзинга;

• •    инвестиционных проектов;

• •    дебиторской задолженности;

• •    недвижимого имущества (незавершенных строительных объектов, земельных участков и т.д.);

• •    машин, оборудования и транспортных средств;

• •    интеллектуальной собственности (патентов, товарных знаков и т.д.);

• •    ювелирных изделий и драгоценных камней, антиквариата

Звоните сегодня – +7 (916) 566-32-73; +7 (499) 230-01-09, -02-06

Мы ждем Вас – 115184, г. Москва, переулок Климентовский, дом 1, стр. 1

e-mail наш сайт