Модифицированный метод выделения. Проблемы точности индивидуальной оценки земельных участков

В последнее время отмечается повышение интереса со стороны оценочного сообщества к использованию модифицированного метода выделения (далее – ММВ) (см. [1–5]), который все чаще используется в отчетах об оценке рыночной стоимости земельных участков (далее – также ЗУ) в ситуациях, когда прямых данных о продажах свободных земельных участков недостаточно. Этот интерес объясняется тем, что указанный метод позволяет существенно повысить объем исходной информации за счет привлечения рыночных данных о продажах единых объектов недвижимости, включающих в свой состав земельные участки, сходные с оцениваемым. В соответствии с логикой статистического оценивания увеличение объема исходных данных должно привести к повышению точности оценки. Однако расчеты стандартной ошибки для оценки земельного участка, основанные на традиционных формулах линейной регрессии, реализованных в среде Excel, не подтвердили ожидания. Даже при маленьком разбросе цен относительно регрессионной прямой (коэффициент детерминации больше 0,95) стандартная ошибка оценки удельной стоимости земельного участка, определяемая в процентах от оцененной стоимости, достаточно большая. Это снижает эффективность метода и ограничивает его применение. На это обратил внимание С.В. Грибовский, который представил соответствующие расчеты, показывающие на примере, взятом из работы Л.А. Лейфе-ра и Т.В. Крайниковой [5], что относительная величина стандартной ошибки оценки земельного участка приближается к 15 процентам.

В настоящей статье проводится анализ причин низкой точности, приводится их объяснение, а также предлагаются направления дальнейшего развития метода, обеспечивающие его эффективное применение.

Краткая историческая справка

Исследуемый в статье модифицированный метод выделения был предложен в работе [1]. Метод предназначен для того, чтобы проводить одновременную оценку земельного участка (далее также – ЗУ) и объекта капитального строительства (далее также – ОКС), используя в качестве исходных данных цены предложений (сделок) единых объектов недвижимости, содержащих в своем составе сходные земельные участки и ОКС. Суть метода состояла в ре- шении регрессионной задачи, в которой связывается удельная стоимость единого объекта недвижимости и плотность застройки. В.Г. Мисовец в работе [6] обратил внимание на возможности широкого применения этого метода и привел примеры использования метода для различных сегментов недвижимости. Это дало толчок к применению метода практикующими оценщиками.

В первоначальной версии область применения ММВ была ограничена однородными объектами, а прямое его использование для неоднородных исходных данных приводило к большим ошибкам. Дальнейшее развитие метод получил в 2015 году в работах [3, 4], в которых было предложено расширить модель модифицированного метода выделения на случай, когда ОКС и земельные участки, входящие в состав объектов-аналогов, отличаются от объекта оценки, содержащего сходные составляющие, отдельными характеристиками. С этой целью в модель были добавлены корректирующие коэффициенты, относящиеся к ОКС и земельным участкам. В результате такой процедуры была создана усовершенствованная версия базового метода, которая объединила идеи, реализованные в двух методах сравнительного подхода: методе, основанном на регрессионном анализе, и методе корректировок. При этом усовершенствованная версия сохранила достоинства и недостатки указанных методов. От метода корректировок она заимствовала процедуру приведения сходных объектов (объектов-аналогов) к объекту оценки, если сходные объекты близки по ценовым параметрам и характеру ценообразования. Сохранились и проблемы, обусловленные неопределенностью корректирующих коэффициентов.

Усовершенствованная версия ММВ применительно к задаче оценки стоимости земельного участка имеет ряд преимуществ по сравнению с традиционным методом сравнения продаж. Метод позволяет, оставаясь в рамках сравнительного подхода, наряду с ценами продаж сходных земельных участков (прямых объектов-аналогов) использовать для оценки ЗУ рыночные данные о единых объектах недвижимости (далее также – ЕОН), содержащих сходные участки. Таким образом, использование регрессионного анализа позволило дополнить исходную выборку данными о продаже единых объектов, включающих ЗУ, сходные с объектом оценки. Во многих случаях это позволяет увеличить объем используемой информации, поскольку таких данных, как правило, значительно больше. Как известно, точность статистической оценки при использовании эффективных процедур обработки данных взрастает с увеличением количества информации, содержащейся в выборке (см., например, неравенство Рао-Крамера 1). В связи с этим следует ожидать, что использование дополнительных данных о единых объектах недвижимости должно повысить точность оценки по сравнению с оценкой, использующей только данные о продажах земельных участков.

В предложенном виде ММВ нашел применение в практике оценки земельных участков и объектов капитального строительства. Результат проведенного нами опроса оценщиков показал, что отчеты с использованием модифицированного метода выделения выполнялись для различных целей и задач заказчика. Он применялся оценщиками в различных городах и для различных сегментов недвижимости (производственно-складская, офисно-торговая, жилые дома с надворными постройками и так далее). Особо следует отметить, что модифицированный метод выделения включен в состав ряда методических разработок (см., например, [7]).

Регрессионная модель, лежащая в основе метода

Основу метода составляет соотношение скорректированной удельной стоимо- сти единого объекта и скорректированной плотности застройки сходных объектов недвижимости:

где У , =

V i

A i x S i

– цена объекта-аналога,

V i

A i x S i

= p +

B , x Q.

—----'- x c ,

A i x S i

где ρ – оценка удельной рыночной стоимости земельного участка объекта оценки;

с – оценка удельной рыночной стоимости ОКС объекта оценки;

S_i – площадь земельного участка ЗУ объекта-аналога (в составе ЕОН или свободного);

Q_i – площадь ОКС объекта-аналога (в составе ЕОН);

V_i – цена единого объекта недвижимости объекта-аналога;

n – количество объектов, используемое в качестве аналогов;

A_i – коэффициент, равный произведению корректировок удельной цены по различным параметрам сравнения, по которым оцениваемый земельный участок отличается от соответствующего объекта-аналога (с индексом i );

B_i – коэффициент, равный произведению корректировок удельной цены по различным параметрам сравнения, по которым оцениваемый объект капитального строительства отличается от соответствующего объекта-аналога (с индексом i ).

Цены и площади, относящиеся к объектам-аналогам, обозначаются индексом i , причем i = 1, …, n .

отнесенная к площади земельного участка (с учетом корректировок);

B, x Q,

X: = —---- - плотность застройки объек- i Aix Si та-аналога (с учетом корректировок),

ɛ_i – случайная составляющая цены (в регрессионном анализе ее называют случайной ошибкой), связанная со случайными, неконтролируемыми параметрами ценообразования. Как и во всех моделях такого типа предполагается, что математическое ожидание случайной величины равно нулю.

Следует отметить, что характер случайной ошибки и ее связь со значением регрессора являются важнейшими факторами, определяющими точность оценки. Обычно оценщики не придают этому значение и по умолчанию используют модель регрессии с постоянной дисперсией случайной составляющей D ( ɛ_i ) = σ ².

В эконометрике показано, что в этом случае стандартная ошибка оценки удельной стоимости земельного участка в классическом варианте метода наименьших квадратов (далее также – МНК) определяется следующим образом:

m p

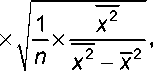
Если рассматривать значение скоррек-

B , x Q, тированной плотности застройки ⁱⁱ как

A i x S i независимую переменную (факторный при-

где чертой над х ² обозначается операция усреднения, а σ – стандартное отклонение, которое обычно неизвестно априори, но может быть оценено на основе статистических данных по формуле:

знак или предиктор), а скорректированную

удельную стоимость

V i

A i x S i

как зависимую

_a = I E ( У , - Y ) 2

N n - 2

переменную, то мы приходим к уравнению

регрессии, которое можно записать в традиционной форме:

где Y_i – прогнозное значение удельной стоимости ЕОН объекта-аналога.

y_i = p + cx_i + ɛ_i ,

Еще раз напоминаем, что формулы (3) и (4) получены в предположении, что дис-

персия ошибки постоянна (не зависит от x и от y ).

Численный пример задачи оценки рыночной стоимости земельного участка с помощью модифицированного метода выделения

Приведенный далее пример позволяет увидеть проблемы, связанные с использованием формул (3) и (4). В качестве исходных воспользуемся данными из нашей публикации [5], на основе которых проводил расчет погрешности оценки земельного участка С.В. Грибовский. В таблице 1 приведены исходные данные: скорректированные цены двух незастроенных участков, скорректированные цены единых объектов недвижимости и соответствующие им скорректированные плотности застройки, расчетная величина прогнозного значения ( Y_i ), а также остатки, возведенные в квадрат ( Y i – y i )².

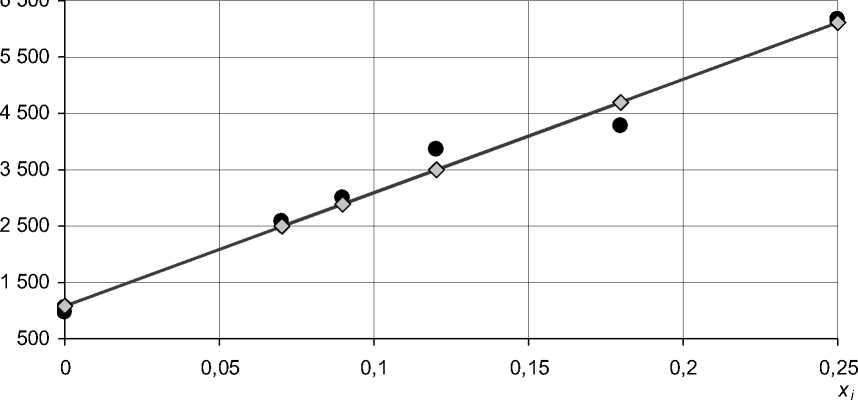
Как видно из таблицы 1 и графика, приведенного на рисунке 1, пересечение регрессионной прямой с осью ординат, соответствующее значению удельной стоимости оцениваемого земельного участка, равно 1 097 р.

При этом стандартная ошибка, которая вычисляется по формулам (3) и (4), равна 156 рублям, или 14,3 процента (156 / 1097), тогда доверительный интервал с вероятностью 95 процентов составит [1 497, 697] р./кв. м. Такой же результат показывает и расчет в среде MS Excel, поскольку в ней также реализуется упрощенная модель регрессии. Здесь следует отметить, что рассчитанные по формулам (4) и (5) значения стандартной ошибки параметра и стандартного отклонения являются несмещенными оценками соответствующих характеристик, а не их точными значениями. Тем не менее такой результат, как справедливо отметил С.В. Грибовский, при таких исходных данных нельзя признать удовлетворительным. К этому следует добавить, что полученная стандартная ошибка (выраженная в процентах) в два раза превышает ошибку аппроксимации, что само по себе представляется странным.

Разберемся в приводящих к этому причинах.

О нарушении допущений, лежащих в основе регрессионной модели

Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие (в смыс-

Таблица 1

Исходные данные [5]

№ объекта-аналога	Зависимая переменная yi, р. / кв. м	Независимая переменная xi, относительные единицы	Прогнозное значение Yi, р./кв. м	Квадраты остатков ( Y i – y i )2 , ( р. / кв. м )2
1	6 180	0,250	6 104,0	5 820,22
2	3 859	0,120	3 500,2	129 004,02
3	2 991	0,090	2 899,3	8 403,24
4	2 577	0,070	2 498,8	6 180,76
5	4 280	0,180	4 701,9	177 927,50
6	959	0,00	1 096,7	18 834,01
7	1 050	0,00	1 096,7	2 180,62
Среднее значение	3 128	0,101	–	–

• исходные данные

О регрессионная прямая у = 1 097 + 20 029 x

Рис. 1. График регрессионной прямой по классическому методу наименьших квадратов и исходные данные

ле минимума дисперсии) оценки в классе линейных оценок, случайная ошибка ɛ_i должна удовлетворять определенным условиям, известным как условия Гаусса-Маркова.

Первое условие – математическое ожидание ( μ ) случайной ошибки ɛ_i при любом значении регрессора должно быть равно нулю:

μ(ɛi) = 0, где i = 1, ..., n.

Это означает, что иногда случайная ошибка будет положительной, иногда отрицательной. Другими словами, в значениях цен предложений, так же как и цен сделок, всегда присутствуют неконтролируемые параметры, которые могут увеличивать или уменьшать цены аналогов. При этом они не должны иметь систематического смещения. Наличие такого смещения может исказить результат оценки. Это важно понимать при интерпретации результата. Однако если уравнение регрессии включает свободный член, то это смещение войдет в качестве слагаемого в свободный член, поэтому первое условие можно считать всегда выполненным.

Второе условие – это условие некоррелированности ошибок состоит в том, что предполагается отсутствие систематической связи между значениями случайной составляющей в любых двух наблюдениях, то есть ковариация величин ɛ_i и ɛ_j равна нулю:

сov( ɛ_i , ɛ_j ) = 0.

Случайные факторы, влияющие на цену, должны быть независимы друг от друга, то есть ковариация между ними должна быть равна нулю. В данном случае можно признать, что это условия выполняется.

Третье условие (Гаусса-Маркова) – дисперсия ( D ) случайной составляющей не зависит от значения независимой переменной и постоянна для всех наблюдений:

D(ɛi) = σ2 = const, где i = 1, ..., n.

Это условие называется гомоскедастич-ностью (homoscedasticity).

Если условие гомоскедастичности нарушается, то оценки коэффициентов регрессии не будут наилучшими, оставаясь при этом несмещенными. На анализ этого условия очень редко обращают внимание практикующие оценщики, несмотря на его важность для корректного применения регрессионных моделей. Нарушение гомоске-дастичности приводит, с одной стороны, к тому, что расчет стандартных ошибок по формулам (3) и (4) не отражает реального состояния дел, с другой – к тому, что метод наименьших квадратов при нарушении условия гомоскедастичности не обеспечивает получение оценок с наименьшей дисперсией.

Здесь это нарушение имеет место. Природа ценообразования на рынке такова, что разброс значений цен относительно их среднего значения обычно растет с увеличением среднего значения. Действительно, здравый смысл подсказывает, что объекты, имеющие более высокую рыночную стоимость, имеют и больший разброс цен (в абсолютном выражении), чем объекты с низкой стоимостью. При этом в процентном выражении разброс цен обычно не зависит от величины стоимости и сохраняется примерно постоянным во всем сегменте. Имеются и статистические подтверждения этого факта. Из этого следует, что при прочих равных условиях рыночные цены ЕОН, в которых стоимостная доля ОКС более высокая, чаще всего будут иметь большее грессионной модели это означает и возрастание дисперсии цен объектов-аналогов, отнесенных к значениям площади земельного участка (с учетом корректировок) yi при увеличении значений плотности застройки.

К этому следует добавить, что указанное нарушение гомоскедастичности обычно проявляется и при анализе остатков, и приведенный пример не является исключением.

Рассмотрим, как ведут себя остатки в нашем примере. Используя данные таблицы 1, построим поле корреляции (см. рис. 2), на котором в качестве независимой переменой используются значения скорректированной плотности застройки, а в качестве зависимой переменной представлены значения остатков, возведенные в квадрат ( Y i – y i )².

Как видно из графика (см. рис. 2), значения остатков в среднем увеличиваются при увеличении прогнозного значения. В области небольших значений скорректированной плотности х расчетные остатки в среднем значительно меньше. Грубая прикидка показывает, что стандартное отклонение, характеризующее разброс значений остатков, для малых значений плотности застройки не превышает 8,5 процента, а при

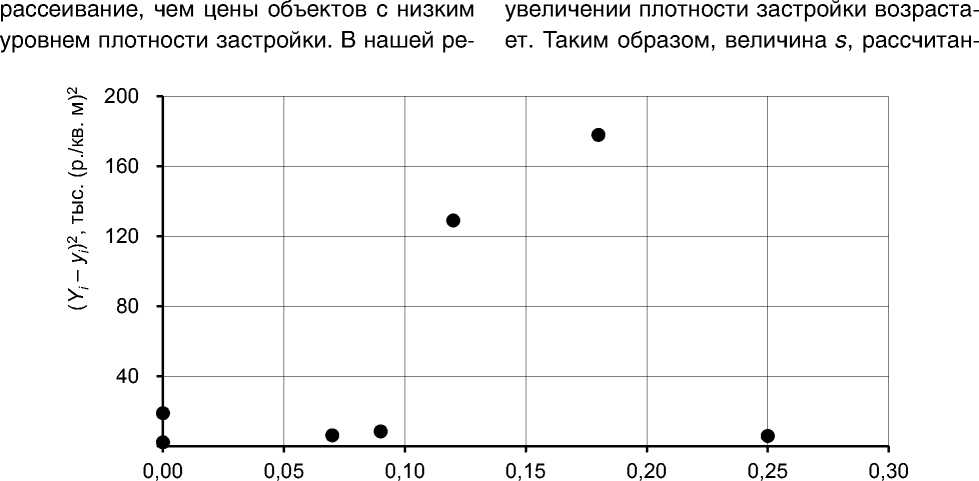
x i

Рис. 2. Зависимость квадрата остатков от величины x

ная по формуле (4) посредством усреднения по всем значениям остатков, не может рассматриваться в качестве стандартной ошибки, относящейся к оценке при х = 0. Исходя из изложенного такой результат не является неожиданным: объекты, характеризующиеся более высокой плотностью застройки и поэтому имеющие более высокую стоимость, имеют и больший разброс цен (в абсолютном выражении), чем объекты, имеющие меньшую стоимостью.

Нарушение гомоскедастичности в задачах, связанных с оценкой недвижимости, и необходимость это учитывать отмечал в своих работах Н.П. Баринов (см. [8]). К сожалению, этот факт зачастую игнорируется оценщиками, использующими упрощенные модели регрессии, «зашитые» в MS Excel, вследствие чего стандартная ошибка рассчитывается некорректно.

Таким образом, в приведенном примере наблюдается существенное нарушение условия гомоскедастичности. Формулы (3) и (4), по которым рассчитывается стандартная ошибка, приводят к значительному завышению погрешности оценки свободного члена, который интерпретируется как удельная стоимость земельного участка.

Однако нарушение условия гомоскеда-стичности не означает, что модифицированный метод выделения, основанный на регрессионной модели, не может быть реализован. Эти трудности можно преодолеть, если использовать взвешенный метод наименьших квадратов.

ММВ на основе взвешенного метода наименьших квадратов

Вопросам проведения регрессионного анализа в условиях гетерокседатичности посвящено много публикаций (см., например, [9]). При нарушении гомоскедастич-ности рекомендуется традиционный метод наименьших квадратов заменять взвешенным методом (далее – ВНМК). Этот метод применяется к определенным образом преобразованным данным. Он лишен уже указанного недостатка и позволяет получать оценки, характеризующиеся минимальной дисперсией в классе линейных несмещенных оценок. Для начала рассмотрим случай, когда дисперсии σi2 случайной составляющей ɛi, различающиеся для разных значений факторного признака xi, известны. Можно устранить гетероскеда-стичность, разделив каждое наблюдение на соответствующее ему значение σi2. Тогда дисперсия случайной величины ɛi / σi2 будет представляться в виде:

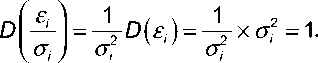
Для уменьшения неоднородности дисперсии разделим все переменные на σ_i и получим регрессионное уравнение:

y_i / σ_i = ρ / σ_i + c ( x_i / σ_i ) + ɛ_i / σ_i . (5)

Как мы уже показали, дисперсия случайной ошибки ɛ_i / σ_i для этого уравнения будет постоянной и может быть оценена стандартными формулами (3) и (4).

Однако на практике в задачах оценки недвижимости дисперсия случайной составляющей σi2 обычно неизвестна. Это делает невозможным прямое использование предложенного подхода. Преодолеть эти трудности можно, если сделать определенные допущения относительно дисперсии случайной составляющей. Как уже отмечалось, рассеивание цен, выраженное как стандартное отклонение, обычно растет пропорционально значению цены объекта недвижимости. При этом стандартное отклонение в процентном выражении может оставаться постоянным. Проведенные нами исследования подтверждают это предположение. Такое же предположение можно сделать о разбросе цен ЕОН, отнесенных к площади земельного участка. В этом случае для получения наилучшей линейной оценки параметров регрессии можно воспользоваться взвешенным методом наименьших квадратов, который в данном случае может быть легко реализован.

В соответствии с принятым допущением запишем:

уравнения, получим следующие формулы для параметров ρ и c :

ρ = y _w - c x _w ;

^ = K ^x Y ,                            (6)

где K – коэффициент пропорциональности;

Y – прогнозное значение, полученное с помощью регрессионной модели, лежащей в основе метода, то есть с помощью классического метода наименьших квадратов.

c =

xy w - x w y w

Тогда дисперсия o f вычисляется по формуле:

0 = K ² x У, ² ,                           (7)

где o f - дисперсия ошибки при конкретном -м значении фактора.

Отметим, что эти формулы по структуре такие же, как при традиционном методе наименьших квадратов с той лишь разницей, что средние значения заменены на средневзвешенные.

В результате значение искомого параметра ρ составит 1 018 р./кв. м. Получившаяся регрессионная прямая представлена на рисунке 3 вместе со значениями исходных данных.

Стандартные ошибки коэффициентов рассчитываются по формулам, также схожим по структуре с классическим методом наименьших квадратов:

С учетом (6) регрессионное уравнение (5) принимает вид:

m ρ

1 = K

∑ ^w

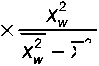
; x_w

y / Y = ρ / Y + c ( x / Y ) + e / Y .         (8)

Уравнение (8) с преобразованными переменами отвечает условию гомоскедастич-ности и для нахождения коэффициентов регрессии можно воспользоваться тради-

m c

×

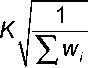
—2 x w ^- x w

ционным методом наименьших квадратов. Для компактного представления оценок

параметров регрессионного уравнения вве-

дем следующие обозначения:

весовой коэффициент w_i =

Y ■

• cредневзвешенные значения величин:

∑ ^wi^xi      ∑ w i y i

• x w _∑ w_i ; y w _∑ w_i ;

• -т _Е wixi.— _£ w ху x_w =         ; xy_w =

∑ w    ^w  ∑ w

Используя традиционную процедуру определени я параметров регрессионного

Проблема вычисления стандартных ошибок заключается в том, что значение K нам неизвестно. Этот коэффициент можно определить с помощью регрессии, используя в качестве независимой переменой квадрат остатков ( Y – y )², а в качестве регрессора – Y . После извлечения из него корня, мы получим К = 0,052 (см. рис. 4).

Для нашего примера стандартная ошибка коэффициента ρ (удельной цены земельного участка) m_ρ будет равняться 39,4 р./кв. м, или 3,9 процента, что существенно ниже, чем аналогичная ошибка, рассчитанная традиционным МНК.

Отметим также, что переменная дисперсия для расчета ВМНК может быть задана другим способом, например как функция x .

* н ижний индекс w в этой формуле и в формуле (6) означает, что операция усреднения осуществляется с весовыми коэффициентами.

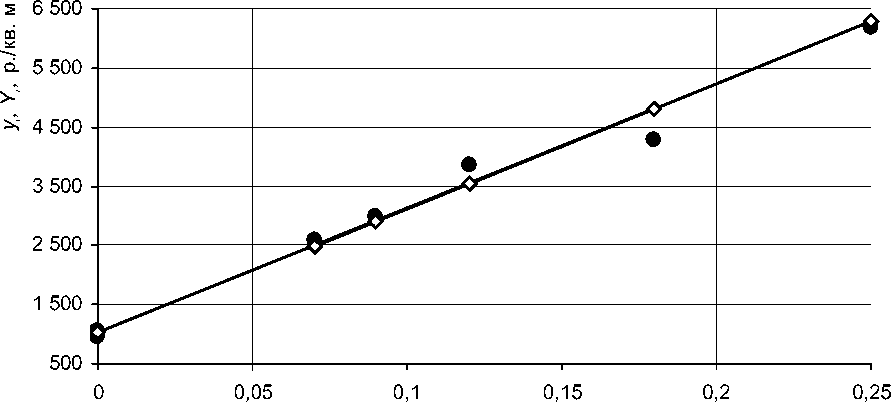
• исходные данные —о—регрессионная прямая у = 1 018 + 21 035 x

Рис. 3. График регрессионной прямой по взвешенному методу наименьших квадратов и исходные данные

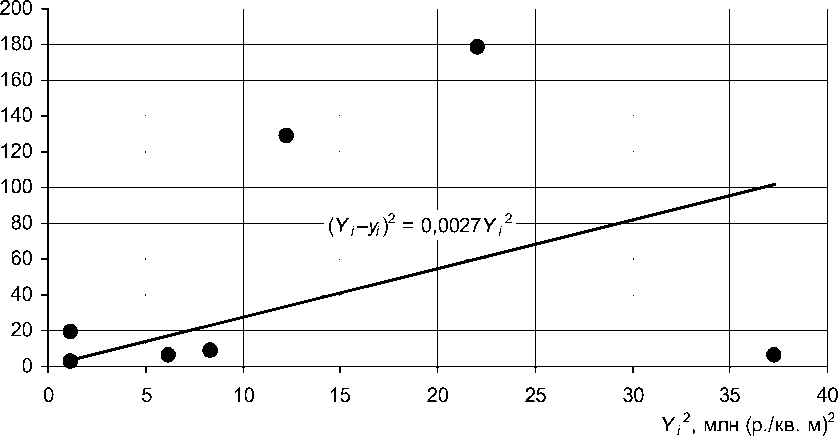
Рис. 4. Зависимость квадрата остатков от Y _i ²

ММВ на основе минимизации средней ошибки аппроксимации

Другой распространенной характеристикой точности модифицированного метода выделения является средняя ошибка аппроксимации, равная среднему значению относительных отклонений расчетных значений от статистических.

Расчет средней ошибки аппроксимации на основании данных традиционного МНК из примера [5] дает среднее значение 6,47 процента (см. табл. 2).

Такая характеристика в наибольшей степени отражает точность метода, если стандартное отклонение случайной составляющей пропорционально прогнозному значению целевой функции у в регрессионном уравнении, поэтому для повышения точности оценки по этому критерию следует найти такие параметры модели, которые минимизируют среднюю ошибку аппроксимации Q :

1 Q = _n ¹ ∑

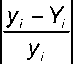
→ min .

Таблица 2

Пример расчета ошибки аппроксимации и остатков [5]

№ объекта-аналога	Зависимая переменная yi, р. / кв. м	Независимая переменная xi , относительные единицы	Прогнозное значение Yi , р. / кв. м	Остатки Y i – y i , р. / кв. м	Ошибка аппроксимации ( Yi – yi ) / yi , %
1	6 180	0,250	6 104,0	-76,29	1,2
2	3 859	0,120	3 500,2	-359,17	9,3
3	2 991	0,090	2 899,3	-91,67	3,1
4	2 577	0,070	2 498,8	-78,62	3,1
5	4 280	0,180	4 701,9	421,81	9,9
6	959	0,00	1 096,7	137,24	14,3
7	1 050	0,00	1 096,7	46,70	4,4
Среднее значение	3 128	0,101	–	–	6,47
Дисперсия остатков				58 058,39

Таким образом, задача оценки удельной стоимости земельного участка и оценки удельной стоимости ОКС в рамках ММВ сводится к минимизации суммы модулей относительных отклонений:

∑

y_i - ρ + cx

yi

→ min .

Решение этой задачи можно реализовывать при помощи надстройки MS Excel «Поиск решения», где в качестве целевой функции будем задавать среднюю ошибку аппроксимации.

Для выполнения надстройки «Поиск решения» на изменяемые значения накладываются ограничения, вводимые специалистом-оценщиком. Для того чтобы их определить, нужно рассмотреть значения c , получившиеся с использованием традиционного метода наименьших квадратов, и подобрать не противоречащие им ограничения.

В MC Ecxel встроены три метода расчета оптимального значения:

• •    нелинейный метод обобщенного понижающего градиента (ОПГ);

• •    симплекс-метод;

• •    эволюционный метод.

Выбор того или иного метода определяется конкретными характеристиками данных и наличием априорной информации, которой располагает оценщик.

В нашем примере был использован эволюционный метод.

Минимизация ошибки аппроксимации в надстройке «Поиск решения» дала результаты, представленные в таблице 3.

В результате значение искомого параметра ρ составит 1 050 р./кв. м (см. рис. 5).

Таким образом, применение этого метода позволило оценить регрессионное уравнение с точностью, измеряемой средней ошибкой аппроксимации, равной 5 процентам. С учетом принятого допущения о том, что стандартное отклонение случайной ошибки пропорционально значению регрессии при каждом значении скорректированной плотности, полученным значением средней ошибки аппроксимации можно характеризовать точность оценки удельной стоимости земельного участка.

Заключение

В статье предложено дальнейшее совершенствование модифицированного метода выделения. Усовершенствованный метод

Таблица 3

Результаты метода «Минимальная ошибка аппроксимации» на данных [5]

№ объекта-аналога	Зависимая переменная yi, р. / кв. м	Независимая переменная xi, относительные единицы	Прогнозное значение Yi , р. / кв. м	Остатки Y i – y i , р. / кв. м	Ошибка аппроксимации ( Yi – yi ) / yi, %
1	6 180	0,250	6 441	67 809	0,04
2	3 859	0,120	3 638	49 218	0,06
3	2991	0,090	2 991	0	0,00
4	2 577	0,070	2 559	323	0,01
5	4 280	0,180	4 931	424 000	0,15
6	959	0,00	1 050	8 194	0,09
7	1 050	0,00	1 050	0	0,00
Среднее значение	3 128	0,101	–	78 506	0,05
y - ρ + cx Целевая функция ∑ i      → min y					0,35

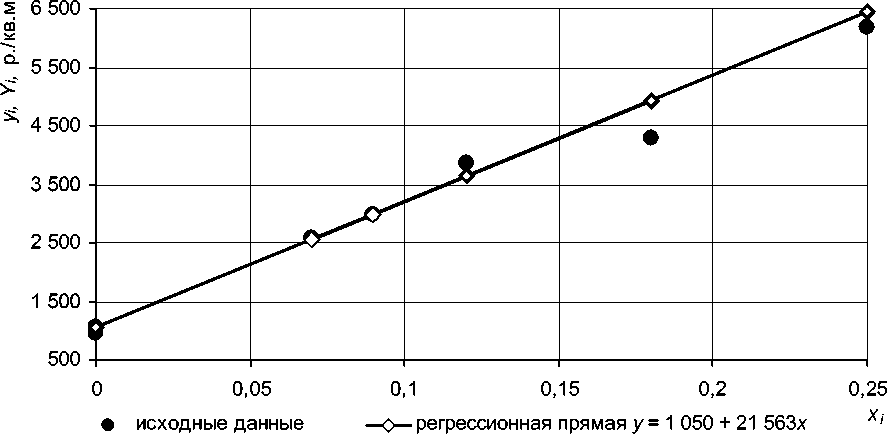
Рис. 5. График регрессионной прямой по методу минимальной ошибки аппроксимации и исходные данные

позволяет обеспечить оценку земельных участков в условиях гетероскедастичности остатков. Представлены две версии ММВ, одна из которых основывается на взвешенном (обобщенном) методе наименьших квадратов, другая на минимизации среднего значения модуля относительной ошибки. На конкретном примере приведены расчеты точности по обеим версиям. Оба изложенных альтернативных метода расчета стандартной ошибки оценки земельного участка подтверждают эффективность модифицированного метода выделения при оценке земельных участков, также как ОКС. Следует отметить, что один или даже несколько примеров не являются доказательством эффективности методов. Их следует рассматривать только как иллюстрацию методов и способов их применения. Приведенные методы основываются на классических методах математической статистики и, в частности, ее разделов, относящихся к методологии регрессионного анализа. Строгое обоснование корректности изложенных методов приведено в соответствующей литературе.

Следует отметить, что точность оценки стандартной ошибки при увеличении количества исходных данных быстро повышается. В связи с этим метод может быть рекомендован при массовой оценке, в частности, для определения кадастровой стоимости.

Авторы выражают глубокую признательность доктору технических наук, профессору С.В. Грибовскому, чьи критические замечания помогли исправить отдельные положения статьи. Особенно полезными для авторов были дискуссии, касающиеся области применения взвешенного (обобщенного) метода наименьших квадратов в задачах оценки недвижимости, за что мы выражаем отдельную благодарность.