Модификация итерационной факторизации для численного решения двух эллиптических уравнений второго порядка в прямоугольной области

Рассматривается два эллиптических дифференциальных уравнения второго порядка в прямоугольной области со сторонами параллельными осям координат. При этом на правой и верхней сторонах прямоугольной области задано главное краевое условие, а на остальной части границы задано естественное краевое условие. При достаточно гладких данных и, как следствие, гладких решениях эти уравнения сводятся к уравнению Пуассона, экранированному уравнению Пуассона. Для разностных аналогов этих уравнений в виде систем линейных алгебраических уравнений приводится факторизующийся переобуславливатель попеременно треугольного вида при модификации [1]. Эта методика аналогична модификации метода фиктивных компонент, предложенной и изучаемой в [2]. Дискретные задачи такого вида могут быть также получены в методе типа фиктивных компонент при решении более сложных задач в [2, 3]. Решаемые в работе разностные уравнения получаются и при численном решении эллиптического дифференциального уравнения уже четвертого порядка в [4].

Первая и вторая непрерывные задачи

Рассматриваются две задачи ua е W: А„(ua,v) = la(v) Vve W, la e W‘, a = 1,2,                      (1)

где соболевское пространство функций

W = W(Q) = {v e W2(Q): vr = 0} на прямоугольной области

Q = (0; b 1 ) x (0; b 2 ), с Г_{1 =}{ b } x [0; b 2 ]U[0; b j x { b ₂ } , билинейные формы

^A a ^{( u} , ^v ) = J ^{( u} x ^v x ^{+ u} y ^v y ^{+ ( a -} 1) ^cuv ) d ^Q

Q и заданы константы b1, b2 > 0, c > 0.

Заметим, основываясь на [5-7], что решение каждой задачи из (1) существует и единственно. Если la(v) = JfavdQ,r = dQ, Г2 =r\Г1, Q где fa - заданные действительные достаточно гладкие функции, то задачи из (1) представляются в следующем виде

-A U a + ( a - 1) cu a = f a , U a I г = 0, ^ u ^ lr₂ = 0, a = 1,2.                   (2)

¹          d n ²

Ушаков А.П.

Модификация итерационной факторизации для численного решения двух эллиптических уравнений второго порядка в прямоугольной области

Можно отметить, что в (2) уравнения с точностью до знака совпадают с уравнением Пуассона, когда a = 1, с экранированным уравнением Пуассона, когда a = 2.

Первая и вторая дискретные задачи

Рассматриваются системы линейных алгебраических уравнений, получающиеся при дискретизации (1), (2) на основе метода сумматорных тождеств u е RN: Au = f , f е RN, a = 1,2,                        (3)

a          a a J a a где векторы va е RN : va = (va 1,..., vaN)‘, N = m • n, m , n е N, при этом считается, что va,m(j—1)+i va,i,j , i 1,..., m , j 1,..., n , а va i j - являются значениями функции дискретного аргумента, соответствующего узлам сетки (x, yj) = ((i — 0,5)h1, (j — 0,5)h2), i, j е X, шаги сетки h1 = b /(m + 0,5), h2 = b2/(n + 0,5), состоящей из указанных выше узлов, а матрицы Aa размерности N х N определяются следующим образом:

^{+ (} u a , i , j + 1 ^— u a , i , j ^{)( v} a i , j + 1 ^— v a , i , j ) ^h 2 2 ^{+ ( a —} 1) ^cu a , i , j ^v a ,i , j ) ^h 1 ^h 2 , u a , i,n + 1 = v a , i,n + 1 = ⁰, i = ¹,"-, ^m , u a , m + 1, j = v a , m + 1, j = ⁰, ^j = ¹,"-, n ^.

Здесь ^.,.) - скалярное произведение векторов следующего вида

N

\u _a , v _a / = £ u a , k ^v a ,k ^h 1 ^h 2 ^V u _a , v _a ^{е R} N .

k = 1

Если функции fa непрерывны на области Q, то возможно положить fa,i,j = f(xi,yj), i = 1,...,m, j = 1,...,n.

Решение каждой задачи из (3) существует и единственно, т.к. A _a >  0, a = 1, 2.

Фиктивные продолжения дискретных задач и их решений

Выбираются фиктивные продолжения для (3)

u е R^{2 N} : Du = f , f е R^{2 N} , f ₍ - i = 0, a = 1,2,                      (4)

где векторы v е R2N : v = (v ', v ')‘, j , 2      , блочная, верхнетреугольная матрица D размерности 2N х 2N такова, что Dn = A = А1, D12 = О, D21 = 0, D22 =A = A2, матрицы

6> = v'V -V'V A = V 'V +V'V x y y x , x ' x ^{1 v} y ¹ y , а матрицы V _x , V _y размерности N х N определяются следующим образом

(Vxua,va) = ]££(—(uai +1,j — ua,i,j)hf1 va,i,j)h1 h2, ua,m+1,j = va,m+1,j = 0, j = 1,-,n, i=1 j=1

(^V y u _a , v _a } = 2 m £ ^{( — (} u a i , j + 1 ^{— u} a i , j ) ^h 2^{1 v} a , i , j ) ^h 1 h 2 , u a , i , n + 1 = ^v a , i , n + 1 = ⁰, i = ¹,-, m .

i = 1 j = 1

Введём подпространства векторов в пространстве R^{2 N} :

Математика

V 1 = { v = ( v /, v₂'):v ₂ = 0 } , V 2 = { v = ( v /, v^S : Av ₁ - 9 v ₂ = 0 ] .

Утверждение 1. Решение каждой задачи из (4) u е V _a , a = 1, 2, существует и единственно.

Итерационная факторизация на фиктивных продолжениях

Определим блочную матрицу С размерности 2 N х 2 N такую, что

С 11 = с 22 = A , С 12 =-9 , С 21 = 9 .

Для решения задач из (4) предлагаются итерационные процессы:

u^k е Ж^{2 N} : С ( u^k - u^{k - 1}) = - T _k ( Du^{k - 1} - f ), k е N, T _k >  0 V u ⁰ е V _a , a = 1,2.         (

Заметим, что в итерационных процессах из (5) возникают задачи с факторизуещимся оператором и следующего вида

U е C N : LL*U = F , F е C N , при этом возможно расщепление на более простые задачи

Wе CN : LW = F, Fе CN, U е CN: L*U = W, W е CN , где матрицы

‘

L = ^y - i^ v , L = L = ^y + i^ v , x y      xy

LL = (^y - i^v )(^y + i^v) = A + i9, xyxy тогда

(A + i9)( u1 + zu2) = f1 + if,, что равносильно:

Au - 9u = f, u + iu = U,

1           2 ^J ’      1          2           ,

,9u ₁ + Au 2 = f , , f + if , = F

• и, действительно, на каждом шаге итерационных процессов из (5) возникают задачи типа cu = f , u = ( u 1 , u _;y, f = ( f 1; f /у.

Утверждение 2. Если в итерационных процессах из (5) u k ^{- 1} = u , то u k = u V k е N .

Пусть u^k = u +V k V k е NU{0}.

Утверждение 3. В итерационных процессах из (5)

AVk - 9v2 = (1 - Tk) (AVk-1 - 6Vk2-1), если a = 1, t1 = 1, то Vk е V2 Vk е N, если a = 2, то Vk е V2 Vk е N U {0}.

Введём нормы

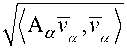
, a = 1, 2.

Замечание 1. Имеют место неравенства

Э5е [1; +^): A < А < 5 A,

. 2

п где 5 = 1 + сХ , Х = 2,25(b 2 + b22) = Х11(1,1)<Х11(m,n)< lim Х11(m,n) =   Х, а собственные

^{,            ,}             m , n ^~ ^,             9

числа матрицы A из [1]:

^Х , j ⁽ m , n ) =

2 m + 1 ] ^b 1 J

■ 2I (2 i - 1) П sin ----—

2(2 m + 1)

2n)

I b2 )

■ 2 [ (2 j - 1) п sin ———

( 2(2 n + 1)

.

Утверждение 4. Имеет место равенство

CС^,^ = (А^2,^2>-{AW^ VVе V2

Доказательство. Учитывая, что

AV1 - 9у2 = 0, 9 = -9, получается

Ушаков А.Л.               Модификация итерационной факторизации для численного решения двух эллиптических уравнений второго порядка в прямоугольной области { СУ, у) = (^^1, ^2 ) + ( АУ2 ’ У2 ) = ^У2 ) + ( A^2^2 ) =

= ( A ^ 2 ^ 2 ) ^- № У 1) = ( A ^ 2 ^ 2 ) ^- ( ^А У 1 У 1) .

Предположение 1. (О фиктивном продолжении) Имеет место неравенство

3« 1 e (0;1): ( Av ), v )} <  « 1 ^A v ₂ , v ₂) V v e V₂.

Можно отметить ( у = (1 - a , ) ¹ или « 1 = 1 - у ^{- 1}), что

Э Ye (1; +^ ): ( Av ₂ , v ₂) <  /( Cv , v ) = / (( Av 2 , v ₂) -( Av ), v ) }) V v e V ₂ , т.к. матрица A >  0, а из [8] и матрица С >  0 . А именно в нашем случае выводится, что

(Cv,V ) = (Vxv! - Vyv2 )2 + (Vy v1 + Vxv2)2 > 0 VV ф 0 , последнее, т.к. (Vx + iVy)(v1 + iv2) Ф 0 Vv Ф 0 . Также отметим, что

Э Л ¹ е (0; +^ ): 0 < ( Av ), v j = ( ^ v ₂ , v )) = ^ A '^ v ₂ , ^ v ₂^ <  Л ¹ ( ^ v ₂ , ^ v ₂) ^ 0, при h 1 , h ₂ ^ 0, где опять Л = Л i (1,1) = 2,25( b 1 ^{- 2} + b ₂ ²), т.е.

(Av 1 , v ^ ^ 0 , v 1 ^ 0 , т.к. ^ v ₂ = ( v _x 'V y - V y 'V _x ) v ₂ ^ 0, при h 1 , h ₂ ^ 0 V v e V₂ .

Утверждение 5. Имеют место неравенства

1 - a

----¹ ( ^А У 1 ’ У 1) <  ^{(1 -} « 1)( A V 2 ^ 2^ < ( ^СУ ’ У ) ^V V ^e V 2 .

« 1

Доказательство. Используя, что

(АуУ < «1 Wi^ Vye V2

получаем

1 - « 1 « 1

(А У 1 , У 1) <  (1 - « 1 )( A ^ 2 , ^ 2> = ( A ^ 2 , ^ 2> - « 1 (A ^ 2 , ^ 2> <

<( A ^ 2 , ^ 2> -( А У 1 , У 1) = ( C y , y V y e V 2 .

Утверждение 6. Если в итерационном процессе из (5) a = 1, k = 1, Т1 = 1, то имеют место оценки

СС^,^^ < -«1-(a^10,^10) = (Y-1)(Су0^0V l^1 < -«1-k0|| = (Y-1)1 k .

' ^Z 1 - « 1                                          A 1 - « 1      A              A

Доказательство. Из итерационного процесса имеем

С (Vх-у0) = - Dy °, (с (у1 -у 0\у1^ = (су1,^1) = -( Dy 0^Y = -( AVi^Y < HI Al У1! А ’ тогда

¹ (У1\< ^{A y} 1 ^{, У 1} /л^⁰         « 1                « 1 /с^⁰

\ ^{С у , У} / < /     1 1 \ \ ^{A y} 1 ^{, у} 1 / <  ч \ ^{A y} 1 ^{, у} 1 / = ч \^{С у , У}

'        ' Ссух,Уу ' 1 -«1х ' 1 -«1'

учитывая, что

(А у \ , У 1¹) <  « 1 ( с у 2 , У 2), ( с у ¹, У ¹) = ( A y 2 , У 2) -( А У 1 ¹, У 1¹) ^ (1 - « 1)( A y 2 , У 2 Из утверждения 5.

^{1 -} « 1                           « 1

----¹ ( А у_ьУ 1 )<( С у , у ) = —( С у 1 , У 1 ),

« 1^{х               х} '   ^{1 -} « 1 ^х '

следовательно, выполняется вторая оценка.

Утверждение 7. Имеют место неравенства

С Су,У < 

Доказательство. Заметим,

1 -«         1 -«

—yDD^y,y)< -^^(АУ2,У2>< (1 -«1)(Ау2,у!)< (Су,у = = ( Ау2,у2)-(АУ1,У1) <(Лу2,У2) = (Dy,y,

Математика

что и требовалось доказать.

Утверждение 8. Если в итерационных процессах из (5) а Ф 1 или к Ф1, 22 δ-1 +α γδ-1 0 <τ_k=τ=    <  , q =¹=<1,

1 +γδ γδ    δ+1-α1 γδ+1

то

C Cy^k ,^) < q 2 (c^k^-1,^^к-1), к е N.

Доказательство. Из итерационных процессов получается, что

C(ψk-ψk-1)=-τDψk-1, ψk=Tψk-1, T=E-τC-1D, T =T′>0, тогда

/С^^к,^^к\ = СсТу^к 1,Ty^k1\< sup ^^CT^,T^ ^C^k 1^^k1\ = ψ∈V₂Cψ,ψ

=sup ψ∈V₂

=sup ψ∈V₂

' (CTy,^ V _vCCy,^ ,

Cψ^k-1,ψ^k-1=sup

ψ∈V₂

f ((C - TDT >v^ f

I   (C^.^ J

Cψk-1,ψk-1 ₌

f1 - TD^ T ( (C^.^ J

Cψ^k-1,ψ^k-1=max{1-τ²1-τγδ²}Cψ^k-1,ψ^k-1=q²Cψ^k-1,ψ^k-1.

Теорема 1. В итерационных процессах из (5)

u_α^k -u_αΑα≤ε_αu_α⁰-u_αΑα,

при получается, что

Т1 = (2 - а) + (а - 1)т, тк = т, к е N \ {1},

ε_α ≤ ((2-α)(γ-1) +(α-1) γδq)q^k-1 .

Доказательство. Если а = 1, то из утверждения 5 имеем

1 - α₁ α₁

(АуъУ1^ < (С^) V^e V2,

а из утверждения 6 следует Cψ¹,ψ¹≤

α¹   Aψ₁⁰,ψ₁⁰=(γ-1)Aψ₁⁰,ψ₁⁰.

Если α= 2, то из утверждения 7 получается 1-α

¹Αψ₂,ψ₂≤ Cψ,ψ, Cψ,ψ≤Αψ₂,ψ₂∀ψ∈V₂. δ

Вывод. Учитывая вид матриц L, L*, можно отметить, что для решения задач из (3) с N неизвестными, на основании приведенной теоремы 1, предложенными итерационными процессами из (5) с относительными погрешностями ε_α, требуется не более чем O(Nlnε_α^-1)арифметических операций.