Модификация кватернионного метода описания поворотов с помощью ортогональных проекций

Кватернионы являются сравнительно новым, но уже зарекомендовавшим себя математическим инструментом современной физики. С помощью кватернионов удалось достигнуть прогресса в описании такого понятия квантовой механики, как спинор [1-3]. Понятие кватернионных пространств оказывается плодотворным в применении к описанию целого ряда физических объектов -от систем отсчета до полей и собственно пространств [4]. Одним из простейших, но весьма иллюстративных примеров применения кватернионов является описание ньютоновской механики в системе отсчёта наблюдателя, представленной кватернионным репером. В частности, для произвольно вращающейся системы отсчета, неинерциальное движение которой складывается из ускоренных трансляций тела отсчёта и любых вращений координатных осей, удобным оказывается рассмотрение кватернионных базисов (Q-триад) направляющих оси координат, и их поворотов. Более глубокий кватернионный анализ позволяет описывать и ситуацию с ускоренным движением тела отсчёта наблюдателя [4]. Именно на языке кватернионов Дж. Максвелл впервые записал свои уравнения электродинамики, и оказалось, что записанные в кватернионной форме вакуумные уравнения Максвелла являются аналогом условий Коши-Римана, то есть записав уравнение типа Коши-Римана, обобщающее условия аналитичности функции комплексного переменного на функцию гиперкомплексного переменного, можно получить в точности систему уравнений электродинамики Максвелла [4]. В работе [5] показано, что преобразование Хопфа можно удобно представить в терминологии кватернионов. Очень удобным оказывается описание понятий дифференциальной геометрии в физике с применением кватернионов, таких как кручение [4] и сравнительно простого вывода соотношений сферической геометрии [4,6].

Широкое распространение получили кватернионы при описании поворотов в решении физических задач (кинематических задач ориентации твердого тела [6]. Квантово-механические результаты, основанные на теории кватернионов нашли и практическое применение в астрономии [7].

Решение задачи описания поворотов вектора вокруг оси в пространстве аналитическими методами весьма сложна. Одним из возможных подходов к решению таких задач является операторный метод [8] (когда вектор умножается на матрицу некоторого унитарного оператора, но для нахождения матрицы оператора необходимо найти результаты поворота трех базисных векторов, что тоже требует немалых усилий). И.Л. Кантором, А.С. Солодовниковым [9] был предложен метод описания поворотов при помощи кватернионов.

В этой работе показано, что если р — это некоторый нормированный вектор (т.е. вектор, длина которого равна 1), а 。一 это произвольный вектор, который перпендикулярен вектору р, то умножением 。 слева на кватернион q = cos g + р sin g осуществляется поворот вектора 。 вокруг оси р на угол g.

Действительно, если q = q + bi + cj + dk - это произвольный кватернион, модуль которого равен 1, то q ² + b² + c² + d² = 1.

Запишем, что q = q + q‘, г де q‘ — это вектор bi + cj + dk. Из то го, что |q| ² + |q‘|² = 1 следует существование такого угла g, что q = cos g, |q‘| = sin g.

Очевидно, что q‘ = |q‘|p, где р есть вектор длины 1. Значит, q = cosg + рsing.

Теперь умножим кватернион q на некоторый векторный кватернион ^, причём рассмотрим тот случай, когда вектор 。 перпендикулярен вектору р. Получаем:

q 。 = (cos g + р sin g) 。 = 。 cos g + р 。 sin g.

Так как р перпендикулярен 。， то произведение р 。 имеет действительную часть, равную нулю, а векторная часть равна вектору длины |р|| 。 ] sin ^ = | 。 |, который перпеидикуляреи р и 。 и ориентирован относительно ри 。 тем же образом, что ориентирован и вектор k относительно i и j. Обозначим этот вектор через и. Можно сказать, что вектор u получается из 。 поворотом вокруг вектора рн а 2. Таким обра’зт ， получаем следутотттее равенство ： q 。 = 。 cos g+u sin g. Договоримся.

что поворот вокруг р — это поворот в том направлении, в котором осуществляется кратчайший поворот от г к j (вокруг к) — это правило обычно известно как «правило правой руки».

Таким образом, приходим к выводу, что вектор qv получается поворотом вектора 。 на угол g вокруг оси вектора р. Однако, такое правило работает не для произвольного вектора, а лишь для вектора v. который перпендикулярен р.

Для того, чтобы представить в кватернионной форме поворот вокруг оси р вообще любого вектора v. необходимо усложнить действия над вектором v. Нужно ^заменить обычное умііожеіше на q слева более сложным выражением qvq-1. где q-1 является кватернионом. обратным q. то есть таким, что qq-1 = 1.

q ^-1 = cos 夕 一 р sin / так как

(cos / + р sin g)(cos / - р sin /) = cos² / - р² sin² / = cos² / + sin² / = 1.

qvq^-1 = qv cos / + qu sin /.

Правая часть равенства — это вектор, который получен из qv поворотом на угол / вокруг оси р. А так как вектор qv получается из v тем 本 е поворотом, что ii qvq ^-1 из вектора qv. то вектор qvq^-1 получается из v повороте)м на угол 2/ вокруг оси р.

Итак, произвольный вектор v при повороте на угол 2/ вокруг оси р переходит в вектор qvq^-1, где q = cosg+рsing [9]. При этом необходимо не ： забыть поделить реальный угол поворота на 2. что достаточно часто существенно усложняет вычисления (например, вместо поворота на табличный угол 45 ° приходится выполнять вычисления с углом 22, 5 ° ii т.п.).

Но этот способ является весьма громоздким. В ходе решения задачи этим методом приходится осуществлять сложные вычисления, в результате которых можно допустить много арифметических ошибок.

• 1.    Результаты и обсуждение

В настоящей работе мы предлагаем другой, более рациональный с нашей точки зрения, способ решения задач данного типа. Идея метода состоит в нахождении проекции вращаемого вектора на ось вращения и разложении его на сумму ортогональной проекции и ортогональной составляющей. В силу линейности операции вращения [10] можно осуществить поворот каждого слагаемого отдельно. Но очевидно, что результатом вращения ортогональной проекции (как вектора лежащего на оси вращения) будет сам этот вектор. Поэтому проекция при повороте не изменится. Ортогональная же составляющая как раз будет являться вектором, ортогональным к оси вращения, поэтому для описания поворота ортогональной составляющей достаточно будет применить умно жение на кватернион слева, как это описано выше. Нахождение ортогональной проекции и ортогональной составляющей осуществляется при помощи алгоритма, описанного в работах Проскурякова И.В. [11], Шевцова Г.С. [12]. Сравним оба способа решения на примере нахождения результата поворота вектора т(1, 3, 5) вокруг вектора д(—1,0,1) на у гол ^.

Задача. Дан вектор т(1 , 3 , 5). Найти коордипаты вектора 立 который получится при повороте вектора т на угол 2 вокруг вектора д(—1,0,1).

Предварительно проверим, не являются ли векторы т и g ортогональными. Очевидно, что их скалярное произведение (вычисленное стандартным образом: (т, g) = 1 ・(一 1)+3 ・ 0+5Т = — 1+5 = 4 не равно 0. следовательно, векторы не ортогональны.

Далее нужно нормировать вектор g(—1,0,1). Для этого разделим его на его норму, которая равна У (—1)2 + 02 + 12 = ут = 通

• ^g = / 2 ( ?| ^і + 击 ^j + 击幻

  Примем за ось вращения вектор q = ? 2 * + ? 2 J

  
  

+ ♦-

Так как векторы т и у не ортогональны, искомый вектор t = qxq^-1. Здесь q-1 — кватернион, обратный q.

q

cos g + p sin g

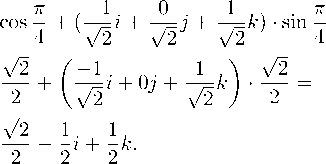
q^-1 = cos g — p sin g

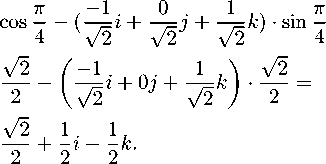
Далее воспользуемся правилом умножения кватернионов и таблицей умножения мнимых единиц и получим следующее:

qvq-1

√ ₂ ²

- 2ⁱ+2 "•^{( i}+3^j+5^k )•首 +2ⁱ - 2^k

)

+

+

+

( (

(

-----i

1 і 2 +1 .І+3^2 L 3 І, + 3 封+憂左 22  2  22  2

=i + 二 + 二+ j - 3 k - 2   22   2   2

3 І + 5^2 左 + 5, 222

- 5 泌 + 5 餡］ /С + 1 i - 1 力

2  2   222

- 5 ) • ( 5+1 і - 1"=

- 2+

- 2+

2 - 3   3 2+6

i+—^j+

5^√2 - 3      ^√2

丁 “三+

2i - 2 "

2 - 3 2   6+6 2    10 - 3 2

i+--j+

2 - 3 ^k-i+^^

i2 +34+6 ji +

旦 2- 上近+厶一s泳一冬2泳- 5^ 餡= 4   44   4

2 - 3 ^√ 2   6+6 ^√ 2    10 - 3 ^√ 2       ^√ 2 - 3

■ ¹               ■ j +--:....... k - i--:.....

- 2+

分 +

3 2+6

—^k+

5 2 - 3           2 - 3

^j+^k+^^^j -

- 4^√2 - ^√2+3+5^√2 - 3

3 2+6   5 2 - 3

-i+

+

2 - 3 2 - 4 - 3 2 -

⁶ І+

6+6 2+5 2 - 3+ 2 - 3

j +

10 - 3 2 - 3 2 - 6+4

..................:.................k

- 8 - 6 2    12 2    8 - 6 2

-₄—ⁱ + ； ^j +

k = ⁽-” - 2 ) і + 3 凡 + (-” + 2 ) k.

Значит, вектор t имеет координаты (— 322 — 2, 3V2, — 322 + 2).

Второй способ: Разложим наш вектор т на два слагаемых: т = w + г, где вектор w коллинеарен оси вращения g(w = су), а г — ортогонален ей (вектор г — ортогональная составляющая, а вектор w — ортогональная проекция).

т = су + г

Подставим полученные выражения в формулу нахождения скалярного произведения двух векторов и преобразуем:

( Т, у) = (су + Z, у) = с®, у) + (z, у).

Так как z и у - ортогональны, поеледиее слагаемое равно 0. Следовательно, (т, у) = с(у,у).

Т.к. скалярное произведение (т, у) = 4, а (у, у) = 2, получим 4 = 2с. Значит, с = 2.

Тогда w = 2( - 1,0,1) = ( - 2, 0, 2), z = т - ^ = (1,3, 5) - ( - 2, 0, 2) = (3, 3, 3).

При вращении суммы векторов слагаемое z поворачивается вокруг оси q = 击 (- ， + 0/ + к) на угол равный 2, а елагаемое w не изменяется (как лежащее на оси вращения).

В таком случае результат поворота можно найти как qz + w = —(-г + к)(3, + 3/ + 3к) + (-2, + 2к)=

= 二( 一 3,² - 3,/ - 3 注 + 3кг + 3к/ + 3к² ) + ( - 2, + 2к)=

= 二( 3 - 3к + 3/ + 3/ - 3, - 3) + ( - 2, + 2к)=

3 .      6 .       3 ,

--, +--/--к — 2, + 2к х/2   N 陋

- 3 - 2х/2 .   6 .    - 3 + 2 通，

......7=...., +..ž= / +--7=....k

4/2

(- 呼- 2 ) , + 3 通/ +

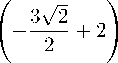
к

Значит, искомый вектор 力 имеет координаты (-322 — 2 , 3 V2 , — 322 + 2).

Очевидно, что второй способ требует существенно меньше вычислений. Однако, нельзя исключать и первый способ, например, для автоматических систем. Если умножение на кватернион осуществлять при помощи матриц на ЭВМ (матричный метод умножения можно найти в работе Мальцева [8, С. 93]), то алгоритмическая реализация первого способа может оказаться более простой, чем у второго. Так ли это на самом деле, является вопросом для дальнейшего исследования.

Заключение

Кватернионы являются полезным и эффективным инструментом для математического описания пространственных поворотов, что необходимо для решения ряда физических задач. Каждому повороту можно сопоставить кватернион единичной длины в своего рода п тригонометрической форме" — аргументом служит угол поворота, а в качестве пмнимой единицып выступает единичный вектор, лежащий на оси вращения. В таком случае, результат поворота удобно вычисляется путем разложения вращаемого вектора на ортогональную проекцию на ось вращения (которая при вращении остается неизменной) и ортогональную составляющую (результат поворота которой можно вычислить, умножив ее на соответствующий повороту кватернион).