Модификация математического аппарата почти периодического анализа для обработки пространственно-временных данных с упорядоченным аргументом

В настоящее время в области прикладной математики исследуется применение почти периодических функций для обработки данных, которые представляются в виде дискретной функции с упорядоченным аргументом, в качестве которого может выступать, например, время или пространственная характеристика. Проведены исследования теоретических свойств почти периодических функций. В работах рассматривались вопросы, связанные с изучением почти периодических функций в различных метрических пространствах, а также исследована сходимость рядов Фурье почти периодических функций [1–4].

В работах [5–7] показаны возможности почти периодических функций для обработки результатов измерений в областях химии, физики и биологии. Общая концепция обработки эмпирических результатов измерений с упорядоченным аргументом представлена в работах [8, 9]. Однако в представленных исследованиях анализировались одномерные ряды с упорядоченным аргументом, где динамика процесса протекала только вдоль, например, временной оси.

Для изучения возможностей обработки и анализа пространственно-временных данных представлен обзор имеющихся моделей и методов, позволяющих работать с представленным форматом данных. По результатам исследований автор приходит к выводу о необходимости создания и применения новых моделей и методов для поиска взаимосвязей между многопараметрическими характеристиками, изменяющимися во времени и в пространстве [10].

В качестве данных с пространственно-временными характеристиками рассмотрены фото- и видеоряды динамики тропических циклонов, применение к которым почти периодического анализа дало качественные результаты задачи мониторинга и прогнозирования чрезвычайных ситуаций в области техносферной безопасности [11-13].

В исследовании приведены особенности математического аппарата почти периодического анализа для обработки и анализа динамики тропических циклонов по спутниковым изображениям.

Основная часть

В данной работе рассматривается математический аппарат почти периодического анализа для обработки и анализа изображений динамики тропических циклонов.

Обрабатываемые изображения представляют собой матрицу пикселей, которые принимают значения от 0 до 255. Размер исходного изображения составляет 500 х 500 пикселей. Особенности применения почти периодического анализа к центрическим структурам на изображениях подробно описаны в работе [13].

Особенностью применения почти периодического анализа к таким данным является предобработка исходных данных путём преобразования изображения из декартовой системы координат в полярную систему координат согласно выражениям р (x, у ) = ^(xc - x)2 +(yc - y )2 , Ө (x, y) = arctan yc—y ,

где x c , y c - декартовы координаты центра преобразования; x, у - преобразуемые декартовы координаты пикселя; р , Ө - длина радиус-вектора и угла в полярных координатах.

Для применения такого численного преобразования стоит учесть ряд особенностей, связанных со структурой представления изображения. В качестве исходных данных имеем сетку узлов значений функции яркости, которые представляются пикселями изображения. Для перехода в полярные координаты возможно выбрать произвольную точку вне узлов и построить радиус-вектор к любой точке, что позволит определить и длину, и угол этого радиус-вектора. Но при наложении сети полярных координат на сетку функции яркости в узлах изображения получается неравномерная картинка - многие узлы прямоугольной сетки не попадут в узлы равномерных полярных координат (рис. 1).

Тогда для перехода в полярные координаты сначала необходимо создать сетку полярных координат, то есть определить радиус и количество угловой насечки, затем рассчитать значения функции яркости в новой позиции, для этого необходимо сделать несколько шагов.

Шаг 1. Определяются 4 узла прямоугольной сетки, которые «обрамляют» узел полярной сетки, иногда это может быть 2 узла, если радиус-вектор лёг ровно по горизонтали или вертикали, а иногда и 1 узел - когда идёт «чистое» совпадение. Пример возможного расположения узлов прямоугольной сетки относительно узла сетки полярных координат представлен на рис. 2.

Шаг 2. Проводится процесс интерполирования полученных значений. Значение яркости функции в каждом узле будем соотносить с буквой узла (см. рис. 2) - то есть яркость в пикселе А равна f k . Координаты красной точки назовём x k , y k . Спроецируем положение красного узла на отрезки АВ и CD (рис. 3).

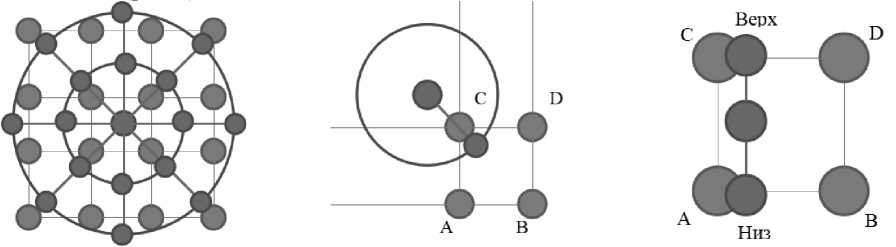
Рис. 1. Наложение сетки значений функции яркости в узлах изображения и сетки полярных координат

Рис. 2. Пример возможного расположения узлов прямоугольной сетки относительно узла сетки полярных координат

Рис. 3. Проекция положения узла полярных координат на декартовы

Проводим интерполяцию внутри каждого отрезка и определяем значение в верхнем и нижнем красных узлах:

Математика

f^ =f c + ( f D - f c ) 'A x, Лиз =f A + ( / в - f A У*Х ■                (2)

Стоит отметить, что Ax = xk - xC = xk - xA, поскольку координаты точек А и С совпадают. Проводя интерполяцию между двумя этими значениями (2) уже по оси у, получаем выражение fk = f +(fex — Лиз )-ЛУ.                           (3)

На основе описанных преобразований становится возможным перевести изображение из декартовых координат в полярные для дальнейшего применения к полученным данным почти пе- риодического анализа.

После предобработки данные изображения анализируются по срезам вдоль полярных углов, такой вектор содержит значения пикселей по радиус-векторам при фиксированном угле. Каждый такой вектор поочерёдно обрабатывается обобщённой сдвиговой функцией, которая лежит в ос- нове почти периодического анализа.

Особенности выявления почти периодов из дискретных данных на основе сдвиговых функций описаны в работах [8-9].

Сдвиговая функция, применяемая для обработки дискретного ряда данных, описывается вы- ражением следующего вида:

!   N-т a (т ) = ^~^\f ( t + Т)-f ( t )| ’                             (4)

N ^{- Т} t =1

где N - общее число отсчётов функции f(t t ); t - упорядоченный аргумент дискретной функции f(t t );

т - проверяемые значения почти периодов.

Для выявления почти периодов необходимо учитывать форму анализируемых колебаний, для этого вводится понятие обобщённой сдвиговой функции. Пример обобщённой сдвиговой функции с учётом геометрического способа исключения тренда представлен формулой а (т, At) =

N - т - 2 A t

N-т -2A t

Z t=1

ln

Л yt-At+т yt+At+т

k

У 2+?

У

-

ln

Л yt-At yt+At

k     У 2     У

,

где т - значения почти периодов; A t - значения сдвига по аргументу; N - количество отсчётов функции.

При обработке временных рядов небольших размерностей было достаточно использования численного итерационного алгоритма вычисления обобщённой сдвиговой функции, где каждое значение массива a ( т , A t ) рассчитывалось в ходе отдельной итерации циклов. В контексте обработки больших данных, а также медиаданных встала необходимость усовершенствования алгоритмов по вычислению обобщённой сдвиговой функции.

Первой предложенной модификацией стал алгоритм исключения тренда из данных. Проведение операции по исключению тренда можно проводить, вычисляя сразу целый вектор колебаний для фиксированного значения сдвига A t :

P a t

= ln

^yt -A t ' ^yt +A t

y_t ²

где P - вектор значений колебаний, полученный по результатам исключения тренда на основе теории пропорций, размерностью N-2At; yt - вектор значений yt; yt-At - вектор значений yt-at; yt+at - вектор значений yt+At.

Тогда расчёт сдвиговой функции (4) для фиксированного значения Δt также можно представить в векторном виде:

a ^(т ) A t = N - т - 2 A t ^{P a} t ^{+ т -} P ^A t                             ⁽⁷⁾

где а ( т )_д? - вектор сдвиговой функции для вектора колебаний со сдвигом по аргументу A t ; P _{A t+T} - вектор исключенного тренда при значении A t , смещённый на т ; P _{A t} - вектор исключенного тренда при значении A t .

В (7) операция модуля является перегруженной, то есть результат модуля разности векторов P _{A t+T} и P _{A t} представляет собой вектор абсолютных величин.

В результате таких преобразований, получаем, что набор векторов вычисленных сдвиговых функций a ( т )_Л( есть результат обобщённой сдвиговой функции (5).

Заключение

Таким образом, проведенные математические преобразования с алгоритмами анализа пространственно-временных характеристик тропических циклонов позволили модифицировать вычисления, осуществляемые почти периодическим анализом данных с упорядоченным аргументом на основе сдвиговых функций, что позволило на качественном уровне и с приемлемой скоростью обработки данных получать результаты анализа центрических структур, присущих опасным природным явлениям, по спутниковым изображениям.