Модификация TVD схемы для отрицательной скорости движения одномерной ударной волны

Актуальной проблемой при численном моделировании сверхзвуковых течений газа является корректное воспроизведение движения ударных волн. В настоящее время для расчета таких течений широко используются методы, построенные на так называемых TVD схемах [1, 2] решения уравнений Эйлера для сжимаемого невязкого газа. Одним из недостатков данных методов является наличие численной вязкости, приводящей к размазыванию фронтов ударных волн. В работах [1, 2] предлагаются схемы TVD второго порядка точности, имеющие существенно меньшую численную вязкость по сравнению со схемами первого порядка точности. Однако предложенные схемы не сохраняют точность при смене направления движения ударной волны. В данной работе рассматривается модификация TVD схемы, предложенной в работе [2], как имеющей немного меньшую численную вязкость на ударной волне, хотя с помощью данного подхода можно модифицировать и схему из работы [1].

1. ЧИСЛЕННАЯ СХЕМА МЕТОДА

Здесь

w _

p                 о m f (w) _ uw + p

V E )

,

V pu;

,

где u - скорость, p - плотность, m _ p u - импульс, E – полная удельная энергия, p – давление, x – координата, t – время.

Система уравнений (1) замыкается с помо-

щью уравнения состояния для идеального газа p _ (к-1)p(E--2 pu2) ,          (3)

где к - показатель адиабаты, для воздуха к _ 1.4 . Собственные значения матрицы Якобиана

5 f(w)

A(w) _                   (4)

dw

определяются, как

X 1 _ u - c X 2 _ u X ₃ _ u + c ,

где c – скорость звука:

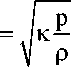
Запишем уравнения Эйлера движения сжимаемого вязкого газа в потоковой форме [1]

Соответствующие правые собственные торы находятся следующим образом

Г i )            ( I )

век-

d w + d f(w) _ о S t      d x

R i^{(w) _}

u - c

H - uc

, R 2^{(w) _}

u

¹ u ²

,

Никонов Валерий Владимирович, кандидат технических наук, старший преподаватель кафедры конструкции и проектирования летательных аппаратов.

R 3^{(w) _}

u + c

V H + uc ,

,

где H – полная энтальпия:

H = (E + р)/ р = с ² / ( к- 1) + |u ² .

Введем следующие обозначения для конечных разностей

^[b] = b j + i ^- b j •                 (8)

и средних величин

(b) = !(b j + b j + 1 ) .              (9)

Тогда мы можем записать левые собственные векторы-строки Li , умноженные на вектор столбец конечных разностей переменных (2), в следующем виде a1 , = L1 w. , = i(C -C ), j+ 2 Д J+ 2     2 v 12

a 2|+1 = L2a w|+1 = [р] — C,(10)

J +2

a3 , = L3.w. , = KC + C2), j+1        Д J+ 2     2 v 12

где

C 1 = ( к- 1) ( [E] + У*2 [ р ] - u * [m] ) /с *²

C2 =([m] - u*[p])/с*.(11)

Здесь используется осреднение по Roe [1, 3]:

u*+1 =(Vpu)/( W) ,(12)

H*+1 ^VpH)^ W) ,(13)

c*+1 = V(к- 1)(H*+1- iuVi).

TVD схема согласно [2] описывается следующими формулами:

wn+1 = wn-f1 (^ -fl-1) •<

J J 2дx x j+2

fj+2 = i(f(wj) + f(wJ+1)-dj+2) •(16)

d ,= 2AxVpkRk ,(17)

j+2        t 2—1 ' и 2 j+2 •

P^ 1 = Q(v^ +Y k 1 ) « k - (g k + g k + 1 ) • (18)

⁺ 2              ^{J +} 2        ^{J +} 2 ^{J +} 2

vk+1 = yt- MwJ+D •

J+2 2 д x с ограничителем значения функции:

gk — sk 1 max[0,min( ak 1 , aVjj/S • (20) J         J+ 2                           \ J+ 2 J 2 J+ 2 / где sk+1 — sign(ak+1),(21)

vk ''2 -gk)/ak+ 2, ak+1 * 0

^{J + 1} I 0, a k + ₂ — 0

Q(z) — z2 + 4(23)

Модификация схемы заключается в зеркаль- ном отражении относительно узла j данных *

w , передаваемых в подпрограмму для вычис- ления членов d , выражения (17), и кусственной вязКОСти, если m < 0 :

d 1 ис- j₂

P * ^— P j m * — - m_j ^E* — ^Ej *

,

*

^р j - 1 ^{— р} j + 1

^m* - 1 ^{— - m}j + 1

*

^ej - 1 ^{— e}j + 1

Р * - 1 ^— P j + 1  >

,

*

^р j + 1 ^{— р} j - 1

*

m j + 1 ^{— - m}j - 1

( ^pJ + 1 ^{— p}J - 1 J

^P j - 2     ^p j + 2

m j - 2 ^— - m j + 2

E *

E j - 2    E j + 2

*

I P j - 2 ^— P j + 2 J

*

^P j + 2     ^P j - 2

m * + 2 ^— - m j - 2

E *

E j + 2    E j - 2

*

I P j + 2 ^— P j - 2 J

для об-

После вычисления членов d d j+2 • J-ращенной задачи необходимо поменять знаки у тех из них, которые отвечают за изменение количества движения в уравнении (16), так как знак у скорости ранее был изменен на обратный.

• 2.    НЕКОТОРЫЕ ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Модифицированная TVD схема тестировалась на широко известной задаче [1, 3] со следующими начальными условиями (НУ).

p 0 — 1 u 0 — 0 p 0 — 1 • если X j <  0

p 0 — 0.1 u 0 — 0 p 0 — 0.125 , если x_j >  0 . (26) ,                      ,

Область моделирования принималась равной x e [ - 4.5,5.5 ] , сетка содержала 100 ячеек, шаг сетки составлял h — 0.1 . Эти данные аналогичны параметрам моделирования задачи в работе [1].

Шаг по времени выбирался согласно критерию Куранта-Фридриха-Леви h д tc — кс-,               (27)

c где kc – коэффициент пропорциональности (кс — 0.4863).

Для заданных параметров моделирования шаг по времени составлял _д t_c — 0.0411 .

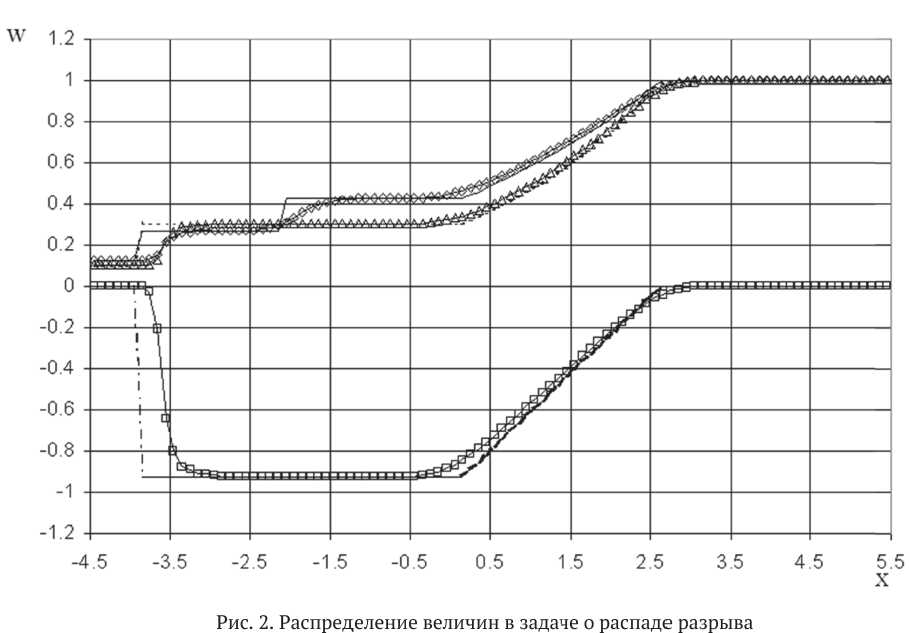
Результаты расчетов для момента времени t — 2.22583 показаны на рис. 1-3 в сравнении с точным решением Годунова [4].

Из сравнения рис. 2 и 3 следует, что модифицированная TVD схема в отличие от исходной

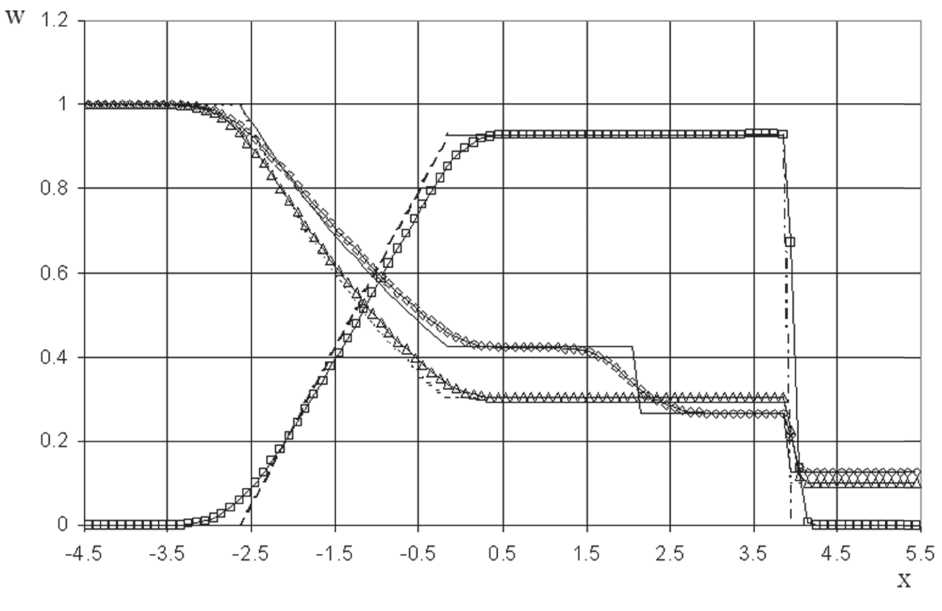
Рис. 1. Распре д еление вел и чин в зада ч е о распаде разрыва (положи т ельное направление у д арной вол н ы):

TVD схема [2] и модифиц и рованная с хема: —е-- р , —в-- и , —а --р ;

точное решение Г о дунова [4]:--р ,------и,.......- р .

(отрица т ельное нап р авление у д арной вол н ы):

Р ,

^—

TVD схема [2]: —е— точное решение Г о дунова [4]:

• -в— - и, —А--р ;

  - р ,------ и, ....... - р

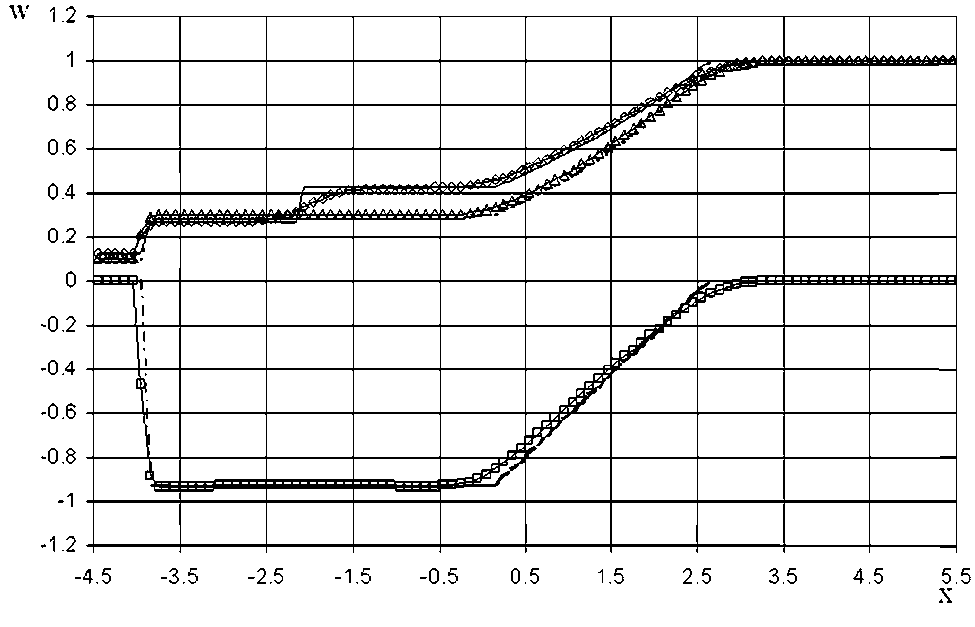
Рис. 3. Распре д еление вел и чин в зада ч е о распад е разрыва (отрица т ельное нап р авление у д арной вол н ы): модифи ц ированна я TVD схема:    о - р , —в-- и , —А-- р ;

точное решение Г о дунова [4]:-- р ,------ и, .......- р

схемы значительно повышает точность вычислений при отрицательном направлении движения ударной волны.                             1.

ВЫВОД

По численным результатам моделирования задачи о распаде разрыва можно сделать вывод, 3. что модифицированная TVD схема по сравнению с исходной схемой значительно повышает 4 точность вычислений при отрицательном на-   .

правлении движения ударной волны.