Модулярные меры и операторы Магарам

МОДУЛЯРНЫЕ ЛОКАЛЬНО ОГРАНИЧЕННЫЕ ПРОСТРАНСТВА ФЕНХЕЛЯ — ОРЛИЧА И КОНУСЫ В НИХ

В. Г. Фетисов, Н. П. Безуглова

Изучено поведение конуса, неотрицательных функций в обобщенных пространствах Ор-лича, как известно, не являющихся в полной мере метрическими пространствами при соответствующем выборе определяющей фундаментальной функции. Рассматривается ряд основных свойств конусов в векторнозначных пространствах Фенхеля — Орлича.

В работе [1] было изучено поведение конуса неотрицательных функций в обобщенных пространствах Орлича, как известно, не являющихся в полной мере метрическими пространствами (при соответствующем выборе определяющей фундаментальной функции). Здесь мы рассматриваем ряд основных свойств конусов в векторнозначных пространствах Фенхеля — Орлича (см. [2], там же содержится и обширная библиография).

1.    Основные определения и некоторые вспомогательные результаты

Допустим, что X — вещественное линейное нормированное пространство; обозначим R+ = [0,сю[ (соответственно, R⁺ = [0, сю]). Всякая функция Ф : X —> R⁺ называется функцией Орлича (в частности, если Ф — выпукла, то функцией Юнга), если Ф(0) = 0 и, если элемент х G X, х ^ в (8 — ноль пространства X), то lim Ф(Аж) = сю, где A G R.

А—» оо

Примерами функций Орлича могут служить скалярная ф-функция ФДи) = \н\^р (0 <  р < сю) (определяющая классическое пространство Лебега L_p), Х-функция Фг(и) = el^u — 1 и т. д.

Определение 1. Пусть (Q, X, д) — измеримое пространство с сг-конечной сепарабельной неатомической полной мерой р, X — линейное нормированное пространство, Ф — функция Орлича на X. Пространством Фенхеля, — Орлича L^p^X) называется множество всех таких классов эквивалентности измеримых функций и : О —> X, что существует А > 0 такое, что J Ф^ХиДр <  фею.

Можно заметить, что пространство Фенхеля — Орлича представляет собой линейное пространство.

ОПРЕДЕЛЕНИЕ 2. Функционал р : X —> R ⁺ называется модуляром [3], если выполняются условия:

• (а) <Р^ = 0) ^ (ж = 0);

• (В)    р^ = РрГ

• (с)    p^ax + Ру) < р(ж) + рру) (х, у Е X ; а, р > 0; а + р = 1).

Если условие (а) заменить условием

• (d)    /9(0) = 0,

то функционал р называется псевдомодуляром.

Пусть М — линейное пространство всех ограниченных д-измеримых функций u : Q —> X. Функционал Гф : М —> R + вида Гф = f Ф^рз^ду, есть пример интегрального модуляра на М, удовлетворяющего условиям (а)-(с).

ОПРЕДЕЛЕНИЕ 3. Пространство д-измеримых функций, определяемое интегральным модуляром Гф формулой

ЕФИ = {ж е £Ф(щХ) : lim ГФ(Аж) = 0},           (1)

называется модулярным пространством Фенхеля — Орлича.

По поводу модулярных пространств подробнее см. монографию [3].

ОПРЕДЕЛЕНИЕ 4. Функционал Ц-; Ф||, называется F-нормой, если он подчиняется условиям:

• 1.    ||и; Ф|| = 0 О и = 0 (0 — ноль пространства);

• 2.    || -щФ|| = ||щФ||;

• 3.    ||л + щФ|| < ||и;Ф|| + ||щФ||;

• 4.    если А^ ^ А и Ци^ — и; Ф|| —> 0 при к —> сю, то || А/щ^ — Au; Ф11 —> 0, к —> со. Если Ф — некоторая функция Орлича, Гф(и) — интегральный модуляр, определенный этой функцией, то с помощью формулы вида

||и;Ф|| = inf {б > 0 : ГФ (|) < б}                      (2)

можно на модулярном пространстве Фенхеля — Орлича задать Е-норму, превращающую его в Е-нормированное модулярное пространство Фенхеля — Орлича.

Определение 5. Говорят (см. [3]), что функция Орлича Ф : X —> R + подчиняется Д2- условию, если существуют постоянные к > 0 и wq такие, что Ф(2ж) < А:Ф(ж) при ||ж; Ф|| > шо и 8пр{Ф(ж) : ||ж; Ф|| = ш} < +сю.

Можно видеть, что, если функция Орлича Ф удовлетворяет Дг-условию, то класс £*^ф(щ X) совпадает с Е-нормированным пространством Фенхеля — Орлича. Отметим, что, если р — модуляр в смысле X. Накано [4], то

||и; Ф||/у = inf{a > 0 : p(u/a) < а}

есть F-норма в пространстве X с константой А > 0 в неравенстве треугольника (3), т. е. выполняется ||u + р;Ф|| < А(||и;Ф|| + ||щФ||) для любых элементов u, v е X.

Пусть X — вещественное банахово пространство. Как известно, множество К С X называется конусом, если выполнены следующие условия (см. [5]):

• (а)    множество К замкнуто;

• (б)    из w, v Е К вытекает, что aw + /3v Е К при всех а, /3 > 0;

• (в)    из каждой пары элементов х, —х по крайней мере один не принадлежит К, если х ф 0.

Всякий конус К является выпуклым множеством в X. Конус называется воспроизводящим, если каждый элемент х Е X можно представить в виде х = u — v, где u,v Е К.

По аналогии с работой [1] будем называть положительный, не обязательно линейный функционал Г(и) (u е X), обусловленный интегральным модуляром, строго растущим, если для любых un Е К (n = 1, оо), где К — конус неотрицательных функций un(s) > 0 из пространства X, из ||ип;Ф|| > с > 0 следует, / П \ что lim Г( щ ) = оо.

Лемма 1. Интегральный модуляр ГДи) = J \u(sY^Pdp, является строго растущим функционалом при каждом 0 <  р < со.

• < 1 Доказательство леммы 1 можно посмотреть в работе [1]. >

ОПРЕДЕЛЕНИЕ 6. Элемент u Е Р*(Ф, д) называется элементом с абсолютно непрерывной F-нормой, если lim ||Fr>u;D|| = 0, Pd — оператор умножения на характеристическую функцию измеримого подмножества S С Q (т. е. Pd^ = Xdu, где Xd(s) = 1, если s Е D С О и, соответственно, Xd(s) = 0, если s Е O\D).

По аналогии с нашей работой [6] можно получить следующие предложения, носящие вспомогательный характер для дальнейших построений.

Лемма 2. Функция u(s) Е £*(Ф,д) имеет абсолютно непрерывную F-норму тогда и только тогда, когда u(s) Е Е(Ф,р), где Е(Ф,р) означает замыкание в £*(Ф, д) совокупности всех ограниченных на множестве Q функций.

Лемма 3. Совокупность ЬДФ, д) всех элементов из £*(Ф, д) с абсолютно непрерывной F-нормой является сепарабельным замкнутым подпространством пространства £*(Ф, д).

Лемма 4. Если определяющая функция Орлича Ф(и) подчиняется Д2- условию, то справедливо равенство £*(Ф, д) = Е(Ф, рф

Отметим еще несколько утверждений, носящих прикладной характер в теории нелинейных операторов.

Лемма 5. Пусть дЧЧ < сю и xq Е Ь*(Ф,р). Тогда £*(Ф,ц) сепарабельно отчф^^Шф^У

• < 1 Наметим идею доказательства. Если предположить, что ЬЧФ,^ + Т^(Ф,ц), то можно указать элемент xq Е L*(Ф, ц)\£д(Ф, м), ^гД^е ж > О почти везде на ц-измеримом множестве Q. По заданной функции x₀(s) можно найти 6q > 0 и последовательность измеримых подмножеств {Q^} i^N С Q такие, что Qj П Qj = 0 и ||х^_гж₀;Ф|| > ео (в силу условия xq ^ ЬЧФ^мЧ- Обозначим через wj = ^хХп_к, где J Е N. Если наборы Ji ф J^, где Ji, J2 С N, ^kEJ .                  . . .

тогда \\wj₁ — wj₂|| >  6q. А так как {J : J С N} — несчетное множество наборов, то пространство ЬфФ, рЧ очевидным образом, является несепарабельным модулярным пространством Фенхеля — Орлича.

Обратный факт: Предполагая теперь, что А*(Ф,ц) сепарабельное модулярное пространство Фенхеля — Орлича и уп Е Ад(Ф,ц), возьмем некоторую функцию u(s) > 0, u(s) Е 5(0). Аппроксимируя ее последовательностью непрерывных функций 44neN и, используя теорему Егорова, можно с помощью аппроксимации рассмотреть произвольную функцию x(s) Е ЕЧФ, Ч и убедиться, что x(s) Е Т^ФтМ-У >

Банаховы пространства Фенхеля — Орлича достаточно полно исследованы в докторской диссертации Тюррета [2]. Что же касается модулярных пространств Фенхеля — Орлича £*(Ф,ц), определяемых вогнутыми функциями Орлича, то к настоящему времени мало что известно в этом направлении. Используя идеи работ [7] и [8], можно рассмотреть локально ограниченные модулярные пространства Фенхеля — Орлича (т. е. пространства, которые обладают ограниченной окрестностью нуля 0). Ясно, что такое пространство имеет базис окрестностей 0, состоящий из ограниченных множеств. В частности, лебеговы пространства L_p (0 <  р < сю) локально ограничены.

Лемма 6. Если ц(П) < сю л существует р > 0 такое, что lim

W—>+00

W—> + 00

Ф(шт)

-up • Ф(гс)

>0,

то модулярное пространство Фенхеля — Орлича £*(Ф, ц) будет локально ограниченным.

• < 1 Пусть выполнено условие (4) (без ограничения общности можно считать, что существует р > 0 такое, что lim „р^ф^а = сю. Тогда существует t > 1

W—>+00 U   W такое, что

W-ДОО

Ф(шт) >  и^рФ(ии)

при mw > w > to. Зададим функцию Ф следующим образом:

W) =

/ . \р ^ФМ ■ Д) , »№⁺¹) ■ (^У \ ^С0 /

если t Е [0, ^о], если ^ Е]^,^о⁺¹]

(п Е N).

Можно заметить, что Ф(£) есть функция Орлича, непрерывная при t > 0. Учитывая условие (5), при ^ <  t получим Ф(£) > Ф(£д). Кроме того, функция Ф(£) подчиняется условию

Ф(м • w) > у^р ■ Ф(гД

при mw > w > 0. Действительно, пусть Д¹< w < £g⁺¹, ^о < ^MW — ^о⁺¹>^гД^е s = п + г > п. Тогда

ф(=и > Ф1Щ¹) ■ t;^p ■ (-^у =«- ■ ФМ+¹) ■ (ДУ = «- ■ Ф(»),

Аналогично, Ф/Ф(/) <  t^p и Ф/Ф(£о) < 1, а это означает, что пространства £*(Ф,ц) и £*(Ф,ц) топологически эквивалентны. Но пространство £*(Ф,ц) является локально ограниченным. Значит, и £*(Ф,ц) — локально ограниченное пространство.

Можно заметить, что {V,, = г • В^ф(г)}_г>о образует базу окрестностей нуля 0 в модулярном пространстве £*(Ф, дУ Доказательство этого факта аналогично доказательству теоремы 3 из работы [7], и мы его не приводим. >

Лемма 7. Если ц(Г2) < сю л для всех р > 0 выполняется условие lira „р^ф^а = 0, то модулярное пространство Фенхеля — Орлича L*^,^ и—>+00 U   ™ w —>+оо не является локально ограниченным.

• < 1 Доказательство леммы 7 аналогично доказательству теоремы 7 из работы [7], поэтому мы его не приводим. >

Лемма 8. Пусть L* (Ф, ц) — модулярное пространство Фенхеля — Орлича и 0 < а < 1. Тогда для каждого элемента uq Е Ь*(Ф, дУ минорированного почти всюду на Q и для каждого подмножества С С £*(Ф, дУ удовлетворяющего соотношению lim sup \\PD (жЛ)т;Ф|| = 0,                        (7)

h^oOxEC ° существует возрастающая функция р : R —> R такая, что lim u^oo иа

= СЮ,

sup х^С

иЩ);Ф <+оо.

<1 Так как lim sup \\Pd (ж а)ж;Ф|| = 0 (вытекает из условия (7)), то су-х^°°хЕС “°  ’ ществует функция -0(A) такая, что

||-Рд„_п(_ж,А)Ж; Ф|| < 0(A), Ух Е С, где lim 0(A) = 0. ^и                                          А—7ос

Если -0(A) —> 0 при А —> сю, то существует последовательность (А_п)_пен, A_n 7 ОО

Ло = 0 такая, что ^) 0(А_П) < +сю, и также можно утверждать, что существует 71=0

некоторая возрастающая функция 5 : R  —> R , 5(A) —> сю при А —> сю,

5(A_n) = M_n Е N, Уп Е N такая, что £ М_И0(А_И_1) < оо.

Обозначим D_n^ = {s Е Q : A_n_iu₀(s) <  х^ <  A_nu₀(s)}. Пусть у>(А) = 5(A) • А^а. Ясно, что функция у>(А) возрастает. Кроме того,

^ [^] ^(s)-*|| - £ IK^ [^] н№);ф L        J                   71=1               L        J

Так как A_n 7 ^{и M}o(^s) минорирована положительным числом, то существует N_o Е N такое, что при n >  N_o выполнено x(s) > A_n_iu₀(s) > 1 почти везде на множестве D_n(xY

Отсюда можно получить оценку:

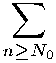
PDnwV

u0(s);Ф

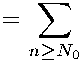
PDn(.x)5

Hs)

U0(s)

Из)|а;Ф

< E IIT_D,(,)»(A„)|_Z(_S)|«;»II <  E 11Щ,_мЛ4М»)|;Ф||

71 >  Ng                               П > Ng

• < E адРо.₀(.,л„_.)Щ);Ф||< E M„ ■ Шп-1'I < Cv n>Ng                        n>Ng

где Ci — некоторая постоянная. Аналогично оценивается часть ряда для п <

No-.

Е

H

РС,Ух^

u0(s)

u0(s);Ф

< 52 WPDn(x)

-  52 \\^PD_n(x)MN_oXNo(xn + M₀)(s); ФЦ

1 < 71 < TVq

< No • MNg • E\XNg + 1] • [||х^;ФII + 11^0; ф||] < c2, гДе C2 — некоторая постоянная. >

2. Структурные свойства конусов в модулярных пространствах Фенхеля — Орлича

Сначала мы рассмотрим вопрос о том, какие дополнительные условия гарантируют существование предела у монотонной последовательности (ж_п)пем элементов модулярного пространства Фенхеля — Орлича, полуупорядоченно-го конусом К положительных элементов. Без ограничения общности можно рассмотреть случай неубывающей последовательности x-v < х^ < ... < х_п< ... Последовательность (ж_п)пелг называется ограниченной, если существует элемент у такой, что х_п< у (Vn G N).

Существуют пространства, в которых из монотонности и ограниченности (x_n)_nEN вытекает сходимость по F-норме. Например, если пространство X = L_p упорядочено при помощи конуса неотрицательных функций, то для каждой неубывающей ограниченной последовательности (x_n)_nEN функция x*(s) = supx_n(s) (s G Q) также принадлежит L_p.

Пространство, в котором каждая ограниченная монотонная последовательность имеет предел, будем называть в дальнейшем правильно упорядоченным. Соответственно, конус К, который порождает правильную упорядоченность в пространстве, будем называть правильным. Последовательность (x_n)_nEN ограничена по F-норме, если ||ж_п;Ф|| < М, где М G R. Наконец, конус К назовем вполне правильным, если каждая монотонная ограниченная по F-норме последовательность (x_n)_nEN сходится по F-норме к некоторому пределу.

Теорема 9. Пусть на конусе К неотрицательных функций из модулярного пространства Фенхеля — Орлича £*(Ф, ц) определен строго растущий и ограниченный на каждом шаре в пространстве £*(Ф, ц) функционал Г (и), тогда конус К обладает свойством вполне правильности.

• <1 Предположим противное. Тогда найдется такая расходящаяся по F-норме (2) последовательность элементов (w_n)_nEN G К такая, что

  
  

W1 < W2 < ... < Wn < ...

Будем считать для определенности, что ||wi; Ф|| > бо, |Н^+1 — гсдФЦ > бо > 0 (г = 1, оо), так как в противном случае всегда можно перейти к подпос ледовательности (wnk) в £*(Ф,ц), обладающей указанным свойством. Тогда

П —1

lim Г(гс_п) = П—УОО

lim Г wi + 52 (Wi-H - wd t^oo L      i=i

= оо, а это уже противоречит огра

ниченности функционала Г(и) на шаре ||щФ|| < М. Отсюда вытекает, что последовательность (wn)nEN G К сходится по F-норме (2) и, значит, конус К обладает свойством вполне правильности. >

Следствие 10. Конус К неотрицательных функций из р-однородного модулярного пространства Ь_Р(П) (0 < р< сю) обладает свойством вполне правильности.

Теорема 11. Пусть на конусе К неотрицательных функций из модулярного пространства Фенхеля — Орлича £*(Ф, д) определен монотонный строго растущий функционал. Тогда конус К обладает свойством правильности.

• <1 Доказательство аналогично доказательству теоремы 9, предоставляем провести его читателю. >