Молекулярная динамика процесса адиабатного расширения

Математическое моделирование и оптимальное численное решение дифференциальных уравнений первого и второго порядка, описывающих процессы происходящие в молекулярных системах, позволяют прогнозировать свойства известных и вновь синтезируемых материалов в труднодоступных для натурного эксперимента условиях, в которых поведение свойств вещества малоизученно.

Существует ряд программных продуктов позволяющих моделировать молекулярные системы в равновесных состояниях. Однако, эти программные продукты применимы для моделирования состояний с заданными термодинамическими параметрами (ансамблей) и малопригодны для имитации термодинамических процессов (охлаждение, прессование, расширение).

Довольно широко применимо моделирование процесса изохорного охлаждения [1, 2]. Нами была предложена и апробирована методика моделирования процесса изобарного охлаждения [3].

Остается открытым вопрос создания методики проведения имитационного моделирования процесса адиабатического расширения, позволяющих детально прослеживать динамику таких свойств как адиабатическая сжимаемость, скорость звука.

1. Классическая молекулярная динамика

Уравнения движения частиц молекулярной системы определяются из формы потенциала взаимодействия

m

d² Г ( t ) dtt

N -1

Т ^{Х Ф} ( r j ) ,

где m - масса частицы, r - радиус вектор частицы. Для системы инертных частиц хорошо подходит модель взаимодействия, предложенная Леннар дом-Джонсом:

Ф ( Г ) = 4 s

—

где е - глубина потенциальной ямы, а - эффективный размер частицы.

Система дифференциальных уравнений (1) при значительном количестве частиц аналитически нерешаема, поэтому для расчета траекторий движения прибегают к численному интегрированию. Для этого разложим векторы положения частиц в моменты времени t+ A t и t- A t в ряд Тейлора: r( t + A t ) = r( t ) +

d r( t + A t) dt

A t + 1 r ⁽ t ^{+ A} t )

A t > 0

a t ²

A t > 0

a 1 2 + 1      ^{t +} ' ^{t :}

dt

A t ³ +O ( A 1 ⁴),⁽³⁾

A t > 0

r( t — A t ) = r( t ) — d r ( t + A t )

—

d t

,    1 d2 r( t + A t)

A t +--Ц---

A t > 0       2      d t ²

A t > 0

A t2

—

1 a ³ r ( t +a t )

6 d t ³

A t ³ +O ( A 1 ⁴).⁽⁴⁾

A t > 0

Складывая выражения (3) и (4), получим основное уравнение метода численного интегрирования Верле [4]

r ( t + A t ) = 2 r ( t ) — r ( t — A t ) + ( t )A t²+O(A t⁴),               (5)

d2Г где д(t) = — - ускорение частицы, определяемое из (1). Метод интегри-dt2

рования описываемый выражением (5) несколько неудобен, так как для начальной реализации его необходимо получение нескольких точек коор- динат с использованием других методов численного интегрирования.

Вычитая (3) из (4) выразим скорость v (t)

_v( _t ) = d r ( t ) = ^{r (} t ^{+ A} t ) ^{— r (} t ^{— A} t )

¹      dt              2 A t         •

Таким же образом получим выражение для скорости на момент време-ни t+^t :

. х _ r ( t + 2 A t ) - r ( t ) _ 2 r ( t + A t ) - r ( t ) + a ( t + A t ) A t ² - r ( t )

v(1 + 1) =     2A =              2A

r ( t + A t ) - r ( t ) A t

+ ^a ( t + A t ) A t

rxx rxx      1

r ( t ) + v ( t ) A t + — a ( t ) A t ² -

A t

r ( t )    1               _      1

----+ —a ( t + A t ) = r ( t ) +—[ a ( t ) + a ( t + A t ) ] A t .

Выражения (3) и (7) в совокупности представляют алгоритм Верле в скоростной форме для численного интегрирования уравнений движения [5].

В отсутствие внешних сил система частиц приходит к термодинамическому равновесию с заданными температурой, плотностью и давлением.

система после расширения для выполнения условия постоянства энтро-

пии. В свою очередь давление P 2 определяется из теоремы о вириале

/

^P 2 = Р ² <  E

v

, *     1 N-V 5Ф i к2 > ЛГ<^^ Г Л >1 .

^N -= 1 j >  - ⁵ r J

Подставив (9) в (8), выразим < Ek 2 > и затем произведем нормировку < Ek2 > / < Ek2 >, соответствующий нормировочный коэффициент для ско- k =

ростей частиц системы определится выражением

A dV \ 1/   \ 2/      2

Sр\ - Р_!уУФ Ф J ; 17 3 ^ \j j i1 a^ /J

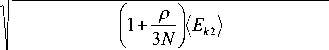
• 5.    Повторяем пункты 1-4 до установления необходимого объема.

Фазовая траектория участков усреднения (пункт 3), последующих непосредственно после актов изменения объема, будет отлична от траектории адиабатического процесса, но дискретные состояния после корректировки кинетической энергии будут соответствовать адиабате.

Стоит отметить, что данная методика пригодна для моделирования медленного расширения, так как в случае больших значений dV выражение (8) перестает отвечать требованиям корректности численного интег- рирования.

Метод моделирования процесса адиабатного расширения открывает возможности численного расчета адиабатической сжимаемости , которую очень трудно измерить на практике

P s =-

1 ( dV )

VI dP J S"

• 3. Апробация

Предложенный метод моделирования реализован в программном комплексе MDDx11 [6].

В целях апробации методики была произведена инициализация систем из 1000 частиц аргона ( s/k=119.8 К, o =3.405 А) в различных температурных точках изобары со значением давления 4 МПа. Для полученного набора стартовых конфигураций была проведена серия компьютерных экспериментов, моделирующих процессы адиабатного расширения с изменением плотности 0,5 % от плотности стартовой фазовой точки. Значения удельных объемов начальных конфигураций, значения удельных объемов, полученные в результате расширения и соответствующие значения давления подставлялись в выражение (11) для вычисления e S . Рассчитан -ные по результатам компьютерного моделирования значения адиабатической сжимаемости представлены на рис. 1.

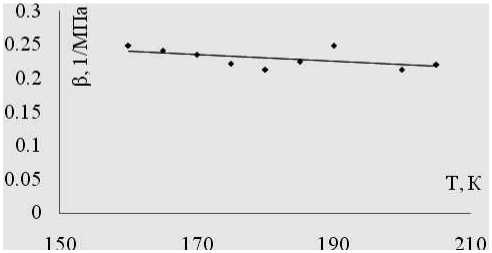
Рис. 1. Адиабатическая сжимаемость аргона при давлении 4 МПа по данным компьютерных экспериментов, моделирующих адиабатическое расширение в окрестностях фазовых точек изобары

Полученные результаты хорошо согласуются с литературными данными [7].

Заключение

Предложена методика компьютерного моделирования процесса адиабатного расширения молекулярных систем. На моделях систем частиц аргона произведена апробация методики и получены значения адиабатической сжимаемости. Методика моделирования физически обоснована, а результаты апробации хорошо согласуются с литературными данными.