Молекулярно-динамическое моделирование структуры и свойств стеклообразной подложки SiO2 в широком диапазоне температур

Как известно, в микроэлектронике в качестве подложек для нанесения тонких пленок и интегральных микросхем широко используют аморфные подложки из чистого оксида кремния SiO 2 . Такие подложки имеют очень низкий коэффициент линейного расширения, высокую стойкость к тепловым импульсам и химическую стойкость. Кроме того, граница раздела Si/SiO₂ считается важным элементом в устройствах металл–оксид–полупроводник. Таким образом, для разработки современных наноэлектронных устройств становится важным качественное моделирование аморфной системы SiO₂ на атомном уровне.

Получение прямых данных о деталях атомного строения аморфных систем требует проведения дорогостоящих и ресурсоёмких исследований. Альтернативой может служить сочетание доступных экспериментальных данных с изучением структуры стекол методами молекулярной динамики. Однако для моделирования системы в пространственных и временных масштабах, представляющих интерес для инженерных приложений (несколько сотен тысяч частиц во временном интервале порядка наносекунд), возможно использование только классической молекулярной динамики с эмпирическими потенциалами межчастичного взаимодействия, параметры которых выбираются на основе доступных экспериментальных данных. Однако, следует иметь в виду, что вязкость и температура стеклования кварцевого стекла существенно зависит от исходных материалов, способа производства, состава и количества примесей [1].

К настоящему времени для анализа структур SiO₂ использовался целый ряд потенциалов [2– 9], которые позволяют рассчитать структурные свойства различных полиморфных модификаций кварца в неплохом согласии с экспериментальными данными и результатами ab initio расчетов. Потенциальная энергия системы представляется в виде суммы слагаемых, описывающих электростатическое взаимодействие и взаимодействие Ван-дер-Ваальса. Как правило, первое слагаемое рассчитывается в приближении кулоновского взаимодействия точечных зарядов, центрированных на атомах. Для описания взаимодействия Ван-дер-Ваальса используются как парные потенциалы [1–6], так и трехчастичные потенциалы Стилинджера–Вебера и Вашишты [8, 9]. Поскольку в дальнейшем мы планируем изучать процессы нанесения пленочных покрытий для моделей толщиной до 100 нм, содержащих несколько миллионов атомов, то сложные трехчастичные потенциалы не могут использоваться по причине высокой времязатратности.

Физика

Наиболее популярный двухчастичный потенциал BKS (Van Beest, Kramer, van Santen [4]), в котором взаимодействие Ван-дер-Ваальса описывается потенциалом Букингема, обладает существенным недостатком, препятствующим его использованию для моделирования процессов напыления тонких пленок на поверхность кварцевого стекла. Недостаток состоит в том, что при малых расстояниях потенциал Букингема имеет нефизическое поведение, связанное с резким возрастанием слагаемого, обратно пропорционального шестой степени расстояния. Экспоненциальный член не может компенсировать этот рост, в результате чего потенциал имеет нефизическую область притяжения на малых расстояниях между частицами [10]. Поскольку при моделировании напыления столкновения между частицами достаточно часто приводят к такому сближению, то может наблюдаться артефакт взаимного захвата частиц, искажающий результаты моделирования. Поэтому для моделирования аморфного кварца в данной работе использован потенциал DESIL, предложенный в работе [2] и лишенный данного недостатка. Кроме того, двухчастичный потенциал DESIL позволяет проводить более длительные прогоны и, таким образом, изучать равновесные свойства системы при более низких температурах или исследовать стекла с более низкой температурой стеклования.

Цель настоящей статьи двояка. Во-первых, мы хотим проверить, может ли выбранный нами двухчастичный потенциал, воспроизводить структурные свойства аморфного кремнезема. Во-вторых, мы хотим подобрать методику моделирования аморфного стеклообразного кремния (влияние начального состояния, скорость изменения температуры) для получения модели стекла, согласующейся с данными эксперимента.

Методика моделирования

Функциональная форма потенциала DESIL [1] задается суммой кулоновского члена и потенциала Леннард-Джонса. Таким образом, потенциал между частицей i и j определяется выражением:

U= ^qiqj +4ε ij r_ij

”у г. ■Г- ■

V r ij 7 V r ij 7

где q_i , q _j – заряды взаимодействующих атомов, r_ij – расстояние между атомами, σ_ij – расстояние нулевой энергии взаимодействия, ε_ij – глубина потенциальной ямы. Используемые значения параметров приведены в табл. 1.

Таблица 1

i-j	C 12 , кДж∙нм12/моль	C 6 , кДж∙нм6/моль	Атомный заряд, e
Si-O	4,6∙10–8	4,2∙10–3	1,30 (Si)
O-O	1,5∙10–6	5,0∙10–5
			–0,65 (O)
Si-Si	1,5∙10–6	5,0∙10–5

МД-расчеты проводились с использованием кода LAMMPS (Sandia National Labs, US). Уравнения движения интегрировались с помощью алгоритма Верле c временным шагом в 1 фемтосекунду.

Дальнедействующие кулоновские взаимодействия учитываются с помощью суммы Эвальда (точность вычислений 10^–5) с расстоянием отсечки r cut =10 Å. Для приемлемого компромисса между точностью и объемом вычислений был выбран размер системы порядка 500 атомов (см. далее). Расчеты проводились при нулевом давлении для сравнения с экспериментальными данными, измеренными при атмосферном давлении. Грани кристалла при этом варьировались независимо.

Модель аморфного кварца была получена методом закалки из высокотемпературного расплава. На протяжении всего моделирования использовался термостат Нозье–Гувера в изотерми-чески-изобарической форме (NPT). В качестве начальной структуры был взят альфа-кварц, 64 элементарные ячейки которого использовались в качестве ячейки моделирования с периодическими граничными условиями. Общее число частиц в ячейке моделирования составляло 576 атомов (192 атома кремния, 384 атома кислорода).

Для получения амфорной модификации кристалл нагревался со 100 К до 2700 К, выдерживался при достижении высшей температурной точки, охлаждался и вновь выдерживался при достижении конечной температуры 100 К (скорость нагрева равна 1 К/пс, скорость охлаждения 10-2 К/пс). Для определения равновесных параметров для различных температур температурных шагов производились выдержки в течение 100 пс при каждом изменении температуры на 100 К. Выдержки при максимальной температуре (выше температуры плавления), начальной и конечной температурах были больше и составляли 1 нс.

В качестве начального состояния системы использовалась кристаллическая структура альфа-кварца (64 элементарные ячейки, 576 атомов) с плотностью 2,66 г/см³, соотношением граней a / c= 1.10, длинами связи Si-O = 1,62 Å, O-O = 2,64 Å и углами связей O-Si-O = 108,3°, Si-O-Si = 143,1°. После начала моделирования в течение нескольких пикосекунд наблюдаются значительные колебания плотности (с амплитудой примерно 0,25–0,35), которые со временем затухают (полностью – примерно через 30 пс), после чего плотность системы стабилизируется при значении ρ = 2,33 г/см³. При этом атомы совершают своеобразные групповые колебания, приводящие к некоторому изменению исходной структуры. Скорее всего, релаксация связана с тем, что структура альфа-кварца не соответствует минимуму потенциальной энергии для используемого потенциала DESIL, поэтому происходит релаксация к структуре с более низкой энергией. Полученная конфигурация в дальнейшем будет приниматься за начальную низкотемпературную (100 K) структуру.

Моделирование также осуществлялось с начальным состоянием системы в виде кристаллической структуры бета-кварца с плотностью ρ = 2,53 г/см³, соотношением граней a / c = 0,92, длинами связи Si-O = 1,57 Å, O-O = 2,56 Å и углами связей O-Si-O = 109,8 , Si-O-Si = 155,4 . Как и в первом случае, после запуска моделирования происходит релаксация, по результатам которой получается описанная выше начальная низкотемпературная (100 К) структура. Кроме того, параметры полученной методом закалки аморфной фазы полностью идентичны результатам, полученным с использованием структуры альфа-кварца: функции распределения практически полностью повторяются, тепловой коэффициент расширения качественно схож, а конечная плотность кристалла отличается лишь на 0,03 г/см³. Таким образом, независимо от выбранного начального состояния результат фактически был одинаков.

Результаты моделирования

По результатам моделирования были построены зависимости усреднённых значений плотности системы от температуры при нагревании начальной структуры до температуры 2700 К, значительно превышающей температуру плавления, затем при последующей закалке, в результате которой формируется аморфная фаза, и при повторном нагреве данной фазы (рис. 1).

Температурная зависимость плотности при нагреве начальной структуры качественно очень похожа на экспериментальную для силикатного стекла типа I [11]. Действительно, при температуре порядка –70 °С наблюдается небольшой минимум плотности, после чего кривая возрастает, достигая максимума приблизительно при 1700 °С. После этого плотность начинает монотонно снижаться, а при температуре 2500 К система плавится, что приводит к резкому понижению плотности примерно, до 2,0 г/см³, что неплохо согласуется с экспериментальным значением порядка 2,1 г/см³ [12]. При закалке из расплава плотность системы изменяется немонотонно и при температуре 100 К достигает значение 2,21 г/см³, что находится в хорошем согласии с экспериментально наблюдаемым значением 2,20 г/см³ [11] для чистого кварцевого стекла. Следует понимать, что в силу использования периодических граничных условий полученную нами модель аморфного стекла следует рассматривать как структуру отдельного микрокристаллита, являющегося основой кварцевого стекла. Аморфная структура стекла образуется путем объединения случайно ориентированных микрокристаллитов и небольших областей межкристаллитных границ, близких по строению к расплаву SiO 2 .

Изменение функции радиального распределения (ФРР) в процессе получения аморфного кварца методом закалки (включая область высоких температур) приведено на рис. 2. График содержит сравнение данных для альфа-кварца, структура которого использовалась при запуске моделирования, начальной низкотемпературной (100 К) структуры, образовавшейся в результате релаксации структуры альфа-кварца, и аморфной структуры, полученной в результате охлаждения до 100 К высокотемпературного расплава.

Физика

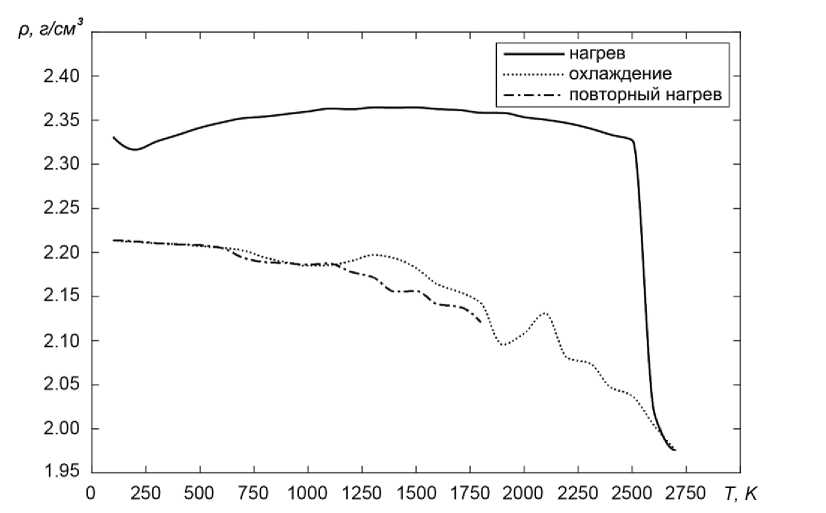
Рис. 1. Изменение плотности SiO 2 в процессе моделирования

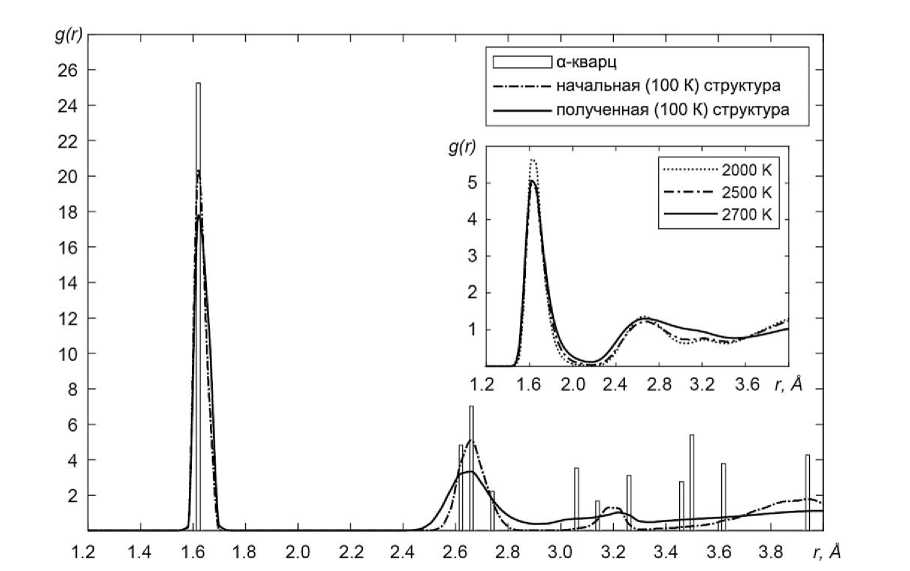
Рис. 2. Изменение функции радиального распределения (ФРР) SiO 2 в процессе получения аморфной фазы методом закалки

Видно, что ФРР для структуры, полученной методом закалки из расплавленного кварца (аморфной фазы), имеет существенно большее уширение пиков. Чтобы подтвердить, что полученная нами структура действительно является аморфной, было проведено сравнение ФРР с данными эксперимента по дифракции нейтронов для плавленого кварца [13]. Как видно из рис. 3 наблюдается хорошее согласие полученной при моделировании аморфной структуры с высокоточным экспериментом.

Черновол П.И., Мирзоев А.А.

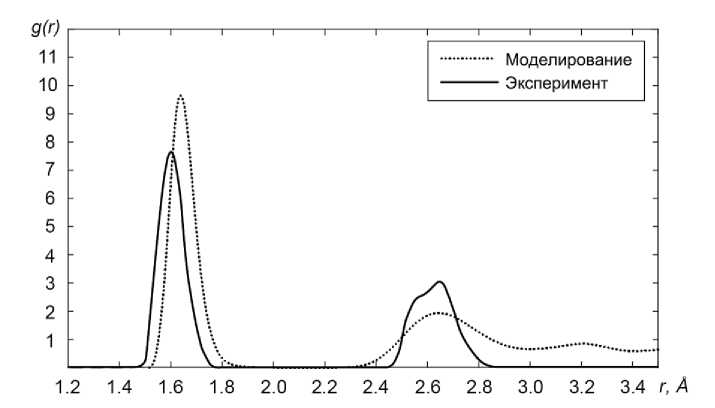
Рис. 3. Сравнение функции радиального распределения полученной аморфной фазы с экспериментальными данными по дифракции нейтронов на образцах плавленого кварца для температуры 900 К [13]

На рис. 4 приведено распределение углов связи (O-Si-O и Si-O-Si ) для начальной и аморфи-зированной структуры, а также для ряда высоких температур при нагревании в сравнении со структурой α-кварца.

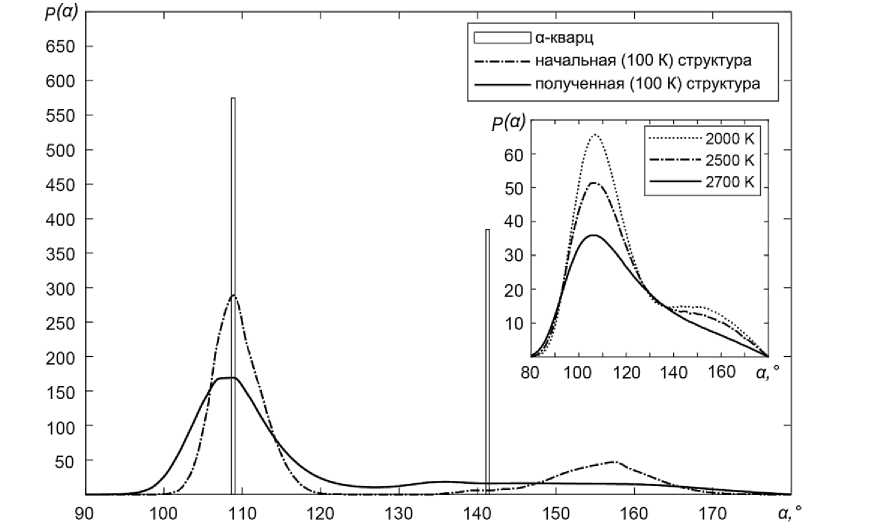
Рис. 4. Изменение функции распределения p(α) углов связи в молекуле SiO 2 в процессе получения аморфной фазы методом закалки

По окончании процедуры закалки среднее значение угла O-Si-O для модели плавленого кварца составляет порядка 108,9–110,7°. Основной структурной единицей по-прежнему является тетраэдр. Сравнение средних значений длин связи построенной модели с экспериментальными данными [13] приведено в табл. 2. Заметное отличие наблюдается только для длины связи Si-Si, для пар Si-O, O-O значения идентичны.

Физика

Таблица 2

	Si-O, Å	O-O, Å	Si-Si, Å
Моделирование	1,63	2,64	3,22
Эксперимент	1,61	2,63	3,08

Полученная аморфная фаза повторно нагревалась со 100 К до 1800 К (с прежней методикой нагрева, включая выдержки) с целью определения коэффициента линейного теплового расширения (рис. 5).

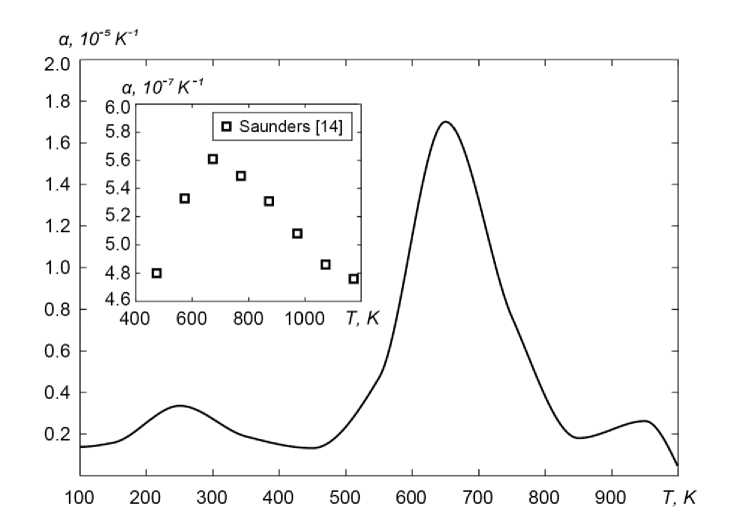
Рис. 5. Значение коэффициента линейного теплового расширения в широком диапазоне температур

Коэффициент линейного теплового расширения полученного кристалла в диапазоне от 100 К до 1000 К в среднем составляет 5,0×10–6 К–1, что почти на порядок выше среднего экспериментального значения 5,4×10–7 К–1 [14] для данного диапазона температур. Однако этому расхождению не следует удивляться. Как мы уже отмечали выше, наша модель является локальной и относится к микрокристаллитному образованию, тогда как тепловой коэффициент линейного расширения (ТКЛР), измеренный методами дилатометрии, является макроскопическим. Низкое значение дилатометрического ТКЛР связано с наличием в макроструктуре структурных особенностей, которые с ростом температуры могут сокращаться, компенсируя более высокие значения локальных ТКЛР [13]. Значительно более важным является качественное согласие температурной зависимости теплового расширения в нашей модели с экспериментальными данными, приведенными на вставке рис. 5.

Выводы

В рамках настоящей работы проведена расширенная демонстрация возможностей простого парного потенциала DESIL [1] для предсказания структурных и термодинамических характеристик аморфных силикатных стекол. Подобрана методика моделирования аморфного стеклообразного кремния. Показано, что данный потенциал вполне удовлетворительно воспроизводит плотность, функцию радиального распределения и температурную зависимость коэффициента термического расширения аморфного кремнезема в широком диапазоне температур.

Черновол П.И., Мирзоев А.А.