Momentum Based Level Set Method For Accurate Object Tracking

Published Online December 2010 in MECS

Object tracking is a crucial task within the computer vision field. It has been widely applied in applications such as video surveillance [1], perceptual user interface [2], video coding [3] and driver assistance [4]. Various tracking algorithms have been proposed in these years [510], for ease of discussion, which are divided into two categories [6,10], namely, region-based method and contour-based method.

The basic idea of region-based method is to track object with the similarity measure of object region. The most widely used similarity measures include the Bhattacharyya coefficient [11-13], Kullback–Leibler divergence [12,14] and so on, and the mean-shift algorithm in which uses Bhattacharyya coefficient has achieved considerable success in image segmentation and tracking [15-19], for its simplicity and robustness. The real-time kernel-based object tracking proposed by Comaniciu [15] can successfully track partial occluded nonrigid objects, but cannot cope with the deformation of object contours and will cause the serious bias when similar colors exist nearby. A more discriminative similarity measure in spatial-feature space was proposed by Yang [20], which can effectively cope with the translation and scaling of the object, but does not consider the rotation invariance. During a visual tracking process, the scale of the tracked target may continuously vary. In order to achieve precise localization, the target scale or the kernel bandwidth must be adaptive. Numerous methods have been developed for adaptive adjustments of the target scale. Comaniciu et al. [16] proposed to apply the mean-shift procedure three times with three different kernel bandwidths derived by adding or reducing 10 percent of the current target size during each repetition, from which the optimal scale with the maximum Bhattacharyya coefficient will be selected. A data-driven scale selection method was presented in Refs. [21,22]. By analyzing the local statistical characteristics around each data point, the kernel bandwidth is calculated. Collins developed a scheme for blob tracking over the scale space [23]. A scale space mean-shift procedure is first executed and then the spatial space calculation is processed over multiple scales. But all of the scale updating methods cannot solve the object deformation very effectively.

For contour-based methods, Algorithm can be performed using two different approaches. The first approach uses state space models to model the contour shape and motion. The second approach directly evolves the contour by minimizing the contour energy using direct minimization techniques such as gradient descent. Terzopoulos and Szeliski in 1992 define the object state by the dynamics of the control points, which modeled in terms of a spring model moving the control points based on the spring stiffness parameters. Chen et al. in 2001 propose a contour tracker where the contour is parameterized as an ellipse, in which each contour node has an associated HMM and the states of each HMM is defined by the points lying on the lines normal to the contour control point. While another approach, Yilmaz [24] incorporated prior shape into object energy functions, and used level set to evolve the contour by minimizing the energy functional. Chung and Chen [25] presented a video segmentation system that integrated Markov random field (MRF)-based contour tracking with graphcut image segmentation. Contour-based methods can achieve a high tracking precision, but their robustness is usually not better than that of region-based methods. Furthermore, the computing cost of contour-based methods is usually high, especially for large and fastmoving objects.

Combining the merits of region-based and contourbased methods, we introduce a robust object tracking method. First, the PPM is adopted to locate the object region, and the Kalman filter is used to determine the initial object tracking position. Then the object feature image is generated after a series of pre-processing, and the momentum based level set segmentation is used to evolve the object contour in order to improve the tracking precision.

The paper will proceed as follows. In Section II, we describe the idea of target prediction with the Kalman filter and rough object localization with PPM. Then, Section III presents how to evolve the object contour in the object feature space with the momentum based level set segmentation. This method will be tested and verified in Section IV, and simultaneously we will give out our results of experiments. Finally, Section V concludes the paper and presents ideas for our future work.

• II.    T ARGET L OCALIZATION

• A.    Target Prediction Based on the Kalman Filter

  The Kalman filter was proposed by R.E. Kalman with his famous paper in 1960, describing a recursive solution to the discrete-data linear filtering problem. It consists of a set of mathematical equations that provides an efficient computational means to estimate the state of a process, in a way that minimizes the mean of the squared error. The filter is very useful in three aspects: estimations of past, present, and even future states. In this paper, we use the Kalman filter to predict the center [ x ₀ , y ₀ ] of the object region before beginning to track. Let v_x and v_y represent the velocities in the x and y directions, respectively, and the state vector can be represented as x = [ x 0 , У 0 , v_x , v_y ]. Therefore the system can be modeled as

xt+i = фХ + w.

The measurement model in the form needed by the Kalman filter is z. = Hxt + vt.

where

" 10 T 0 "

0  10 T         Г1  0 001

Ф =                , H =

0 0 10          ^0  1  00

0 0 0 1

Given the state model in (1) and measurement model in (2) as well as some initial conditions, the state vector x t _{+ 1} can be updated using the system model (for prediction) and measurement model (for updating).More details about the Kalman filter can refer to [26] and [27].

• B.    Object Tracking with the PPM

Image matching is an important part for visual tracking, and the Bhattacharyya coefficient usually is an efficient method. But since the influence of background feature, the optimal location obtained by Bhattacharyya coefficient may not be the exact target location. Thus, biased or even wrong location may occur in visual tracking. Taking into account the statistical features of a search region, PPM can decrease the interference of the background pixels enclosed in the model, highlight the significant target features, at the same time reduce the influence of the features shared by both the target and the background, and exhibit an excellent monotonic property and a distinct peak-like distribution [19].

The aim of image matching is to search locally for a sub-area within an image which is most similar to a predefined target model. The sub-areas to be matched against the target model is called target candidate. To reduce the computational cost, m u -bin histograms are used. Thus, we have the target model q = { q u } _u = 1 m and the target candidate p = { p u } _u = 1 m u . Assuming 5 is the un-normalized histogram vector of the search region, PPM which is an evaluation of the posterior probability of a target candidate to be identified as the target can be defined as

Ф ( p , q ) = —^^- p u q u m u = 1 ⁵u

.

where s_u , p_u , and q_u represent the u th elements of the un-normalized histogram vectors s , p , and q , respectively; m is the number of pixels in the target model, which is a normalization constant.

Equation (3) can be transformed to the pixel-wise form:

Ф ( P , q ) = - E q u ( j )

, m j=1 5u (j)

.

where j is the pixel index, q_u ( j ) and s_u ( j ) represent the u th bin value of the target model histogram and the search region histogram, respectively. Obviously, we can regard the value of q_u ( j ) s_u ( j ) as the contribution of pixel j to the similarity value. Thus, the PPM can be computed by accumulating individual pixel’s contributions.

The pixel-wise PPM in (4) creates conditions for scale adaptation because it is simply a linear combination of contributions from individual pixels. So the PPM can be averaged to obtain an approximate contribution of each pixel to the similarity measure as ф = ф( p(y *), q) m

where y ^* denotes the current target center position. The average similarity contributions of the pixels in the inner and outer layers are denoted as

ф _:,i — - a ,...,0,..., a .                                            (6)

where i <  0 means the i th inner layer, i >  0 means the i th outer layer, and i — 0 represents the target region border.

An empirical scale adaptation formula is given as where C is a 1D curve embedded in a 2D domain, Qc is the inside region of C , f (x, y) is a scalar function called cost function and a is a regularization weight parameter.

Translating (8) to a level set partial differential equation (PDE) so we acquire a familiar level set equation:

и < k ) + 2

w ( k + 1) — <

и < k ) - 2

if ф_{- 1} >  0.8 and ф ₀ >  0.75 and ф >  0.6

if ф ₀ <  0.6 and ф <  0.3

w ( k )     else

^ ^{— -} f ⁽ x , y ) |^{v ф} | ^{+ a} ^ ^{v ф} .          ⁽⁹⁾

where к is the curvature of the contour.

Turning to gradient descent with momentum, a search direction is chosen according to:

where w ( k ) is the size of the target region at frame k .

The detailed object localization and scale adaptation process with PPM was introduced in [28].

S k ^{— -} П (1 ^{- o )v} f_k ⁺ ® S k - i ■              ⁽¹⁰⁾

where n is the learning rate and о e [0,1] represents the momentum.

• III.    E VOLUTION OF O BJECT C ONTOUR

After the target localization with the PPM, the object feature image is generated after a series of pre-processing such as background subtraction or using the color probability density information in the object region. Then we adopt the momentum based level set segmentation to evolve the object contour in the object feature space, in order to improve the tracking precision.

• A.    The Momentum Based Level Set Segmentation

Level set method was proposed by Osher and Sethian, which can compatibly solve the problem of arbitrary topology change. To improve the convergence and the search speed, while reaching the global optima as fast as possible, in this paper, we use a momentum based level set segmentation method by simulating the physical properties of inertia and momentum and effectively allowing the search to avoid local optima and accelerating in favorable directions [29]. It has employed a simple energy functional based on a weighted region term combined with a penalty on curve length for regularization. Obviously, our goal is to maximize:

E ( C ) — JJ _q f ( x , y ) dxdy - a j C ds .         (8)

The difference between two subsequent time instances of the level set function is taken to approximate the direction of the gradient, and the entire level set function can be represented as one vector:

v f ( t n ) . ^фt - ) ^{- ф} t n - 1 ) A t

.

Note that this is really an approximation, depending on the time interval between two adjacent points A t — t n - t n _{- 1} . Therefore we update the level set function with a momentum term:

ˆ

s ( t - ) —- n (1 - о ) ^{ф (} t^- ) - ^{ф (} t^{- -} ^ + ® s ( t - - 1 ).       (12)

A t

ф ( t - ) — ф ( t - - 1 ) + A ts ( t - ).                 (13)

The procedure of Update Level set is:

• •    Step1: Given the level set function ф ( t_- _ ₁) , the next intermediate time step ф ( t_- ) can be computed according to (9).

• •    Step2: Compute the approximate gradient by (11).

• •    Step3: Compute a step s ( t_- ) according to (12).

  

  Figure 1. Tracking of the ice hockey sequence with the kernel-based method (top) and our method (bottom). Frames 1, 6, 13, 21, and 37 are shown.

  
  
  

  Figure 2. Tracking of the vehicle1 sequence with the kernel-based method (top) and our method (bottom). Frames 1, 9, 19, and 23 are shown.

  
  
  

  Figure 3. Tracking of the vehicle2 sequence with the kernel-based method (top) and our method (bottom). Frames 1, 10, 30,and 37 are show.

  
  

• •    Step4: Compute the next time step φ ( t_n ) by (13) and the intermediate level set function computed in Step 1 will be replaced.

• B.    Evolution Control

We define the convergence condition as ∇ f _∞<  0.03 , with ∇ f given in (13). If the convergence condition is satisfied, iteration stops, otherwise, iteration continues.

• IV.    E XPERIMENTAL R ESULTS AND D ISCUSSION

In order to test and verify the effectiveness of proposed algorithm, we did some experiments of videos, and have implemented our idea with Matlab7.0.1 on

Windows Xp, AMD Athlon(tm) 64 X2 Dual Core CPU, 1.9GHz, 2GB RAM.

Fig. 1 shows the tracking results of the ice hockey sequence with the kernel-based method [15] and our method, in which the frames with deformation are shown. The ice hockey sequence has 40 frames of 240 x 320 pixels. The scale of the kernel is adjusted with ± 10% of the current size. The color spaces for our method and the kernel-based method are both quantized into 16 x 16 x 16 bins. Fig. 2 and Fig. 3 show the tracking results of two vehicle sequences that obtained by ourselves with the kernel-based method [15] and our method, which has 28 frames of 576 x 704 pixels and 37 frames of 576 x 704 pixels, respectively. The first frames are all the manual initialization, in which we can see that a higher precision target template is obtained with contour segmentation algorithm, eliminating the background interference in a way. In Fig. 1, because of background pixels included in target template and deformation of the athlete while fast moving, a bias occurs in frame 13. As for two vehicle sequences, since the traffic system usually track the vehicles for some time to get useful information like velocity, licensing information and so on, we just select a certain drive distance to track. The environment of the road becomes more complex than the ice hockey sequence, so the difficulty of the tracking task is higher. In Fig. 2, the kernel-based method has a bias through the sequence and the bias becomes more obvious when a motorcycle appears from the back of the target, while our method performs very well. In Fig. 3, the kernel-based method maintains a distinct bias owing to the similarity of the colour between the road and the target.

In order to evaluate the tracking precision quantitatively, we adopt the error measure as follows:

( O ∩ O ) ∪ ( B ∩ B )

error = 1 - ^{1     2       1     2} .          (14)

O ₁ ∪ B ₁

where O ₁ and B ₁ are the object region and background region in the manual segmentation result, O ₂ and B ₂ are the object region and background region in the segmentation result with the object tracking method. Meanwhile, the location error of object center is adopted to evaluate the location precision, which is defined as follows:

d =II C_a - C_m II .                    (15)

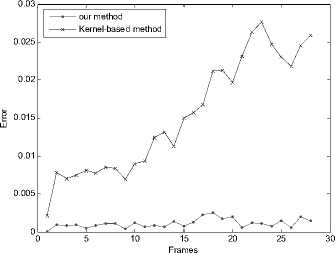
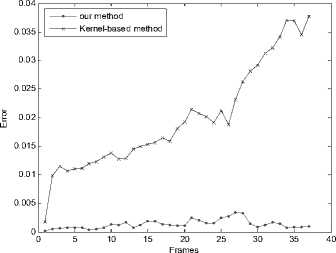
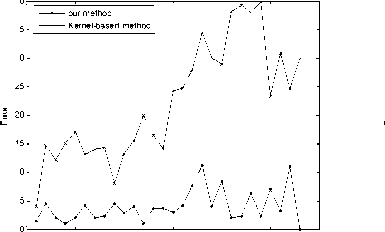
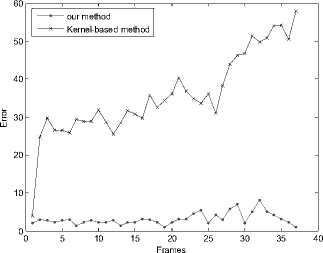
where C _a and C_m are the object center coordinates of the object tracking and manual segmentation results, respectively. Fig. 4 which shows the tracking errors of Figs. 2 and 3, respectively, indicates that our method can cope with the deformation and the scale change more effectively than the kernel-based method, so our method can achieve a higher tracking precision. Fig. 5 which shows the location errors of Figs. 2 and 3, respectively, indicates that our method can reduce the influence of the background and has the better location of object center than the kernel-based method for most frames. The average time performance of our method in the ice hockey sequence is about 0.16s per frame, it can reach the requirement of real-time tracking. But when the target becomes bigger like vehicles, the average time per frame gets longer which is about 3s.

• V.    C ONCLUSION

By combining the merits of the region-based method and the contour-based method, we have presented a robust object tracking method. Using the Kalman filter and PPM, we can locate the object effectively in complex condition with partial occlusions, camera motion, clutter, object deformation etc. In order to improve the tracking precision, we used the contourbased method to track the object contour precisely after the target localization. The experimental results demonstrated that our method can achieve a higher tracking precision than that of the kernel-based method, but our method is not competent for real-time tracking when the target is large and fast moving.

In the future, an important direction for us to study is

(a)

(b)

Figure 4. Comparison of the tracking error. (a) Tracking error of Fig. 2. (b) Tracking error of Fig. 3.

15 Frames (a)

(b)

Figure 5. Comparison of the location error. (a) Location error of Fig. 2. (b) Location error of Fig. 3.

that how to combine PPM with other fast algorithms such as mean-shift to improve the time performance and how to remove the shadow entirely. What’s more, we will further study to propose more efficient methods to extract the contour also for saving time.

A CKNOWLEDGMENT

We would like to thank Zhejin Wang for his helpful discussions. We would also like to thank Peidong Zhou for dealing with the problems of typesetting. This work was supported by the National Natural Science Foundation of PRC (No.50908213).