Монобитное быстрое преобразование Фурье радиосигналов на ПЛИС

Аппаратная реализация вычислителя быстрого преобразования Фурье (БПФ), работающего в режиме реального времени, представляет довольно сложную задачу. Основной элементной базой для решения такой задачи в настоящее время являются программируемые логические интегральные схемы (ПЛИС). Наибольшую трудность при реализации алгоритмов БПФ, как правило, вызывают операции умножения. Например, для N -точечного БПФ с прореживанием по времени требуется N ·log 2 N комплексных умножений или 4 N ·log 2 N действительных операций умножения [1]. При достаточно больших N (512 и более) параллельная реализация такого числа умножений затруднительна даже в современных семействах ПЛИС, содержащих встроенные аппаратные умножители [2]. Одним из вариантов решения задачи может быть построение последовательно-параллельных вычислителей БПФ [3]. Однако они имеют довольно сложную структуру, связанную со сложной адресацией памяти промежуточных данных и поворачивающих множителей [4].

Ряд приложений, таких как приемники коммерческой системы глобального позиционирования (GPS) и др., допускает использование аналогоцифровых преобразователей с малым числом разрядов («грубое» квантование сигнала). В этом случае может быть применен способ реализации БПФ, исключающий выполнение операций умножения [5]. Так как для представления поворачивающих

множителей, а также отсчетов входного сигнала используется один бит, такая концепция получила название монобитной. В [5] предлагается полностью параллельная реализация алгоритма моно-битного БПФ, требующая значительных ресурсов ПЛИС. В настоящей статье рассмотрен способ реализации алгоритма монобитного БПФ, позволяющий оптимизировать используемые ресурсы ПЛИС.2

Функциональная схема вычислителя монобитного БПФ на ПЛИС

Наглядное представление о порядке следования входных, выходных, а также промежуточных данных дают сигнальные графы. Разработано большое число вариантов таких графов, отличающихся вариантами перестановок промежуточных результатов и порядком следования отсчетов входных и выходных данных [1]. С точки зрения аппаратной реализации наибольший интерес представляют графы с постоянной структурой. Важной их особенностью является отсутствие необходимости перестановки промежуточных данных при переходе от одного вертикального ряда бабочек к другому. Это позволяет исключить необходимость в дополнительных схемах коммутации данных. Пример сигнального графа 16-точечного БПФ с прореживанием по времени и постоянной структурой представлен на рис. 1, где все вертикальные ряды бабочек имеют одинаковую структуру. Эта особенность, а также отсутствие необходимости в

перестановке промежуточных данных, позволяют реализовать достаточно простую схему конвейерной обработки, показанную на рис. 2.

На первом этапе вычислений входные данные в порядке, соответствующем бит-реверсивной перестановке, загружаются в регистры промежуточных результатов.

Далее входной мультиплексор (MS) переключает входы регистров промежуточных результатов на выходы вычислителя одного уровня (вертикально ряда в сигнальном графе) бабочек. По окончанию цикла вычислений результат сохраняется в регистрах результата. Данные в этом регистре располагаются в нормальном порядке. Как видно из сигнального графа (рис. 1), вычисления на каждом этапе отличаются набором поворачивающих множителей. Для этого в схеме на рис. 2 предусмотрена память, в которой хранятся наборы поворачивающих множителей для каждого из этапов вычисления.

На вычисление БПФ в предлагаемой схеме потребуется log 2 N +1 тактов конвейера, что в большинстве случаев позволяет обеспечить непрерывную обработку в режиме реального времени с частичным перекрытием во времени буферов отсчетов входного сигнала.

Как было показано выше, применение алгоритма монобитного БПФ позволяет полностью исключить операции умножения. Концепция такого алгоритма заключается в следующем.

Алгоритм БПФ представляет собой способ быстрого вычисления дискретного преобразования Фурье:

N - i - j 2 n kn

X ( k ) = ^ ^x ( ⁿ ) e N .

n = 0

Поворачивающие множители W^kn = =exp(– j π kn / N ) представляют отсчеты комплексной экспоненты. В монобитном БПФ поворачивающие множители могут принимать только четыре значе-

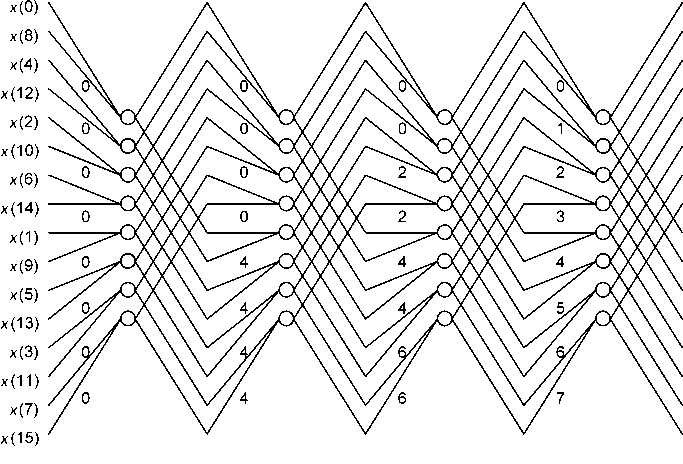
Рис.1. Сигнальный граф

X(0)

X(1)

X(2)

X(3)

X(4)

X(5) X(6)

X(7)

X(8) X(9) X(10) X(11) X(12) X(13) X(14) X(15)

Входные данные

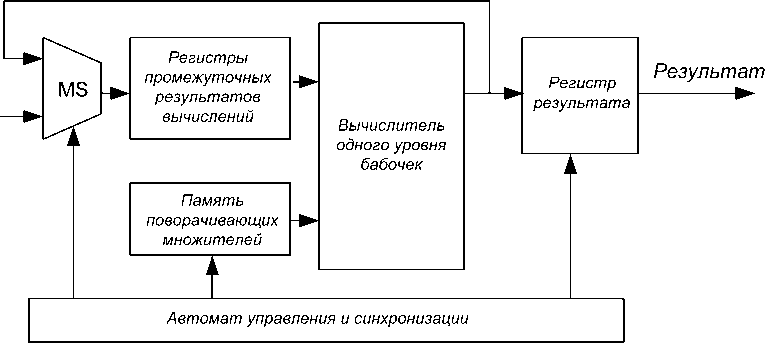
Рис. 2. Схема конвейерного вычислителя БПФ

Монобитное быстрое преобразование Фурье радиосигналов на ПЛИС ния в зависимости от текущего значения аргумента θ = πkn/N:

W^kn = 1 + j , 0 ≤ θ < π/2,

W^kn = –1 + j , π/2 ≤ θ <π,

W^kn = –1 – j , π ≤ θ < 3π/2, W^kn = 1 – j , 3π/2 ≤ θ < 2π.

В силу избыточности поворачивающих множителей при реализации алгоритма используется только пара W^kn = 1 – j и W^kn = –1 – j .

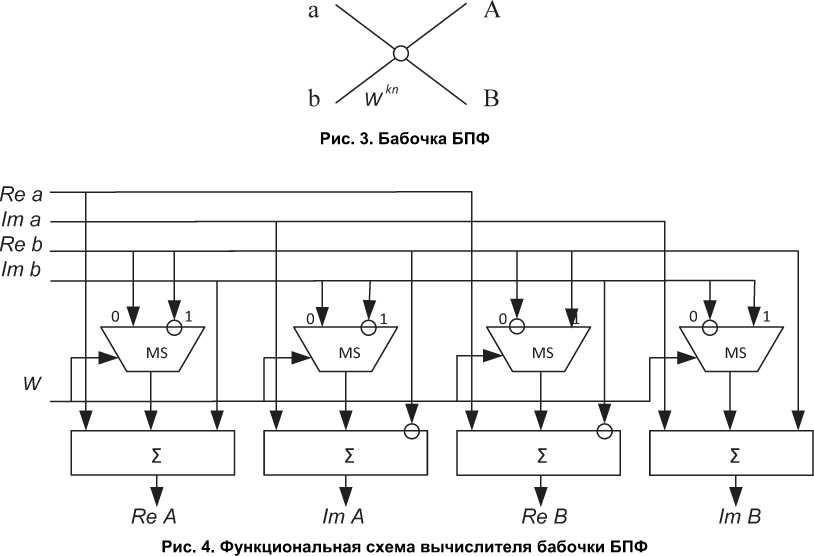
Обозначим входы и выходы бабочки БПФ как показано на рис. 3.

Вычисления в такой бабочке, соответствующей сигнальному графу БПФ с прореживанием по времени проводятся согласно следующим выражениям:

A = a + W^knb , B = a – W^knb .

В приведенных выражениях A , B , a , b , а также W^kn являются комплексными числами.

При реализации бабочки в действительной арифметике для W^kn = 1 – j получаем:

ReA = Rea + Reb + Imb,

ImA = Ima – Reb + Imb, ReB = Rea – Reb – Imb, ImB = Ima + Reb – Imb, а для W^kn = –1 – j соответственно:

ReA = Rea – Reb + Imb,

ImA = Ima – Reb – Imb, ReB = Rea + Reb – Imb, ImB = Ima + Reb + Imb.

С учетом полученных выражений для ReA , ImA , ReB , ImB получаем функциональную схему вычислителя одной бабочки монобитного БПФ (рис. 4). Арифметическая смена знака операндов на схеме условно обозначена символом инверсии.

Выбор поворачивающего множителя осуществляется сигналом W . Состояние W = 0 соответствует выбору W^kn = 1 – j , W = 1 – выбору W^kn = – 1 – j .

Так как для выбора поворачивающего множителя требуется всего один разряд, отпадает необходимость в памяти поворачивающих множителей. На первом этапе вычислений, соответствующем первому ряду бабочек, для всех бабочек W = 0. На последующих этапах, как это следует из сигнального графа (рис. 1) и выражений для W^kn , верхней половине бабочек соответствует W = 0, нижней половине W = 1.

Результаты моделирования в САПР

При помощи САПР Quartus II фирмы Altera была проведена оценка требуемых ресурсов ПЛИС для реализации вычислителя одного уровня бабочек. Для этого была написана программа на языке VHDL, реализующая алгоритм монобитного БПФ, проведена компиляция, анализ временных параметров и затраченных ресурсов. Для исследований была выбрана ПЛИС семейства Stratix III EP3SL150 фирмы Altera [2].

Результаты приведены в таблице. Логические ресурсы выражены в ALUT (Adaptive Look-Up Table) [2] и в процентах от общего числа ресурсов данного типа в ПЛИС.

Заключение

Оптимизация ресурсов ПЛИС, требуемых для реализации алгоритма монобитного БПФ, путем организации конвейерной обработки позволяет сократить число логических элементов в 8–10 раз по сравнению с [5]. При этом скорость обработки

Результаты моделирования

Число точек БПФ Логические ресурсы Максимальная тактовая частота, МГц ALUT % 256 13 700 12,1 134,77 512 30 947 27,2 128,24 1024 49 155 43,3 119,10 остается на прежнем уровне. С учетом того, что результат вычисления БПФ на выходе конвейера формируется менее чем через 100 нс после накопления входного буфера, частота дискретизации входного радиосигнала для БПФ на 1024 точки может составлять порядка 10 ГГц. Это позволяет применять алгоритм монобитного БПФ в современных системах радиомониторинга и радиотехнической разведки.