Morphology of the phase space of one mathematical model of a nerve impulse propagation in the membrane shell

Let Qc R ⁿ be a bounded domain with boundary SQ of class C ” . In the cylinder Q = Qx (0, T ) consider the degenerate FitzHugh–Nagumo system of equations:

„ dv      л , „

£ 1 — = « 1 A v + в 12 w - P 1 1 v , d t

dw     „ n     nз

^ — = a₂ A w + в 2 w - в i v - ^w

2 эt 2        .- with the Dirichlet boundary condition

v(s,t) = 0, w(s,t) = 0, (s,t)e6Q*(0,T).(2)

The sought functions w = w (s,t) and v = v (s,t) describe the dynamics of the membrane potential and the behavior of sodium and potassium currents; вл, Аг,вi,в2,a,a 6R characterize the threshold of excitation, the speed of the threshold of excitation, electrical conductivity and repolarization of the environment. Initially, in [1, 2], a nondegenerate Fitz Hugh–Nagumo system of equations was investigated, where sought functions v and w, simulate the behavior of chemical elements in the membrane. It is characteristic of the system of equations (1) that, with the speed of one of the sought functions in the system, it always significantly exceeds the speed of the other sought function. This phenomenon is called Turing instability [3]. The conditional “regulators” of this behavior of the two initial functions are small parameters s1, s2 at the time derivatives. The system of equations (1) in the case when £1 ^ 0 or s2 ^ 0 using the theory of singular perturbations was investigated in [4, 5]. In this case, the system of equations (1) was considered as a representative of the class of systems of the reaction-diffusion type, which have the form dv        „       . ,     .

^1 — = a1Av + f1(v,w), dt dw

^ 2~ = ^a 2 ^A w + f 2 ⁽ v , w ). d t

This class, in particular, includes problems on the transmission of nerve impulses (except for the already mentioned system (1), the Hodgkin–Huxley system), combustion problems, some models of superconductivity, the Belousov–Zhabotinsky reaction, and others. The study of phase portraits for systems of the reaction-diffusion type was carried out both in the case of systems of a general form [6, 7] and for specific interpretations [8–11]. For some specific systems of reaction-diffusion equations, the existence of an inertial manifold was established [12, 13], and for a system of patterning equations, it was possible to construct a global attractor for Ω = R ⁿ [14]. The phase portrait of the system of equations (1) in the finite-dimensional case, as an example of a system performing relaxation oscillations, was considered in [15], when € 1 >  0. To research the Turing instability in systems of the reaction-diffusion type using the consideration of degenerate equations was proposed by G.A. Sviridyuk and T.A. Bokareva in [16]. The possibility of the existence of several solutions of the Showalter–Sidorov problem v ( s, ⁰ ) = ^v 0

for the degenerate system of equations (1) with condition (2) in the case € ₂ = 0 was investigated in [17]. The presence of the degeneracy of equations in system (1) makes it possible to reduce the system of equations (1) with boundary condition (2) to semilinear equations unresolved with respect to the highest derivative (Sobolev type)

Lx = Mx + N ( x ), ker L * {0}.                               (3)

The statement of the problem of the theory of bifurcation of phase portraits of differential equations in the finite-dimensional case goes back to A.A. Andronov [18]. The word “bifurcation” means “furcation” and is used as the name of any abrupt change that occurs with a smooth change in parameters in any system: dynamic, ecological, etc. cycles, invariant sets and attractors were provided by the works of V.I. Arnold [19]. The first attempts to pass from finite-dimensional systems to the singularity of phase portraits of nonlinear partial differential equations in Banach spaces were undertaken in the works of R.M. Berger, R.M. Church. and I.G. Timouria [20, 21]. They showed that the phase spaces of some elliptic nonlinear partial differential equations have features called V.I. Arnold as Whitney folds or assembly. In the future, in the study of partial differential equations, the definition given by V.I. Arnold modified and acquired the following form. If there exist functions g 0 , g 1 ,..., g_k, belonging to the class C ( B '; R ), such that the equation G(s,v)=0 s equivalent to the equation 0 =g ₀( v ) +g 1 ( v ) s+...+g_k ( v ) s^k+s^k+ 1 , for any v g B ', where B is a Banach space and a function G of class C ” ( B '; R ), then we say that the equation G ( s,v ) = 0 defines Whitney k -assembly over an open set B ' g B .

G.A. Sviridyuk [22] was the first to begin the study of phase spaces for semilinear Sobolev-type equations (3). Later, together with V.O. Kazak [23] proved the simplicity of the phase space for the Hoff equation, when the coefficients of the equations have the same sign, and in work with I.K. Trineeva [24] proved the existence of a singularity such as Whitney folds and folds in the phase space of this equation, but for different signs of the coefficients of the equation. This showed that for semilinear Sobolev-type equations the existence of singularities in the phase space is possible for different parameters of the equation. The essence of the phase space method developed by G.A. Sviridyuk consists in reducing linear and semilinear Sobolev-type equations to an equation x = Sx + F ( x ), defined on a certain subspace, which is understood as a phase space (phase manifold for semilinear equations). This work continues the research begun in [16] for the Fitz Hugh–Nagumo system of equations, generalizing and considering all possible initial conditions and coefficients of the system of equations, including in the case of the parameters at the time derivative of both components of the system are equal to zero.

The article is organized as follows. In the first section, a mathematical model of the propagation of a nerve impulse in the membrane sheath is investigated in the case € 1 =0 and conditions for the simplicity of the phase space of the Fitz Hugh–Nagumo system of equations are found. In the second section, a mathematical model of the propagation of a nerve impulse in the membrane is investigated in the case € ₂ = 0 and conditions are found under which the phase space of a degenerate system has features such as Whitney folds. And also the phase space is constructed in the case € 1 = € 2 =0 . In the third section, examples of constructing phase spaces for each of the studied systems, including those with singularities, are given.

In the cylinder Qx R + consider the system of equations

0 = ^a i ^ v + fi_n w - ⁰ _n v , w_t = a ₂ A w + 0 ₂₂ w —0 ₂₁v

- w

with the boundary condition

v ( s , t ) = 0, w ( s , t ) = 0, ( s , t ) edQx R + .

For simplicity of presentation, we divide the reduction of problem (4), (5) to (3) in three stages.

Stage 1. Take a Banach space    H = H 1 x H₂ = W₂( Q ) x W₂( Q ),   a Hilbert space

X = X1 xX2= L2(Q)xL2(Q), whose scalar product is defined as [x,Z] = , where x = (v,w),Z = (£щ\ <’,’) is the scalar product defined on the space L2(Q). Denote by the space Y dual to H with respect to duality [•<]. For spaces H,X, Y it is true

H c X c Y,(6)

where all embeddings are dense and continuous.

Stage 2. Define linear operators L , M : X ^ Y formulas

[Lx,Z] = , x,Z eX,(7)

[ Mx ,Z] = -a ^-a2 ^< ws. ,ns >, xz e X, dom M = H.(8)

i=1      1      1             i=1       11

By definition, the operators L, M have the properties L e £ (X, Y), M e Cl (X, Y). Note that for all fixed values of the parameters a1,a2 e R \{0} the operator M is L -sectorial [17].

Stage 3. Define nonlinear operator by formula

and put dom N = B = B1 x B2= L4 (Q) x L4 (Q), B * = B* x B* = L 4 (Q) x L 4 (Q) the space dual to B with 33

respect to duality [ • , • ]. For spaces H , X , Y , B , B * at n <  4 it is true

H c B c X c B* c Y,(10)

where all embeddings are dense and continuous.

Lemma 1. [17] For all fixed values of the parameters 0 ₁₂, 0 ₂₂, 0 11 , 0 ₂₁ e R , n <  4, operator

N : B ^ Y belongs to the class C ” .

To construct the space X _a put X _a = X 0 ® X ^ , where X 0 = W 2 ( Q ) x {0}, X a ={0} x X ^a ,

X ^a = L ₄( Q ). For spaces H , X _a , B , X at n <  4 it is true

H c Xa c B с X,(11)

where all embeddings are dense and continuous.

In our case, all solutions of the system of equations (4) lie pointwise in a set P _£ of the form

n

P^ ={xeXa :£ + <в11 vЛ> = <012w,^>}.(12)

i=1           11

Theorem 1. For all fixed values of the parameters a2 e R\{0}, 021,022 eR, a1,вл,012 eR+, n < 4, the phase space P^ of problem (4), (5) is a simple Banach C^ -manifold.

Proof. Let's construct an auxiliary operator

n

< Av, & = £ < 0^ , £ >+<0_n v , ^ > ,                          (13)

i = 1

• v , ^ e H_v Since

The resulting operator A : H ₁ ^ H * is coercive, i.e.

lim    < Av , v > || v HH =

^{|| v ||} H -^+^

lim

^{|| v ||} H ^+^

n

J- ( ^ a ,^ @ 11 v ²

k Q i = 1

( n

\

) ds • J ( X < ^{+ v 2 ) ds}

J k Q i = 1             J

i

—

= +^ .

Moreover, the operator A is strictly monotone, i. e.

n

< ^Av j - AV 2 , v i - ^v 2 >  = J ^{( a} 1 ⁽ X ^v 1 s

Q      i = 1

- v 2 s ) ² + @ 11 ( v i - v 2 ) ² ) ds >0

as soon as v 1 ^ v ₂. Finally, let us show the smoothness of the operator A . Really,

n

| < A v ^ 2 , ^ i > |=| J ( ^ a^ _s. £ 2 s + @ 11 £ 1 £ ₂) ds | < b || Й Ц П2Н H ,

Q i = 1

where the constant b depends only on a ₁, @ ₁₁ and the embedding constants (6). Therefore, the operator A is continuously differentiable, and from this, in an obvious way, its radial continuity follows.

Applying the Vishik–Minty–Browder theorem [25], We obtain the bijectivity of the operator A : H ₁ ^ H * . Construct the operator D ( w) = (A ^-1( w ), w ), dom D = X ^ . Since the operator D satisfies the conditions of the Vishik–Minty–Browder theorem, the statement of the theorem is true.

• 2.    Mathematical Model of the Propagation of a Nerve Impulse in the Membrane Sheath in the

Case of £ ₂ = 0

In the cylinder Qx R ₊ consider the system of equations ' ^v t = ^а 1 Д ^v + @ w ^- P 11 ^v ,

0 = a2 Aw + @22 w - @21 v - w5, with boundary conditions (5). For simplicity of presentation, we divide the reduction of problem (5), (14) to (3) in three stages.

Due to the fact that the right-hand side of equations in system (14), boundary conditions (5) remained unchanged in comparison with (4), (5), stage 1 of the reduction of problem (5), (14) to (3) coincides with step 1 of item 1. The same is true for constructing the operator from step 2. At the same time, the operator will be different from the operator constructed in item 1, since the left side of the equations in system (14) has changed. Therefore, we construct a linear operator L : X ^ Y as follows

[ Lx, Z ] = < v , £ > , x Z g X .                                 (15)

Note, that for all fixed values of the parameters a ₁, a ₂ g R \{0} the operator M is L - sectorial [17].

Stage 3 of the reduction of problem (5), (14) to (3) almost coincides with stage 3 of item 1. The only difference is in the construction of the space. X _a . Take X _a = X 0 Ф X ^ , where

X 0 = {0} x ^( Q ), X ^ = X ^a x {0}. For spaces H , X _a , B , X at n <  4 it is true

H c X _a c B с X ,                          (16)

where all embeddings are dense and continuous. This means that for all fixed values of the parameters @ j g R , i = 1,2, j = 1,2, n <  4, the operator N is a smooth class C ^ ( X _a , Y ).

All solutions of the system of equations (14) lie pointwise in a set P _£ of the form

P

^ 2

= ’ ^{x g X} a ^{: -}< ^v , П > =

/ - @ 22 w + —!— w ³

\  @21      @ 21

n + У \~w w$ , n /  ^X\ @ 21  si   i

.

Lemma 2. [17] Let a1, ви., @12 e R, a2,@21 g R+, @22 g (-»,a2y1), n < 4, where q is the first eigenvalue of the spectral problem

-Аф = иф ,s e Q , ^ ( s ) = 0, s e dQ ,

then for any vector v e X ^a there is a unique vector w e H ₂ such that x = col ( v , w ) e P _£^ .

Lemma 3. [17] For any а ₁, Д р Д₂ e R , а ₂, в ₂₁ e R ₊, в ₂₁ e ( -» , а ₂ ц ), n <  4, phase space of the system of equations (14) is a set P and it is a simple Banach C ” -manifold.

Consider the case вц ⁼ ащ , put

X ^{a 1} = { v ¹e X ^a : < v ¹ , ^ > = 0}, H 1 = { w ¹e H ₁: < w ¹ , ^ > = 0}.

If v e X ^{a 1} and w e H ₂ epresented in the form v = v ¹ + r ^ and w = w ¹ + q ^ , where r , q e R , ^ is the eigenfunction of the spectral problem (18) corresponding to the eigenvalue и , then the set P takes the following form:

Q

- в11 w1 n1 + -ai- ^ w1 n1 + в11         в11Z si s q\

P

^£ i

x e X_n : <

+ ^( w ¹⁺ q ^ ) ³ n ¹ ph

-fi ll r = J ( w ¹⁺ q ^)³ ^ i ds

Q

A

ds ,

)

•

If in the system of equations defining the set (17) is substituted instead of в ₂₁ = а ₂ ц ,, then in order to obtain the first equation of the system (19) instead of n in (17) it is necessary to substitute n = n ¹ , and then to obtain the second equation (19) instead of n in ( 17) must be substituted n = ^ .

Lemma 5. Let а ₂, в ₂₁ e R ₊, в ₂₁ = а ₂Ц, then for any vector v ¹ e X ^{a 1} there exists a unique vector w ¹ e H ¹ such that

Q

, 1.

n ¹ ds = i f" ¥

Q < P ll

11            P ll i = 1

⁺ J ^{( w 1+} q ^ ^{) 3} n ¹ P 11

ds •

Proof. The proof of this lemma is similar to the proof of Lemma 2. Fix q e R and introduce the auxiliary operator A : H p ^ H ₁ ¹

< A ( w ¹+ q ^ ), n > = |f- ^ r¹ Q I ^e ii

022   -L -L &2       -L -L 1

-^J1 w n +—“/ w. n +-- в 11         в 11 ^{Z s}i ^si в11

( w ¹+ q ^ ₁) ³ n ¹ ds ,

,         *1

where H ₁

= { h e H ₂:( h ,^) = 0}. Then

| < A ⁽ w ¹ + q^n ¹><  C i ⁽|| w ¹ || 1 + 1| w ¹ 1|² 1 + 1| w ¹ 1|³ 1 ) || n ¹ II h₂ ^,

^H i         ^H i         ^H i         ¹

where the depend on

constant C i e R ₊ depends on а ₂, в ₂₁, в ₂₁ and the embedding constants (6), but does not w ¹ , П ¹ .

Note that lim    | w1^

^w 1 h ₂1 '■                        ¹

lim

II ■  I H 1

^+»\ Q \

- ^ Ц w ¹ ) ² + ^ £ ( w 1 ) ² + в 11         в 11 ^{Z   s}i

A

1           AW n

— (w 1+ q^i)3 ds • J(X(w1 )2 + (w1 )2ds e11              )   ) ^Q i=1

J

= +» .

Gavrilova O.V.                              Morphology of the Phase Space of one Mathematical Model of a Nerve Impulse Propagation in the Membrane Shell and nn

< A ( w , ■ q ^ ! ) - A ( w ^ + q ^ ), w ¹ - w 2 >  = f /( £ w^ — £ w i ) 2 —

Q4 p21  i =1

- ir( w^ - w’ )2+r(( w^q^i)3 - (w^+q^i)3)( w^ - w^) I ds = P21              P21

nn

^- f /⁽ £ ^w s ■ £ w ^{1 ) 2 -} д ⁽ w ^{1 -} w ^{1 ) 2} +

0 4 e21 i=1        i=1

+ — (wj1 - w£)2((wj' ■q^)2+(wjL+q^)(w^+ q^)+(w^+ q^)2 ds >0, ^21

as soon as w j¹ ^ w ¹ . This means that the operator A : H ^ ^ H 0 ¹ is coercive and strictly monotone.

Moreover,

< < w, wi - f| a Ё^Х"в22 wi+ 3±( w + q^. wi wi ds, w            Qk в21 i-1           P21        P21

where w ^ , w ^ e H ^ , i.e. the operator A is smooth, which means that it is also radially continuous. By virtue of the Vishik–Minty–Browder theorem [25], the assertion of the lemma is true.

Let us turn to the second equation of the system that defines the set (19). Transforming the resulting equation, we get:

q ³II ^ II4 (Q) + 3 q ² f w ¹^ ³ ds + 3 q f ( w ¹ ) ² ^ ² ds + f ^ ( w ¹ )3 ds + P ₂₁ r - 0.           (21)

⁴   00   0

Equation (21) is a cubic equation of general form aq3 + bq2 + cq + d -0 with respect to q. According to Cardano's formulas, any cubic equation of general form can be reduced to the canonical form y3 + py + e - 0 with the coefficients a -II ^ lL (Q),b = 3fw1^3ds,c = 3f (w1 )2^2ds,

Q          Q d - jW w1 )3 ds - P21r,P -

Q

3 ac - b ²      1

2 b ³

------, e - — ----:

9 a ²       2 27 a

bc d

³    3 a ²    a

Res ( q , w ¹ ) - p ³ + e ² ,

R(q, w1) - q21Ы£ (Q) + 2q$w1 ds + f^12(w1 )2ds Q        Q by replacing q - y -— .

3 a

For convenience of further consideration, we introduce the following sets:

H 0 - { w e H ₂ : R ( q , w ¹ )-0},

H + - { w e H ₂ : Res ( q , w ¹ ) > 0}, H ₂ - { w e H ₂ : Res ( q , w ¹ ) < 0}.

Theorem 2. For any a, Pi, P2 e R, a, Pi e R+, r e R, в22- «2Ц, n ^ 4, the phase space of the system of equations (14) is a set Pe2 and it has singularities of the Whitney 2-assembly type.

Proof. The validity of the theorem follows from Cardano's formulas for equation (21) and the definition of Whitney folds.

In the case ^ - s₂ - 0, when the phase space

О^- « 1 А v + P 12 w ^- fin v , 0 - a ₂ A w + P ₂₂ w - P ₂₁ v - w³

and (4) will be a set of the form

P

* 1 =^ 2 = 0

x e Xa

: s

n

X ( « 1 V_{S J} , ? )+ Д^ Л НД₂ w , ? , i = 1

- ^ 22. w

P 21    P 21

w 3 П

a— w. n. P21   si    i

•

• 3.    Examples of Constructing Phase Spaces

Based on the modified Galerkin–Petrov method and the phase space method, an algorithm was constructed that allows one to find the form of the phase space and its image depending on the values of the coefficients of the system and its degeneracy. The algorithm is implemented in the form of a computer program complex for carrying out computational experiments on the construction of phase spaces, including those with peculiarities.

Example 1. It is required to find the form of the phase space of the system of equations

0 = vss - v + w s form q = w1( t)»

w_t = w_ss — w — v — w³ with boundary condition

v ( s , t ) = w ( s , t ) = 0, s e SO , t e (0, T ), at O = (0, n ).

We     represent     approximate     solutions     (25),     (26)     in     the

m v (s, t) = rq\ (s) + v1, w( s, t) = qq\ (s) + w1,     where     r = v1 (t),     v1 = ^vi (t )y\ (s ), i=2

i =2

The phase space (25), (26) is a simple C ^ -manifold. For a given system, the phase space can be described based on:

^{- 2} r + q = ^0, - 5 v ¹+ w ¹ =0.

It is shown in Fig. 1.

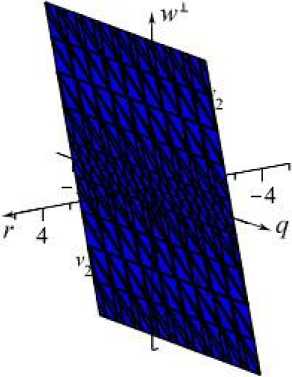
Fig. 1. Phase space of (25), (26)

Example 2. It is required to find the form of the phase space of the system of equations

Vt = v ss - v + w, 0 = w ss - w — v — w³

with boundary condition

v ( s , t ) = w ( s , t ) = 0, s g dQ , t g (0, T ),                                (29)

at Q = (0, n ).

We     represent     approximate     solutions     (28),     (29)     in     the     form

m v (s, t ) = r^( s) + v1, w( s, t ) = qq>1( s) + w1,     where r = v1( t),     v1 = ^v. (t )щ (s ),     q = w1(t), i=2

i=2

According to Theorem 2, in the case when s ₂ = 0, the phase space (28), (29), under certain conditions, can contain a Whitney 2-assembly. For a given system, the phase space can be described on the basis of:

• -3q3 - 6q(w1 )2 + 2nr + 4nq_

  --;= 0,

<                  2n(30)

• -6 q 2 w1 - 3( w1 )3 + 2nv1 + 10nw1 _ 0.

I

Phase space in the case when £ ₂ = 0 shown in Fig. 2.

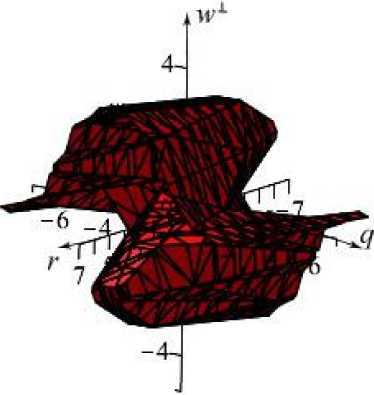
Fig. 2. Phase space of (28), (29)

Example 3. It is required to find the form of the phase space of the system of equations /  ⁰ = v ss ^{- v +} w ,

0 = w s _s - w—v - w³

with boundary condition

v(s, t) = w(s, t) = 0,s g dQ, t g (0, T), at Q = (0,n).

We     represent     approximate     solutions     (31),     (32)     in     the     form v (s, t ) = r^l( s) + v1, w( s, t ) = qq\( s) + w1,    where r = v1( t),     v1 = ^( t^ (s),     q = w1( t),

=2

w ¹ = &⁽ t ) ^ ⁽ s )• i=2

According to Theorem 3, the phase space (31), (32) in the case when s 1 and s ₂ both are zero, is the intersection of the phase spaces (27) and (30), it is shown in Fig. 3.

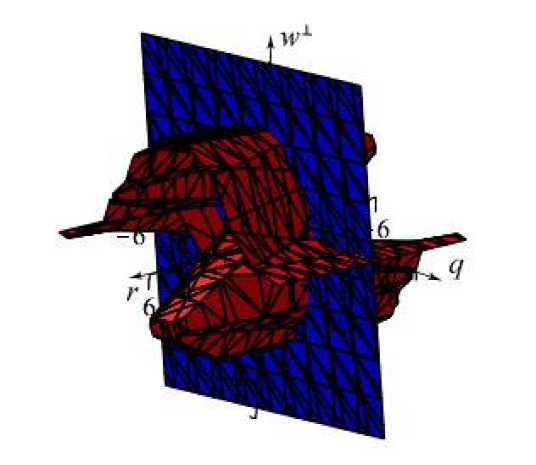
Fig. 3. Phase space of (31), (32)

The research was funded by RFBR and Chelyabinsk Region, project number 20-41-740023.

Received July 12, 2021

Bulletin of the South Ural State University Series “Mathematics. Mechanics. Physics” 2021, vol. 13, no. 3, pp. 14–25