Multi-Level Access Priority Channel Allocation with Time Threshold in Global System for Mobile Communications (GSM) Networks

Published Online October 2015 in MECS

• I.    Introduction

  Cellular telephone systems in the early 1980s were analog thereby faced with the inability to handle the growing capacity needs in a cost-efficient manner. This problem occurs because the analog transceiver can only handle one call at a time. Digital technology was introduced to overcome the problems of analog [1]. The introduction of digital systems gave rise to second generation of cellular telephone, at this point; Global System for Mobile Communications (GSM) was released. GSM is more advanced than analog systems and handles more subscribers than the analog telephones [2]. It offers

high quality voice communication and low bandwidth data connections for fax and short message service (SMS) at the inception. The success of voice communication in GSM brought about the introduction of data connection services like browsing, videos, multimedia, and e-mail. The demands of GSM services have increased tremendously thereby necessitating the need for a reliable and always available infrastructure to support these [3][4][5]. All these outlined features have led to congestion on the GSM Network. Unfortunately, today’s infrastructure have failed to address this issue effectively. Even the specifications issued by the telecom standardization bodies did not even address this issue of exaggerated call requests that have led to the problem on the GSM Network [6].

The means of allocating the scarce channels is another issue on the overall performance of the GSM networks.

Several papers have been presented on this issue and three principal categories have been identified and they are; fixed

Channels allocation (FCA), dynamic channel allocation (DCA) and hybrid Channel Allocation (HCA) [7], [8], [9]. In FCA, a set of channels is permanently allocated to each cell based on pre-estimated traffic intensity. When a user requests for a channel, it searches the free channel in its own cell, if there is free channel, the communication is granted, otherwise, is blocked. DCA allows dynamic allocation of channels as new calls arrive in the system. The entire sets of free channels are kept in a central pool and they are accessible to all the cells. As soon as a call finishes using a channel, it will automatically return to a central pool where it can be accessible to all the cells in the base station. In HCA, some channels are allocated permanently to each cell and the remaining ones are on call by call basis. In other words, HCA is an integration of FCA and DCA schemes.

In each of the channel allocation schemes, varying method have been proposed and investigated, more are still going to be proposed and investigated because of the escalating number of users always being experienced on the GSM and related networks. Due to the high demand of data on GSM networks, the channel allocation strategies are affected. New channel allocation strategies that will accommodate the data and voice traffics on GSM network have to be implemented. Since the Radio Resource Manager (RRM) is the part of GSM Network that is in-charge of optimizing the usage of radio resources, new channel allocation strategies were evolved based on resource sharing algorithm implemented at RRM [10].

• II.    Handoff

Cellular systems deploy smaller cells in order to achieve high system capacity due to the limited spectrum. Due to this scarcity, the frequency band is divided into smaller bands and those bands are reused in non interfering cells [11]. When a subscriber with an active call crosses cells, the call should be transferred from one cell to another in order to achieve call continuation during this cell boundary crossing. Handoff is the process of changing the channel of the current connection while communication is in progress [12][13]. It is always occur when a call is crossing a cell boundary or there is deterioration in signal quality in the current channel. In the process of handoff, if a target cell has some unoccupied channels, then, it assigns one of them to the handoff call, otherwise, is either the call is dropped or delayed it for a while. The reason why handoffs are critical in cellular communication systems is that neighboring cells are always using a disjoint subset of frequency bands, so negotiations must take place between the mobile station (MS), the current serving base station (BS), and the next potential BS [14][15] .

Handoff is of two types - hard and soft handoffs. The hard handoff occurs when the communication channel is released first and the new channel is acquired later from the neighboring cell whereas a soft handoff can establish multiple connections with neighboring cells [16]. In hard handoffs, current resources are released before new resources are used while in soft handoffs, both existing and new resources are used during the handoff process. Hard handoff is used in Frequency Division Multiple Access (FDMA) and Time Division Multiple Access (TDMA) while soft handoff is used in Code Division Multiple Access (CDMA)[16][17]. GSM uses the Combination of FDMA and TDMA, so in this paper, anytime handoff is mentioned, it is assumed to be hard handoff.

• III.    Retrial Queue

Queues with repeated attempts have been widely used to model many real situations in telephone registration systems, web access, call centres, telecommunication networks and computer systems [18]. Queueing network models are also employed in the traffic modeling of cellular mobile systems, such as GSM, General Packet Radio Service (GPRS) and other higher generation of cellular systems. Most of the studies did not consider queueing systems with retrials but the work of Tran-Gia and Mandjes demonstrated that the retrial phenomenon is not negligible in the context of cellular systems because of the significant negative influence on the system performance measures [19],[20],[12]. The main characteristic of retrial queues is that if an arriving customer finds all servers busy and call not wait in queue, he leaves the service area, but after some random or predetermined time repeats his demand [20],[21].

• IV.    Related Works

Leong et al [22] examine the problem of resource allocation and call admission control (CAC) in the cellular networks, they analyzed priority based resource sharing scheme for voice and data services. The voice service has a high priority over the data service in thier model. In the proposed model, data service will only use the left over capacity after servicing the high priority voice. Also, the load adaptation and bandwidth adjustment policy were proposed for adaptive CAC. This work regarded only two traffic classes, voice and data traffic. Also, in the model, the data traffic might be starved especially when there is a heavy presence of voice users.

Budura et al [9] examine the problem raised by the presence of voice and data traffic in a system. They proposed three strategies based on partial partitioning allocation scheme. In this case, some channels are reserved for the permanent use of individual traffic and some are to be shared by all the traffic types. The strategies are full-rate, half rate voice traffic technique and dynamic allocation technique. They considered two traffic types namely the voice and data. They estimated the blocking probabilities for each of the strategies used in their paper.

A cellular network was studied under dynamic channel allocation (DCA) since DCA is very flexible in using any of the available channels in any cell as long as the interference level is below a given threshold [10]. In their study, they propose a two-dimensional Markov Chain model to analyze the performance of the system in terms of blocking probabilities. They consider a cellular network along the corridor of an office or along a busy road called the linear Highway System, then, they compute the blocking probabilities in that system.

An analytical model of a time-threshold based bandwidth allocation scheme for voice calls in cellular networks was developed by Candan and Salamah [23]. Time-threshold based bandwidth allocation scheme (TTS) was modeled using a two-dimensional Markov chain and numerical analysis was presented to estimate blocking probabilities of new calls, dropping probabilities of handoff calls and system utilization. The main idea in this scheme is based on monitoring the elapsed real time of handoff calls and according to a time-threshold parameter; a handoff call is either prioritized or treated as a new call. It is worthy to mention that TTS can be implemented easily since it uses the elapsed real time of a call which is already recorded in all systems for billing and other purposes.

A generalization of the homogeneous multi-server finite source retrial queue with search for customers in the orbit was studied [24]. The paper introduces balking and impatience customer’s requests who arrive at the service facility with a limited capacity and FIFO queue. Arriving customers may balk, that is, they either join the queue or go to the orbit. In this study, a finite-source retrial queues with multiple homogeneous servers that conduct orbital search was investigated. The influence of customer balking and impatience as well as the effect of the service area’s finite capacity on the mean response time was also discussed. Customer balking refers to discouraged customers that are entering the orbit although there are some spaces available in the waiting queue. Joining the orbit might be more attractive than joining a long queue. Impatience lets queueing customers leave the queue and join the orbit instead. For instance, customers that joined the queue might be able to observe the waiting queue while waiting. This allows them to estimate the mean service time, queue length and their remaining waiting time. Based on this estimation, they may decide to leave the queue and retry to get service later. The performance measures of this model were obtained by numerical analysis carried out using the MOSEL-2 performance evaluation tool.

A study was conducted on the retrial attempts on the performance analysis of finite-source retrial queues with heterogeneous sources operating in random environments, where the system parameters are subject to randomly occurring fluctuations [20]. All random variables involved in the model construction were assumed to be exponentially distributed with a parameter depending on the source index and on the state of the corresponding random environment. The aim of the study is to give more realistic models for finite-source retrial queues since the different request for arrival, service and retrial rates are subject to random fluctuations. The result shows that retrial phenomenon increases the handoff call arrival rate, the fresh call blocking probability, and the grade of service.

• V.    Model Description

A cellular network model of one cell only is considered in this work. It is assumed that we are treating homogenous cells, that is, cells that are identical and have the same traffic parameters, so it is enough to investigate one cell, and the handoff effect from the adjacent cells to this cell and from this cell to adjacent cells is described by handoff processes [22]. The total C channels in the cell are dynamically assigned to three pools using Partial Partitioning schemes as shown diagrammatically in Fig 1.

q 1

q 2

q 3

Fig.1. Complete sharing schemes

Pool 1 has q 1 channels for voice traffic exclusively,

Pool 2 has q2 channels shared for special voice class, handoff voice and handoff data,

Pool 3 has q₃ channels for data traffic exclusively,

Thus

Note that q 1 , q 2 and q 3 are not specific channels but just a label for the pools of channels. The reason for this model is to guarantee a level of quality of service (QoS) for voice and data traffic since the practice is that voice calls always have priority over data users; therefore, a specific sum of channels should be exclusively reserved for data users. As a result, real time services like videos, browsing can be given a level of satisfaction [23][24]. Furthermore, each of the pools will be shared by different classes of services using a complete sharing, that is, each pool will be allowed to be accessed by different classes of call available in the pool.

The following assumptions are made:

• i.    The number of channels in the cell is C

• ii.    The C channels are divided into three parts namely, q_1, q_{2, and} q3, though, the size of each part is not fixed and can be decided by the operator but later re-adjusted based on the results of performance monitoring that would be carried out by the operator.

• iii.    The number of special voice users = s v

• iv.    The number of handoff voice users = h v v. The number of redialing voice users = r v vi. The number of new voice users = n v

• vii. The number of data users = d

• VI.    Voice Traffic Model

When a new voice call arrives, it enters q₁ if there is a free channel available. Otherwise, it is blocked. When a handoff voice call arrives, it first enters q₂ if there is a free channel there, else it enters q 1 if there is a free channel, or else, it preempts handoff data call if all channels in pool 2 are occupied and there is at least one handoff data call there, otherwise, is blocked. Handoff voice calls is given a preemptive priority over handoff data calls because data can usually tolerate some degree of service degradations while voice is more delay sensitive [14]. When a new voice call is blocked, it is assumed that it goes into orbit and a retrial call has to be made [19]. Also, there are some high power mobile stations that have the feature of automatic redial, this shows that the subscriber does not need to do the retrial call personally but the MS will automatically do it. Cellular systems with customer redials and automatic redial have been treated in literature [16][25].

A retrial call queue is possible in cellular systems since the setup of a call is done on a separate control channel, which can provide the system with a way of queuing calls that did not cease any communication channel without affecting the transmission channels [26]. As a result of this retrial calls, the QoS will be impacted.

The retrial call is given a priority over a fresh call but with a time threshold. If this threshold expires and the retrial has not been able to cease any channel, then, the call will automatically become a fresh call. The retrial that happens with the voice handoff is not considered here because as long as the signal strength of the MS to the BS or MSC has not being totally cutoff, the handoff voice call will still be connected and at the same time, the handoff voice call will be queued in the handoff buffer until it seizes the free channel or forcefully terminated when the handoff threshold time expires. It is assumed that a terminated subscriber might not call back since it has been connected for some period of time but if there is need for the subscriber to call back, the call will now be a fresh call and follow the requirements that govern a fresh call.

• VII.    The Time-Threshold Scheme (TTS)

Guard channel scheme (GCS) gives priority to handoff calls for both data and voice, by reserving some channels for the handoff calls. GCS achieves low dropping probability, compared to blocking probability of new calls but at the cost of degradation in channel utilization. However, according to the complete sharing scheme (CSS) all available channels in a cell are shared by handoff and new calls. Therefore, CSS scheme minimizes the new call blocking probability and maximizes channel utilization. However, it is difficult to guarantee the required dropping probability of handoff calls [27]. Generally, GCS scheme is preferred by users since it decreases dropping probability (P d ), and CSS scheme is preferred by service providers since it maximizes system utilization.

In this work, a new voice call is served if the amount of occupied bandwidth is less than q₁ upon its arrival. However, a prioritized handoff voice call is served as long as there are free bandwidth units in either q 1 or q 2 bandwidth upon arrival or at least one n v is present. According to TTS, handoff calls that have elapsed real time less than time-threshold t e are prioritized [23]. That is, such handoff calls are accepted as long as the amount of occupied bandwidth in the cell is less than the total capacity, C. On the other hand, handoff calls that have elapsed real time less than time-threshold t_e but blocked as a result of lack of free channels will be queued and allowed to seize a free channel on the principled of first-come first-served (FCFS) before the expiration of t_e. If the handoff was unable to seize any free channel before the t e expired, then it will be dropped forcefully. The time-threshold parameter (t e ) is a value which is less than the mean call duration and can be adjusted by the service provider. The value of t e affects the prioritization of handoff calls. That is, as t e increases, the number of prioritized calls increases. Therefore, te will serve as a threshold for classifying handoff into either prioritized call or new call. The service provider is still at liberty here to adjust the time-threshold parameter (t e ) value which must be less than the mean call duration and can still be adjusted

• VIII.    Traffic Performance Analysis

In this section, the system performance is analyzed by considering a homogeneous mobile network, where all cells have the same property. In each cell, the arrivals of voice (new, retrial, handoff and special call) and data are Poisson distributed with rate λ vn , λ v r , λ vh , λ vs , and λ d respectively. Thus, the total arrival rate for voice traffic is

^ v = ^ vn + ^ vr + ^ vh + ^ vs      (2)

while that of data traffic is ^ , respectively. The service times of voice (new, retrial handoff and special call) and data (new and handoff call) calls are assumed to follow a negative exponential distribution with means, ¹ ^ nv ,1 M rv , 1 M hv ,1 M sv and 1 M d respectively.

The total average service time of a voice call is defined as

M v

— + — + — + —

M nv ^M rv ^M hv    M sv

As explained in the earlier section, a handoff voice and retrial calls are controlled according to their threshold time (te). Recall that, both handoff voice and retrial calls are accepted as long as the amount of occupied bandwidth is less than the bandwidth threshold q1 and the te is less than the elapsed time. However, when the amount of occupied bandwidth is greater than or equal to q1 and less than q2 bandwidth units, only handoff voice calls are accepted but still subject to the fact that the te of handoff voice call has not expired. Since te affects the prioritization of handoff calls That is, as te increases, the number of prioritized calls decreases, β implicitly affects the arrival rate of prioritized handoff calls. Then, the arrival rate of prioritized handoff calls Ahv is directly proportional to both β and the arrival rate of handoff calls, λvh.

Therefore, ^ hv can be written as

A v = в A v            (4)

Let β be defined as the percentage of the prioritized handoff with the following heuristic formula [23], в _ 1 Mhv

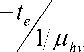
while the arrival rate of retrial call,

^rv = в .^rv

where в = 1 ^rv

—

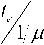
rv

The normalized offered load of the system (q) for voice measured in Erlang, is defined to be i я я л я nv      rv      hv      sv

C ^— q 3 L M nv   M rv   M hv   M sv

The voice call intensity is defined as the ratio of call arrival rate to call service rate. That is, voice call intensity г =

я я я, я nv      rv      hv      sv

M nv    M rv    M hv    M sv

These assumptions have been found to be reasonable as long as the numbers of mobiles are much more than the number of channels [26].

• IX.    The Underlying Markov Chain of Voice Traffic Model

The proposed scheme in this work can be modeled with a 5-D Markov chain as shown in Fig. 2.

The state space of the Markov chain is

P ( i : j : k : l : m ) = lim P ( q + q ₂)( t ) = i , ( q + q ₂)( t ) t ^to

= j, q i ⁽ t ) = ^k, q i ⁽ t ) = l, ⁽ q 2 ⁺ q з ⁾⁽ t ) = m )

Let S be the set of feasible states, s = {(i, j,k,l,m) | 0 < i < qi + q2,0 < j < qi + q2,

0 < k < qx ,0 < l < qx ,0 < m < q2 + q3} where i is the number of Special call, j is the number of Handoff, k is the retrial call, l is the number of new call, m is the number of data call For all i, j, k, l, m G s, the transition rates of the Markov process are described as follows:

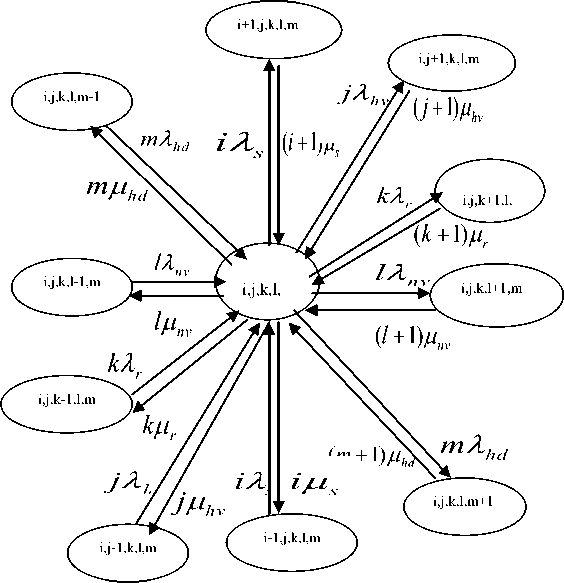
Fig.2. A five state Markov chain

(a) S_v( i , j , k, l, m ) is the transition rate from state ( i , j , k, l, m ) to ( i+ 1, j , k, l, m ). A special voice user is admitted into the system as long as the number of Sv users in the system is less than the number of available channels in q 1 and q 2 . Therefore, S v ( i , j , k, l, m ) can be written as

S_v( i , j , k, l, m ) is the transition rate from state ( i , j , k, l, m ) to ( i- 1, j , k, l, m ).

S v i , j , k , l , m

i M sv

0,

if     0 < i <  q i + q 2

otherwise

S _v i , j , k , l , m

^ sv ,

. 0,

if     0< i <  q i + q - 2

otherwise

(b) Hv(i, j, k, l, m) is the transition rate from state (i, j, k, l, m) to (i, j+1, k, l, m). A handoff voice user is admitted into the system when the total number of Sv and Hv is less than the number of available

channels in q1 and q2. Therefore, Sv(i, j, k, l, m) can be written as

E, i, j,k,l,m

v i , j , k , l , m

A hv ,

^

0,

if    i + J <  q i + q 2

otherwise

H v ( i , j , k, l, m ) is the transition rate from state ( i , j , k, l, m ) to ( i , j-1 , k, l, m ).

j H hvv

H v i, j , k , l , m — <

if ⁱ + j <  q i + q 2

otherwise

(c) Rv(i, j, k, l, m) is the transition rate from state (i, j, k, l, m) to (i, j, k+1, l, m). A retrial voice user is admitted into the system when the total number of Sv, Hv and Rv are less than the number of available channels in q1. Therefore, Sv(i, j, k, l, m) can be written as

R _v i, j,k,l,m

if    i+j+k < qi otherwise

R v (i, j, k, l, m) is the transition rate from state (i, j, k, l, m) to (i, j, k-1, l, m).

k ^ rv

R v i,j, k , l , m — ‘

if   i + j + k <  q 1

otherwise

(d) Nv(i, j, k, l, m) is the transition rate from state (i, j, k, l, m) to (i, j, k, l+1, m). A new voice user is admitted into the system when the total number of Sv, Hv, Rv and Nv are less than the number of available channels in q1. Therefore, Nv(i, j, k, l, m) can be written as

N _v i, j, k, l, m

A nv ,

if

i + j + k + m <  q 1

0,

otherwise

N v (i, j, k, l, m) is the transition rate from state (i, j, k, l, m) to (i, j, k, l-1, m).

	l » nv ,	if	i + j + k + m <  q 1
N v i,J,k , l , m — ^
	. 0,		otherwise

The balance equation for the Markov process is

expressed as

i A s (i, j, k, l, m) + i » (i, j, k, l, m) +j A (i, j, k, l, m)

+ j > hv (i, j, k, l, m) + k A , (i, j, k, l, m) + k » , (i, j, k, l, m)

+ lAnv(i,j,k,l,m) + l» nv( i,j,k,l,m)

. + m A hd (i, j, k, l, m) + m A hd (i, j, k, l, m)

П - 1, J , k , l , m ^{i A} s ^{( i - 1, j} , k , ^l , m ) ^{+ n} i + 1, j , k , l , m . ^{( i +} 1) » s ^{( i +} 1, ^j , k , ^l , ^m )

^{+ n} i , J - 1, k , l , mJ^A hv ^{( i} , ^{j -} 1, k , ^l , m ) ⁺ⁿ i , J + 1, k , l , m . ^{( j +} 1) » h ^{( i} , ^{j +} 1, k , ^l , m )

^{+ n} i , j , k - 1,l , m ^{k A} r ^{( i} , ^j , ^k - 1, ^l , m ) ⁺ⁿ i , j , k + 1,l , m . ^{( k +} 1) » r ^{( i} , ^j , ^{k +} 1, ^l , m )

^{+ n} i , J , k , l - 1, m . ^{l A} nv ^{( i} , ^j , ^k , ^{l -} 1, m ) ^{+ n} i , j , k , l + 1, m . ^{( l +} 1) M „v ^{( i} , ^j , ^k , ^{l +} 1, m )

By applying the constraint

2 ^П , , j , k , l , m ^{— 1} to the set of

balance equations, the steady-state Probability p are obtained to evaluate the performance metrics of the system.

The steady state probabilities is calculated directly from the above equations using multi-dimensional principle [29]

^ i , j , k , l , m

1    fliv    fk fk ^L1

where P(0, 0) is the steady-state probability of the system being idle.

From    the    normalization    equation    (i.e.

2 _s P, , j , k , l , m , n ^— 1 ) we obtain ^{P(0, 0)} as

C - q з((!  A.C A.C         a-P V

P (0,0,0,0) — 2 ( - sv----hv---------nv---^d—    (20)

a — 0                 a !

where A = i + j + k + l +m .

Hence the state probability is given as

f,j       ll F1 /С-qз nit,„— 1аа-'^аГ^аП^а1- /?(-„ + -,, + -„ + -„, + -,)a/«!    (21)

ⁱ , ^j,k,^l,m [ i ! j ! k ! l ! m ! J/ _a^ ” hv rv " ^d '

Using the state probability, the following performance metrics are derived thus:

i. A special voice (sv) call will be blocked when the number of sv calls in the system equals to C-q 3 upon arrival. Thus, the blocking probability of sv calls, Psb , is expressed as

c ^- q з

P =y^.

bsv               i, j,k,l,m i—0

ii. A handoff voice (hv) call will be blocked when the total number of sv and hv calls are equal to C-q3 upon arrival. Thus, the blocking probability of hv calls, Phvb, is expressed as

c — q 3 c — q 3 — i

P bhv = 2 2^ , , _t , i , m

i =0 j =0

• iii.    A retrial voice (rv) call will be blocked when the total number of sv, hv and rv calls are equal to q1 upon arrival. Thus, the blocking probability of rv calls, Prvb, is expressed as

c - q . 3 C - q з - i q i ^{— (} i + ^j )

^P brv = 2 2  2 ^{П (} i , ^j , ^k , ^l , m )

i = 0 j = 0     k = 0

• iv.    A new voice (nv) call will be blocked when the number of when the total number of sv, hv, rv and nv calls are equal to q1 upon arrival. Thus, the blocking probability of nv calls, Pnvb, is expressed as

C - q з C - q з - ⁱ q i - ^{( i} + ^j ) q i - ^{( i} + ^j + ^k )

P bn = 2 2  2   2 n (i, j , k , i , m )

i = 0   j = 0      k = 0        l = 0

• v.    A handoff data call (hd) call will be blocked when the number of when the total number of sv and hv, calls are equal to q2 upon arrival and number of calls of hd are equal to q3. Thus, the blocking probability of hd call is expressed as

C - q з C ^— q з ^— iq 2 ^{— (} > + i )

P bhd = 2 2  2 n (i, J , k , l , m )      (26)

i = 0 j = 0      k = 0

• X.    Analytical Simulation and Performance Results of Voice Communication Model

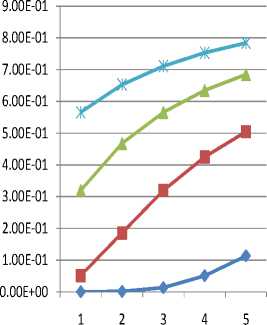
In this work, the parameters used in the analytical simulation are listed in the Table 1. A situation where all call types are accessing the network within a range of an hour is presented in Fig 3. The impact of blocking of the new call is equivalent to the impact of the traditional blocking of Erlang B since all call types except new call can preempt new call traffic.

As shown in the graph, new voice call blocking shows the same probability with traditional Erlang B since all the types of calls are assumed to be present. In traditional Erlang B, there is no differentiation of call type, all calls were assumed to be of single type [30], [31]. Pbsv is the least since this is the call type that cannot be blocked by any other user at any point in time. Pbhv follows the Sv in the other of blocking probabilities while Pbrv followed Pbhv since hv is having lower priority compared with the Sv but has higher priority than rv. Rv has a lower priority than hv but higher priority than nv. In erlang B, calls dropped or blocked are assumed to be lost completely, there is no opportunity of call queueing; therefore, this also contributed to the probabilities characteristics [30].

Table 1. Analytical Simulation Parameters

Total channel in the cell	22
Total channel for pool q1	11
Total channel for q2	6
Total channel for q3	5
Service rate 1/ ^	180s, 120s
Arrival rate for voice special λ s	1.67 – 5.0 call/s ≈ 100 – 250 calls
Arrival rate for voice handoff λ h	2.5 – 5.83 call/s ≈ 150-250 calls
Arrival rate for voice retrial λ r	3.33 – 6.67 call/s ≈ 200-300 calls
Arrival rate for voice new λ n	5 – 8.33 call/s ≈ 300 – 500 calls
Arrival rate for handoff data λ hd	2.5 – 5.83 call/s ≈ 150-250 calls
Offerred load in erlangs for special ρ s	5.0 – 15, 3.3 - 10
Offerred load in erlangs for special ρ h	7.5 - 17.5, 5 – 11.7
Offerred load in erlangs for special ρ r	10 – 20, 6.7 – 13.3
Offerred load in erlangs for special ρ n	15 – 25, 2.5 – 9.2
Offerred load in erlangs for special ρ h	7.5 - 17.5, 5 – 11.7
P bsv	Blocking Probability of special voice call
P bhv	Dropping Probability of handoff voice call
P brv	Blocking Probability of retrial voice call
P bn	Blocking Probability of new voice call
P bhd	Dropping Probability of handoff data call

Pbsv (180s)

Pbhv (180s)

Pbrv (180s)

Pbn(180s)

Pb with trad. erlang B

Fig.3. Full accessibility

The voice blocking and dropping probabilities of Sr, rv, nr and hv with the threshold is shown Fig 4. So instead of allowing the real elapsed time to be used, te is used instead. The probabilities obtained under te is compared with the one without te. It shows that the blocking and dropping probabilities are lower for all call types.

Fig.4. Graph for the Full accessibility with te

The simulation done under the 120s service rate for all users with appropriate priorities is shown in Fig 5. It shows that both the dropping and blocking probabilities of all the call types are reduced compared with the simulation done under 180s. The only side effect is that people that wanted to have extension beyond 120s may be dropped if there is no free channel available. The effect of te on handoff under 120s service time is shown in Fig 6. Since handoff is having priority over retrial and new, applying te will further make more channels available for both the new and retrial and at the same time, the handoff will not be much affected since they would have communicated to some appreciable level.

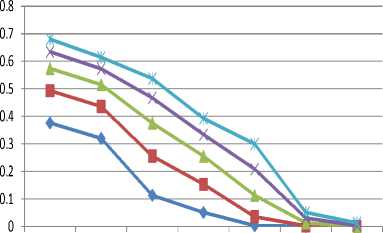
Fig. 7 shows a situation where only hv are present in the system and no Sv priority call. It shows a great reduction of probabilities when still compared with the traditional erlang B where there is no differentiation. Fig. 8 shows a further reduction when done under te threshold in this situation.

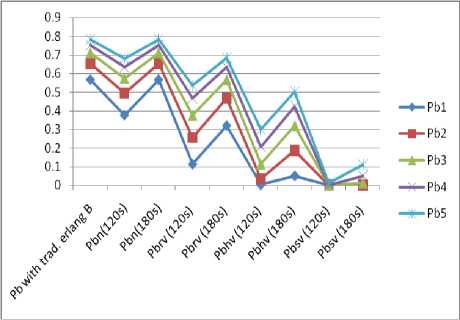
Fig.5. Graph for full accessibility with two service rate

- ♦ -PB1

-•-PB2

-* ■ PB3

PB4

-*-PB5

Pbn(120s) Pbn(120s)   Pbrv      Pbrv     Pbhv     Pbhv     Pbsv with te    (120s)     (120s)    (120s)     (120s)    (120s)

with te               with te

Fig.6. Full accessibility with 120s service rate and te

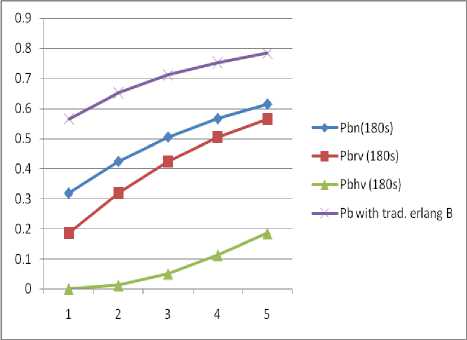
Fig.7. Full Accessibility of Call types with Hv Presence Only

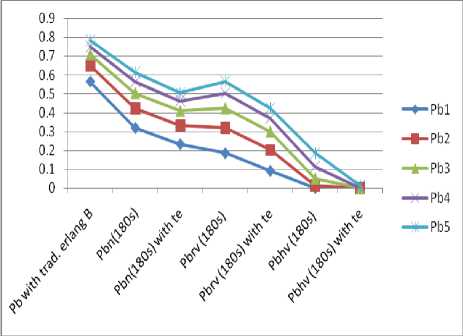
Fig.8. Full Accessibility of Call types with Hv te

Fig. 9 shows comparisons of probabilities of blocking and dropping in simulation done using 180s and 120s for service time when only hv are present in the system and no Sv priority call. The results show a great reduction of probabilities when compared with the traditional erlang B where there is no differentiation.

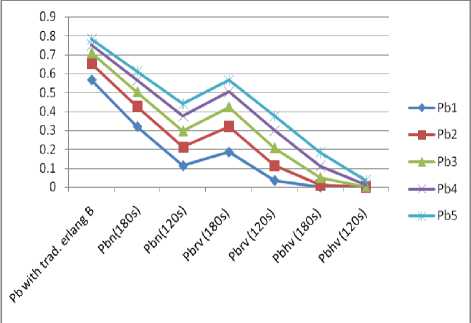
Fig.9. Graph for Full Accessibility of Calls type with Hv Presence Only of 180s and 120s service rate

Fig. 10 shows a lower reduction when done under 120s service rate and a further reduction when done under te threshold.

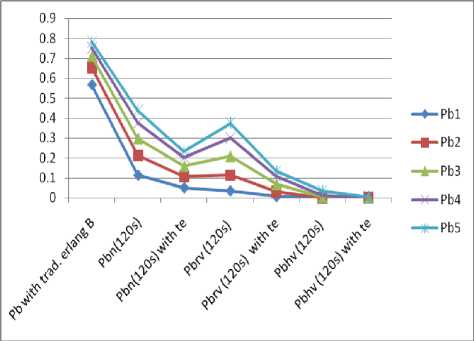
Fig.10. Graph for Full Accessibility of Call types with Hv Presence Only under 120s service rate and handoff t e

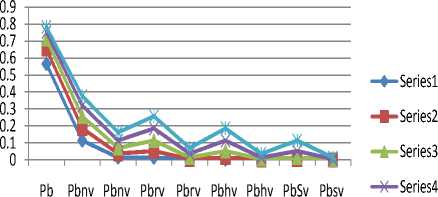
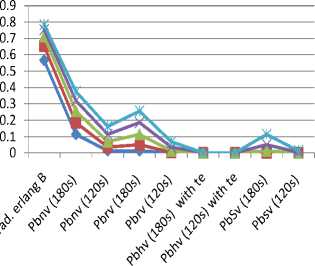
The accessibility of each call type without the presence of any other priority calls that shows in this situation, the new user will have access to cell only is given in Fig. 11. This happens mostly in cities and town where user movement during the call time is reduced and only user is assumed to be stationery during the call period. Fig. 12 shows a further reduction in handoff probabilities when te is applied to both the 180s service rate and 120s service rate respectively

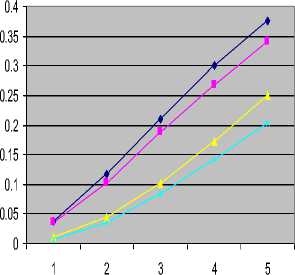
Fig. 13 shows the accessibility of data call type with the presence of voice call that has priority over the data calls. This shows that the data call will always have higher blocking probability in as much as there is a voice call in the system. Therefore, when a threshold (t e ) was applied to the voice call, thus, prevent the voice call to occuppy the channel without a check. This situation reduced the data call blocking as shown in Fig.14.

with (180s) (120s) (180s) (120s) (180s) (120s) (180s) (120s)    -*-Series5

trad.

erlang B

Fig.11. Graph Full Accessibility of each Call types of 120s and 180s service rate

-ф-Series1

- ■ -Series2

-*-Series3

Series4

-ж-Series5

Fig.12. Full accessibility of each call types of 120 and 180s service rate with te

-+- Pbhd in the presence of voice without te using 600s service time

-•— Pbhd in the presence of voice with te

Pbhd in the presence of voice without te using 300s service time

Pbhd in the presence of voice with te

Fig.13. Voice call type impact over handoff data call with te

Blocking probabilities of Data traffic for all data types in the presence of voice call when simulation was done with service time of 600s and 300s is shown graphically in Fig. 15. The blocking probability under 600s was higher than the one done with 300s.

-+- Pbhd in the presence of voice without te using 600s service time

-I- Pbhd with te in the absence of voice for 600s service time

Pbhd in the presence of voice without te using 300s service time

Pbhd with te in the absence of voice for 300s service time

Fig.14. Voice call type impact of over handoff data call with t e

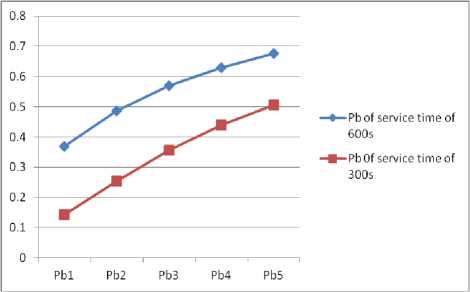
Fig.15. Graphical representation of Data traffic probabilities in the presence of Voice call

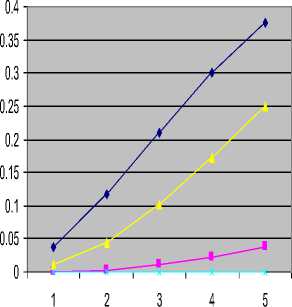
The scenario when time threshold (t e ) is applied to the HD is given in Fig. 16; thus, the blocking probabilities is further. Reduced. The reason for the slight reduction in the blocking probabilities is the presence of voice traffic and Handoff data traffic. The voice traffic will always have preference over the data traffic since data traffic can usually tolerate some degree of service degradation while voice is more delay sensitive [17]. Also, the threshold is only applied to the handoff data; therefore the effect of this is not too significant when compared to the overall probabilities.

Data traffic blocking probabilities when there is no voice traffic in q 2 is shown in Fig. 17. This shows that there are more channels available for the HD users in q 2 , this account for the further reduction of blocking probabilities of data traffic in the cell. There is further reduction in blocking probabilities when time threshold (t_e) was applied to the HD traffic though the t_e was only applied to HD and number of HD are always minimal.

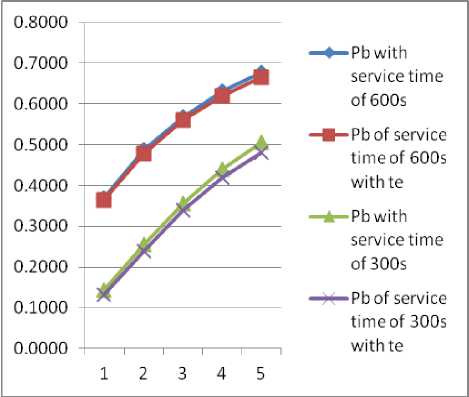
Fig.16. Graph representation of Data traffic probabilities in the presence of Voice call when te was applied

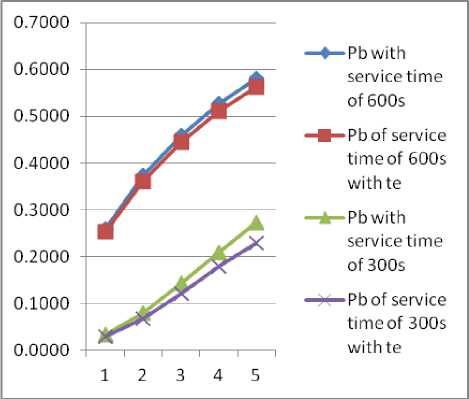
Fig.17. Data traffic without voice

• XI.    Conclusion

This work proposed a Multi-level access priority model to manage calls on the network in other to reduce congestion on the network. It is shown through analytical simulation that the model proposed in this work reduce congestion better than the traditional Erlang B which is in use presently in GSM networks because of its ability to classify calls into different classes and prioritize them according to the nature of their service. The work also show sthat, when applied a time-threshold to handoff calls, more new calls are accommodated thereby reduce Network congestion further.