Multi-Objective Memetic Algorithm for FPGA Placement Using Parallel Genetic Annealing

Published Online April 2016 in MECS

Reconfigurable computing involves computation using high performance hardware that can adapt to changing computational requirements, with software flexibility. Reconfigurable computing involves the use of reconfigurable devices, such as FPGAs, for computing purposes. FPGA has gained its popularity in implementing digital circuits because of low cost and fast prototyping. The correct placement of logical blocks in FPGA is an optimization task, which involves multiple objectives. The placement problem [1][2][3] deals with finding certain locations for each cell on the entire layout such that it minimizes the certain objective functions subjected to certain constraints imposed by the designer. Given a set of m modules, M = {M1, M2, …, Mm}, a set of n nets N = {N1, N2, …, Nn}, and a set of p primary input pins and primary output pins R = {R1, R2, …, Rp}, associate with each module Mi∈ M a set of nets NMi where NMi⊆ N. Similarly, associate each net Ni∈ N to a set of modules MNi where MNi= {Mj| Ni ∈NMj}. Given a set of locations L = {L1, L2, …,Lk}, where k ≥ n. The placement problem is defined as follows:

• • To assign each M i ∈ M to a unique location Lj such that the objective functions are optimized.

Usually each module is considered to be a point, and if M i is assigned to location Lj then it’s position is defined by the coordinate values (x j , y j ).

The placement problem is NP-complete problem. The Placement of FPGA is a Multi-Objective Optimization Problem which primarily involves minimization of three or more objective functions. The Presence of multiple objectives in a problem gives rise to a set of optimal solutions largely known as Pareto-optimal solutions, instead of a single optimal solution. In the absence of further information, one of these Pareto-optimal solutions may not be better than the other. Thus, treating the placement as multi-objective one and finding multiple pareto-optimal solutions allows the designer to have a deeper understanding of the problem and its optimal solutions. In this paper, we propose a combination of Multi-Objective Optimization algorithm and Simulated Annealing technique to solve the placement problem. The Algorithm divides the FPGA blocks into clusters, then each cluster executes Non Dominate Sorting Genetic Algorithm (NSGA-II) [10][12], a most widely used multi-objective optimization algorithm in parallel for each cluster. Further, the best solution of each cluster is migrated to other clusters if required, based on the migration coefficients using fuzzy logic.

The process is repeated until the termination criteria are met. Eventually, the best solution is chosen based on the requirement. Simulated annealing is used for further improvement of the best solution chosen .

The paper is organized as follows: In Section II, the existing algorithms to solve the placement problem is discussed. In Section III, the multi-objective optimization and NSGA-II are explained. In Section IV, the proposed algorithm is elucidated. In Section V, the experimental results and graphs are analyzed and Section VI concludes our work.

• II.    Existing Algorithms

Placement is usually separated into global and detailed placement. Global placement algorithms [17][18] include analytical techniques whereas detailed placement uses various kinds of local optimizations. Some of the placement techniques in the literature have been discussed in this section.

The first one is Genetic algorithm [1][3][4]: The algorithm starts with an initial set of random solutions termed as population. Each individual in the population consists of a string of bits termed as genes. The chromosome, which is made up of genes, represents a solution to the problem. At each generation, the individuals in the current population are evaluated using fitness function. These individuals with high fitness values, i.e. good placement solutions, are more likely to be selected and genetic operators such as crossover and mutation are employed to find a good solution. As a result, the fitness of population evolves as the number of generation increases. Different types of genetic algorithms with different combination of selection and crossover operators have been used in literature.

Second one is Simulated Annealing [1][6][9]: The algorithm starts with random initial set of solutions and initialization of high temperature. Perturb the solution with a defined move, and the change in value due to the corresponding move is calculated, depending on which acceptance or rejection of the corresponding move is to be decided. The temperature value is updated by lowering the temperature and repeat the process until the freezing point is reached.

Third one is Parallel Genetic Algorithm (PGA)[5][21]: The algorithm divides the FPGA into different clusters and then genetic algorithm is applied parallel to each cluster. The best solution from one cluster is sent to the other by using migration technique. Different approaches of PGA such as the master-slave approach, Grid approach, parallel simulated annealing approach, etc., have been used in literature.

Fourth one is Genetic Annealing Technique [7][9]: The genetic algorithm is applied over a period of generation and then the best solution is chosen. Simulated annealing is used for local optimization.

Fifth one is the Stochastic Tunneling Approach [13]: The Dynamically adaptive stochastic tunneling (DAST) algorithm is to avoid the “freezing” problem commonly found when using simulated annealing for circuit placement on field programmable gate arrays (FPGAs). The placement is achieved by allowing the DAST placer to tunnel energetically inaccessible regions of the potential solution space. The existing solutions in the literature are compared and listed in Table 1.

Table 1. Comparison of Existing for FPGA Placement

ALGORITHM	ADVANTAGES	DISADVANTAGES
Genetic Algorithm (GA)	The algorithm works over a population of solution and is based on natural selection, therefore with fitness function the search is guided to find the optimal solution.	Sometimes it may get stuck in local minimum and may not yield the global solution. It is slow process. For large problem, the determination of the optimal solution may take considerable amount of time.
Simulated Annealing (SA)	It is comparatively much faster than the genetic algorithm.	It does not yield the exact global solution but solution near to the global solution.
Parallel Genetic Algorithm (PGA)	Comparatively much faster than the both, genetic algorithm (GA) and simulated annealing (SA). The number of iterations is much lower.	Synchronization and migration problem exist, because of which it may not give better solution. Fixing the migration rate as constant may hinder the performance of the algorithm.
Genetic Annealing (GASA)	Yields a much better and quality solution as compared to the other algorithms.	The number of Iteration becomes too higher which degrades the performance of the algorithm .

• III.    Multi-Objective Optimization and NSGA-II

Classical optimization methods suggest converting the multi objective optimization problem to a single-objective optimization problem by emphasizing one particular Pareto-optimal solution at a time. This is done by the weighted sum or ɛ-constraint approach. Although it is argued that the conversion of the multi objective problem to a single objective can find pareto-optimal solution but there are few drawbacks. First, the multiple applications may not always produce different optimal solutions. Second, uniformly distributed set of pareto-optimal solutions may not be found i.e., better spread of solution may not be obtained. Thus, multi-objective optimization are computationally faster and ideal for finding well distributed set of pareto-optimal solutions.

In the proposed algorithm, NSGA-II[10] is used for the multi-objective optimization. Our problem is a three objective optimization problem where we have to place the logical blocks of FPGA such that the following goals are achieved:

• •    Critical path or the time for mapping is minimized.

• •    The power consumption of the programmable routing is minimized.

• •    The overall wire-length of the mapped circuit is minimized.

In NSGA-II[10][12], the offspring population Q t is created from the parent population P t , by using normal genetic operators like selection, cross-over, and mutation. P t and Q t are combined to form a new population R t of size 2N. Further, NSGA is used to classify the entire population R t and the new population is filled by solutions of different non dominated front at a time. The filling of solutions starts from the order of best non-dominated front, the next and so on. Since only N slots have been occupied from the 2N slots of the population R t , the rest of the solution that cannot be accommodated in N slots are discarded. When the last allowed front is to be considered, there may be more solution in the front than the solution to be accommodated. Instead of arbitrarily discarding some members from the last front, the solution that makes diversity of the selected solution highest is chosen. This is done by crowded distance sorting approach.

• IV.    Proposed Algorithm and Methdology

The Proposed algorithm shown in Figure I combines the Parallel NSGA-II and the Simulated Annealing (SA) approach such that it yields a quality and faster solutions as compared to the existing algorithms. Initially, the algorithm divides the FPGA blocks into clusters. Further, each cluster executes NSGA-II, in parallel for each cluster. Within each cluster, the algorithm treats each individual as an active entity or a process. Each process communicates with every neighboring process. To perform selection, each process sends its fitness value to every neighboring process, and then waits to receive either a specified number of communications from neighboring individuals, or a new individual to replace itself. If a process receives information from neighboring individuals, both selection and mutation are done without the knowledge of the other processes. The resulting children are combined with their respective parents and the non-dominated sorting is applied on them to identify different fronts. The best children are selected from the best front, then next and so on. These children replace the parents and a new generation begins.

Mutations are also done such that it converges to global solution quickly. The best solution of each cluster is migrated to other clusters if required based on the migration rate determined using fuzzy logic. These steps are executed in parallel for each cluster until the value stabilizes over a period of generations or the termination condition is met. Finally, from the set of pareto-optimal solutions obtained, the best solution is selected based on the requirement and simulated annealing is done for further improvement.

• A.    Chromosome Representation

The first and foremost step in the encoding process is to identify each member of the population uniquely and distinctly. The proposed algorithm uses a different type of chromosome representation [12] as compared to the traditional approach. The two dimensional array of

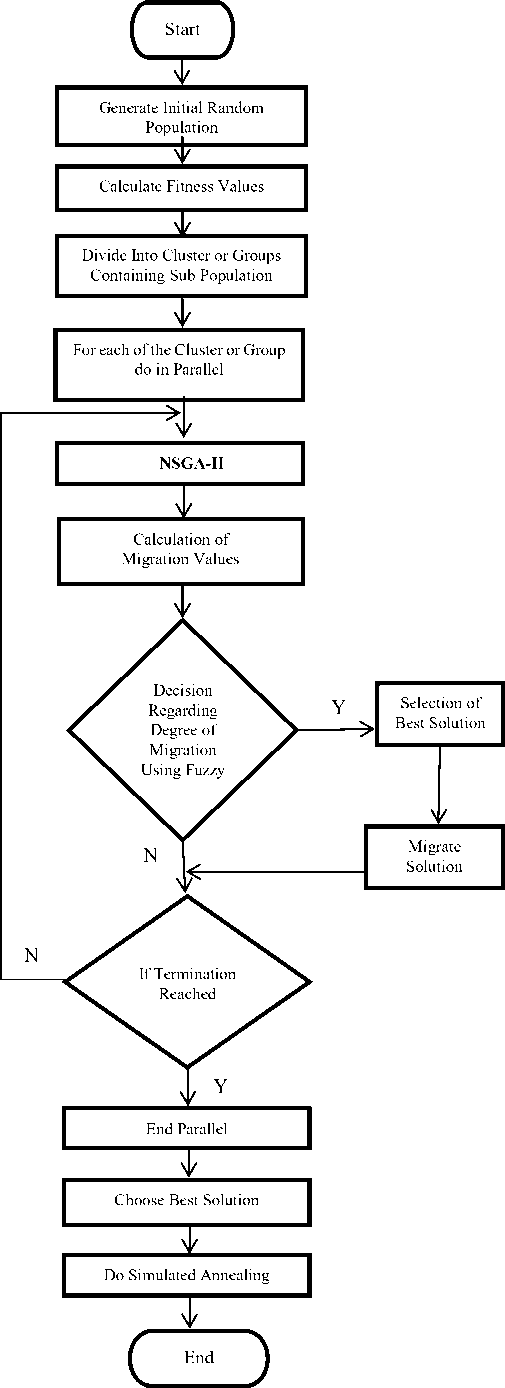
Fig.1. Flowchart of the Proposed Algorithm

components are represented by one dimensional array by one dimensional array by using left to right scan performing in a top to bottom fashion. This way we have n-element string of integers representing different component. In this representation, the ith position from left of the string, an integer between 0 and (i-1) is allowed. The String is decoded to obtain the placement as follows, the ith position denotes the placement of component ‘i' in the permutation.

The decoding starts from left most position and proceeds serially towards right. When decoding ith position, the first (i-1) components are already placed, by providing with ‘i' place holders to position the ith component. The advantage of this type of chromosome representation is that simple cross-over and mutation operators are used. This reduces the complexity of the code.

For example, consider six components (p-u) to be placed on a 3X2 array. Consider a random string which denote a solution, (0 0 2 1 3 2) then by decoding using the above method we get the following permutation (q s u p t r) corresponding to the above string. On converting to two dimensions, it is represented as follows:

q	s	u
p	t	r

• B.    Fitness Functions

The proposed algorithm is implemented for optimization of three objective functions. The three objectives that are to be minimized are as follows:

• (i)    Cost Function for Wiring in Placement [3]:

Wiring Cost = N^q ( i ) *| bbx ( i ) + bby ( j ) ]

«                          (1)

where N is the Number of Nets, bbx(i) and bby(i) are the x and y dimensions of a bounding box for each net(i), and q(i) denotes scaling factor for better wire-length estimates.

• (ii)    Cost Function for Timing in Placement [3]:

Timing Cost = ^Delay(i, j)*Criticality(i, j)*CE where CE denotes Constant, Delay(i,j) indicates the delay of the connection from source ‘i' to destination ‘j’, Criticality (i, j) denotes the measure of how close the given i, j path is to the global critical path.

• (iii)    Cost Function for Power in Placement [3]:

N

Power Cost = ^ q ( i ) * |2 bbx ( i ) + bby ( j ) ] * Activity ( i ) i =1

where activity(i) denotes the switching activity on a particular net, and by reducing this component, the power consumed over long and programmable routing lines are reduced.

• C.    Migration Problem

The main problem in Parallel Genetic Algorithm is constant migration rate. Generally, the individuals of migration are almost the best individuals in each sub-population, so if the migration rate is set to a constant, then a high migration rate would lead to the spreads of advance individuals in all population and improves the speed of convergence. However, at the same time it decreases the population diversity. Its drawbacks are to explore different regions of the search space. On the other hand, setting a low migration rate would affect the performance of the algorithm drastically by spreading of individuals which have not fully evolved. Since we use the non-dominated sorting genetic algorithm parallel for each cluster in our proposed algorithm, we need to solve the migration problem as it's a major concern affecting the performance of the algorithm. Therefore, the migration problem is solved in our proposed algorithm by not setting the migration rate to constant, but instead it is tuned by fuzzy rule according to states of each subpopulation.

• D.    Fuzzy Logic

In the proposed algorithm, the migration rate is decided by fuzzy rule[14][15][16] based on the average fitness value f ai and the difference between the maximum and average fitness value (f mi -f ai ) in each cluster ‘i'. Depending on these two variables (f ai , f mi - f ai ), we are able to understand the states of each island (early stage or final stage). In the process of the migration, some individuals in sub-population with the advanced evolutionary condition are easy to spread in all population. On the contrary, some individuals in sub-population with the delayed evolutionary condition are difficult to spread in whole population under the tuning of fuzzy rule. So the fuzzy rule plays a good part in guiding the evolutional direction for improving the quality of solution effectively.

Table 2. Fuzzy Rule Application

f ai /f mi - f ai	FS	FM	FL
DS	EVL	ELL	ELS
DM	EL	EM	ES
DL	ELL	ELS	EVS

Table 2 describes the application of the fuzzy rule [14][16]. FS means the average fitness in an island is small, and it also means this island is in the early searching stage. The same to the FL, it means the average fitness in an island is large, and also means this island is in the final searching stage. On the other hand, the DS means the difference between the maximum and average fitness value (f mi - f ai ) in an island is small, at the same time it also implicate the individuals in this island is rather compact. The DL is difference between the maximum and average fitness value (f mi - f ai ) in an island is large. According to different states different parameter values such as EVL, EL,

ELL, etc., are set. This basically solves the above problem where the migration rate is not constant but is varied in accordance with the different states of an island .

• V.    Experimental Results

The Algorithm was implemented by Message passing interface (MPI) program. The Program is directly run on the test bed with hardware requirements consisting of 64-bit Linux machine consisting of Eight Processor (32 Cores) with 2.66Ghz with internal memory of 8GB and an NVIDIA GTX280 GPU running at 1.35GHz and with 2GB of on-chip memory. The Program was tested with large datasets . The Performance of Proposed Algorithm was tested using different set of MCNC benchmarked field programmable gate arrays. The results showed that the proposed algorithm gives better results in terms of number of iterations and CPU time than the various traditionally existing algorithms.

Parameter settings shown in Table 3 for NSGA-II and simulated annealing (SA) are chosen and tested for the certain benchmarks.

Table 3. Parameter Settings

Maximum no. of Population	500
Maximum no. of genes in each cluster	65
Probability of cross over	0.6
Probability of Mutation	0.01
α (percentage of attempted movements)	β
0.15 < α < 0.3	0.95
0.05 <= α <= 0.15	0.8

• A.    Comparison of CPU Times

The proposed algorithm effectively improves the quality of placement and achieves less CPU time as compared to the existing algorithms in all cases without degradation of performance in the final routing stage. Table 4 shows the comparison of the CPU times of the proposed solution with the existing solutions. Figures 2, 3, 4, 5 and results show that the proposed algorithm reduces the CPU time to an average of nearly 15% as compared to the Genetic Algorithm, 12% as compared to the Simulated Annealing, nearly 6% as compares to the Genetic Annealing algorithm (GASA) and nearly 4% as compared to Parallel Genetic Algorithm (PGA).

The X-Axis of the graphs represents the MCNC benchmarked FPGA’S in which the algorithm was tested and the Y-Axis represent the CPU Time for the placement of the blocks in seconds. The Figure 2 and Figure 3 shows the comparison of the CPU time of the traditionally exiting GA and SA with the proposed algorithm. The proposed algorithm gives better results mainly because of its parallel execution and the use of hybrid approach. Figure 4 shows the comparison of CPU times of the Genetic Annealing

(GASA) with the proposed Algorithm. The Proposed algorithm gives a much better results because of the use of NSGA-II and the Parallel approach. Figure 5 shows comparison of proposed algorithm with the parallel genetic algorithm. The Proposed algorithm gives better results as compared to most of the Parallel Genetic Algorithms because of the use of fuzzy logic to determine the migration rate instead of fixing it to a constant. This improves the performance of the proposed algorithm to a great extent.

Figure 6 shows the comparison between the CPU times of proposed algorithm with all the existing algorithms.

Table 4. Comparison of CPU Times of Proposed algorithm with the Existing Solutions

FPGA	GA	SA	GASA	PROPOSED
9symml	25.74	24.99	22.86	20.01
alu2	91.76	80.54	74.27	69.99
apex7	38.39	38.44	38.11	36.64
example2	107.5	99.02	95.23	92.87
pcler8	47.25	44.2	42.69	40.20
k2	461.5	450.2	364.7	358.7
term1	28.06	27.98	26.35	24.01
5xp1	64.59	62.22	58.23	56.66
e64	163.70	160.8	155.21	153. 22
too-lrg	82.51	80.42	74.37	72.66

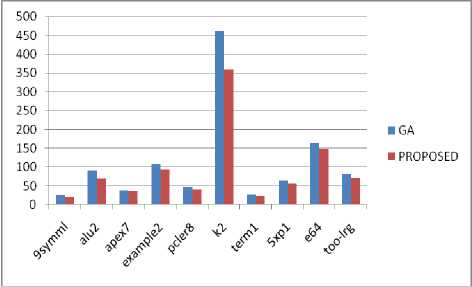
Fig.2. Comparison of CPU Times of Genetic Algorithm with the Proposed Algorithm

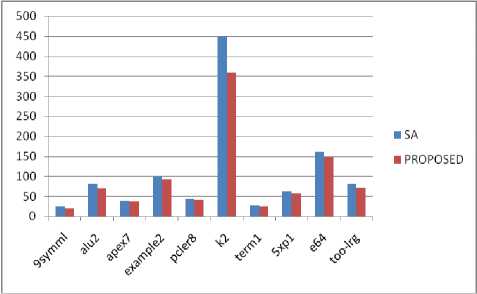
Fig.3. Comparison of CPU Times of Simulated Annealing Algorithm with the Proposed Algorithm

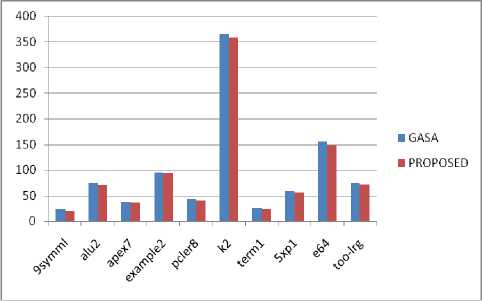
Fig.4. Comparison of CPU Times of Genetic Annealing Algorithm with the Proposed Algorithm

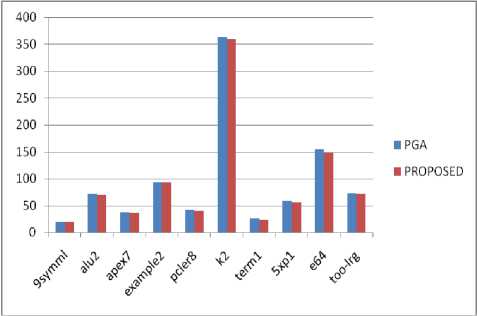
Fig.5. Comparison of CPU Times of Parallel Genetic Algorithm with the Proposed Algorithm

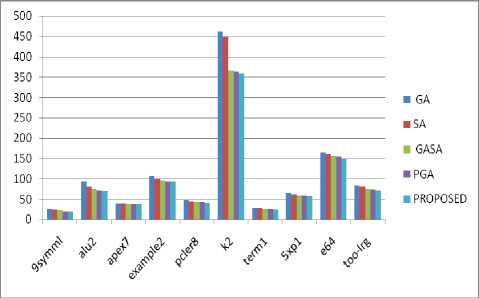
Fig.6. Overall Comparison

Thus, the analysis of the CPU times for various FPGA show that the proposed algorithm gives faster placements as compared to the existing traditional algorithms.

• B.    Comparison of Number of iterations

The proposed algorithm reduces the number of iterations as compared to the existing algorithms. Figure 7 shows the comparison of number of iterations of the proposed algorithm with the existing solutions. The proposed algorithm reduces the number of iterations to nearly 50% as compared to the Genetic Algorithm and the g enetic a nnealing algorithm . t his is mainly due to the parallel approach and the use of NSGA-II.

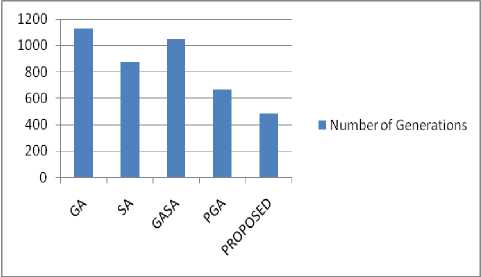
Fig.7. Comparison of Number of Iterations

• C.    Quality of Solutions

The proposed algorithm also gives better spread of solution and quality solutions as compared to the existing solutions. This is mainly achieved due to the use of Non-Dominated Sorting Genetic Algorithm (NSGA-II).

• VI.    Conclusion

Since the algorithm uses parallel approach, the determination of migration coefficient is an important factor affecting the performance of the code. This problem is solved by using fuzzy logic. Since it uses NSGA-II for Multi-Objective Optimization it finds better spread of solutions and it also gives quality solutions. The proposed algorithm uses different chromosome representation which makes it possible for the usage of simple crossover and migration operator, as compared to all existing algorithm. It also reduces the complexity of the code. The further final optimization of best solution using Simulated Annealing gives the best solution.

Results and graphs show that the proposed algorithm is better than the existing algorithms in terms of CPU time and the number of iterations and the quality of solutions obtained.

As a part of future research, the algorithm can be tested with various different mating and selection operators to achieve more efficiency and speed. The algorithm can also be modified to determine the crossover and the mutation rate by using the fuzzy logic. This may further improve the performance of the proposed algorithm.