Multi-objective monkey algorithm for drug design

Published Online March 2019 in MECS

Optimization problems can be solved using various techniques. Earlier, they were solved using mathematical or exact methods such as divide and conquer, back tracking, dynamic programming etc., which provides a single solution in polynomial time. However, many real-life NP-hard complex problems remain unsolved. These complex problems can be solved by bio-inspired algorithms such as evolutionary algorithms (e.g. genetic algorithm), swarm intelligence algorithms (e.g. particle swarm optimization, ant colony optimization, bacterial foraging algorithm, etc), or with the help of physics based optimization algorithms (ray optimization algorithm, big-crunch and big bang algorithm, joint operations algorithm, gravitational search algorithm, etc).

Bio-inspired algorithms mimic the living organisms’ unique behaviors to solve day-to-day problems. Bioinspired algorithms can also be classified under artificial intelligence techniques, as they are based on the intelligent behaviors of the living organisms. Living organisms perform normal and easy to do activities when they are alone; however, when they come together in a group, they exhibit interesting, intelligent and productive activities to solve more complex issues. Swarm intelligence algorithms are based on the behavior of group/colonies of birds, animals and insect behaviors and intelligence. Well known examples are ant colony behavior, birds or fish swarms behavior, bee colony behavior, bacterial foraging behavior and grey-wolf behavior. In this paper, the behavior of monkeys (mountain and tree climbing, jumping, watching and somersaulting) is harnessed to solve complex optimization problem in the field of Computer-Aided Drug Design (CADD).

Monkey algorithm [1,2] is one of the bio-inspired algorithms, which simulates the behaviors of monkeys such as climbing, jumping, watching and somersaulting over the mountains during their search for food. Unfortunately, the original monkey algorithm is not suitable for the multi-objective optimization problems. Multi-objective optimization [3] (multi-criteria or multiattribute optimization) is defined as the process of simultaneously optimizing more than one objectives that are to be either maximized or minimized. There are some problems where the optimization of the first objective leads to the optimization of the other objective automatically. But most of the real world multi-objective problems have objectives with set of constraints in which the optimization of one objective leads to the degradation of the other objectives. This is particularly true in the field of drug design.

In this paper, a multi-objective monkey algorithm (MOMADrug) is applied to the interdisciplinary problem of de novo drug design (DNDD) [4]. DNDD is a computer-aided drug design technique to find optimal solutions using multiple objectives and compared with the already reported work, MoGADdrug. This paper is organized as follows: Section 2 discusses about the related works from the literature, Section 3 describes monkey algorithm in detail, section 4 discusses the DNDD in detail and section 5 describes the proposed monkey algorithm for the multi-objective optimization for DNDD. Section 6 gives the implementation process and section 7 shows the experimental results of MoMA for DNDD and compares the results with the previously described multi-objective GA for DNDD [5]. Finally, section 8 concludes the paper.

• II.    Related Works

Many single objective optimization algorithms to solve the real-time optimization problems are reported in the literature. Particle swarm optimization [6], Firefly algorithm [7], Whale optimization algorithm [8] are some examples. Particle swarm optimization algorithm simulated the intelligence of swarm of birds. Firefly algorithm is a meta-heuristic algorithm based on the bioluminescence behavior of the fireflies used for communication. Whale optimization algorithm is based on the behavior of the humpback whales. Popular multiobjective algorithms include NSGA-II [9], MOPSO [10] and MOGWO [11]. NSGA-II is one of the multiobjective version of genetic algorithm with an archive, and features such as non-dominated sorting and crowding distance calculation to obtain the non-dominated optimal solutions. MOPSO is the multi-objective version of particle swarm optimization algorithm. While, multiobjective grey wolf optimizer (MOGWO) has an archive to store the non-dominated solutions and features like leader selection with a grid mechanism to improve the contents of the archive. For the de novo drug design, various multi-objective optimization techniques such as evolutionary graphs [12], Pareto algorithm [13], genetic algorithm [14] are recently reported. Apart from these, we have also extensively reviewed various evolutionary techniques used for de novo drug design [4].

• III.    Monkey Algorithm

The monkey algorithm proposed by Zhao et al.[1], was designed after the inspiration from the mountain climbing behavior of monkeys. Mountains with varying heights in a field with good sources of food constitute the problem space for this algorithm. The monkeys migrate in groups to search for food over the mountains. In the food searching process for their group, they perform climbing, watching, jumping and somersaulting. The three basic processes involved in the monkey algorithm namely, Climb, Watch-Jump, and Somersault are explained below:

• A.    Climb process

Usually monkeys starting from their initial position climb over the mountain step-by-step carefully. This behavior is simulated in the climb process of monkey algorithm to search for the local optimal solution based on the pseudo-gradient (PG) information [15] of the objective function. Step length plays an important role in incrementing the monkey positions and covering the local search space completely. Step length parameter is used to define the distance covered by each step of the monkey to move its position during the climb process as A ( x i ) = ( A x i 1 , Ax i 2 ,... A x in ) where,

A x ij = a and - a with a probability 0.5 of each (1)

where j = 1,2,... n respectively. Then the Pseudo gradient (PG) of the objective function is calculated. New position of the monkey x new is obtained from the equation (2).

x new = x ij + step _ length * PG         (2)

• B.    Watch Jump process

After carefully climbing up the mountain and reaching the mountain-top, the monkeys will watch around from the mountain-top. Eyesight parameter (es) (field of vision) is used to define the maximum distance that the monkeys can watch. Using the eyesight parameter, generate x min and x max as

• x min = x ij — es and x max = x tj + es         (3)

During the watch process, within the field of vision, if any mountain higher than the current monkey position is observed, it will jump to that adjacent mountain and this position is updated as the new position ( xnew ij ) of the monkey. Then from the new position, monkeys continue to climb up by taking the x new as the initial position.

• C.    Somersault process

To introduce monkeys to new global search region, the somersault process is utilized. In somersault process, the barycenter from the current positions of all monkeys, called the somersault pivot ( SP ) is selected. The monkeys will somersault to a new position either forward or backward with respect to the pivot. Somersault interval ( alpha ) is used to govern the maximum distance the monkey can somersault. This process ensures new solutions in the fresh search space.

monkey _ new _ position = x y + alpha * ( SP - x y ) (4)

In monkey algorithm, the highest mountain-top reached by a monkey is taken as the optimal value of the objective function. These three processes - Climb, WatchJump, and Somersault are executed for a predefined number of cycles called the cycle number to reach the highest mountain-top by the monkeys, which is actually the optimal solution of the monkey algorithm. In this paper, the single objective monkey algorithm reported by Zhao et.al.[1], is modified to solve multiple objectives using the pareto-dominance concept for de novo drug design.

• IV.    De Novo Drug Design (DNDD)

Computer aided drug design (CADD) is a technique to design new drug molecules easily and cost effectively with the help of computer programs. The term ‘de novo’ in Latin means ‘from the scratch’, ‘a new’ or ‘from the beginning’. De novo drug design (DNDD) is a CADD technique in which the drug-like molecules are designed from the scratch or from the beginning. DNDD is a combinatorial optimization technique with a huge chemical space as the problem space, from where the drug-like molecules or the optimal solutions need to be arrived. There are two methods used for the design of drug-like molecules in DNDD;

• (i)    Atom-based method in which the molecules are constructed in an atom by atom manner and

• (ii)    Fragment-based method in which small fragments are used as the building blocks for the construction of the molecules.

In this work, the fragment-based molecule construction method is chosen to carry out DNDD. A newly designed drug using DNDD is considered suitable for testing in experiments when it possesses drug-like properties such as good oral-absorption capability. The objective functions used in DNDD include similarity to a reference molecule and oral-bioavailability score (OBA); OBA score includes molecular weight, hydrogen bond acceptors, hydrogen bond donors and XlogP values of the designed molecules. As there are more than one objective in the DNDD problem, it is categorized as a multiobjective optimization problem.

• A.    Multi-objective optimization in de novo drug design

Stochastic optimization algorithms are classified into either single or multi-objective optimization algorithms depending upon the number of objectives used in the problem. In a multi-objective optimization problem which has more than one objective, y i = f i ( x ) where i = 1,2,... m objectives, that need to be simultaneously optimized.

In real world, most of them are multi-objective optimization problems, such as DNDD. For solving multi-objective problems, there are three commonly used methods as described by Konak et al. [16]. They are:

• 1.    Weighted sum approach: In this approach, each objective function is provided with a weightage so that the multi-objective optimization problem is reduced to a single objective problem, making it easy to solve.

• 2.    Altering objective functions: In this approach, various objective functions alternating randomly between generations or the population is divided into subpopulations and different objective functions are used in every sub-population.

• 3.    Pareto-ranking approach: In this approach, the complete population is ranked based upon the dominance rule and then each solution is given a fitness value depending upon their rank within the population instead of their original objective function value.

In the multi-objective de novo drug design, optimal solutions are obtained by evaluating more than one objective or fitness function that needs to be maximized. In this work, dominance is used to evaluate the quality of the optimal solutions [17]. Among two decision vectors A and B,

A is said to strictly dominate B if f i ( A ) <  f i ( B ) for all i = 1,... D and f i ( A ) <  f i ( B ) for some i ; less stringently A weakly dominates B (denoted A &  B ) if f i ( A ) <  f i ( B ) for all i . A set of decision vectors is said to be a nondominated set if no member of the set is dominated by any other member. The true Pareto front, P, is the nondominated set of solutions which are not dominated by any feasible solution. The objectives or the parameters that need to be optimized in the DNDD are tanimoto similarity and oral bio-availability; they are discussed in detail in the section below.

• B.    Objectives of de novo drug design

• 1)    Tanimoto Similarity

Tanimoto similarity score is a popular similarity measure to compare the similarity between chemical structures. In tanimoto similarity, chemical structure similarity between a test and a reference molecule is evaluated using fingerprint methods; for example using daylight fingerprints [18]. The tanimoto similarity score ranges from 0 to 1; where, a score of 1 represents similar structures and 0 represents no similarity between the test and the reference molecule. The two chemical structures are usually considered quite similar if tanimoto similarity coefficient is >0.85 (for Daylight fingerprints).

• 2)    Oral Bioavailability Score

Oral bio-availability (OBA) score measures the ability of the designed molecules to be absorbed into our systemic circulation after administration through oral route. As it is desirable to design orally available drugs (so that they can be taken as tablets, capsules, etc), incorporating OBA score as one of the objective function of DNDD helps to design better drug-like molecules. OBA score for a molecule is determined by calculating the molecular weight, hydrogen bond acceptor, hydrogen bond donor, and the XLogP values of the molecules. OBA score is based on the ‘Lipinski’s rule of five’ (Ro5) [10, 11]. The Ro5 states that a molecule is orally bio-available and is drug-like if it satisfies the following four conditions:

• •    The number of hydrogen bond donors do not exceed 5

• •    The number of hydrogen bond acceptors do not exceed 10

• •    The molecular weight is not more than 500

Daltons and

• •    The octanol-water partition coefficient (LogP)

value is not greater than 5

That is, for calculating the OBA score, we are using four different objective functions (parameters) -molecular weight (MW), hydrogen bond acceptor (HBA), hydrogen bond donor (HBD), and the XLogP (XLP) values – calculated from the designed molecules. In this paper, the OBA score is calculated based on the previously reported method [14]. Here, each of the four parameters in the Lipinski’s rule of five (Ro5) is given a weightage of 0.25, resulting in a total weightage value of 1 for the OBA score. Thus, a designed molecule that satisfies all the four parameters of Ro5, will have an OBA score of 1. However, if the designed molecule doesn’t satisfy one or more of the four parameters of Ro5, it will have an OBA score of <  1 . Together with OBA score and Tanimoto similarity coefficient, the fitness of the potential solution obtained during the traversal of the monkey in the search space is determined. The algorithm for the calculation of the OBA score is given below.

Start

Initialize the OBA_score variable

Check the values of Hydrogen bond donors (HBD), Hydrogen bond acceptors (HBA), Molecular weight (MW) and XLogP partition coefficient (XLP).

If HBD <= 5 then OBA_score = OBA_score + 0.25 If HBA <=10 then OBA_score = OBA_score + 0.25 If MW <= 500 then OBA_score = OBA_score + 0.25 If XLP <= 5 then OBA_score = OBA_score + 0.25 End

The fitness score is represented as equation (5) in MoMADrug.

Fitness score = [Tanimoto similarity score, Oral Bioavailability score]               (5)

• V.    Proposed Multi-objective Monkey Algorithm

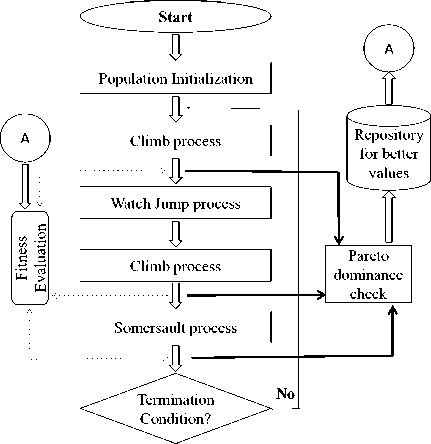
The proposed multi-objective de novo drug design provides optimal solutions (molecules) by evaluating more than one objective or fitness function to be maximized. New molecules are designed from the fragments taken from the commercially available drug molecules. The objective functions are the Tanimoto similarity which provides the similarity of the designed molecule with respect to the reference molecule and the oral bio-availability score that provides the score about the drug absorption. Fig.1 shows the flow chart of the proposed multi-objective monkey algorithm for de novo drug design.

A. Design of multi-objective monkey algorithm for de novo drug design (MoMA)Drug)

The design of MoMA for DNDD is discussed in two stages. First, the basic monkey algorithm design with standard parameter values and then tuning of the parameters to improve the quality of the solutions obtained.

Yes

Optimal Solution/(s)

End

Fig.1. Flow Chart of Multi-objective Monkey algorithm

• 1)    Representation of drug fragments

The fragment library is constructed using the acid, amine and double amine drug fragments extracted from approved drugs. A total of 28 acids, 162 amines and 19 double amine fragments were used in constructing the fragment library, as reported earlier [21]. In the monkey algorithm, the drug fragments were assigned a range of position values in all the x, y and z axes. The monkey positions (representing solution or molecule) were generated from this range of fragment resource values.

• 2)    Initial population generation

In the standard monkey algorithm, a population of 100 monkeys or agents are generated in a random manner, either in the 2D or 3D solution space. 2D monkey position consists of acid and amine fragment position values in x and y axis, while a 3D monkey position consists of acid, double amine and acid fragment position values in x, y and z axis, respectively. For each monkey’s initial position, two position values ranging from a minimum of 0 to a maximum of 80 are selected. These two values represent the allowed position of the monkeys in the x, y and z axes. For example, if the generated value is [72.8690, 31.6532], the initial position of the monkey in the x axis is 72.8690, representing an acid fragment and the position in the y axis is 31.6532, representing an amine fragment for the 2D monkey. Similarly, for a 3D monkey with a value of [41.6526, 22.6469, 19.8668], the initial position of the monkey in the x axis is 41.6526, representing an acid fragment, the position in the y axis is 22.6469, representing a double amine fragment and the position in the z axis is 19.8668, representing an acid fragment. Fig.2 shows a representative 2-dimensional and 3-dimensional monkey positions in the search space and the corresponding solutions (molecule).

Representative 2D and 3D monkey positions

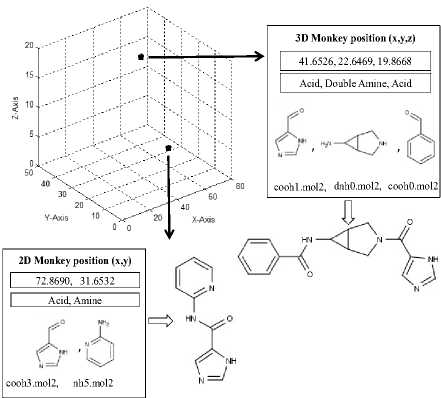
Fig.2. Solution representation in MoMADrug

For tuning the MA parameters for multi-objective DNDD, 100 monkeys are initialized to positions between (0, 0) to approximately 10% of the entire problem space (i.e.) (80, 80) with the destination point defined at (820, 820) or (820,820,820) depending upon the 2D or 3D positions.

• 3)    Climb process

In the climb process, the position of the monkey is changed in a step-by-step manner by using a step length parameter of 0.001 and a climb number of 100. The new monkey position after a climb process is represented by Equation (2). During the fine tuning of the climb process, a new parameter step _ size was introduced. For this, a random value from 0 to 2 was generated for each monkey and multiplied with PG as shown in equation (6), to generate the new monkey position. Hence, a randomly generated step size of 1.279 for a monkey makes the monkey to climb up with 1.279 units of PG .

x new = x ij + step _ size * PG (6)

• 4)    Fitness function evaluation

After the climb process, every monkey is now at its current best position. Then the fitness of the current position is calculated using the objective functions of the de novo drug design, i.e tanimoto similarity and oral bioavailability score. For each monkey, using the objective function values, pareto-dominance is calculated. From this, the non-dominated better solutions are stored in a repository or archive for future reference. When the repository is full, Roulette wheel selection method is used to select the monkey that has to be deleted from the repository.

• 5)    Watch-Jump process

After the climb process and fitness function evaluation, the monkeys from their corresponding higher mountaintops watch for better adjacent mountains and jump to them. The Watch-jump process is aided by an eye sight parameter value of 0.5, followed by successive climb processes to exploit the local search space. Then, using the new monkey position at the end of the watchjump process, fitness evaluation is carried out and a maximum of the non-dominated solutions from this process are stored in the repository, by replacing the older ones with better ones. The eye sight parameter used in the watch-jump process was tuned by changing to a value of 2% of the problem space, i.e. 16.0, to improve the exploration of the monkey along different directions.

• 6)    Somersault process

In the somersault process, using the barycenter of all the monkey positions, pivot value is derived. Using this pivot value, monkeys perform somersault process to explore the global search space. After the somersault process, fitness evaluation is done again and the repository is updated with the non-dominated members.

• 7)    Termination condition and output of MA

The above mentioned 3 processes (climb, watch-jump and somersault) are repeated for a predefined cycle number and then terminated once the cycle number is exhausted. Finally, the resultant molecule/(s) is written to the drive using the mol2 writer of the Chemistry Development Kit (CDK). The Marvin Sketch software is used to view the structure of the molecule written in mol2 format.

• VI.    Implementation Details

The object-oriented programming language Java and MATLAB were used for the implementation of the MA. The fragment library of 28 acid, 19 double amine and 162 amine fragments were used for designing the new druglike molecules. New molecules were generated by making linear connection between the acid fragment as the first part and the amine fragment as the second part for the individuals in 2D space. In the 3D space, acid fragment, double amine fragment and then an acid fragment are linearly connected using the Chemistry

Development Kit (CDK) library. The fitness values (tanimoto similarity and OBA score) were evaluated using the CDK library. Fragment library, reference molecule and newly designed molecule outputs are stored/ written in MOL2 file format. The MOL2 files were read using Marvin Sketch chemical structure drawing tool. The required Java archive files were imported into the MATLAB environment.

• VII.    Experimental Results

In the MOMADrug, a set of small fragments of acid, amine and double amine are taken in their .mol2 file format. Each drug-like fragment is assigned to a range of numeric values. Initial populations of monkeys are generated and are allowed to undergo the climb, watchjump and somersault processes. As the MOMADrug has to solve the two objectives for the drug-like molecules, the non-dominated solutions are stored in the repository iteratively. When the repository is full, the Roulette wheel selection is used to select the individual with low fitness values. CDK library is used to combine the fragments to generate the drug-like molecules based upon the non-dominated values. The optimal solutions are then visualized with the help of the Marvin Sketch tool.

In this section, tuning of parameter for monkey algorithm to optimize the search in the solution space is discussed first. This is followed by the discussion on multi-objective monkey algorithm as applied to the design of new molecules. Finally, comparison of the design results with that of our pervious multi-objective genetic algorithm (MoGADdrug) is discussed.

• A.    Parameter tuning for multi-objective Monkey algorithm

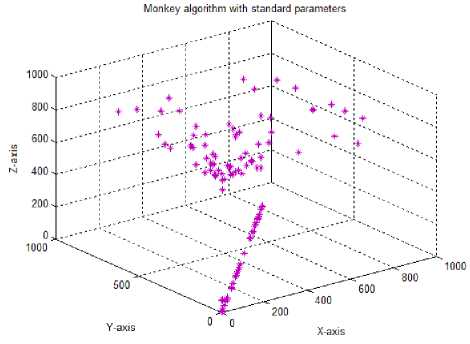
The original MA is designed to solve single objective optimization problems. In the process of designing a multi-objective monkey algorithm, it was found that the standard parameters needed some amount of tuning in order to explore the solution space thoroughly to obtain feasible solutions for applying it to the multi-objective optimization problems. The key parameters for MoMADrug are shown in Table 1 Parameters such as population size, initialization range, climb number, step length, eye sights were tuned and the solution search space coverage by the MoMADrug for the parameter tuning process is shown as 3D graph in Table 2.

The test case 1 in Table 2 shows the output graph obtained for the monkey algorithm with the following standard parameters: Initial population size of 100 monkeys, initialization range for the population being 10% of the total problem space, 10 cyclic number and 100 climb number for the monkeys. Step length is set at 0.001 and the eye sight parameter at a value of 0.5. While, the population size is fixed at 100 in all our test cases, as decreasing this number led to less exploration of search space by the monkeys. With the standard parameters, the graph shows that after 10 cycles the 2D solutions tend to move diagonally without covering x and y directions completely. Hence, each parameter was tuned to check the best possible parametric values for maximum coverage of search space by the MoMADrug algorithm.

Table 1. Parameters For Momadrug

Sl. No	MoMADrug parameters	Standard parameter values	New parameter values
1	Number of Monkeys/ Molecules	100	100
2	Step length	0.001	0.001 or 0.0001
3	Step size	-	Random between 0-2
4	Climb number	100	100
5	Eye sight	Between -0.5 and +0.5	Between -16.0 and +16.0
6	Somersault interval	(-1,1)	(-1,1)
7	Cyclic number	10	10
8	Source position (2D) Source position(3D)	Between (0,0) to (80,80) Between (0,0,0) to (80,80,80)	Between (0,0) to (80,80) Between (0,0,0) to (80,80,80)
9	Destination position (2D) Destination position (3D)	-	(820,820) (820,820,820)

In the second test case, the population initialization range was changed from 10% (standard parameter) of the problem space to entire problem space which is approximately equal to 820 in x, y and z axes. The results show that the solutions at the end of the MA cycle tend to be less spread out in the x, y and z directions for both the 2D and 3D solutions, thus decreasing the search space exploration capability. In the third test case, the effect of increasing the cyclic number to 100 from 10 cycles (standard parameter) is explored. At the end of 100 cycles, the monkeys didn’t not show improved spread in the solution space.

As the climb number plays an important role in the exploration of the local search space, in the fourth test case, the climb number was modified to 1000 from 100 (standard parameters). The output graph showed a good solution spread in the 3D search space. But the solutions in the 2D space were concentrated along the diagonal of x and y axis, implying lesser explorations along the x and y axes for the 2D solutions. In test case 5, the eye sight parameter for the watch-jump process was altered, to find comparatively better as well as adjacent solutions within the local search domain. Eye sight value was modified to 2% of the entire solution space which is 16.0. The resultant graph too showed a good spread of the 3D solutions than the 2D solutions in the search space.

The step length parameter in the standard monkey algorithm forces all the monkeys to move in tandem with the same step length. This is contrary to nature, where different monkeys will move with different step sizes and move to different lengths. Hence, in the test case 6, a new parameter called step size was introduced, which is a randomly generated number from 0 to 2 and used to alter the step length of each monkeys during the climb process. With this new step size parameter, the algorithm showed improvement with solutions moving in all the three directions for the given data set, however at the end of the

MA cycle the solutions in both 2D and 3D moved closer and showed lesser spread in the search space.

Table 2. Tuning of multi-objective monkey algorithm parameters

Test case-1 (Standard parameters): Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; Step length: 0.001; Eye sight:0.5; Xyz traversal: Nil

Test case-2: Initial population:100; Population range:100% of problem space; Cyclic number:10; Climb number:100; Step length:0.001; Eye sight:0.5; xyz traversal: Nil

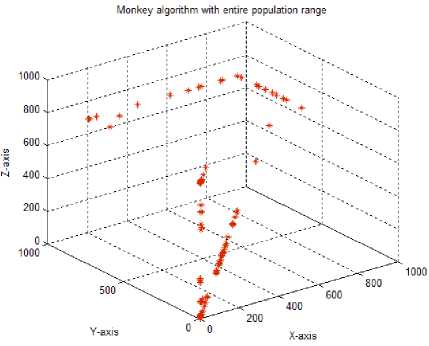
Test case-4: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:1000; step length:0.001; Eye sight:0.5; XYZ traversal:Nil

Test case-3: Initial population:100; Population range:10% of problem space; Cyclic number:100; Climb number:100; Step length:0.001; Eye sight:0.5; XYZ traversal: Nil

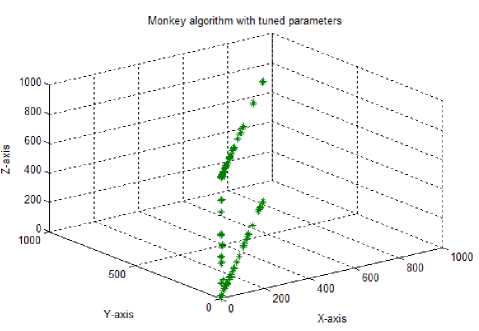
Monkey algorithm with tuned parameters

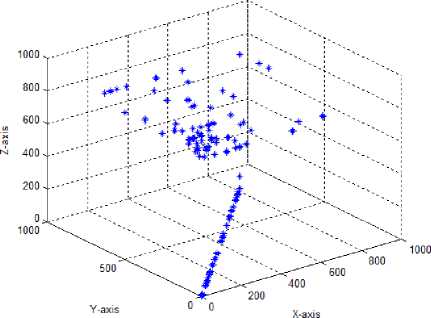
Test case-5: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; step length:0.001; Eye sight:2% of problem space; XYZ traversal: Nil

Monkey algorithm with tuned parameters

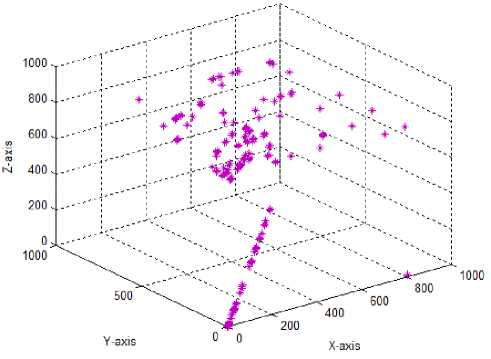
Test case-6: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; Step size: random between 0 to 2; Step length:0.001; Eye sight:0.5; XYZ traversal: Nil

Monkey algorithm with tuned parameters

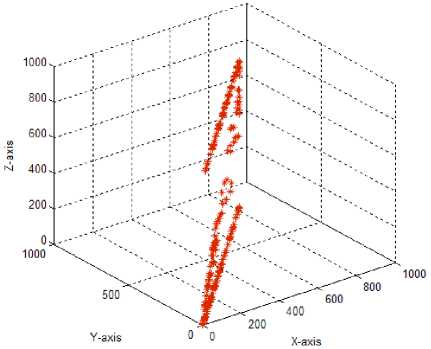
Test case-7: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; step length:0.001; Eye sight:0.5; XYZ traversal: Yes

Monkey algorithm with tuned parameters

Taxis           0 0             „ • л-axis

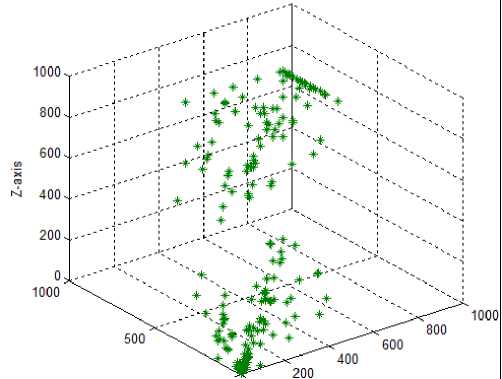
Test case-8: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; Step size: random between 0 to 2; Step length:0.001; Eye sight:2% of problem space; XYZ traversal: Yes

Monkey algorithm with multiple tuned parameters

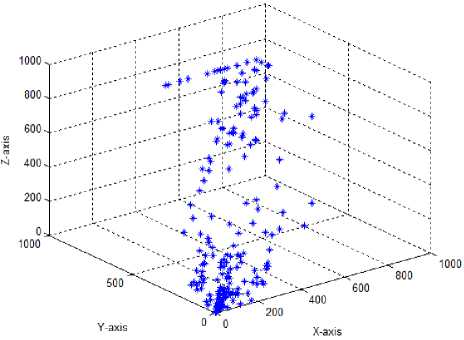
Test case-9: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; Step size: random between 0 to 2; Step length:0.0001; Eye sight:2% of problem space; XYZ traversal: Yes

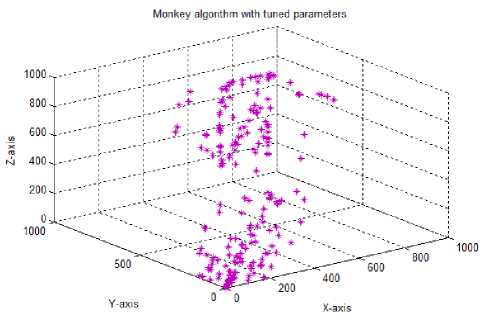
Test case-10: Initial population:100; Population range:10% of problem space; Cyclic number:10; Climb number:100; Step size: random between 0 to 2; Step length:0.0001; Eye sight:2% of problem space; XYZ traversal: Yes; Dominance concept: Yes

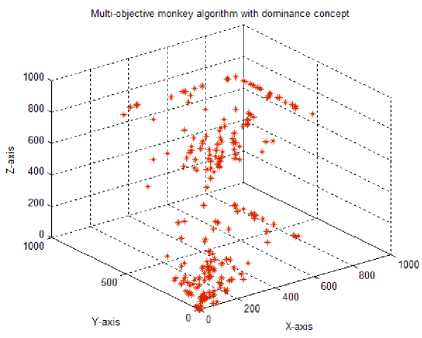
In the original monkey algorithm, the 2D monkey positions were moved by altering x and y axis (in the case of 3D monkey, x, y and z axis) values with the step length simultaneously. This resulted in lesser exploration of the search space, due to minimal traversal of monkeys along the x, y and z axis. Hence, in the test case 7, a new traversal along the x, y and z axis is proposed to improve the local domain search. For this, a random integer (0-2 for 2D monkeys and 0-6 for 3D monkeys) decision maker was used to decide on which axis of the search space the monkey has to travel at each time, using the step length parameter. For example, if the random integer generated is 0, then the 2D monkey travels along the x-axis with the step length increment; if 1 is produced the monkey travels in y-axis and for a value of 2 the monkey travels along both x,y axis. Similarly for the 3D monkeys, 0 for x-axis; 1 for y-axis; 2 for x-axis; 3 for x,y-axis; 4 for x,z-axis; 5 for y,z-axis; 6 for x,y,z-axis. Using the new traversal, the search space exploration by both the 2D and 3D monkeys were found to be improved, to cover the search space effectively. As both the newly introduced step size parameter and the xyz traversal help to cover the solution space in a better way, they were considered for further parameter tuning of the MA.

In the eighth test case, the tuned eye sight parameter with a value of 16.0 was used in combination with the newly introduced step size and the xyz traversal. Using these parameters resulted in better solution spread in the search space both for the 2D and 3D monkeys, suggesting better exploration and exploitation capabilities of the modified MA. Since, the test case 8 showed good solution search coverage capability, we decreased the step length from 0.001 to 0.0001 (test case 9) by retaining other parameters as that of test case 8. The solution space was better covered by the MA in the test case 9 than in 8, and the parameter used in this test case were taken as optimal for the design of new drugs.

Finally (test case 10), with the help of the dominance concept discussed earlier, the non-dominated solutions which are stored in the repository were used in the xyz traversal during watch-jump process to improve the quality of the solutions. The repository positions were used for 10% of the total population. In this case, the exploration and the exploitation capabilities of multiobjective monkey algorithm showed much improvement and for the given data set, the solutions obtained were as good as that of the solutions obtained with the multiobjective genetic algorithm [5].

• B.    Multi-objective Monkey algorithm for de novo drug design (MoMADrug)

The modified monkey algorithm discussed above with the tuned parameters was used for the de novo drug design problem. For this purpose, the MoMADrug was run 10 times each for two different reference molecules, Lidocaine and Furano-pyrimidine. The newly designed molecules obtained as optimal solutions from each run are shown in the Fig.3 and Fig.4 for the reference molecules Lidocaine and Furano pyramidine, respectively.

The fitness values of the designed molecules are listed in Table 3 and Table 4 for Lidocaine and Furano pyramidine, respectively. Some of the molecules were obtained as solutions more than once during the 10 runs. The molecules obtained were analyzed based on the objective functions – tanimoto similarity and OBA score. The best fit molecule obtained for Lidocaine has 0.57339 tanimoto similarity and OBA score of 1. In addition to this, other molecules with lower tanimoto similarity and OBA score of 1 were also obtained.

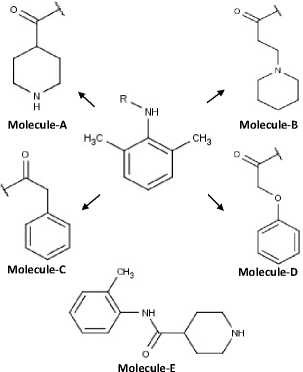
Fig.3. Optimal solutions of MoMADrug for Lidocaine

These results (designed molecules) are comparable to that of the results obtained using our previously developed genetic algorithm based de novo design tool MoGADdrug. The results of MoMADrug and MoGADdrug are compared in the Table 5 and Table 6 for reference molecules Lidocaine and Furano-pyramidine, respectively. MoGADdrug uses the same set of fragments to design molecules using genetic algorithm based multiobjective optimization. MoGADdrug also uses tanimoto similarity and OBA scores for evaluating the fitness of the designed molecules, but uses weighted sum of both the scores for final fitness calculation.

In the case of Furano-pyrimidine reference molecule, the MoMADrug designed molecule has a maximum tanimoto similarity of 0.54986 with an OBA score of 0.75. However, the best fit molecules (tanimoto similarity of 0.53583, 0.53386 with an OBA score of 1) designed using MoGADDrug were also obtained from MoMADrug, suggesting that MoMADrug can design more diverse set of molecules with varying levels of fitness value. More diverse solutions were obtained in MoMADrug than with MoGADdrug due to a tradeoff between the two objective values using the pareto-dominance method, which were not possible in the weighted sum approach used in MoGADdrug. In drug discovery multiple factors are involved in making a molecule as a successful drug and it is essential to start with diverse set of optimal molecules with diverse fitness to increase the chances of successful drug identification. The newly disclosed MoMADrug is able to design diverse set of molecules for drug discovery process.

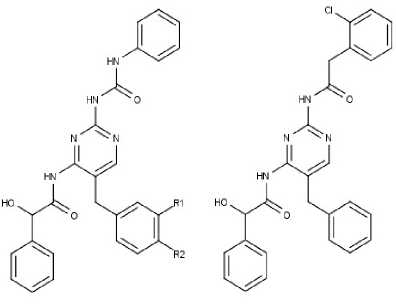
Molecule-F R1 = OCH , R2 = H       Molecule-I

Molecule-G R1 = H, R2 = OCH3

Molecule-H R1 = H , R2 = H

Molecule-J R1 = OCH , R2 = OCH

Fig.4. Optimal solutions of MoMADrug for Furano pyramidine

Table 3. MOMADRUG designed molecules (Mol.) for reference molecule - Lidocaine

Mol. (From 10 runs)	Fitness values
	Tanimoto similarity score	OBA score
A (5 times)	0.57339	1
B (1 time)	0.55022	1
C (2 times)	0.53738	1
D (1 time)	0.53247	1
E (1 time)	0.52863	1

Table 4. MoMADrug designed molecules (Mol.) for reference molecule – Furano pyramidine

Mol. (From 10 runs)	Fitness values
	Tanimoto similarity score	OBA score
F (6 times)	0.53583	1
G (3 times)	0.53386	1
H (1 time)	0.53312	1
I (1 time)	0.54986	0.75
J ( 5 times)	0.53704	0.75

Table 5. Designed molecules (Mol.) obtained from MoMADrug and MoGADdrug for Lidocaine

Mol.	MoMADrug		MoGADdrug
	Fitness values		Fitness value
	Tanimoto similarity score	OBA score
A	0.57339	1	1.5733
B	0.55022	1	-
C	0.53738	1	1.5374
D	0.53247	1	-
E	0.52863	1	1.5289

Table 6. Designed molecules (Mol.) obtained from MoMADrug and MoGADdrug for Furano pyramidine

Mol.	MoMADrug		MoGADdrug
	Fitness values		Fitness value
	Tanimoto similarity score	OBA score
F	0.53583	1	1.5358
G	0.53386	1	1.5338
H	0.53312	1	-
I	0.54986	0.75	-
J	0.53704	0.75	-

• VIII. Conclusion

To our knowledge, there is no report on the design and use of multi-objective monkey algorithm in the literature. This made us to propose a multi-objective monkey algorithm and apply it for de novo drug design. The proposed method along with its tuned parameters exploit and explore the 2D and 3D fragment library search space to arrive at better optimal solutions using pareto-dominance concept. The multi-objective monkey algorithm in comparison with genetic algorithm proves equally good in performance in arriving at the optimal drug-like molecules. As the traditional drug design and discovery is cost and effort consuming process, swarm intelligence algorithms such as multi-objective monkey algorithm can be helpful to discover drugs efficiently at lower cost in lesser time. In future, MoMADrug could be modified by incorporating new chemical reactions and also by increasing the size of the drug fragments library.