Multi Objective Optimization Model using Preemptive Goal Programming for Software Component Selection

Published Online August 2015 in MECS

MCDM or MOO problems are those where decisions are to be made over the set of available choices by having multiple usually conflicting attributes [6].The main aim of MCDM is to assist the decision maker in making the best choice by finding out the best alternative or by ranking the alternatives based on the choices. [7] Hence, the software component selection can be considered as the Multi-Criteria Decision Making Problem. In Multicriteria Optimization deals with simultaneously optimizing two or more conflicting objectives subject to certain constraints. When the criteria are different there are different methods to tackle with these problems like by using weighted sum method or by assigning priorities to the criteria. However, the weight coefficients in the former approach need to be determined explicitly which always depend on the subjective judgment of the developers. Whereas, it is easy to assign priorities on the objective by the developers.

There are different ways to solve these types of problems according to the conditions namely No preference method where the multiobjective optimization problem is solved using a simple method without consulting the decision maker. In Apriori methods the decision maker sets preferences before applying optimization. In case of Posteriori method representative sets of Pareto optimal solutions are presented to the decision maker so that s(he) can choose the best among them. As far as interactive methods are concerned it allows the decision maker to guide the search by alternating optimization and preference articulation iteratively. In case of Weighted sum method, a set of objectives are converted into single objective by premultiplying each user objective by user given weights. Similarly, €- constraint method takes one objective and keep the other objectives within the user specified values. Apart from these other methods are Weighted Metric Method, Benson Method, Value Function etc. Another important method is Goal Programming where instead of trying to optimize all the objectives we set goal for the objective values and try to meet these goals instead. Here, the objectives are assigned a specific value and a solution is found that minimizes the weighted sum of deviations of these objective functions from their respective goals. Depending upon types of goals there are two categories of goal programming “Pre-emptive Goal Programming” and “No- Preemptive Goal Programming”. In former, the priorities of the goals are in hierarchical order whereas in latter all the goals are of comparable importance. Goal Programming can be applied to different mathematical models like Linear programming, Non-Linear programming, Integer Programming, Zero-One Goal Programming etc .Our proposed model will make use of Zero- One preemptive Goal Programming as the software components are either selected or rejected.

This paper is organized into five sections. The related work in discussed in section 2, the next section 3 gives detailed discussion of proposed solution to multiobjective optimization model using preemptive goal programming. The section 4 gives an illustrative case study using LINDO taken from an online repository and section 5 is for results and discussions. The conclusion of the paper is given in section 6.

• II.    Related Work

So far, many researchers have proposed numerous approaches for software component selection as multiobjective optimization. Initially, the article by Vescan [8] proposes the component selection as multiobjective optimization with the problem of selecting components from the available set while minimizing the number of components selected and the cost of the components.

In the Multiobjective Optimization or Multicriteria decision making the earlier work done by [9] considers minimizing the number of used components, number of new requirements, number of provided interfaces and number of initial requirements that are not in the solution. It is solved using evolutionary algorithm which proceeds from the solutions found so far.

Another Multiobjective Optimization for software component selection under multi application development at a time was proposed in [10]. The objective is to minimize the total procurement cost and total adaptation cost of the selected components considering reusability and compatibility simultaneously. It is solved by using customary genetic algorithm which may not always give optimal result.

According to  [12] the objective function of the optimization model consists of software functionality and software quality like the reliability and user satisfaction. The user satisfaction is measured based on a set of factors. The model is solved using Binary particle swarm optimization.

Earlier some work was done for COTS Component Selection by using Goal Programming approach. As highlighted in [13] in order to choose components for a fault tolerant modular system such that the reliability of the system is increased while the overall price is reduced. Under this situation the use of chance constrained goal programming is suggested as it minimizes the nonconformity between the attainment level of the objectives and the goals set for them.

Another work by [14] considers the selection problem of repairable component for parallel series system as a multiobjective optimization problem. Two models are proposed and solved using preemptive goal programming. The solution improves the reliability of the selected system with compromised solution of repairable changes.

After studying the previous work it was noticed that all the techniques were considering cost to be reduced while taking care of different factors like non functional requirements, compatibility, buy versus build decision etc. But in case components are retrieved from online repository as a result of keyword search, it is difficult to retrieve the best suited component according to the given parameters like Bestseller based rating, Review based rating, download based rating etc. For these types of scenarios the authors propose a new multiobjective optimization model that is solved using preemptive goal programming.

• III.    Proposed Solution To Multiobjective Optimization Model Using Preemptive Goal Programming

In Multi objective optimization the goal programming method is one of the oldest technique which works on the principle of minimizing the deviation of each of the objective from the desired level. An important review was done by Orumie in [15] and comparison of different algorithms was made on the basis of computational time and accuracy. However, in the software component selection technique the application developer needs to select the desired component from the repository based on his/her requirements and the goal programming method has been rightly adapted.

The Preemptive Goal Programming is considered for solving this optimization problem as the idea behind this is that lower priority goals should not be achieved at the cost of higher priority goals, they are preempted. In the Goal Programming method the objectives are converted into goals and for each goal a pair of deviation variables are defined. Mathematically, it is represented as:

Gi : fi(x) + Ui - Ei for i=1,2,3….N where N is the number of Goals fi(x) is the mathematical expression for the goal

U i & E i are the deviational variables for each goal.

U i the amount by which the left side falls short of (under) its right hand side value

E i is the amount by which the left side exceeds its right hand side value.

After formulating the goals the next target of Goal Programming is to minimize the Detrimental variables. There are three different cases as highlighted in [16] :

• i) . If f i (x) >= B i , Goal is attached to maximization type of objective. Here, the decision maker does not want under achievement with respect to target B i . Hence, U i is to be minimized.

• ii) . ii) If f i (x) =< B i , Goal is attached to minimization type of objective. Here, the decision maker does

not want over achievement with respect to target B i . Hence, E i is to be minimized.

• iii) . If f i (x) = B i , Goal is to be achieved exactly. Here, the decision maker neither wants under achievement nor over achievement with respect to target B_i. Hence, (U_i + E_i) is to be minimized as both are equally unwanted.

This model is applicable to any situation where the developer has clear idea in his/her mind about the requirements, constraints and the priorities of these requirements. In terms of goal programming, the hard constraints, goal constraints and the priorities need to be defined. The number of hard constraints and goal constraints can be more than one. Even the priorities can range from two to some greater number. In the present case, the hard constraints are the budget and the number of components to be retrieved. The goal constraint according to the priorities are bestseller rating is at the first priority, secondly download rating and thirdly review based rating is considered. Moreover, the component is either selected or rejected so Zero-One goal programming is used.

The general Zero-One Goal Programming model in selecting the optimal set of components can be stated as follows:

Minimize Z = P i (w n p 1 , w m p 2 , w o p 3 )        (1)

Subject to

Hard Constraints

L j⁰1 Pj Cj < = Budget Max_allocated           (2)

That means the total budget of the selected components should be within the budget limitations

X j° ₁ Cj = No._of_Components_to_be_selected (3)

Goal Constraints

Ь[С[ + bjC- + nj — Pj < sum_of_top_bestseller_rating(4)

djCj + djCj + nj — Pj < sum_of_top_downloaded_rating(5)

TjCj + TjC- + nj — Pj < sum_of_top_reviewbased_rating(6)

Cj- = 0 or1(7)

CjnjPj > 0

where

Pi = Sum i preemptive priority(P1 > P2 > P3) for i= 1,2,3…n wn = The weightage assigned to the 20 components nj,pj = The negative and the positive deviation variables are for i =1,2….n components.

P j = Coefficient of components in term of price associated.

b j = Coefficient of components in term of best seller rating associated.

d j = Coefficient of components in term of download rating associated.

T j = Coefficient of components in term of review based rating associated.

Now this model can be implemented in popular optimization software package LINDO. The Implementation is shown in the next section.

• IV.    An Illustrative Example Using Lindo

Consider a hypothetical problem where the developer is looking for the .Net components for managing the documents in an organization. The requirements can be stated as below:

• i.    The user is able to annotate the document by adding the comments, highlighting some text, images, tables etc.

• ii.    The user is able to merge the documents and can easily identify the difference between two versions of the same document.

• iii.    The user is able to retrieve information across the websites.

The developer will look for components satisfying these requirements. S(he) considers the free online repository for the components. The developers realizes that a vast set of components are available corresponding to the requirements on this website, s(he) is actually puzzled that which components to be selected based on the information that is provided on the site. By following the classification provided based on the requirements, the developer reaches at a point where a set of twenty components are available based on the stated requirements. Each component is provided with the following information:

• 1.    Textual description of the functionality provided by the component.

• 2.    The pricing of the components, like the individual cost or the cost of more than one licensed version of the component.

• 3.    The components are rated based on the past purchases under the bestseller rating.

• 4.    Each time a developer buys a component s(he) writes a review on it, based on the reviews also the components are rated.

• 5.    The number of times the trial version  are

• 6.    The asset value which denotes the time and experience required if the component is developed inhouse.

downloaded, this parameter is also taken into consideration when the components are ranked or rated.

The developer wants to select the component set which is optimal using all these criteria so based on his intuition/judgment/experience considers the component to be selected, in the following priority levels, by fixing the cost for the components and the number of components to be retrieved:

• 1.    The selected component should be in the top five bestseller component.

• 2.    The chosen component should be in the top ten components in the download based rating.

• 3.    In the review based rating the chosen component should be among the top ten components.

This software component selection problem is a good candidate for solving with Goal Programming as goals are set for the objective values and he tries to achieve all these goals.

• A.    Decision Variable

• B.    Hard Constraints

AccoTding to the model the hard constraints are on the budget and number of components, as depicted below:

157500c 1 + 157500c 2 + 113400c₃ + 157500 c₄ + 157500 c₅ + 2400 c₆ + 6300 c₇ + 4700 c₈ + 31400 c₉ + 44000 c₁₀ + 94400 c 11 + 62900 c₁₂ + 201600 c₁₃ + 56600c₁₄ + 50300c₁₅ + 34600c₁₆ + 18800c₁₇ + 50300c₁₈ + 12500c₁₉ + 40900c 20 < 200000

X -.O                    (9)

• C.    Goal Constraints

There are three goal constraints, that are considered according to the priorities named as priority 1, priority 2 and priority 3 goals. Each priority corresponds to bestseller rating, download rating and review based rating.

Table 1 .Net components for document management

Component	Pricing	Bestseller Rating	Review Rating	Dow nload Ratin g
C1GroupDocs.Comparison	157,500	1	2	6
C2GroupDocs.Assembly	157,500	2	3	13
C3Vizit	113400	5	5	2
C4GroupDocs.Annotation	157,500	3	4	5
C5GroupDocs.Viewer	157,500	4	1	9
C6Covri   Parent   Selector Column Web Part	2400	6	6	17
C7Covri Cascaded Lookup Web Part	6300	8	8	8
C8Covri CrossSite Lookup Web Part	4700	7	7	18
C9Virto Active Directory User Service for SharePoint	31400	11	11	10
C10,Virto Create & Clone AD User Web Part	44000	10	10	14
C11,   Virto   Workflow Activities Kit	94400	9	9	15
C12, jungle doc	62900	17	17	7
C13,KWizCom  SharePoint Wiki Plus	201600	12	12	16
C14    SharePoint    AD Information Sync	56600	13	13	11
C15,SharePoint Batch Check In	50300	18	18	4
C16,SharePoint  Document Auto Title	34600	19	19	20
C17 SharePoint Document Number Generator	18800	15	15	3
C18,SharePoint Document Viewer	50300	16	16	1
C19 SharePoint Item Audit Log	12500	14	14	19
C20 SharePoint RichText Boost	40900	20	20	12

• •    Priority 1

The software component to be selected should be among the top 5 bestseller components. Here the developer doesn’t want overachievement with respect to the target.

1с 1 + 2с 2 + 5с 3 + 3с₄ +4с₅ + 6с₆ + 8с 7 + 7с 8 + 11 с₉ + 10с_1о+ 9с 11 + 17с₁₂ + 12с₁₃ + 13с₁₄ + 18с 15 + 19с₁₆ + 15 с 17 + 16с 18 + 14с 19 + 20с 2о + У 1 -У 2 < 15

• •    Priority 2

From the repository of 20 components the components to be selected should be among the top 10 of the number of download based rating.

6с 1 + 13с₂ + 2с₃ + 5с₄ + 9 с₅ + 17 с₆ + 8 с₇ + 18 с₈ + 10с₉ + 14с₁₀ + 15с 11 + 7 с₁₂ + 16с₁₃ + 11с₁₄ + 4с 15 + 20с 1б + 3с 17 + Тс хд + 19с 19 + 12с 2о + У з - У 4 < 55

• •    Priority 3

2с 1 + 3с₂ + 5с₃ + 4с₄ +1с₅ + 6с 6 + 8 с₇ + 7с 8 + 11с₉ + 10с₁₀+ 9с 11 + 17с₁₂ + 12с₁₃ + 13с₁₄ + 18с 15 + 19с₁₆ + 15 с 17 + 16с 18 + 14с 19 + 20с 2о + У₅ - У б < 55

• D.    Objective Function

The Goal Programming is to minimize the value of the objective function subject to goal constraint and satisfying the pre-emptive priority goals.

Minimize (у2 + у4 + у6)          (13)

The above mentioned constraints and objective functions when executed on LINDO gives results as discussed in the subsequent section.

• V.    Results And Discussion

In the software component selection problem either the component is selected or rejected so we are considering Zero-One Goal programming [17].

At the first run, y2 is minimized and if the objective function value is zero that means the first priority is fully satisfied. As shown in the figure 1, all the target values are achieved. The reduced cost column shows that amount by which the objective coefficient of the variable would have to improve before it would become profitable to bring that variable into the solution at a nonzero value. There is a slack in the three goal constraints, which is tolerable according to our priorities. The initial set of components retrieved includes c1, c6 and c8.According to priority 1 goal constraint the sum of prices of three components is Rs 1,64,600 with a slack of Rs 35400 as shown in fig. 1.Similarly, for the download based rating the rating for the selected components is 6,17 and 18 respectively and the sum has a slack of 14 as shown in the fig.1.

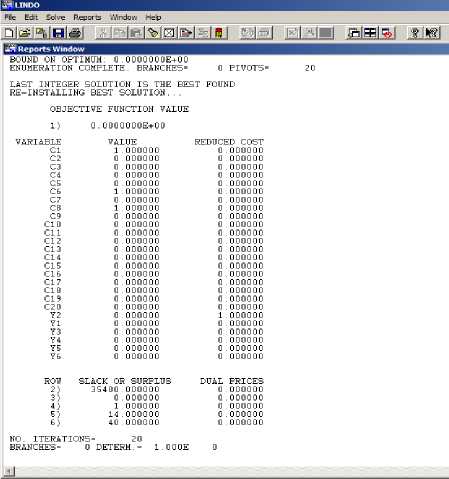
Fig. 1. The report window for minimizing y 2

In the second run, for minimizing y4, the value of y2 is added as to the set of constraints. On solving the model the results obtained are shown in fig. 2. That shows similar results to fig. 1 but the constraint y4 has been minimized to zero.

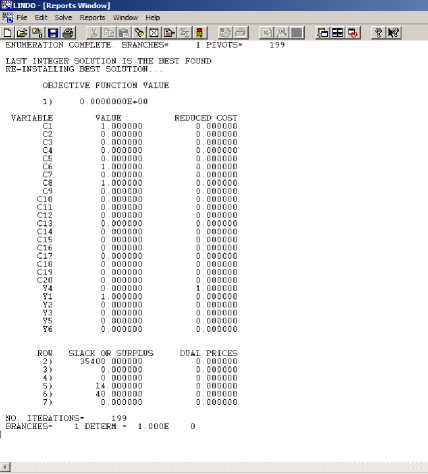
Fig. 2. The report window for minimizing y4

Subsequently, in the third and the final run the value of y2 and y4 are added to the set of constraints while minimizing y6. It is depicted in fig. 3 that there is a slack in achievement of goal constraints but the hard constraints are fully met.

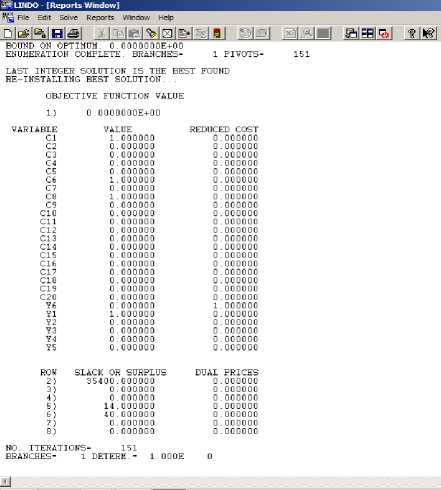
Fig. 3. The report window for minimizing y6

There is a zero slack for the bestseller based rating and 40 for the review based rating, The final component set is c1 (GroupDocs.Comparison), c6 (Covri Parent Selector Column Web Part) and c8 (Covri CrossSite Lookup Web

Part).The retrieved components are according to the functionality desired like the component can easily make out the differences in the revised version of the document and it will be able to hierarchically the information across various websites.

• VI.    Conclusions

The Component Based Software Development is the latest paradigm to achieve the reusability that results in low development cost and accelerated delivery. The software component selection is done based on the functionality. The component repository also provides some meta data to make the decision of selecting the best fit component. The proposed model attempts to find the best candidate components based on the user set priorities from an online repository. After mathematically formulating the problem, it provides interesting results based on the given goals and user preferences. All the rigid conditions are specified explicitly and the user defined priorities are also taken into consideration based on this the optimal component sets are generated. This approach gives satisfactory results when the component repository is small and the number of components to be retrieved are also less. But for larger repository this may not give optimal results in that case fuzzy clustering will be used which will be considered in the future work.