Multi-objective Structural Optimization Using Fuzzy and Intuitionistic Fuzzy Optimization Technique

Published Online April 2015 in MECS

Structural optimization is an important concept in structural and civil engineering. Although structural optimization is a traditionally well known concept, in many instances it is treated in single objective form, where the objective is known to be ‘the weight function’. As an extension of this is the optimization where one or more constraints are simultaneously satisfied next to the minimization of the weight function. This does not hold in real world problems where multiple and conflicting objectives frequently exist. The accomplishment of this task is due to the methodology known as multi-objective structural optimization (MOSO). The MOSO is gaining gravity especially in the last decade due to the increasing technological demand of structural optimization.

In structural engineering design problems, the input data and parameters are often fuzzy/imprecise with nonlinear characteristics that necessitated the developments of fuzzy optimum structural design method. Fuzzy set (FS) theory has long been introduced to handle inexact and imprecise data by Zadeh [2]. Later on

Bellman and Zadeh [3] used the fuzzy set theory to the decision making problem. The fuzzy set theory also found application in Structural Model. Several researchers like Wang et al. [1], Rao [8] ,Yeh et.al [7], Xu [6], Shih et.al [9-11], Dey et. al [5] ,Huang et.al [18] made distinctive implementation of the fuzzy set theory.

In view of growing use of fuzzy set in structural problems under situations when information available is imprecise various extension of fuzzy sets immerged. In such extension, Atanassov [12,14,16] introduced Intuitionistic fuzzy set (IFS), is one of the generalizations of fuzzy set theory, is characterized by a membership function, a non membership function and a hesitancy function. IFS is very suitable for the depiction of the uncertainty and vagueness of things. The concept of IFS can be viewed as an alternative approach to define a fuzzy set in a situation where available information is not sufficient for the definition of an imprecise concept by means of a conventional fuzzy set. In fuzzy sets the degree of acceptance is only considered but IFS is characterized by a membership function and a nonmembership function so that the sum of both values is less than one. The concept of membership and nonmembership was considered by Angelov[13,15] in optimization problem and gave intuitionistic fuzzy approach to solve optimization problems. Now intuitionistic fuzzy optimization (IFO) is an open field for research work. Very little research work has been carried out on IFO in application to structural optimization. Luo.et.al [21] applied the inclusion degree of intuitionistic fuzzy set to multi criteria decision making problem. Pramanik and Roy [17] solved a vector optimization problem using an intuitionistic fuzzy goal programming. A transportation model was solved by Jana and Roy [19] using multi-objective intuitionistic fuzzy linear programming. Dey et. al [20] use Intuitionistic fuzzy optimization technique to optimize non-linear single objective two bar truss structural model.

In this paper, a well known three bar truss [22] design model is considered as a Structural design model. The results are compared numerically both in fuzzy optimization technique and intuitionistic fuzzy optimization technique. From our numerical result, it is clear that intuitionistic fuzzy optimization provides better results than fuzzy optimization.

The advantage of the intuitionistic fuzzy optimization technique is twofold: they give the richest apparatus for formulation of optimization problems and on the other hand, the solutions of intuitionistic fuzzy optimizations can satisfy the objective(s) with bigger degree than the analogous fuzzy optimization problem and the crisp one. This paper envisages the application of IFO in context of structural design.

The remainder of this paper is organized in the following way. In section II, we discuss about Multiobjective Structural Model. In section III, we discuss about fuzzy set, intuitionistic fuzzy set, a -cut and ( a , в ) -cuts. In section IV, we discuss Solution of Multiobjective Nonlinear Programming Problem by fuzzy and intuitionistic Fuzzy Non-Linear Programming technique with linear membership and non-membership functions. In section V, we discuss about Solution of Multiobjective structural optimization Problem by fuzzy and intuitionistic fuzzy optimization technique. In section VI, we discuss about numerical solution of structural model of three bar truss and compared results by Intuitionistic Fuzzy Non-linear programming (IFNLP) technique and by fuzzy non-linear programming (FNLP) technique. Finally we draw conclusions from the results in section VII.

• II.    M ulti - objective S tructutal M odel

In the design of optimal structure i.e. lightest weight of the structure and minimum deflection of loaded joint that satisfies all stress constraints in members of the structure. In truss structure system, the basic parameters (including the elastic modulus, material density, the maximum allowable stress, etc.) are known and the optimization’s target is that identify the optimal bar truss cross-section area so that the structure is of the smallest total weight, the minimum nodes displacement, in a given load conditions.

The multi-objective Structural model can be expressed as

Minimize WT ( A )

minimize 3 ( A )

subject to        ст ( A ) <  [ ст ]

Amin < A < A max where A = [ Ax, A,....., A ]Г are design variables for the cross section, n is the group number of design variables

E n

PAL is the total weight of the structure, 3 (A) is the deflection of loaded joint, where Li, Ai and pi are the bar length, cross section area, and density of the ith group bars respectively. ст(A) is the stress constraint and [ст] is allowable stress of the group bars under various conditions, Amin and Amax are the lower and upper bounds of cross section area A respectively.

• III.    P rerequisite M athematics

• A.    Fuzzy Set

Let X denotes a universal set. Then the fuzzy subset A in X is a set of order pairs A = { x e X : ( x , p ( x ) ) } where p : X ^ [0,1] is called the membership function which assigns a real number p ( x ) in the interval [0, 1], to each element x e X . A is non fuzzy and p ( x ) is identical to the characteristic function of crisp set. It is clear that the range of membership function is a subset of the non-negative real numbers.

• B.    a -Level Set or a -cut of a Fuzzy Set

The a -level set of the fuzzy set A of X is a crisp set A _a that contains all the elements of X that have membership values greater than or equal to a i.e. A = { x : p ( x ) >  a , x e X , a e [0,1] } .

• C.    Intuitionistic Fuzzy Set

Let X = { x 1 , x 2 ,..., x_n } be a finite universal set. An Intuitionistic fuzzy set (IFS) Aⁱ in the sense of Atanassov’s [..] is given by equation

Ai=Kx, pi(xi ),uf(xi))/xie X} where the functions and

U i ( x i ): X ^ [0,1]; x i e X ^ и^ ( x i ) e [0,1]

define the degree of membership and the degree of non-membership of an element x i e X to the set A с X , respectively, such that they satisfy the condition 0 <  p, ( x i ) + и i ( x i ) <  1 , V x i e X . For each IFS A in X, the amount n^* ( x i ) = 1 — ( p i ( x i ) + U i ( x i )) is called the degree of uncertainty (or hesitation ) associated with the membership of elements x i e X in A .We call it intuitionistic fuzzy index of A with respect of element ^x i ^{e X} .

• D.    ( a , в ) -level intervals or ( a , в ) -cuts

A set of ( а , в) - cut , generated by an IFS A where а , в g [ 0,1 ] are fixed numbers such that а + в <  1 is defined as

i

A a, в

(x , и i ( x ), и i ( x ) ) / x G X ,

AA

U i ( x ) ^ a , и i ( x ) <  в , а , в g [ 0,1 ]

We define ( а , в ) - level or ( а , в ) - cut, denoted by

А а , в , as the crisp set of elements x which belong to A at least to the degree а and which belong to A at most to the degree в .

L = min { ф ( x p ) } where

L = Ф i * ( x i ) ,1 <  i <  P .

1 <  i <  p . It is obvious

Step 4: Using aspiration level of each objective of the MONLP of (2) may be written as follows.

Find x so as to satisfy

Ф , -( x ) < L i  ( i = 1,2,3,....., p )

V j ( x ) < ^b j , j = 1,2,..., m                             (3)

x >  0,

Here objective functions of (2) are consider as fuzzy constraints. These types of fuzzy constraints can be quantified by eliciting a corresponding membership function и (ф ( x ) ) , i = 1,2,3,....., p

• IV.    M athematical A nalysis

  if Ф ( x ) <  L i

  
  

• A.    Fuzzy Non-Linear Programming (FNLP) Technique to Solve Multi-objective Nonlinear Programming Problem (MONLP)

A multi-objective non-linear programming (MONLP) problem may be taken in the following form:

Minimize {ф (x),....., ^ (x)} subject to      V (x)< b., j = 1,2,...,m            (2)

x >  0,

Following Zimmermann [4], we have presented a solution algorithm to solve the MONLP problem by fuzzy optimization technique

Step 1: Solve the MONLP (2) as a single objective non-linear problem p times for each problem by taking one of the objective at a time and ignoring the others. These solutions are known as ideal solutions. Let xⁱ be the respective optimal solution for the i^th different objective with same constraints and evaluate each objective values for all these i^th optimal solution.

Step 2: From the result of step 1, determine the corresponding values for every objective for each derived solution. With the values of all objectives at each ideal solution, pay off matrix can be formulated as follows

Ф 1 ( x ) Ф 2 ( x )  " •    Ф р ( x )

x¹   Ф 1* ( x )    Ф ^Г ( ^{x 1} )   “   Ф р ( ^{x 1} )

x²   Ф *( x ² )    Ф ^г ( x ² )  •     Ф р ( x ² )

x p   ф Г( x^p )   Фг( x p )  •     Ф 2* ( x^p )

Here x1,x2,....,xp are the ideal solutions of the objectives ф (x),.....,ф (x) respectively.

Step 3: From the result of Step 2, now we find lower bound (minimum) L and upper bound (maximum) U by using following rule    U_t = max { ф ( x p ) }    ,

М 1 ( ф .^{( x} ) ) = •

U i - Ф i ( x ) •  U i ^- L .

if L < ф ,⁽ x ) <  U i

if Ф 1 (^x ) ^ Ui

Rough sketch of the membership function for objective functions is shown in figure 1.

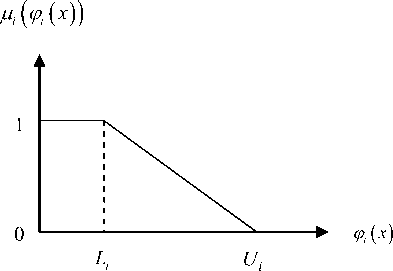
Fig. 1. Rough sketch of membership function for objective function

Under the concept of min-operator, the feasible solution set is defined by interaction of the fuzzy objective set .This feasible solution set is then characterized by its membership и (x) which is:

U D ( ^x ) = min ( U 1 ( Ф 1^{( x} ) ) , U 2 ( Ф 2^{( x} ) ) ,.... ^, U p ( Ф р ^{( x} ) ) ) ⁽⁵⁾

The decision solution can be obtained by solving the problem of maximize и ( x ) subject to the given constraints i.e.

Maximize minimize и ( x )

V x > 0     \     V i          i/ such that  Vj (x)< b.,(6)

x >  0, j = 1,2,..., m ; i = 1,2,3,...., p .

Now if suppose а = minimize и (x) be the overall V ii satisfactory level of compromise, then we obtain the following equivalent model

Maximize а such that m(x) > а, i = 1,2,3,....,p.

V ( x ) <  bj = 1,2,..., m. x >  0, а e [ 0,1 ]

Step 5: Solve (7) to get optimal solution.

• B.    An Intuitionistic Fuzzy Approach for Solving Multiobjective Nonlinear Programming Problem with Linear Membership and Non-Membership Functions Following Zimmermann[4] and Angelov [15], we have presented a solution algorithm to solve the MONLP (2) by Intuitionistic Fuzzy Optimization (IFO) technique.

Here Step 1 and Step 2 are same as shown in IV-A.

Step 3: From the result of Step 2, now we find lower bound (minimum) LAcc and upper bound (maximum) UA™ by using following rule UA" = max {ф (xp)} , LAc = min {ф (xp)} where 1 < i < p . But in IFO the degree of non-membership (rejection) and the degree of membership (acceptance) are considered so that the sum of both values is less than one. To define the nonmembership function of NLP problem, let URej and LRej be the upper bound and lower bound of the objective functions ф (x)  where LAcc < LRe < UR < UAcc . For objective function of minimization problem, the upper bound for non-membership function (rejection) is always equals to that the upper bound of membership function (acceptance). One can take lower bound for the nonmembership function as follows  LR = LAcc + ^  , where 0 < ^ < (UAcc - LAcc), based on the decision maker choice.

The initial intuitionistic fuzzy model with aspiration levels of objectives becomes

Find

So as to satisfy

ф(x)<‘AR0 with tolerance PAc = (UiAcc - LAcc) for the degree of acceptance for i = 1,2,...., p фг( x )> iURej with tolerance PR =( UR - LRe) for the degree of rejection for i = 1,2,...., p

Define the membership (acceptance) and nonmembership (rejection) functions of above uncertain objectives as follows

For the i^h , i = 1,2,...., p objectives functions the linear membership function M ( ф ( x ) ) and linear nonmembership ц ( ф ( x ) ) is defined as follows:

	1	if ф . ( x ) <  L A cc
M i ( ф ( x ) ) = '	UAcc - ф ( x ) UA:c - L A cc	ifL Acc <  ф ( x ) <  U A"C
	11	if ф ( x ) >  U A c
	I 0	if ф ( x ) < L R
U i ( ф ( x ) ) =	ф ( x ) - L Re U Re - L Re	гfL R ej <  ф ( x ) <  U R j
	1	if ф( x ) > U R

Rough sketch of the membership function and nonmembership function for objective functions is shown in figure 2.

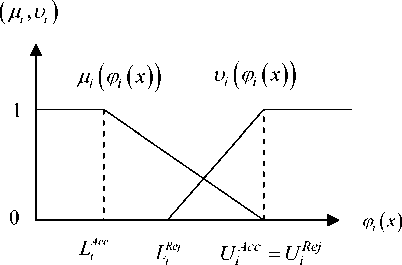
Fig. 2. Rough sketch of membership and non-membership function for objective function

Step 4: Now an intuitionistic fuzzy optimization for above problem with membership and non-membership function can be written as

Maximize V i

( M i (ф, ^{( x} ) ) )

minimize

V i

( ^ц г ⁽ ф ^{( x} ) ) ) ,

subject to

Mi (ф (x)) > U (ф (x)), i = 1,2,....p; j = 1,2,......,m

Find an equivalent crisp model by using membership and non-membership functions of objectives by IF as follows:

Max ( min ( m , M ,

...

., m ) ) — Min ( max ( ц , U

subject to

A i ( Vi ( x ) ) + ^U i ( v i ( x ) ) < 1,

Ai (vi (x)) > Ui (vi (x)),

U i ( V i ( x ) ) >  0,

V j ( x ) <  0,                                ⁽⁹⁾

x >  0;

i = 1,2,.... p ; j = 1,2,, m

If we consider a = minimize ( a , a ,..., a ) and в = maximize ( ц , u >- U ,) , according to Angelov [15] ,the above can be written as:

Maximize ( a - в )                            (10)

subject to A i ( v i ( x ) ) >  a ,    U i ⁽V i ^{( x} ) ) <  ^{в ;}

Vj (x) < 0, x > 0; a + в < 1, a e[0,1],в e [0,1];i = 1,2,....p; j = 1,2,......,m which on substitution for Ai (vi (x))  , Ui (vi (x))

for i = 1,2,.... p . (10)

becomes

Maximize ( a - в )

subject to vi (x) + a (l'A - P") < U Ac vi (x)- в (-  R   lR )< lR          (11)

V j ( x ) < 0

a + в <  1, a e [0,1], в e [0,1];

i = 1,2,.... p ;   j = 1,2,......, m

Step 5: Solve the above crisp model (11) by using appropriate mathematical programming algorithm to get optimal solution of objective function.

Step 6: Stop.

• V.    S olution O f M ulti - objective S tructural O ptimization P roblem B y F uzzy A nd I ntuitionistic F uzzy O ptimization T echnique

To solve the MOSOP (1), step 1 of IV-A is used. After that according to step 2 pay-off matrix is formulated as follows:

After that according to step 2, the bounds of objective are    U^Acc , L^Acc   for weight function    WT ( A )

(where    L A^CC <  WT ( A ) <  U Acc   )    and L R , U R

(where L R ^e <  WT ( A ) <  U R ,), IU , L A for deflection function   5 ( A )   (where   L A ^cc <  5 (A ) <  UR  ) and

LR , UR      where      LR < 5( A) < UR     , where UA = UR ;1R = L + e,  for i = 1,2. such that 0 < e < ( UAc - LAcc) are identified.

According to IFO technique, considering membership and non-membership function for MOSOP (1) crisp nonlinear programming problem is formulated as follows

Max(min ( Awt (WT (A)), A5 (5 (A)))) - min(max(u^ (WT(A)),ц (5(A))))

subject to

A wt ( WT ( A ) ) + U wt ( WT ( A ) ) < 1,

A 5 ( 5 ( A ) ) + Ц 5 ( 5 ( A ) ) < 1,

A wt ( WT ( A ) ) > U wt ( WT ( A ) ) ,

A 5 ( ⁵ ( ^A ) ) > ^U 5 ( ⁵ ( ^A ) ) ,

U wt ( WT ( A ) ) > 0, U 5 ( 5 ( A ) ) > 0, ct ( A ) <  [ ст ]; A >  0

According to Angelov [15], the above problem can be written as

Maximize ( a - в )                           (13)

subject to

A wt ( WT ( A ) ) > a , U wt ( WT ( A ) ) < в ;

A 5 ( ⁵ ( ^A ) ) > ^a , ^U 5 ( ⁵ ( ^A ) ) < ^в ;

ст ( A ) <  [ ст ], a + в <  1, A >  0, a g [0,1], в e [0,1];

Solve the above crisp model (13) by an appropriate mathematical programming algorithm to get optimal solution and hence objective function i.e. structural weight and deflection of loaded joint will get the Pareto optimal solution.

• VI.    N umerical S olution O f a M ulti - objective S tructural O ptimization M odel of a T hree B ar T russ

A well-known three bar [22] planar truss structure is considered. The design objective is to minimize weight of the structural WT ( A , A ) and minimize the deflection 5 ( A 1 , A 2 ) along x and y axes at loading point of a statistically loaded three-bar planar truss subjected to stress ( ст ) constraints on each of the truss members.

WT ( A )     5 ( A )

Ai WT*( A1)  5 (A1)"

A ² WT ( A ² )   5 *( A ² )

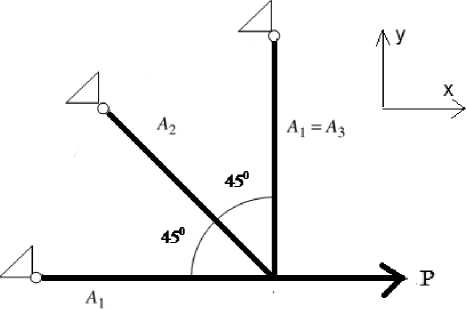
Fig. 3. Design of the three-bar planar truss

A ¹

A ²

A ³

WT ( A 1 , A 2 ) 2.187673 15 10.1

S , ( A 1 , A 2 )      S y ( A ! , A 2 )

20     5.857864

3             1

3.960784  0.039216

Here

Wac = 15 = Wjf , Wacc = 2.187673 , Wre = W"' + 6 , where 0 < 61 <(15 - 2.187673)  ; S acc = 20 = S и , acc             rej        acc

SxL = 3, Sx L = Sx L + 62, where

0 <  62 < ( 20 - 3 )     ; S и = 5.857864 = S rej

S™ = 0.039216, S y7 = S y^ + 6 3 ,

The multi-objective optimization problem can be stated as follows:

Minimize WT ( A 1 , A 2 ) = p L ( 2 A 1 + A 2 )

minimize S x ( A 1 , A ₂ ) =

minimize S _y ( A 1 , A ₂ ) =

PL ( 2 A + A ) E ( 2 A ² + 2 AA )

PLA

E ( 2 A ² + 2 AA )

where 0 <  6 3 < ( 5.857864 - 0.039216 ) ; Here linear membership and non-membership function for the objective functions WT ( A 1 , A ₂) , S ( A , A ₂ ) and S ( A , A ) are defined as follows:

M wt (WT (Д, A 2 ))

1              ifWT ( A 1 , A ₂) — 2.187673

= <

subject to 7 1 ( A 1 , A ₂ ) -

⁷ 2 ⁽ A 1 , A 2 ) -

⁷ 3 ⁽ A 1 , A 2 ) ^-

min

P ( 2 A 1 + A 2 )     „ T

2 A_XA₂ + 2 A 2 ^ ^0-1

P T

— I 7 n

• V2 (A + A2) L

PA

• ²---2 — ¹ 7

2 AA + 2 A ^{2   L}

< A i — A i max ; i = 1,2

Where P = applied load; p =material density, L =Length, E=Young’s modulus, A1 = cross section of bar-1 and bar-3 A =cross section of bar-2. S and S, are xy the deflection of loaded joint along x and y axes respectively. |7T J and ^7T J the maximum allowable tensile stress for bar 1 and bar 2 respectively. ЦтТ J is the maximum allowable compressive stress for bar 3.

¹⁵   WT ⁽ A 1 , A ₂) if 2.187673 — wt ( a , A ) — 15

12.812327                 12

0              ifWT ( A 1 , A ₂) >  15

U wt (WT ( A„ A 2 ))

0                        if WT ( A , A ) — 2.187673 + 6

= - ^{WT (} A ¹ , A ² ) ^{- (2.638958 + 6} 1 ) if 2.187673 + 6 — WT ( A ,, A ₂) — 15

12.812327 - 6                       ¹         1 ,

_ 1                              if WT ( A , , A 2 ) > 15

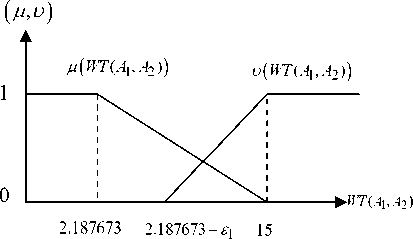
Fig. 4. membership and non-membership function for WT ( A ₁, A ₂)

The input data for MOSOP (14) is given as Applied load (P) = 20KN; Volume density ( p ) =100 KN / m ³; Length (L) = 1 m; Maximum allowable tensile stress T TY J = 20 KN / m ² ;Maximum allowable tensile stress TT J = 10 KN / m ² ;Maximum allowable compressive stress | a C ' J =20 KN / m ² ;Young’s modulus (E)=2 x 10⁷ KN / m ² and 0.1 x 10 - 4 — A , A — 5 x 10 - 4 mm

Solution: According to step 2 pay off matrix is formulated as follows:

Ms, ( S x ( A 1 , A 2 ))

'1                 if S x ( A 1 , A 2 ) — 3

= _<  ^{20 - S} x ⁽ A 1 , A 2 ) if. 3 — s ( a , a₂ ) <  20

17                  x V 27

_ 0                if S x ( A 1 , A 2 ) >  20

U s ( S x ( A 1 , A 2 ))

0                   if S , ( A_v A 2 ) — 3 + 6 2

= >  ^S x ( A ¹’ A 2 ) ^{- (}3 + ⁶ 2 ) if 3 + 6 2 — S , ( A 1 , A 2 ) — 20

^{17 - 6} 2

_ 1                      if S , ( A 1 , A 2 ) >  20

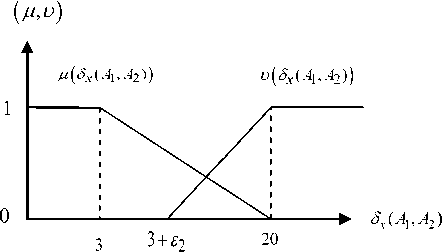
Fig. 5. membership and non-membership function for S _x ( A , A ₂)

20 ( 2 A + A ₂) 2 A ² + 2 AA

20 A

2 A ² + 2 AA

+ 17 а <  20;

+ 5.818648 а <  5.857864;

²⁰ (² A 1 + ^A 2 ) _<20. 2 A ² + 2 AA    ’

_r ²⁰    <  10;

V2 ( A 1 + A ₂ )

20 A

, ^{( 2} )   <  20;

2 A ² + 2 AA

0.1 <  A 1 , A ₂ <  5, а e [ 0,1 ] ,

^s, ( S y ( A 1 , A 2 ))

'1                      f S ( A 1 , A ₂) <  0.039216

5.857864 - S y ( A 1 , A ₂)

5.818648

1f 0.039216 <  S y ( A 1 , A ₂) <  5.857864

0                    f S y ( A 1 , A ₂) >  5.857864

U, ( S y ( A 1 , A 2 )) ' 0

Now using IFO technique with membership and nonmembership functions we get,

Maximize (а - в)

subject to

( 2 A + A ) + 12.812327 а <  15;

( 2 A + A ) - (1 - в )(2.187673 + £ ) <  15 в ;

if S y ( A 1 ,A ₂) < 0.039216 + £ ₃

20 ( 2 A + A )

S, (A, A,) - 0.039216 - £ y 1  2-------------3if 0.039216 + e3

5.818648 - £                 ³ y ¹²

if S y ( A 1 , A ₂) >  5.857864

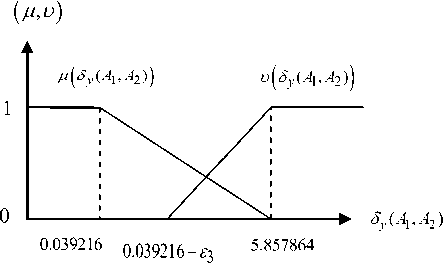
Fig. 6. membership and non-membership function for ^ ( A ], A ₂ )

2 A ² + 2 AA 20 ( 2 A + A ) 2 A ² + 2 AA

20 A 2

2 A ² + 2 A A

+ 17 а <  20;

- ( 1 - в ) (3 + £ 2 ) <  20 в ;

+ 5.818648 а <  5.857864;

20 1.

—₂---²-- (1 - в )(0.039216 + £ ) <  5.857864 в ;

2 A ² + 2 AA

20 ( 2 A + A )

2 A ²

+ 2 AA

< 20;

Now using Fuzzy optimization technique we get,

Maximize а subject to

( 2 A + A ) + 12.812327 а <  15;

2 ^{0 (} A 2 )    <  20;

2 A ² + 2 AA

0.1 <  A , A <  5, а >  в ,

The Pareto optimal solution of MOSOP model (14) using Fuzzy and Intuitionistic fuzzy multi-objective nonlinear programming technique is given in table 1.

Table 1. Comparison of Optimal solution of MOSOP (14) based on different method

Method	A Х 10 - 4 m 2	A Х 10 - 4 m 2	WT ( A , A2 ) х 102 KN	S x ( A 1 , A 2 ) x 10 - 6 m	S y ( A 1 , A 2 ) x 10 - 6 m
Fuzzy multi-objective nonlinear programming (FMONLP)	2.677489	0.1	5.454979	7.335216	0.1344683
Intuitionistic fuzzy multi-objective nonlinear programming (IFMONLP) £ 1 = 1.2812327, £ 2 = 0.85, £ 3 = 0.2480392	2.767947	0.1	5.635894	7.099601	0.1259712
Intuitionistic fuzzy multi-objective nonlinear programming (IFMONLP) £ 1 = 0.76873962, £ 2 = 1.7, £ 3 = 0.2480392	2.613073	0.1	5.326147	7.512768	0.1410545

Here we get best solutions for the different tolerance ε ₁, ε ₂ and ε ₃ , for non membership function of objective functions. From the table 1, it shows that IFMONLP technique gives better Pareto optimal result in the perspective of Structural Optimization.

• VII.    C onclusions

In view of comparing the intuitionistic fuzzy optimization with fuzzy optimization method, we also obtained the solution of the undertaken numerical problem by fuzzy optimization method given by Zimmermann and intuitionistic fuzzy optimization method given by Angelov. The main objective of this work is to illustrate how IFO technique can be utilized to solve a nonlinear structural problem .The concept of IFO technique allows one to define a degree of rejection, which may not simply be a complement of degree of acceptance. Here we have considered a non-linear three bar truss design problem .In this problem, we find out minimum weight of the structure as well as minimum deflection of loaded joint. The comparisons of results obtained for the undertaken problem clearly show the superiority of intuitionistic fuzzy optimization over fuzzy optimization. The results of this study may lead to the development of effective IFO technique for solving other model of nonlinear programming problem in different field.

C onflict of I nterests

The authors declare that there is no conflict of interests.

A cknowledgement

The authors are grateful for the valuable comments and suggestions from the respected reviewers which have enhanced the strength and significance of our work.