Мультиагентный метод повышения адаптивности и эффективности управления вычислительными ресурсами в реальном времени

Эффективное управление ресурсами (транспортные средства, производственные линии или вычислительные мощности и др.) остаётся ключевой проблемой для систем, где ограниченные ресурсы должны распределяться между конкурирующими задачами. Эта проблема решается в основном методами комбинаторного или эвристического планирования и оптимизации, основанными на пакетной обработке, где задачи и ресурсы известны заранее, а расписание строится без возможности последующей корректировки [1, 2]. Такой подход хорошо работает в предсказуемых и неизменных условиях – например, при планировании производ- ственных циклов с фиксированными заказами или в вычислительных системах (ВС) с определённой нагрузкой.

В процессе роста сложности и динамики таких систем централизованные методы и алгоритмы управления стали встречать серьёзные трудности:

• ■    с увеличением размерности решаемых задач традиционные методы оказываются малоприменимыми из-за комбинаторного роста числа вариантов и резкого увеличения объёма вычислений;

• ■    требуется всё чаще учитывать не только интересы центра, но и отдельных узлов ВС, а также индивидуальные особенности поступающих задач;

• ■    высокая неопределённость и динамика бизнес-процессов приближают их к границе «хаоса», а принятые ранее решения в любой момент могут изменяться;

• ■    жёсткая привязка ресурсов к единому диспетчеру не обеспечивает необходимой масштабируемости и отказоустойчивости – ключевых требований для современных вычислительных и производственных сред.

Для преодоления этих трудностей в ВС в настоящей работе предложен метод, который обеспечивает возможность непрерывной квазиоптимизации временных параметров распределения задач между вычислительными ресурсами (ВР) в реальном времени. В этих целях разработаны модели и методы адаптивных пакетов изменений (патч, от англ. patch ) для последовательных атомарных модификаций расписания, позволяющие точечно сдвигать задачи без их полной отмены, минимизировать потери при перепланировании и поддерживать актуальное состояние системы в реальном времени.

1    Обзор существующих решений

Недостатки централизованных ВС обусловили потребность в разработке распределённых и самоорганизующихся систем, управляемых коллективом автономных роботов, программных агентов, способных принимать согласованные локальные решения, находясь в коммуникации с другими агентами ВС [3, 4]. Такие ВС показывают превосходство в производительности, позволяя принимать решения в реальном времени [5], и обладают более высокой отказоустойчивостью [6].

Рассматриваемое направление получило развитие в Самарской школе мультиагентных (МА) систем [7]. На основе МА моделей сети потребностей и возможностей (ПВ-сетей) и метода компенсаций при взаимных уступках агентов сформулирована концепция эмерджентно-го интеллекта – коллективного искусственного интеллекта (ИИ), возникающего в открытых самоорганизующихся системах с использованием онтологий и МА технологий. Решение сложной задачи при таком подходе строится как процесс самоорганизации программных агентов с конфликтными интересами, которые выявляют и разрешают конфликты в ходе непрерывной конкуренции и кооперации на виртуальном рынке ВС. Разрешение конфликтов осуществляется за счёт переговоров агентов, сопровождающихся взаимными уступками, регулируемыми индивидуальными функциями удовлетворённости, и бонусов-штрафов агентов до достижения состояния консенсуса, отражающего «конкурентное равновесие» агентов (когда ни один из агентов не может улучшить своё состояние). Разработанный подход показал свою эффективность при решении ряда задач управления ресурсами в транспорте, промышленном производстве, цепочках поставок и других применениях [8].

Задача эффективного управления ВР стала особенно актуальной в связи с растущей сложностью решаемых задач, развитием суперкомпьютеров, методов и средств ИИ. В [9] предложена модель суперкомпьютерного кластера, развивающая методы систем массового обслуживания для повышения эффективности вычислений. В этой области разработан и применяется ряд решений на основе МА технологий. В [10] заложена теоретическая основа и проведён ряд исследований децентрализованного управления самоорганизующимися ВС. Однако предложенные в ней модели и методы имеют ограничение, связанное с невозможностью обеспечить максимальную адаптивность в реальном времени.

Известны решения, нацеленные на оптимизацию расписания в реальном времени. В [11] описан алгоритм оптимизации расписания задач NDFS ( Nearest Deadline First Scheduled), исходя из заданного срока их выполнения с учётом их приоритетов. В [12] эта модель дополнена динамическим ранжированием ресурсов и резервным копированием задач на следующий по рангу ресурс, что повышает устойчивость системы к внештатному выходу ресурса из строя. В [13] описан подход к оптимизации расписания FCFS-LRH ( First Come First Served -Left-Right Hole ), нацеленный на минимизацию незаполненных промежутков в расписании.

Примеры решения задач динамического планирования в вычислительных средах приведены в [14-19], варианты применения МА систем для управления ресурсами и их расписаниями - в [20]. Большинство описанных в этих работах алгоритмов опирается лишь на общий приоритет задач и на временное окно, когда бронирование ресурса для задачи имеет смысл, и рассматривается только наиболее позднее возможное планирование задачи. При возникновении локального конфликта происходит полное перепланирование расписания или его участка, что может приводить к излишним и произвольным перестановкам в расписании.

Цель настоящей работы - переработать подход к заданию правил планирования задач и обеспечить более высокую адаптивность.

2    Формализация задачи 2.1    Элементы вычислительной системы и их основные параметры

Моделируемая ВС состоит из двух основных типов сущностей: ресурсов, которые выполняют работу, и задач, которые необходимо выполнить. Эти сущности представляются следующими наборами:

• ■    набор ресурсов R = {rj}, j = 1, J, где J - количество ресурсов;

• ■    набор задач О = { oj, 1, /, где I - количество задач.

• 2.2    Описание задач

  

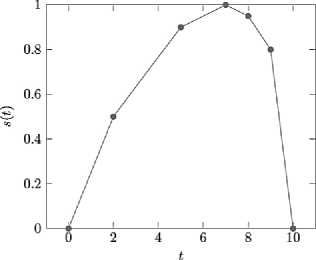
  Рисунок 1 - Пример модели функции удовлетворённости

  
  

• 2.3    Постановка задачи

• 2.4    Модель функции удовлетворённости

Важным условием является то, что в любой момент времени в системе могут происходить непредвиденные события, включая появление новых заказов или отказов в работе ВС, что должно вызывать перераспределение ресурсов и перепланирование работ.

Каждая задача оi из набора О характеризуется длительностью выполнения и моделью функции удовлетворённости. Модель функции удовлетворённости представляет собой набор точек ( t, sf t)), где sf t) - показатель удовлетворённости задачи в случае её выполнения в момент времени t (см. рисунок 1). Функция удовлетворённости может принимать значения в диапазоне s f t) G [0,1]. Временная ось не имеет ограничений. Для удобства восприятия графической информации в данной работе используется упрощённое представление - в секундах, от 0 до 10 включительно.

Необходимо для имеющихся групп ресурсов R и задач О максимизировать целевую функцию S, представляющую собой показатель общей удовлетворённости системы (ПОУС), который включает все задачи и ресурсы: S = ^=г s(ti) , где 1t - время выполнения задачи оi (в случае, если для задачи оt не забронирован ресурс, то считать st = 0).

Модель удовлетворённости представлена в виде равнобедренного треугольника. Такая модель позволяет упростить последующий анализ сложных функций, полученных путём комбинации (сложения, вычитания и пр.) множества других исходных моделей и функционально соответствует зависимости уровня удовлетворённости реальных задач от времени их выполнения.

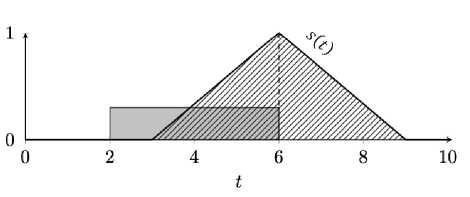
Рисунок 2 - Изображение задачи на графике и её функции удовлетворённости

На рисунке 2 показан график, где в качестве примера на общей временной оси представлена задача длительностью 4 секунды (фигура, заполненная сплошной заливкой) и её функция удовлетворённости (фигура, заштрихованная под углом 45 градусов). В данном примере задача находится в оптимальном положении, при котором время её выполнения соответствует наибольшему из возможных значений её функции удовлетворённости.

3    Традиционный подход к решению задачи 3.1    Описание алгоритма

В числе традиционных алгоритмов планирования и оптимизации выполнения задач [1, 2] лежит принцип: «первый пришёл - первый исполнился». Для МА системы такой принцип часто применяется, и в алгоритмы не включается взаимодействие с другими агентами задач -агент нового заказа анализирует расписание на предмет свободных мест и выбирает наиболее подходящее место, согласно собственной функции удовлетворённости так, чтобы не затронуть другие задачи.

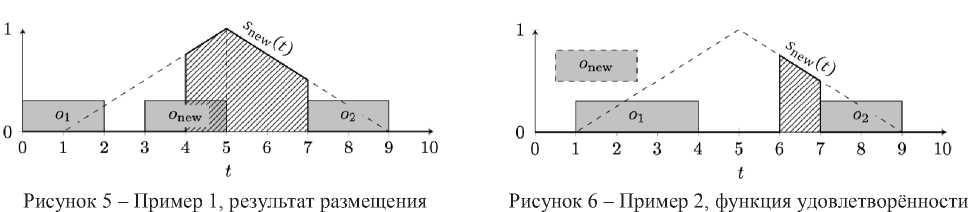
Пример 1 - наиболее благоприятный для этого алгоритма, когда задача o_new может свободно разместиться и выполниться в момент времени t_peak, совпадающий с пиком собственной функции удовлетворённости. На рисунке 3 видно, что свободное пространство, находящееся в диапазоне ненулевого значения функции удовлетворённости, представляет отрезок времени t £ [2, 7] секунд. С учётом длительности выполнения задачи o_new возможное время выполнения задачи находится в пределах t £ [4,7] секунд (рисунок 4). Алгоритм ограничивает функцию удовлетворённости этим промежутком и выбирает наилучшую из возможных позиций для бронирования ресурса. Здесь функция удовлетворённости принимает наибольшее значение в момент времени 5 секунд. Следовательно, агент задачи забронирует ресурс в промежутке времени t £ [3,5] секунд (рисунок 5).

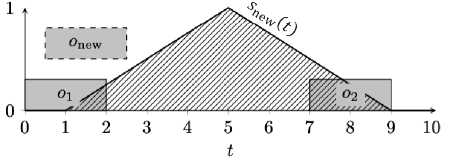
Рисунок 3 - Пример 1, исходная функция удовлетворённости задачи onew

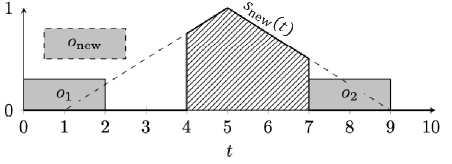
Рисунок 4 - Пример 1, функция удовлетворённости задачи o_{e e w} после её ограничения

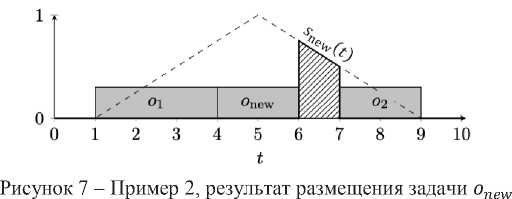
Примере 2 - ограниченная функция удовлетворённости имеет область ненулевых значений t £ [6,7] секунд (рисунок 6). Функция удовлетворённости принимает максимальное значение в момент времени 6 секунд. Следовательно, агент задачи забронирует промежуток времени t £ [4,6] секунд (рисунок 7).

задачи задачи     после её ограничения

• 3.2    Недостаток традиционного алгоритма

В Примере 3 (рисунок 8) одна из задач ( ) из последней конфигурации модели смещена вправо на 0.5 секунды. Это изменение в ВС приводит к резкому ухудшению работы алго- ритма. На рисунке 8 можно видеть три свободных промежутка времени. Первые два – t £ [0,1.5] и t £ [3.5, 5] секунд - имеют продолжительность 1.5 секунды и не могут вместить задачу продолжительностью 2 секунды. Последний промежуток времени (в конце расписа- ния) не имеет ограничения длительности, но на нём невозможно расположить задачу onew так, чтобы она выполнилась в момент времени, соответствующий ненулевому значению функции удовлетворённости.

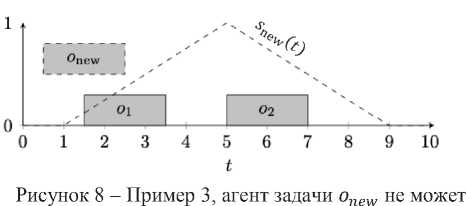
забронировать ресурс

В примере 3 возможно сместить задачи и за счёт частичного снижения их показателя удовлетворённости так, чтобы между ними образовалось пространство в 2 секунды. Это позволит вместить новую задачу и повысить ПОУС, но для этого нужны переговоры, чтобы учесть индивидуальные особенности каждого участника и его предпочтения.

4    Адаптивное формирование расписаний выполнения заданий на вычислительных ресурсах 4.1    Описание предлагаемого метода

Основная задача разрабатываемого метода – сделать процесс распределения ресурса коллективным, с учётом его актуального состояния. Такой алгоритм должен поддерживать возможность смещения задач, уже размещённых в расписании ресурса, и вытеснения и перемещения задач между ресурсами.

Вводятся два дополнительно термина.

• ■    Модификация тоd - атомарное изменение существующего расписания: добавление задачи, сдвиг задачи, вытеснение задачи, перераспределение на другой ресурс и т.д. Модификации не носят контекстуальный характер, они являются лишь составляющими конечного плана изменения расписания – патча.

• ■    Патч рatch - конечный последовательный набор модификаций. Патч носит контекстуальный характер и всегда относится к конкретному ресурсу, он используется как универсальный пакет передачи информации об изменениях расписания конкретного ресурса как между агентами задач в процессе утверждения патча, так и при отправке утверждённого патча агенту ресурса.

Каждая модификация тоПтт патча рaCchm (п = 1, Nт, т = 1, М , Nm - количество модификаций в патче    ℎ , M – количество патчей) вносит изменение в расположение зада чи в расписании и влияет на её показатель удовлетворённости. Изменение показателя удовлетворённости задачи при применении к ней модификации то dт,п составляет Asпт. Изменение ПОУС при применении патча    ℎ составляет Δ     и равно сумме всех измене ний показателей удовлетворённостей задач, вызванных применением модификаций этого патча AS™ tch = Z^As n,m. Процесс формирования патча состоит из следующих этапов.

• 1)    Агент задачи самостоятельно анализирует состояние расписания ресурса и вычисляет наиболее выгодный для системы патч. Здесь «наиболее выгодный» – это такой патч     ℎ , который имеет наибольшее значение прироста ПОУС ∆     среди всех доступных патчей.

• 2)    Агент задачи передает патч другим агентам задач, затронутых этим патчем. Другие агенты задач могут принять патч или принять решение о смене ресурса и сообщить об этом агенту задачи, передавшему патч. При принятии решения о смене ресурса агент задачи, рассчитавший патч, рассчитывает его заново и сообщает об изменениях другим агентам задач. Этот цикл длится до тех пор, пока все агенты задач, затронутых патчем, не будут удовлетворены актуальным патчем либо сообщат о смене ресурса.

• 3)    Агент задачи, рассчитавший патч, передаёт утверждённый патч агенту ресурса.

• 4)    Агент ресурса применяет патч, и, в случае успешного применения, уведомляет всех затронутых агентов задач об успешном применении патча. В случае неудачи агент ресурса сообщает агенту задачи причину ошибки применения патча. Ошибки в применении патча могут возникать по различным причинам, например, устаревшая информация о расписании у агента задачи. Агент задачи может либо принять меры по разрешению проблемы, если такая возможность есть, либо перейти к рассмотрению другого ресурса.

• 4.2 Алгоритм расчёта наиболее выгодного патча

• 4.2.1    Формализация задачи

В контекст задачи входят:

• ■    ресурс г и его расписание s hhd d и I е;

• ■    набор задач О = о,, 1,I, уже находящихся в расписании s chddиI е, где I - количество задач в расписании;

• ■    задача o_new, не находящаяся в расписании s chd d и I е, которую необходимо разместить.

Новую задачу можно разместить между любыми двумя задачами или по краям расписания. При этом можно сместить любую из размещённых в расписании задач так, чтобы забронированные ими временные участки не пересекались. Всего вариантов размещения новой задачи относительно находящихся в расписании задач I + 1, где I - количество задач, уже размещённых в расписании. Для каждого варианта размещения рассматривается до вариантов сдвига других задач: А" = (I + 1) • Z =i Т, где Т- - количество опорных временных точек модели функции удовлетворённости задачи . Область возможных решений представляет гиперповерхность в пространстве размерности I + 2, где:

• ■    ось ах i s ,, i = 1, I задаёт время t j , к которому выполнится задача о;,

• ■    ось xxis_{} +i} задаёт время n _new, в которое выполнится размещаемая задача n _eew;

• ■    ось xxis_{} +} 2 отражает приращение ПОУС AS™_{tc h} при расположении задач в расписании в соответствии со значениями остальных осей.

• 4.2.2    Описание алгоритма

Изображение гиперповерхности для I = 1 представлено на рисунке 9. Проекция гиперповерхности на гиперплоскость AS = 0 (заштриховано) представляет область допустимых вариантов размещения задач в расписании.

Задача алгоритма сводится к поиску патча с максимальным 1 приращением ПОУС. На рисунке 9 максимальному приращению ПОУС соответствует патч, устанавливающий время выполнения размещённой задачи ^ = 1 секунда, а новой задачи t_new = 4 секунды.

Если нет ни одного варианта, для которого AS™tch >0, то добавление задачи onew в расписание считается невозможным.

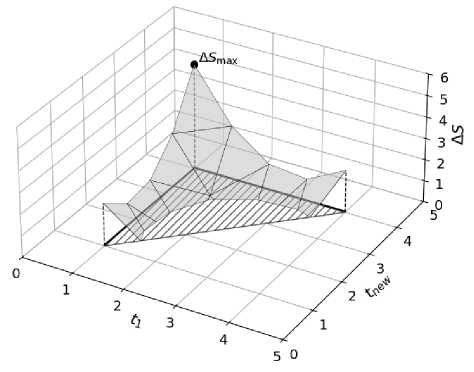
Рисунок 9 – Гиперповерхность возможных решений при / = 1

Входными данными являются: состояние расписания ресурса; параметры новой задачи; параметры задач, размещённых в расписании. Результат работы алгоритма – патч с наибольшим приращением ПОУС среди всех возможных патчей.

Для каждого варианта размещения новой задачи в расписании итеративно применяются следующие этапы алгоритма.

• 1)    Для выбранного размещения рассчитывается модель сдвига окружающих задач.

• 2)    Из полученной модели сдвига задач и их функций удовлетворённости рассчитывается функция стоимости сдвига, отражающая зависимость потери в ПОУС от величины сдвига.

• 3)    Рассчитывается функция приращения ПОУС как разница функции удовлетворённости новой задачи и функции стоимости сдвига.

• 4)    Составляется патч, включающий добавление новой задачи и сдвиг окружающих задач в соответствии с максимальным значением функции приращения ПОУС.

Затем, из всех рассчитанных патчей выбирается один – с наибольшим значением приращения ПОУС.

Схема алгоритма представлена на рисунке 10.

Сдвиг задач, начиная с задачи вперёд – это такое изменении времени бронирования A ^ ^{е8 1 п} > 0 задачи o_n, при котором время бронирования t ^ ^{e 8 1 п} каждой последующий задачи о_т, т > п в расписании изменяется на минимально возможное значение для выполнения условия ^^е81п > t e_1 где t efA — это момент времени, в который выполнится задача о_т _ _ь предшествующая задаче , если она будет принята к исполнению в момент времени     .

Условия сдвигов назад и вперёд представлены формулами 1 и 2 соответственно.

f_At n ^e8 ' ^п < 0

⎪

Мт <  <-т+1

A М ^{8 n} • 0

v т п п

f A^ ⁸ ' ⁿ > 0

⎪

• <    ^L m     >  т_ _ 1

At^ ⁸ '" - 0

• <    m

• 4.2.3    Расчёт функции стоимости сдвига

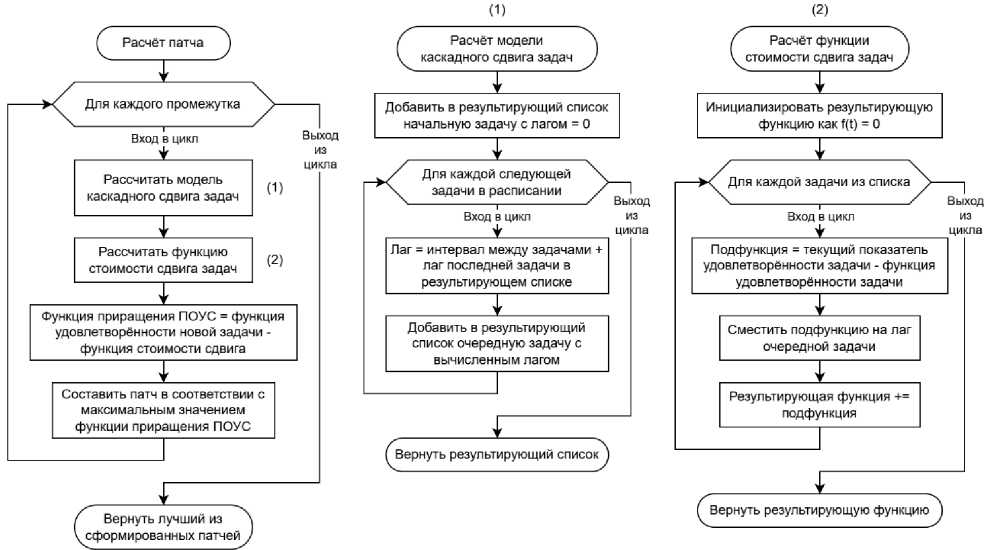
Рисунок 10 – Схема алгоритма расчёта и выбора наилучшего патча

В Примере 4 (рисунок 11) представлена работа алгоритма расчёта функции стоимости сдвига для задач и , где – функция удовлетворённости задачи , – функция удовлетворённости задачи о₂ . Обе задачи находятся в оптимальном положении. Задачи сдвигаются в сторону увеличения времени их брони (вправо), освобождая пространство перед задачей .

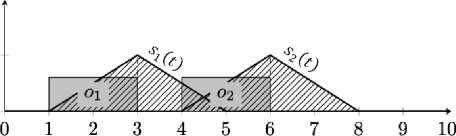
Рисунок 11 – Пример 4, функции удовлетворённости задач

Согласно изначальному расписанию задача должна начать обрабатываться в момент времени 1 секунда. Если новую задачу возможно разместить так, чтобы она выполнилась в этот же момент времени, то задача не сдвигается и стоимость этого нулевого сдвига составит №_{shif t}(1) = S i (3) - s i ⁽ 3) = 1 - 1 = 0.

Отрезок времени t G [1,2] секунд можно освободить, переместив только задачу о.. При этом она встанет вплотную к задаче о₂. Стоимость сдвига составит LS _shif _t(2) = s₁(3) — s ₁ (4) = 1 — 0.5 = 0.5. Функция стоимости сдвига (рисунок 12) заштрихована под углом 135 градусов. Чтобы освободить участок t G [2,3] секунд, понадобится сдвигать обе задачи (см. условия сдвига (1) и (2) в разделе 4.2.2). Функция стоимости сдвига равна сумме изменений их показателей удовлетворённости &S_sh if_t(3) = (s АЗ) — s А5)) + (s ₂(6) — s ₂(7)) = (1 — 0) + (1 — 0.5) = 1.5 (рисунок 13). При дальнейшем смещении задачи о₁ функция удовлетворённости не будет оказывать влияния на результирующую, т.к. значение её функции удовлетворённости будет неизменно равно нулю (рисунок 14). Здесь AS_{s h}if _t(4) = (s ₁(3) — s ₁(6)) + (s ₂(6) — s ₂(8)) = (1 — 0) + (1 — 0) = 2. Дальнейшее смещение не повлияет на значение функции стоимости сдвига, т.к. значения обеих функций удовлетворённости неизменно будут равны нулю (рисунок 15).

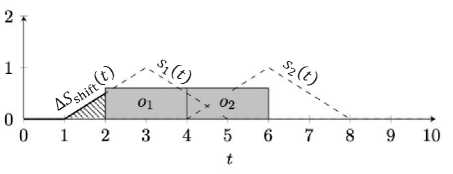
Рисунок 12 – Пример 4, функция стоимости сдвига для t £ [1,2]

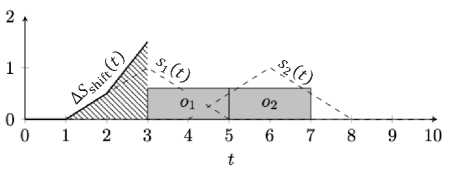
Рисунок 13 – Пример 4, функция стоимости сдвига для t £ [1,3]

> 01

ОЗ '

123456789 10

t

Рисунок 14 – Пример 4, функция стоимости сдвига для t £ [1,4]

123456789 10

t

Рисунок 15 – Пример 4, полностью рассчитанная функция стоимости сдвига

• 4.2.4    Расчёт функции приращения ПОУС

Разница между функцией удовлетворённости     новой задачи     и функцией стоимости сдвига задач Δ    , находящихся в расписании, покажет приращение ПОУС Δ при применении патча, содержащего модификации добавления новой задачи и смещения размещённых.

Если в расписании присутствуют задачи по обе стороны от вставки, то функция стоимости сдвига Δ     рассчитывается из двух компонент: левосторонней Δ     и правосторонней Δ    . Работа алгоритма расчёта приращения ПОУС представлена на примере 5 с од ним отличием от примера 4: задача onew размещается между задачами ох и о2 (рисунок 16). Результат вычисления обеих компонент функции стоимости сдвига представлен на рисунке 17. Правосторонняя функция стоимости сдвига отражает потерю в ПОУС при сдвиге времени начала обработки задачи . Начало обработки задачи будет совпадать с временем окончания обработки добавляемой задачи onew. Функция удовлетворённости также привязана к времени окончания обработки задачи. При рассмотрении правосторонней функции стоимости сдвига разница между snew и s 2 будет отражать приращение ПОУС в зависимости от расположения задач     и .

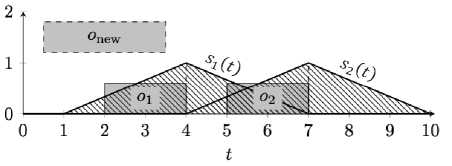
Рисунок 16 – Пример 5, функции удовлетворённости задач

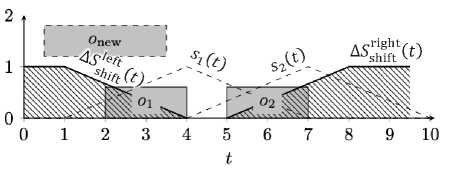
Рисунок 17 – Пример 5, подготовленные к объединению функции стоимости сдвига

В отличие от правосторонней функции стоимости сдвига левосторонняя отражает потерю в ПОУС при сдвиге времени окончания обработки задачи и выбранном начале времени обработки задачи onew. Чтобы две функции стоимости сдвига можно было сложить, необходимо предварительно сместить левостороннюю компоненту вперёд на промежуток, равный длительности новой задачи onew (рисунок 18). Результат сложения обеих частей функции стоимости сдвига и функция удовлетворённости snew представлены на рисунке 19.

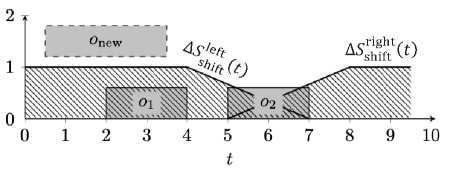
Рисунок 18 – Пример 5, компоненты функции стоимости сдвига для обоих направлений

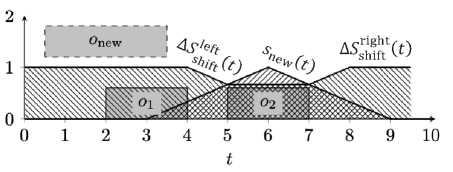
Рисунок 19 – Пример 5, функция стоимости сдвига (штриховка 135°) и функция удовлетворённости ^snew новой задачи onew (штриховка 45°)

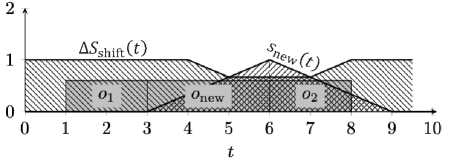
Рисунок 20 – Пример 5, результат размещения новой задачи

На данном этапе становится видно, как выглядит разница snew и функции стоимости сдвига. Задача onew размещается в соответствии с максимальным значением их разности (рисунок 20).

5 Прототип системы управления вычислительными ресурсами

Акторная система реализована на языке Python 3.13 с использованием библиотек:

• ■    thespian - реализация модели акторов для создания распределённых и многопоточных систем;

• ■    pydantic - валидация данных и генерация конструкторов классов;

• ■    loguru - журналирование работы системы;

• ■    pytest - модульное тестирование;

• ■    pickle - сериализация сообщений между агентами.

• 5.1    Архитектура мультиагентной системы

Роль управления агентами полностью делегирована от центрального объекта акторной системы специальному агенту-менеджеру, который, в отличие от объекта акторной системы, находится в потоке, не связанном с системной оболочкой, что позволяет ему обрабатывать входящие сообщения, не блокируя интерфейс программы. Акторная система выполняет две задачи: инициализация агента-менеджера при запуске модели и чтение стандартного потока ввода. При вводе команд в стандартный поток акторная система отправляет сообщение с текстом команды актору-менеджеру и переходит в режим ожидания следующей команды. Это позволяет вносить изменения в ВС параллельно с протекающим в ней активным процессом, используя единый интерфейс взаимодействия с ВС (консоль программы, объединяющая стандартные потоки ввода и вывода), что упрощает проведение экспериментов.

Агент-популятор предназначен для автоматизации проведения множественных последовательных экспериментов. Он перебирает различные варианты конфигурации ВС, запускает акторную систему с выбранными параметрами, собирает данные, записывает в таблицу и повторяет процесс для каждой комбинации входных параметров.

Основные агенты модели – это агенты задач и агенты ресурсов. Схема иерархии агентов представлена на рисунке 21.

Агент ресурса хранит свойства ресурса и его текущее расписание, которое представляет собой хранящий упорядоченный список непересекающихся временных интервалов, представленных в виде объектов броней. Класс расписания реализует все необходимые функции для анализа расписания на свободные промежутки времени, валидацию и применение патчей, поиск брони по её свойствам или временной точке, визуализации текущего состояния. Класс брони хранит информацию о временном промежутке бронирования ресурса, информацию о задаче, а также информацию о соседних бронях, если бронь помещена в расписание.

Агент задачи хранит свойства задачи, текущее состояние бронирования ресурса и информацию о всех доступных ресурсах. В рамках проведения эксперимента использованы две модели поведения агента задачи – пассивная и активная, алгоритмы поведения которых рассмотрены в подразделах 3.1 и 4.2.

Класс агента библиотеки thespian дополнен функциональностью,

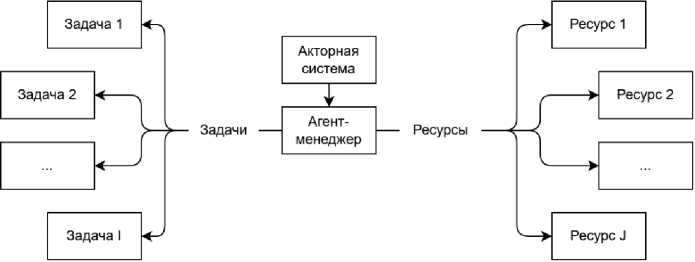
Рисунок 21 – Схема иерархии агентов

позволяющей организовывать более сложные цепочки коммуникаций агентов.

• ■    Привязка к агенту-менеджеру . Эта модификация позволяет агенту запрашивать информацию о текущем состоянии ВС, например, количество агентов выбранного типа.

• ■    Возможность широковещательной отправки сообщений . Агент может отправить сообщение конкретному агенту или группе агентов, выделив их по какому-либо признаку.

• ■    Сообщение-запрос . Это модифицированный вид сообщения с внедрённой в класс агента логикой, требую

щей от получателя ответить отправителю сообщением-ответом.

• ■    Множественный запрос . Эта модификация позволяет связывать функцию для отложенной обработки ответа не с единственным запросом, а с группой запросов.

• ■    Отложенный ответ . Эта модификация позволяет агенту-получателю сообщения-запроса не отвечать агенту-отправителю немедленно. Агент сохраняет в своём состоянии данные запроса и его содержание. Агент может проверить наличие отложенных ответов и отправить агенту-отправителю сообщение-ответ.

5.2 Протокол взаимодействия агентов

Класс агента получил дополнительные функции ведения журнала, счётчика и ограничителя отправленных сообщений, не позволяющего агентам бесконечно обмениваться цикличными сообщениями.

При запуске МА системы восстанавливается состояние акторной системы по предварительно заданной конфигурации. Считывается конфигурационный файл, и для каждого описанного агента отправляется агенту-менеджеру сообщение с данными для инициализации нового агента. Схема взаимодействия агентов при запуске модели представлена на рисунке 22.

Агент-менеджер выступает в роли посредника, так как только он хранит информацию о всех активных агентах модели. Агент-менеджер включает агента модели в список активных агентов после получения от него сообщения о готовности к работе и сообщает ему

Пользователь Акторная система Агент-менеджер Агент модели

Инициализируй модель

Прочитай конфигурацию

Создай агента модели

Инициализация

Готов

Выполни сценарий запуска

Рисунок 22 – Процесс восстановления состояния акторной системы по заданной конфигурации

команду для выполнения сценария запуска.

Данное разделение процесса служит для предотвращения двух неблагоприятных случаев: агент, не завершивший инициализацию, получает сообщение от другого агента модели; агент модели получает сообщение от агента, которого нет в списке активных агентов. Таким образом гарантируется, что отправитель и получатель любого сообщения между агентами модели включены в список активных агентов.

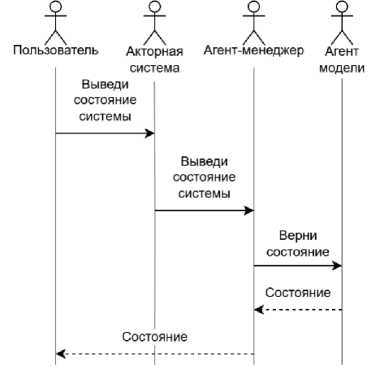
пользовательской команды

Новая задача

Рисунок 23 - Процесс выполнения

Предоставь респисание

Респисание

Подготовь патч

Прими патч

opt /

[Агент размещённой задачи не принял патч]

Не принял патч

Скорректируй патч

Прими патч

Принял патч

Примени патч

° pt /

[Ошибка применения патча]

Ошибка

Скорректируй патч

Прими патч

Принял патч

Примени патч

Применил патч

Применил патч

Рисунок 24 - Процесс формирования и принятия патча

Взаимодействие МА системы с пользователем также выполняется через агента-менеджера (см. рисунок 23).

• 5 .3 Формирование и применение патча

Чтобы забронировать ресурс, агент задачи (агент-инициатор) запрашивает информацию о расписании у агента ресурса и рассчитывает патч, включающий добавление собственной задачи в расписание (рисунок 24). Если патч содержит изменения состояния других задач, то агент-инициатор направляет им патч на просмотр. Агент задачи может принять либо отвергнуть патч, в зависимости от своей модели поведения. Сообщение о непринятии патча содержит причину отказа, которая используется для его корректировки.

Если все затронутые агенты задач приняли патч, то его финальная версия направляется агенту ресурса, который валидирует патч на возможность его применения. Если применение патча невозможно, то агент ресурса сообщает об этом агенту-инициатору, указывая причину и актуальное состояние ресурса.

После корректировки патча агент-инициатор отправляет его на просмотр другим включённым в патч агентам задач. После принятия патча, агент-инициатор снова отправляет патч агенту ресурса. Если агент ресурса определит патч валидным, то он применит этот патч на собственном расписании и уведомит всех затронутых агентов задач об изменении их положения в расписании.

Метод разрешения конфликтов посредством переговоров между агентами потенциально может приводить к образованию замкнутых циклов взаимодействий, известных как взаимные блокировки.

Существует два сценария, ведущих к цикличности в переговорах: отказ агента задачи от предлагаемого патча и отказ агента ресурса от применения патча.

Отказ агента задачи возможен при наличии у него информации о другом ресурсе, который агент оценивает как потенциально более предпочтительный, исходя из возможностей реализации своей функции удовлетворённости. Такой агент немедленно прекращает участие в текущем процессе согласования и покидает соответствующий ресурс. В переговорах остаются те агенты, которые согласны с предложенными условиями.

Отказ агента ресурса от применения патча возможен в ситуации, когда предоставленный патч был сформирован на ос- нове устаревшей информации о состоянии ресурса. В этом случае агенту задачи направляется обновлённая информация о состоянии ресурса, на основании которой он пересматривает свою стратегию.

Применение патча - синхронный и атомарный процесс: в каждый момент времени только один агент задачи может успешно применить изменения к расписанию ресурса. Это означает, что в случае поступления нескольких конкурирующих патчей будет гарантировано, что один из них будет применён первым, а остальные получат информацию об изменившемся состоянии ресурса. Благодаря этому агенты, получив обновлённые данные, гарантированно смогут применить патч на ресурсе.

6 Вычислительный эксперимент

Сравнение двух методов между собой производилось путём тестирования, которое выполнял специальный агент. Ему передавалась информация о варьируемых элементах конфигурации ВС: пределы варьирования, шаг варьирования или заранее заданные варианты:

• ■    тип поведения агента задачи - активный или пассивный (пассивное поведение соответствовало следованию традиционному алгоритму, активное - предлагаемому);

• ■    количество задач (от 5 до 25 задач с шагом 5);

• ■    длительность задач (от 2 до 6 часов с шагом 1 час):

• ■    продолжительность модели функции удовлетворённости задач (для всех задач модель функции удовлетворённости имела форму равнобедренного треугольника: длина основания треугольника является продолжительностью модели функции удовлетворённости задачи и варьировалась в промежутке от 3 до 12 часов с шагом 3).

Агент-популятор поочерёдно воспроизводил состояние системы для каждой из возможных комбинаций параметров, все задачи имели одинаковые исходные данные за исключением благоприятного времени выполнения задачи. После завершения переговоров между агентами задач и ресурсов агент-популятор запрашивал их показатели удовлетворённости, на этой основе получал информацию о количестве задач, успешно зарегистрировавших ресурс, и рассчитывал ПОУС.

Каждый запуск ВС имеет случайный фактор, вызванный невозможностью предсказать, в каком порядке будут обрабатываться сообщения агентов, запущенных одновременно. Чтобы компенсировать влияние случайного фактора каждая конфигурация ВС воспроизводилась несколько раз. Всего проведено 5 последовательных экспериментов.

На рисунке 25 показано распределение ПОУС, где видно, что мода распределения у предлагаемого (активный тип поведения агентов задач) алгоритма выше, чем у традиционного (пассивный тип поведения агентов задач).

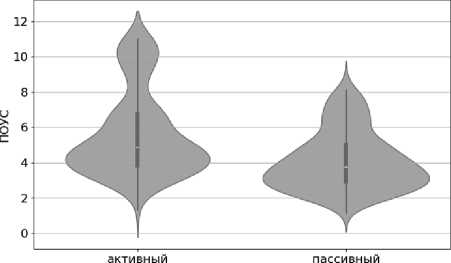
Тип поведения

Рисунок 25 - Распределение ПОУС для активного и пассивного типов поведения агентов задач

На рисунках 26 - 28 показаны зависимости ключевых показателей ВС - ПОУС и количество агентов задач, успешно забронировавших ресурс от варьируемых параметров системы.

На приведённых графиках видно, что адаптивный метод показывает на 25-30% лучший результат по сравнению с традиционным. Это объясняется большей гибкостью предлагаемого алгоритма, который способен найти способ вместить в расписание задачу и повысить

ПОУС, в то время как традиционный алгоритм сочтёт невозможным добавление новой зада- чи в расписание.

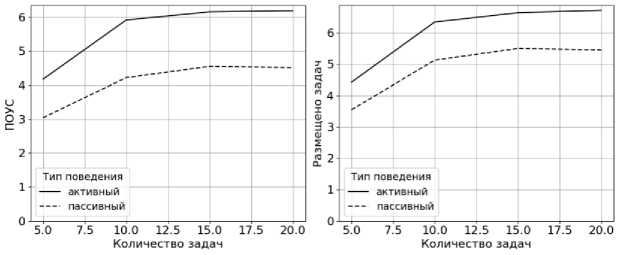
Рисунок 26 – Зависимость ключевых показателей от количества задач в системе

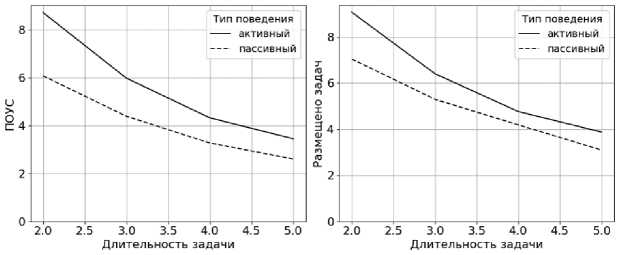
Рисунок 27 – Зависимость ключевых показателей от длительности задач

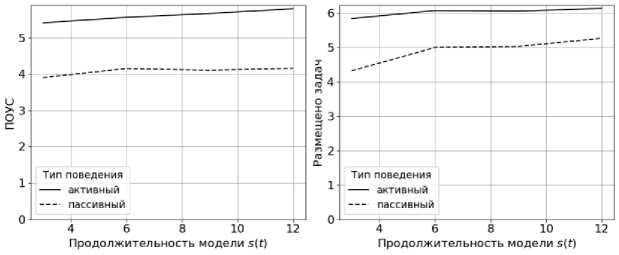
Рисунок 28 – Зависимость ключевых показателей от продолжительности модели функции удовлетворённости

Заключение

Разработанный адаптивный метод управления ВР на основе МА технологий ПВ-сетей имеет значительный потенциал для повышения эффективности перераспределения задач в реальном времени. В отличие от алгоритмов, ограниченных пакетным планированием, предложенный метод с адаптивными патчами позволяет выполнять модификации расписания, минимизируя потери при перепланировании и сохраняя устойчивость ВС. Преимуществами метода являются:

• ■    высокая адаптивность, т.к. допускается изменять любые ранее принятые решения по включению и сдвигам заказов в расписания ВР;

• ■    коллективное принятие решений, при котором агенты задач анализируют расписание не только с позиции собственных интересов, но и потенциально учитывают влияние изменений на показатель общей удовлетворённости системы;

• ■    гибкость и масштабируемость, достигаемые за счёт децентрализованного взаимодействия агентов;

• ■    подтверждённое вычислительным экспериментом повышение ПОУС на 25-30% за счёт применения адаптивных патчей по сравнению с традиционным методом.

Предложенный метод обладает адаптивностью для интеграции новых функций. Его развитие открывает перспективы практического применения для задач динамического распределения ресурсов в вычислительных, производственных и логистических системах.