Multiobjective Multipath Adaptive Tabu Search for Optimal PID Controller Design
Автор: Deacha Puangdownreong
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 8 vol.7, 2015 года.
Бесплатный доступ
The multipath adaptive tabu search (MATS) has been proposed as one of the most powerful metaheuristic optimization search techniques for solving the combinatorial and continuous optimization problems. The MATS employing the adaptive tabu search (ATS) as the search core has been proved and applied to various real-world engineering problems in single objective optimization manner. However, many design problems in engineering are typically multiobjective under complex nonlinear constraints. In this paper, the multiobjective multipath adaptive tabu search (mMATS) is proposed. The mMATS is validated against a set of multiobjective test functions, and then applied to design an optimal PID controller of the automatic voltage regulator (AVR) system. As results, the mMATS can provide very satisfactory solutions for all test functions as well as the control application.
Multiobjective Multipath Adaptive Tabu Search, PID Controller, Metaheuristics, Control System Optimization
Короткий адрес: https://sciup.org/15010742
IDR: 15010742
Текст научной статьи Multiobjective Multipath Adaptive Tabu Search for Optimal PID Controller Design
Published Online July 2015 in MECS DOI: 10.5815/ijisa.2015.08.07
Real-world engineering optimization problems are often concern multiple design objectives under complex constraints. In fact, different objectives often conflict each other. This makes truly optimal solutions may not exist at all and some compromise and approximations are often needed. Moreover, many real-world engineering problems are often NP-hard, which means that there is no known efficient algorithm which can be used for solving such problems effectively. Classical optimization methods often face difficulties for solving them. Metaheuristics, a kind of approximate methods, have been widely used as efficient tools for solving such the optimization problems. Several metaheuristic algorithms have been proposed in dealing with this kind of optimization. By literatures, there are many review articles and excellent textbooks [1,2,3,4,5,6]. Among those, tabu search (TS) [7,8] proposed by Glover is one of the most efficient memory based metaheuristic methods. The TS is considered as a class of singlesolution based metaheuristic algorithms having exploitation (intensification) property. Due to this, the original TS often faces the local entrapment (deadlock) problems. The modified versions of the original TS have been consecutively launched to improve its exploration (diversification) property including reactive tabu search (RTS) [9,10], parallel tabu search (PTS) [11,12,13], modified tabu search (MoTS) [14,15,16] and probabilistic tabu search (PrTS) [17,18,19].
One of the modified versions of the original TS is called the adaptive tabu search (ATS) [20,21]. For the ATS, the performance of TS has been enhanced by additional adaptive search radius mechanism to accelerate the search process, and backtracking mechanism to escape from local solution entrapment. By literatures, the ATS has been successfully applied to various real-world engineering problems, for example, power system protection [22], system and model identification [23,24], control synthesis [25,26] and signal processing [27]. Moreover, the convergence property of the ATS has been proved [28,29]. In 2008, multipath adaptive tabu search (MATS) has been proposed [30,31] with search performance assessment to improve its exploitation and exploration properties. The MATS has been successfully applied to various real-world engineering problems including system and model identification [32] and control system design [33,34,35]. In addition, the convergence proof of the MATS has been analyzed and reported [32]. However, all applications of the MATS are considered as a class of single objective optimization problems.
In metaheuristic optimization context, multiobjective problems are typically much more difficult and complex than single objective ones such as a problem of upgrading to the next generation wireless network (NGWN) [36]. In a multiobjective problem, there are multiple optimal solutions forming the so-called Pareto front. The challenge of problem is how to form the Pareto front containing a set of optimal solutions for all objective functions.
In this paper, the multiobjective multipath adaptive tabu search (mMATS) is proposed to solve multiobjective optimization problems. The performance of the mMATS is evaluated against a set of multiobjective test functions. Then, the proposed mMATS is applied to design an optimal PID controller in an automatic voltage regulator (AVR) system considered as bi-objective optimization problem. This paper consists of five sections. After an introduction provided in section 1, the brief algorithms of TS, ATS and MATS, and the proposed mMATS algorithms are described in section 2. The performance evaluation of the mMATS against a set of multiobjective test functions are performed in section 3. Application of the mMATS to bi-objective PID controller design in AVR system is illustrated in section 4, while conclusions are given in section 5.
-
II .Multiobjective Multipath Adaptive Tabu Search Algorithms
To understand and extend the MATS from single optimization to mMATS for solving multiobjective problems, algorithms of the TS, ATS and MATS are briefly reviewed. Then, the Pareto optimality and algorithms of the proposed mMATS are described.
-
A. Tabu search
Proposed by Glover [7,8], the tabu search (TS) is based on the neighborhood search with memory list called the tabu list (TL). The TL is used to store the visited solutions and conducted as an aspiration criteria when the local entrapment occurs. The original TS search process begins the search with some random initial solutions belonging to a neighborhood search space. All solutions in neighborhood search space will be evaluated via the objective function as deterministic manner. The solution giving the minimum objective value is set as a new starting point of next search round and kept in the TL. A brief algorithm of the TS can be represented by the pseudo code as shown in Fig. 1.
-
B. Adaptive tabu search
The adaptive tabu search (ATS) is one of the modified versions of the original TS launched in 2004 [20,21]. The search process of the ATS is based on the neighborhood search with TL memory list to record all visited solutions in random manner. The ATS possesses two distinctive mechanisms called the backtracking (BT) and the adaptive radius (AR) mechanisms. The BT mechanism regarded as the diversification strategy is conducted to escape local entrapments, while the AR mechanism considered as the intensification strategy is used to speed up the search process. Convergence proof and performance evaluation of the ATS have been reported [28,29]. A brief algorithm of the ATS can be represented by the pseudo code as shown in Fig. 2.
-
C. Multipath adaptive tabu search
The multipath adaptive tabu search (MATS) has been firstly proposed in 2008 [30,31]. Using the ATS as a search core, the MATS consists of three components called partitioning mechanism (PM), sequencing mechanism (SM) and discarding mechanism (DM), respectively. The MATS starts with using many ATS paths. The PM is activated to decompose the entire search space into sub search spaces. The PM also defines explicit search boundaries, each of which is given an individual initial solution and an independent ATS path. The SM is then conducted as the time-sharing strategy to organize the ATS paths to run one-by-one. During the operation of the SM, the DM is activated to stop some low-quality search paths in order to speed up the search process. The PM, SM and DM mechanisms together help to improve the diversification property of the MATS. The convergence proof of the MATS has been analyzed and reported [32]. A brief algorithm of the MATS can be represented by the pseudo code as shown in Fig. 3.
Objective function f ( x ), x = ( x 1 ,^,x d ) T ,
Search space Ω , Tabu list (TL),
Randomly generate initial solution x 0 within Ω ,
Evaluate f ( x 0) via given objective function.
While (Termination criteria)
Deterministically generate neighborhood solutions x ’ ,
Evaluate f ( x ’ ) via given objective function,
Find the best neighborhood solution x *,
If f ( x *)< f ( x 0) Then keep x 0 into TL and update x 0 = x *,
Otherwise keep x * into TL,
If local entrapment occurred Then activate aspiration criteria, End While
Best solutions found.
-
Fig. 1. Pseudo code of the TS algorithm.
Search space Ω , Tabu list (TL), Search radius R ,
Randomly generate initial solution x 0 within Ω ,
Evaluate f ( x 0) via given objective function.
While (Termination criteria)
Randomly generate neighborhood solutions x ’ , Evaluate f ( x ’ ) via given objective function, Find the best neighborhood solution x *,
If f ( x *)< f ( x 0) Then keep x 0 into TL and update x 0 = x *, Otherwise keep x * into TL,
If local entrapment occurred Then activate BT mechanism, If search closes to local solutions Then invoke AR mechanism to reduce R by adjusting R = µ R , 0< µ <1.
End While
Best solutions found.
-
Fig. 2. Pseudo code of the ATS algorithm.
Objective function f x ), x = ( x 1 ,^,xd ) T ,
Initialize ATS i ,_,ATS k ,
Search space Ω , Tabu list (TL), Search radius R ,
Activate PM to decompose О into ® b^, ® d ,
Randomly generate initial solution x 0 within № 1 ,...,^ ,
Evaluate f ( x 0) via given objective function.
While (Termination criteria)
Invoke SM:
For ( i = 1: k )
Start ATS i (other ATS paths are in wait state) by randomly generate neighborhood solutions x ’ , Evaluate f ( x ’ ) via given objective function, Find the best neighborhood solution x *, If f ( x *)< f ( x 0) Then keep x 0 into TL and update x 0 = x *, Otherwise keep x * into TL,
If local entrapment occurred Then activate BT mechanism, If search closes to local solutions Then invoke AR mechanism to reduce R by adjusting R = µ R , 0< µ <1.
Activate DM once the conditions are satisfied to reduce low-quality search paths.
Update i = i+ 1,
End For
End While
Best solutions found.
-
Fig. 3. Pseudo code of the MATS algorithm.
-
D. Pareto optimality
According to the optimization context [1,2,3], multiobjective optimization problem can be expressed in (1), where f(x) is the multiobjective function consisting of f1(x),..., fn(x), n > 2, gj(x), j = 1, 2,^,m, is the inequality constraints and hk(x), k = 1, 2,^,p, is the equality constraints. The optimal solutions, x*, is ones can make f(x) minimum and make both gj(x) and hk(x) satisfied.
min f(x) = {f1 (x), f2 (x), •-, fn (x)} subject to gj (x) < 0, j = 1, ^, m - hk(x) = 0, k = 1,...,p
Based on the Pareto optimality [37,38,39], a solution vector, u = ( u 1,..., un ) T e S , is said to dominate another solution vector v = ( v i,..., vn ) T , denoted by u ^ г , if and only if u i < v i for V i e {1,..., n } and for 3 i e {1,..., n }: u i < v i . This implies that no component of v is smaller than the corresponding component of u , and at least one component of u is strictly smaller stated in (2).
V i e {1,..., n } : u i - < v i A3 i e {1,..., n } : u i < v i (2)
A solution x * e S is called a non-dominated solution if no solution can be found that dominates it. In other words, a solution x * e S is Pareto optimal if for every x e S , f ( x ) e F does not dominate fx *) e F , that is fx *) ^ fx ). For a given multiobjective optimization problem, the Pareto optimal set is defined as P * stated in (3). The Pareto front PF * of a given multiobjective optimization problem can be defined as the image of the Pareto optimal set P * expressed in (4).
P* = { x e F | 3 x * e F : f ( x *) ^ f ( x ) (3)
PF * = { s e S 1 3 s * e S : s * ^ s (4)
E. Multiobjective multipath adaptive tabu search
The multiobjective multipath adaptive tabu search (mMATS) is presented. The MATS algorithm can be modified to minimize the f ( x ) in (1). The convergence property of the mMATS can be hold due to that of the MATS. The mMATS algorithm is represented by the pseudo code as shown in Fig. 4. Multiobjective function f ( x ) in (1) will be simultaneously minimized according to the equality and inequality constraints. The best solution found in each iteration will be checked. If it is a nondominated solution, it will be sorted and stored into the Pareto optimal set P* . After the search terminated, the solutions stored in P* will be used to perform the Pareto front PF* . Solutions appeared on the PF* are the optimal solutions of the problem of interest.
with discontinuous front is expressed in (7), where g and x i in functions ZDT2 and ZDT3 are the same as in function ZDT1. For ZDT4, it is stated in (8) with convex front but more specific.
Activate PM to decompose Q into ® i ,^, ® d ,
Randomly generate initial solution x 0 within ® i ,^, ® d , Evaluate f ( x 0) via given objective function f ( x ).
While (Termination criteria)
Invoke SM:
For ( i = 1: k )
Start ATS i (other ATS paths are in wait state) by randomly generate neighborhood solutions x ’ , Evaluate f ( x ’ ) via given objective function f ( x ), Find the best neighborhood solution x * and check if it is Pareto optimal (non-dominated solution), sort and store it into the Pareto optimal set P* .
If f ( x *)< f ( x 0) Then keep x 0 into TL and update x 0 = x *, Otherwise keep x * into TL,
If local entrapment occurred Then activate BT mechanism, If search closes to local solutions Then invoke AR mechanism to reduce R by adjusting R = ^ R , 0< ^ <1.
Activate DM once the conditions are satisfied to reduce low-quality search paths.
Update i = i+ 1,
End For
Sort and find the current Pareto optimal solutions.
End While
Pareto optimal solutions are found and
Pareto front PF* is performed..
Fig. 4. Pseudo code of the mMATS algorithm.
f_(X) = x1, f 2(x) = g (1 - 7f J g ),
g = 1 +
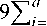
2 xi
d - 1
X i e [0,1], i = 1, ^ ,30
f1( x) = x1, f1(x) = x1,
f 2 ( x ) = g | 1
f 1
g
( f2 (x) = g 1
I
—
/f l — f L sin(10 ^f 1 ) gg
A
-
III. Performance Evaluation
To perform its effectiveness, the mMATS is evaluated against several multiobjective test functions. In this section, a set of multiobjective test functions, search parametric studies and evaluation results are illustrated.
-
A. Set of multiobjective test functions
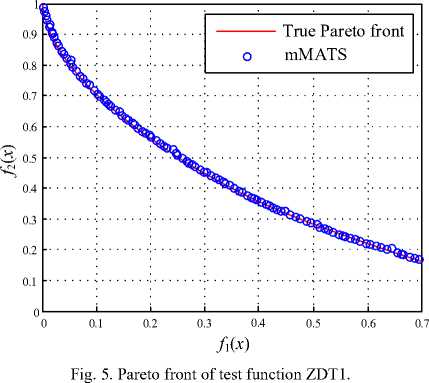
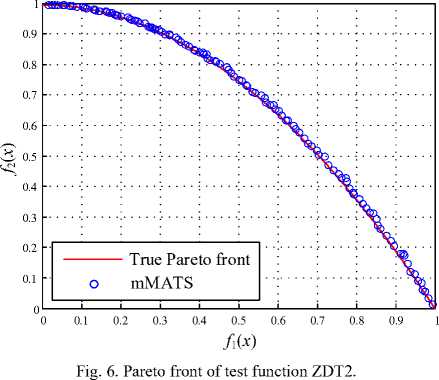
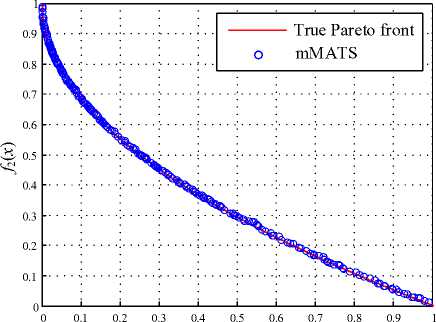
In this work, four widely used multiobjective functions providing a wide range of diverse properties in terms of Pareto front and Pareto optimal set are suggested [40,41]. A set of multiobjective test functions used in this work consists of ZDT1 - ZDT4. ZDT1 is with convex front as stated in (5) where d is the number of dimensions. ZDT2 as stated in (6) is with non-convex front, while ZDT3
fix) = x1, f 2(x) = g(1 — 7f -/ g ), g = 1 +10( d — 1) + ^ d= 2 [x2 — 10cos(4^f,)]
X i e [0,1], i = 1, ^ ,30.
N
E f = | | PFe — PF t || = ^ ( PF e — PF t )2 (9)
j = 1
In evaluation process, the error E f between the estimated Pareto front PF e and its corresponding true front PF t is defined as stated in (9), where N is the number of solution points.
-
B. Search parametric studies
The mMATS algorithm was coded by MATLAB running on Intel Core2 Duo 2.0 GHz 3 Gbytes DDR-RAM computer. Referring to the ATS and MATS algorithms in section II, the search parameters of the ATS consist of number of neighborhood members n , search radius R , BT and AR mechanisms. These parameters are set as the recommendations in [20,21]. For mMATS search parametric studies, a different range of parameters are set to be investigated. For example, the search paths of MATS are varied from 2 – 64 paths. In the DM mechanism, the number of reducing states are varied from 2 – 5 states. As priory results, it was found that the appropriate search parameters for most test functions are MATS with 12 – 20 paths and the DM mechanism with 3 – 4 states.
In these studies, the termination criteria (TC) either uses a given tolerance or a fixed number of iterations. As implementation results, it was found that a fixed number of iterations is not only easy to implement, but also suitable to compare the closeness of Pareto front of test functions. Therefore, for all test functions, a fixed number of iterations of 2000 is set as the TC. The MATS with 15 search paths is performed. The DM mechanism with 3 states: (i) at 500th iteration, reduces 15 to 10 paths, (ii) at 1000th iteration, reduces 10 to 5 paths and (iii) at 1500th iteration, reduces 5 to 1 path, is conducted for all tests.
-
C. Evaluation results
For comparison, the results obtained by the proposed mMATS over all test functions are compared with those obtained by the well-known algorithms, i.e. vector evaluated genetic algorithm (VEGA) [42], nondominated sorting genetic algorithm II (NSGA-II) [43] and differential evolution for multiobjective optimization (DEMO) [44]. The performance of all algorithms is measured via the error E f stated in (9) and for all algorithms, a fixed number of iterations of 2000 is set as the TC. The results obtained from all test functions are summarized in Table 1 – Table 2, and the estimated Pareto fronts and the true front of functions ZDT1 – ZDT4 are depicted in Fig. 5 – Fig. 8, respectively. It was found from all Figures that the mMATS can satisfactory provide the Pareto front very close to the true front of each test function. Referring to Table 1 – Table 2, the mMATS shows superior results in term of error E f to other algorithms with lesser search time consumed.
|
Table 2. Search Time Consumed |
||||
|
Methods |
Search time (secs) |
|||
|
ZDT1 |
ZDT2 |
ZDT3 |
ZDT4 |
|
|
VEGA |
125.45 |
132.18 |
121.40 |
122.24 |
|
NSGA-II |
126.82 |
145.63 |
158.27 |
165.51 |
|
DEMO |
89.31 |
98.44 |
102.32 |
120.86 |
|
mMATS |
65.54 |
72.33 |
82.47 |
78.52 |
0.6
0.8

Table 1. Solution Summary
|
Methods |
Error E f |
|||
|
ZDT1 |
ZDT2 |
ZDT3 |
ZDT4 |
|
|
VEGA |
2.79e-02 |
2.37e-03 |
3.29e-01 |
4.87e-01 |
|
NSGA-II |
3.33e-02 |
7.24e-02 |
1.14e-01 |
3.38e-01 |
|
DEMO |
2.08e-03 |
7.55e-04 |
2.18e-03 |
2.96e-01 |
|
mMATS |
1.24e-03 |
2.52e-04 |
1.07e-03 |
1.02e-01 |
0.4
0.2
-0.2
-0.4
-0.6
-0.8


True Pareto front о mMATS
-
-1 I_________________________I_________________________I_________________________I_________________________I_________________________I_________________________I_________________________I_________________________I_________________________I_________________________I
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
f 1 ( x )
Fig. 7. Pareto front of test function ZDT3.
f 1 ( x )
Fig. 8. Pareto front of test function ZDT4.
-
IV. Bi-Objective Optimal PID Controller Design
In this section, the application of the mMATS to biobjective PID controller design in the automatic voltage regulator (AVR) system is presented. The AVR is commonly used in the generator excitation system of hydro and thermal power plants to regulate generator voltage and control the reactive power flow [45]. The main role of the AVR is to regulate the terminal voltage of a synchronous generator at a specified level. A synchronous generator connecting to power system would critically affect the security of the power system depending on the stability of the AVR. For a simple case, the AVR consists of four main components, i.e. amplifier, exciter, generator, and sensor, respectively. A simplified AVR system controlled by the PIDA controller is represented by the block diagram in Fig. 9, where V e is the error voltage between the reference input voltage V ref and sensor voltage V s , while V u , V r and V f are the controlled, amplified, and excited voltage signals, respectively, and V ( s ) is the output voltage.
Referring to Fig. 9, four main components of the AVR are linearized and modeled by transfer functions as follows [45]. The amplifier model is expressed in (10) by a gain KA and a time constant ta . Typical values of KA are in the range of 10 to 400. The amplifier time constant is very small ranging from 0.02 to 0.1sec. In this work, KA = 10 and a time constant ta = 0.1 sec. are priory set. The exciter model is stated in (11) by a gain KE and a time constant te. Commonly values of KE are in the range of 1 to 400 and the time constant te is from 0.25 to 1.0sec. In this work, KE = 1 and a time constant te = 0.4 sec. are priory assumed. The generator model is linearized and expressed in (12). A gain KG may vary between 0.7 to 1.0, and the time constant tg between 1.0 to 2.0sec. In this work, KG = 1 and a time constant tg = 1 sec. are set as a priory. Finally, the sensor model is a simple first-order transfer function as stated in (13) with a gain KR and the time constant tr ranging from of 0.001 to 0.06sec. In this work, KR = 1 and tr = 0.01 sec. are assumed.
V r ( s ) K A
V u ( s ) 1 + T A s
V f ( s ) KE
V r ( s ) 1 + T e S
V ( s ) K G
V f ( s ) 1 + T G s
V s ( s ) K R
V ( s ) 1 + T r S
Based on the multiobjective optimization context, more than one objective function needs to be performed. In the control application, a step response of the system consists of rise time ( tr ), peak time ( tp ), settling time ( ts ) and maximum percent overshoot ( M p ). Generally, both t p and t s are directly varied according to t r . However, t r and M p are confliction. Once t r decrease, M p will increase and vice versa. Therefore, bi-objective function for designing PID controller of the AVR system by the mMATS in this work is performed as stated in (14), where f 1 ( x ) is the rise time ( tr ) and f 2( x ) is the maximum percent overshoot ( Mp ).
min f (x) = {f1(x), f 2(x)}, f1( x) = tr, f2( x) = Mp,
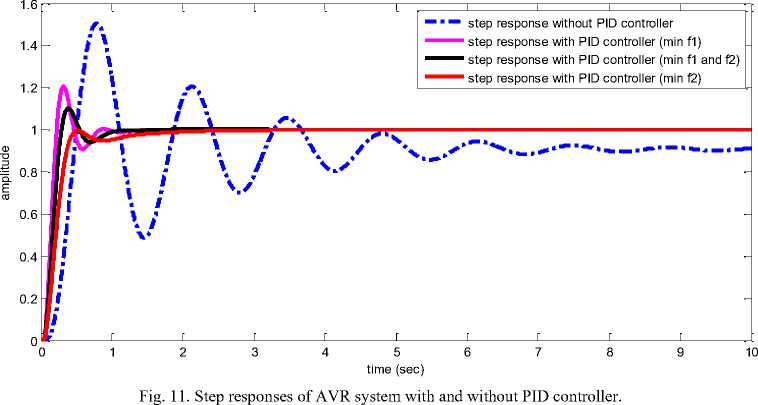
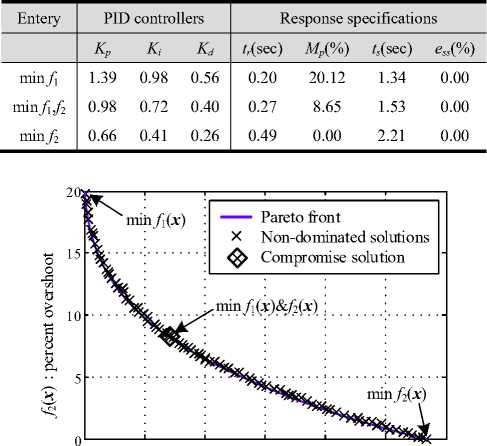
-0 < Kp < 1.5, x = <0 10 < Kd< 1.0 Fig. 9 AVR system with PID controller. According to Fig. 9, the mMATS-based PID controller design is conducted for the AVR system. In this application, the search parameters of the ATS consisting of number of neighborhood members n, search radius R, BT and AR mechanisms are set as the recommendations in [20,21]. For mMATS, the search parameters are performed as the same values in section III. That are the MATS with 15 search paths, the DM mechanism with 3 states: (i) at 500th iteration, reduces 15 to 10 paths, (ii) at 1000th iteration, reduces 10 to 5 paths and (iii) at 1500th iteration, reduces 5 to 1 path and a fixed number of iterations of 2000 is set as the TC. The mMATS algorithm for biobjective optimal PID controller design of the AVR system was coded by MATLAB running on Intel Core2 Duo 2.0 GHz 3 Gbytes DDR-RAM computer. Fig. 10. Pareto front of AVR system design. Table 3. Results of PID design problem by mMATS 0.2 0.25 0.3 0.35 0.4 0.45 0.5 f1(x) : rise time V. Conclusions The multiobjective multipath adaptive tabu search (mMATS) has been proposed to design the optimal PID controller of AVR system based on bi-objective optimization. In TS family, the TS, ATS, MATS and mMATS have been consecutively developed to be one of the most powerful metaheuristic optimization search techniques. In this paper, algorithms of TS, ATS and MATS have been reviewed, whereas algorithms of mMATS have been presented. To perform its effectiveness over multiobjective optimization problems, the mMATS has been evaluated against four standard multiobjective test functions. Results obtained by the mMATS have been compared with those obtained by three well-known algorithms, i.e. VEGA, NSGA-II and DEMO. As results, it was found that the mMAST could provide optimal solutions superior to other algorithms with shortest search time consumed. Moreover, the mMATS has been applied to design an optimal PID controller of the AVR system considered as bi-objective optimization problem. Results obtained shown that the mMATS could effectively design optimal PID controllers of the AVR system. A set of non-dominated (optimal) solutions of the PID design problem are successfully obtained by the proposed mMATS with bi-objective optimization approach. Step responses of the controlled AVR system with PID controllers were very satisfactory.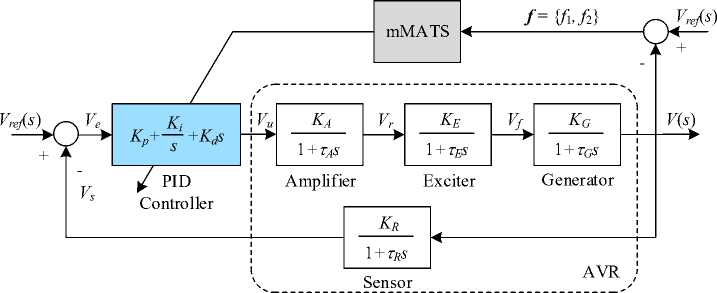
Список литературы Multiobjective Multipath Adaptive Tabu Search for Optimal PID Controller Design
- F. Glover and G. A. Kochenberger, Handbook of Metaheuristics, Kluwer Academic Publishers, Dordrecht, 2003.
- E. G. Talbi, Metaheuristics form Design to Implementation, John Wiley & Sons, Hoboken, 2009.
- D. T. Pham and D. Karaboga, Intelligent Optimisation Techniques, Springer, London, 2000.
- X. S. Yang, Nature-Inspired Metaheuristic Algorithms, Luniver Press, 2010.
- X. S. Yang, “Review of metaheuristics and generalized evolutionary walk algorithm,” Int. J. Bio-Inspired Computation, vol.3(2), 2011, pp.77-84.
- B. Jarraya and A. Bouri, “Metaheuristic optimization backgrounds: a literature review,” Int. J. Contemporary Business Studies, vol.3(12), 2012, pp.31-44.
- F. Glover, “Tabu search - part I,” ORSA Journal on Computing, vol.1(3), 1989. pp.190-206.
- F. Glover, “Tabu search - part ii,” ORSA Journal on Computing, vol.2(1), 1990, pp.4-32.
- R. Battiti and G. Tecchiolli, “The reactive tabu search,” ORSA Journal on Computing, vol.6(2), 1994, pp.126-140.
- N.Wassan, “A reactive tabu search for the vehicle routing problem,” Journal of the Operational Research Society, vol.57(1), 2006, pp.111-116.
- T. Crainic, M. Toulouse, and M. Gendreau, “Toward a taxonomy of parallel Tabu search heuristics,” INFORMS Journal on Computing, vol.9(1), 1997, pp.61-72.
- E. G. Talbi, Z. Hafidi, and J.-M. Geib, “A parallel adaptive Tabu search approach,” Parallel Computing, vol. 24(14), 1998, pp.2003-2019.
- S. M. Sait, H. Youssef, H. R. Barada, and A. Y Ahmad, “Parallel Tabu search algorithm for VLSI standard-cell placement,” in Proc. IEEE International Symposium on Circuits and Systems (ISCAS ’00), 2000, pp.581-584.
- E. Nowicki and C. Smutnicki, “An advanced Tabu search algorithm for the job shop problem,” Journal of Scheduling, vol.8(2), 2005, pp.145-159.
- D. Zhang, Z. Fu, and L. Zhang, “An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems,” Electric Power Systems Research, vol.77(5-6), 2007, pp.685-694.
- F. Glover, “Parametric Tabu-search for mixed integer programs,” Computers and Operations Research, vol.33(9), 2006, pp.2449-2494.
- J. Xu, S. Y. Chiu, and F. Glover, “Probabilistic Tabu search for telecommunications network design,” Journal of Combinatorial Optimization, vol.1(1), 1997, pp.69-94.
- Y. Kochetov and E. Goncharov, “Behavior of a probabilistic tabu search algorithm for the multi stage uncapacitated facility location problem,” in Proc. Operations Research, 2000, pp.65-70.
- D. Ghosh, A Probabilistic Tabu Search Algorithm for the Generalized Minimum Spanning Tree Problem, Idian Institute of Management, Ahmedabad, India, 2003, Working Paper no. 2003-07-02.
- S. Sujitjorn, T. Kulworawanichpong, D. Puangdown-reong, and K.-N. Areerak, Adaptive Tabu Search and Applications in Engineering Design, Frontiers in Artificial Intelligent and Applications, IOS Press, Amsterdam, The Netherlands, 2006.
- D. Puangdownreong, K-N Areerak, A. Srikaew, S. Sujitjorn, and P. Totarong, “System identification via adaptive tabu search,” in Proc. IEEE Int. Conf. on Industrial Technology (ICIT’02), Bangkok, Thailand, vol. 2, 2002, pp.915-920.
- K.-N. Areerak, T. Kulworawanichpong, and S. Sujitjorn, “Moving towards a new era of intelligent protection through digital relaying in power system,” in Knowledge-Based Intelligent Information and Engineering Systems, vol. 3215 of Lecture Notes in Artificial Intelligence, pp. 1255–1261, Springer, New York, NY, USA, 2004.
- D. Puangdownreong and S. Sujitjorn, “Image approach to system identification,” WSEAS Transactions on Systems, vol.5(5), 2006, pp.930-938.
- D. Puangdownreong, K-N. Areerak, K-L. Areerak, T. Kulworawanichpong, and S. Sujitjorn, “Application of adaptive tabu search to system identification,” in Proc. the 24th IASTED Int. Conf. on Modelling, Identification, and Control (MIC2005), Innsbruck, Austria, 2005, pp.178-183.
- D. Puangdownreong and S. Sujitjorn, “Obtaining an optimum PID controller via adaptive tabu search,” Lecture Notes in Computer Science, vol. 4432(2), 2007, pp.747-755.
- C. Thammarat, D. Puangdownreong, P. Sukserm, and S. Suwannarongsri, “Optimum industrial PID controller design for process with time delay via adaptive tabu search,” in Proc. the 29th IASTED Int. Conf. on Modelling, Identification, and Control (MIC2010), Innsbruck, Austria, 2010, pp.197-202.
- N. Sriyingyong and K. Attakitmongcol, “Wavelet-based audio watermarking using adaptive tabu search,” in Proc. the 1st International Symposium on Wireless Pervasive Computing, 2006, pp.1-5.
- D. Puangdownreong, T. Kulworawanichpong, and S. Sujitjorn, “Finite convergence and performance evaluation of adaptive tabu search,” Lecture Notes in Computer Science, Springer-Verlag Heidelberg, vol. 3215, 2004, pp.710-717.
- D. Puangdownreong, S. Sujitjorn, and T. Kulwora-wanichpong, “Convergence analysis of adaptive tabu search,” ScienceAsia Journal of the Science Society of Thailand, vol.30(2), 2004, pp.183-190.
- J. Kluabwang, D. Puangdownreong, and S. Sujitjorn, “Management agent for search algorithms,” in Proc. the 12th WSEAS international conference on Computers, vol. 2(2), 2008, pp.375-382.
- J. Kluabwang, D. Puangdownreong, and S. Sujitjorn, “Management agent for search algorithms with surface optimization applications,” The WSEAS Trans. on Computers, vol.6(7), 2008, pp.791-803.
- D. Puangdownreong, J. Kluabwang, and S. Sujitjorn, “Multipath adaptive tabu search: its convergence and application to identification problem,” Journal of Physical Sciences, vol.7(33), 2012, pp.5288-5296.
- D. Puangdownreong, J. Kluabwang, and S. Sujitjorn, “Application of adaptive tabu search under management agent to control synthesis of scaled vehicle,” in Proc. the 29th IASTED Int. Conf. on Modelling, Identification, and Control (MIC2010), Innsbruck, Austria, 2010, pp.1-6.
- J. Kluabwang, D. Puangdownreong, and S. Sujitjorn, “Multipath adaptive tabu search for a vehicle control problem,” Journal of Applied Mathematics, vol.2012, 2012, pp.1-20.
- S. Sujitjorn, J. Kluabwang, D. Puangdownreong, and N. Sarasiri, “Adaptive tabu search and management agent,” The ECTI Trans. on Electrical Engineering, Electronics, and Communications, vol.7(2), 2009, pp.1-10.
- D-N. Le, “Improving genetic algorithm to solve multi-objectives optimal of upgrading infrastructure in NGWN,” International Journal of Intelligent Systems and Applications (IJISA), vol.5(12), 2013, pp.53-63.
- F. Y. Edgeworth, Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences, C. Kegan Paul and Co., London, 1881.
- V. Pareto, Cours ď économie Politique, Rouge, Lausanne, Switzerland, 1896.
- C. Yunfang, “A general framework for multi-objective optimization immune algorithms,” International Journal of Intelligent Systems and Applications (IJISA), vol.4(6), 2012, pp.1-13.
- E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach,” IEEE Transactions on Evolutionary Computation, vol.(3), 1999, pp.257-271.
- E. Zitzler, K. Deb, and L. Thiele, “Comparison of multiobjective evolutionary algorithms: empirical results,” Evolution Computing, vol.8, 2000, pp.173-195.
- J. D. Schaffer, “Multiple objective optimization with vector evaluated genetic algorithms,” in Proc. the 1st International Conference on Genetic Algorithms, 1985, pp.93-100.
- K. Deb, A. Pratap, S. Agarwal, and T. Mayarivan, “A fast and elitist multiobjective algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol.6, 2002, pp.182-197.
- T. Robicˇ, B. Filipicˇ, “DEMO: differential evolution for multiobjective optimization,” Lecture Notes in Computer Sciences, vol. 3410, 2005, pp.520-533.
- Z. L. Gaing, “A particle swarm optimization approach for optimum design of PID controller in AVR system,” IEEE Transactions on Energy Conversion, vol.19(2), 2004, pp. 384-391.


