Muscle and Baseline Wander Artifact Reduction in ECG Signal Using Efficient RLS Based Adaptive Algorithm

Published Online May 2016 in MECS

In case of emergency and the patient is far from the specialist laboratory, the acquired signal is send to the laboratory for analysis. The analyst properly interprets the data for the correct decision making. During the transmission of the ECG signal, the channel noise is added which is undesired one; it can further degrade the PQRST waveform. During the acquisition of the ECG signal using electrodes which were placed on the body, the ECG signal will undergo numerous artefacts. To carry out the online signal processing, recently a microprocessor based recorders have been developed. Once the ambulance arrived at the site and the patient was taken on board, the ECG monitor was connected to the patient. Using GSM modem with a dedicated antenna, the stored ECG signal in the ambulance system is transmitted to the emergency coordination centre. At the emergency coordination centre the ECG signal could be displayed on the expert station and instructions could be relayed to the ambulance personnel with useful information.

Before diagnosis of the experts for analyzing of the ECG signal report, it is necessary to remove the various noises occur during acquisition of the signal. So filtering of these noises is very important. We know mainly two types of filtering techniques are non adaptive and adaptive filtering. When input signal varies continuously then adaptive filtering technique gives better result compared to non adaptive filtering technique. Various adaptive filtering techniques are developed for reducing of noise in the corrupted ECG signal [1-4]. In [1], Vanalste et al . introduced removal of baseline wander noise and power line frequency from the ECG signal using digital non recursive finite impulse response filters. In [4], Rik Vullings et al. used Kalman filter to enhance the SNR ratio on various ECG signals and at the same time they preserve clinically relevant ECG morphological variations. To acquire the impulse response of a normal QRS complexes and it can be applied for arrhythmia detection in ambulatory ECG recordings with the least mean square(LMS) based adaptive recurrent filter [5]. There are in survey other different techniques are implemented in [6-9] to extract the ECG data information for analysis of the signal.

In [10] Floris et al. proposed prediction of respiratory motion signals using different versions of LMS and normalized LMS algorithms. The baseline wander noise drift can be corrected by using bionic wavelet transform, proposed Sayadi et al. in [11]. In [12] Samit et al. proposed, Stockwell transform(S-transform) to reduce the noises like Muscle Artifacts (MA), Electrode Motion (EM) and Baseline Wander (BW) in the ECG signal during acquisition and transmission; but leads to less improvement in Signal to noise ratio. In many practical situations output is in nonlinear form, to bring this nonlinear into linear form in [13], they proposed adaptive inverse model of nonlinear systems. In this paper they used the second order Volterra filters and FLANN filters used to lower mean square error.

Aboulnasr’s algorithm [14] gives improvement over Kwong’s Algorithm, but reduction of the step-size value too early in some situations and leads to lag (1) error autocorrelation function. This results a slow convergence rate in Aboulnasr’s algorithm. To improve the convergence rate at initial stages and to reduce the misadjustment ratio at later stages, recently, Gowri et al. [15] proposed an efficient variable step size LMS algorithm. To avoid the misdiagnoses on the part of the heart patient, an intelligent system had been developed based on neural networks in [16], which can describes the diagnose of heart diseases if any kind of disorders. The various non adaptive (FIR filters like Kaiser window techniques, IIR filters like Butterworth) and adaptive (LMS and NLMS) filters are used in [17], to remove PLI and BW noise in the ECG signal. But by using this LMS and NLMS algorithms the convergence rate is slow compared to RLS algorithm.

For minimum computational complexity and better performance of various noise cancellation in ECG signal are developed in Rahaman et al. in [18] . In [19] Butt et al. proposed cancelling of power line interference noise in ECG signal using state space recursive least square (SS-RLS) adaptive filter with the estimated frequency from the Discrete Fourier Transform.

In RLS adaptive algorithm the error reduces by means of weighted sum of least squared criteria, but in LMS the error minimizes in the form of weighted mean squared criteria, due to this the RLS algorithms removes error more compared to LMS algorithm with somehow additional complexity. Unlike to RLS algorithm, it does not depend upon any step size parameter. The RLS algorithms gives fast convergence rate and high signal to noise ratio than the LMS based adaptive algorithms such as Variable step size LMS, Normalized LMS, Block based LMS and Sign based LMS algorithms.

To enhance the ECG signal quality, we introduced in this paper block based error normalized RLS (BB-ENRLS) algorithm, sign block based ENRLS (SBB-ENRLS) algorithms which are derived from basic RLS algorithm. These algorithms are used in this paper for reducing of Muscle artefact noise in the corrupted ECG signal. The simulation result shows that Block based ENRLS algorithm gives higher convergence rate and high signal to noise compared to basic LMS algorithm.

The rest of the paper is organized as follows. In section 2, adaptive filtering techniques are used to enhance the ECG signal quality. In section 3, Simulation results presented. Finally Section 4 presents conclusion of the topic.

• II.    A daptive F iltering T echniques for E nhance T he ECG S ignal Q uality

There are many adaptive filtering techniques are there, but for eliminating of noise in the corrupted signal the general adaptive filter structure is shown in Fig. 1. From the figure desired signal d(p) plus artefact is given as one input and reference signal is given as another input x(p). By using adaptive filter algorithm the weight updating changes according to the input signal until for minimizing of the error signal e(p).

The LMS algorithm is widely used because of its simplicity, its weight update equation is given as

W ( p + 1) = W ( p ) + M e ( p ) X ( p ).   (1)

Where W ( p ) is the weight updating at p ^th index. W ( p ) = [ W )( p ) W i( p ) ... w M - 1 ( p )] ^r          and

X ( p ) = [ x ( p ) x ( p — 1) ... x ( p — M + 1)], are weight vector and reference input for the filter length M. The output error can be analyzed as e ( p ) = d ( p ) — y ( p ).

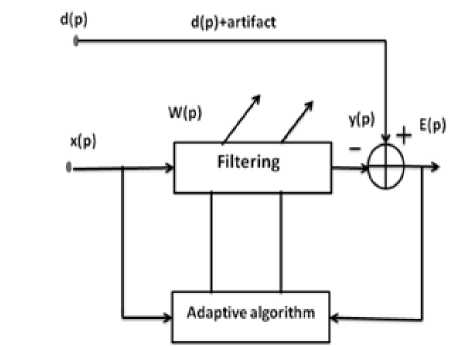
Fig.1. Adaptive filter structure

In the LMS algorithm the weight vector mainly depends on the chosen best value of the step size and also the cost function depends on the square of the error. But in RLS algorithm the cost function changes with respect to the least square manner, and it does not depends any step size parameter. When input signal is non stationary then RLS algorithm gives better elimination of noise compared to LMS algorithm.

The cost function for RLS algorithm is

J ( p ) = 1 X^{p —} i\ e ( i )2|.               (2)

i = 0

For eliminating of better noise removal X is chosen nearer to be one, it is called exponential factor. The complete weight vector for the RLS algorithm is given as

W ( p ) = X P ( p ) Rdx ( p — 1) + d ( p ) P ( p ) X ( p )   ₍₃₎

Where P ( q ) indicates inverse of auto correlation of input is signal, it can be initialized with 5 ¹ 1 and R dx is the deterministic cross correlation between the desired signal and the input vector. The value of 5 to be chosen as small less than one and I indicates identity matrix chosen as length of filter order.

The simplified weight updating equation for Recursive Least Square coefficient can be written as

W ( p ) = W ( p - 1) + e1( p ) g ( p ).      (4)

Where g(p)the gain vector and priori error is can be denoted as e1( p) = d (p) - WT (p-1) X (p).     (5)

Normalization of the algorithm gives fast convergence [20] compared to normal algorithms. For this normalization if we include block based then evaluation time is reduced. So we applied these two techniques to RLS algorithm called as BBENRLS algorithm its weight updating equation is given as

W ( p ) = W ( p - 1) + - e M" g ( p )     (6)

b ^{+ e1} Mi

Where el Mi = max{| el k\, к e Zi} Z =

{iM , iM + 1, ..., iM + M - 1}, i e Z .

In (6) if e 1 Mi Ф 0 then we consider b =0. If £ 1 Li = 0 then b =1 is chosen then equation (6) reduces to equation (3).

The computational complexity can be reduced by using sign function to the above derived function called as Sign Block based ENRLS algorithm. The weight update equation for Sign BBENRLS algorithm (SBBENRLS) is given mathematically as

SGN ( e 1( p ))

^{W (} p ) = W ⁽ p ^{- 1) +} —---2"^ g ⁽ p )   (7)

^{b + e1} Mi

Where ‘SGN’ is known signum function and it is defined as

1: e1( p ) >  0

sgn{ e 1( p )} = <   0: e1( p ) = 0

_- 1:  e1( p ) <  0

Due to this sign function number of multiplications is reduced compared to BBENRLS algorithm, but SNR ratio is somehow reduced compared to RLS algorithm.

• III.    S imulation R esults

  The simulation result is carried out by taking original ECG signal from MIT-BIH [21] physionet database. In this arrhythmia database there are totally 48 half hour excerpts of of two channel ambulatory ECG recordings, which were obtained from 47 subjects, women aged 2389 years including 25 and men aged 32-89 years. From this data base we collected six data records randomly; those data’s are 100, 102, 104, 111, 207 and 210. The records are sampled at the rate of 360 Hz with a resolution of 10 mV range. For comparison of derived adaptive filters, we measured Signal to noise ratio (SNR) and analyzed with LMS algorithm. The number of samples are taken on x-axis and amplitude is taken on y-axis for the all figures.

The main sources of noises which are degrade the performance of ECG signal are shown in Fig.2. In the Fig.2(a) is a 60Hz Powrline Interference (PLI) noise, which is non physiological noise, while using measuring instrument to acquire the ECG signal from person this PLI noise is automatically added into the signal. Fig.2(b-c) are physiological noises: Baseline Wander (BW) noise is a very low frequency noise due to respiration problem and Muscle Arifact (MA) noise is very high frequency noise compared to all other noises which is also degrade the ECG signal.

Fig.2(d) is Electrode Motion (EM) noise which is mainly due to motion of electrode contact to the person. In this paper we considered MA and EM artifacts, which are adds to the pure ECG signal, for analyzing of adaptive filter characteristics.

While measuring the ECG signal from the heart function of the body, the person is in tension, then frequency of the signal increases, when compared with normal ECG frequency range. This increasing frequency may sometimes fully corrupt the original information of the ECG signal, this interference is called Muscle artifact (MA) noise. The real MA noise is collected from the physionet noise stress database. The MA noise and additional random noise are added to the original ECG signal and given as input signal to Fig. 1. The random noise of 0.001 is added, because in some times when data is transmitted for diagnosis purpose then channel noise is added to pure signal which may degrade the signal quality. Muscle artifact interference appears as continuous variations, which vary faster than ECG waves. As shown in Fig. 3(a) and Fig. 4(a), MA corrupted with pure ECG signal of record number 102 and 210. This MA noise is eliminated using different derived adaptive algorithms as shown in Fig. 3(b-e) and Fig. 4(b-e). From these figures we observed that sign based algorithm has some residue of noise compared to other algorithms.

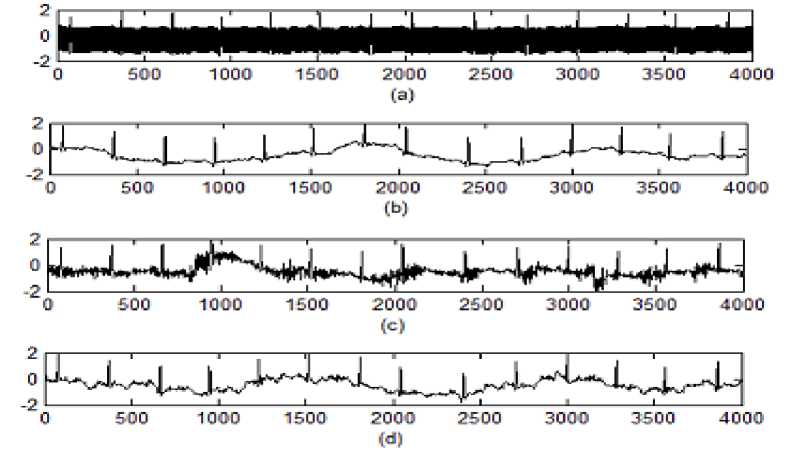
Fig.2. (a) Pure ECG signal corrupted with (a) Power Line Interference (PLI) (b) Base Line Wander (BW) (c) Muscle Artifact (MA) (d)Electrode Motion (EM).

2 0 -2 2 0 -2 2 0 -2 2 0 -2 2 0 -2	y^i^y-^^^        * V'M^ijurf-^^             |l^#vJy<^^          —JA/*' -^^jilN)^^
	D	500  1000  1500	2000	2500  3000 (a)	3500	4000	4500	5000
	кф|<**Нч-Ч13^^         якА^*--^\/^Ц«ДА--^-Ц^'^'Ч-тЛ^.-"--Jk^H-—.„ , ^*4^ J-^ar^H^J-^ , ^A^— -w
	D	500  1000  1500	2000	2500  3000 (b)	3500	4000	4500	5000
	k^	- A^ ^^А/'^аАг ^ A " - A_—-	v —	-\Г ~ -\.------^		A~ --A"	-A/ — -A
	D L,^^ 3	500  1000  1500 i.U,r^^Vp‘>. „..^^ ^M—rW^.lf-^--    Лу -~^„J C _„___ 500  1000  1500	2000 2000	2500  3000 (c) -^" —Uy——1^--— -\ 2500  3000 (d)	3500 3500	4000  4500 A—- .^^Ji^   Д^ ~   ^ 4000  4500		5000 5000
					r— ^aL -^-iwk—-—-Ак,/*" ^^"\^ribuumJ,|^^~ "—
	D	500  1000  1500	2000	2500  3000	3500	4000	4500	5000

(e)

n

BBENRLS algorithm (e) BBENRLS algorithm.

2 0 -2	A^AL.™ -А^у-^^^А ^^АА^^д^^^^^             Ai^h~ А^»^ A__^^^ Л,^^^!^^ '-*■									—^ itwz^H^kn^^^  ™
	D	500	1000	1500	2000	2500	3000	3500	4000	4500	5000
						(a)
2 0		L		n        L h	L		L		u	L
-2	D	500	1000	1500	2000	2500	3000	3500	4000	4500	5000
						(b)
2 0					4		'-	n     Л n		u
-2	D	500	1000	1500	2000	2500	3000	3500	4000	4500	5000
						(c)
0 2 -2	t-Lunr J	^«- 'Л^ «уNtr^JU^^, Л^™Л - -		-Л С.л....	Л „-zi..			Л_ Х..Л„	-V'.......^	-iA_^	л_-
	D	500	1000	1500	2000	2500	3000	3500	4000	4500	5000
						(d)
2 0		L		L	L		L	r                               г	L	L
-2	3	500	1000	1500	2000	2500	3000	3500	4000	4500	5000

(e)

Fig.4. (Rec. No. 210) (a) ECG signal corrupted with muscle artifact. Removal of MA noise using: (b) LMS algorithm (c) RLS algorithm (d)Sign BBENRLS algorithm (e) BBENRLS algorithm.

As shown in Table 1., indicates performance evaluation calculation in terms of Signal to Noise Ratio, for the reduction of MA artifact from the corrupted ECG signal using different adaptive algorithms. We calculated SNR values for different records and then averaged this values. From the average analysis, the average SNR for BBEN-RLS give high value of 7.7363 dB and next place is RLS algorithm has average SNR of 6.1121 dB. So comparing to LMS adaptive algorithm, the RLS based algorithm gives high removal of noise.

Table 1. Performance measure of the different adaptive filters for reducing of MA noise in ECG signal in terms of Signal to noise ratio in dB.

Noise	Rec. No.	SNR After Filtering
		LMS	RLS	SBB ENRLS	BB ENRLS
MA	100	3.7932	5.552	3.2222	7.8484
	102	4.2769	6.3396	4.2098	7.9085
	104	4.3567	5.3116	4.7321	7.2029
	111	5.2968	6.753	4.3182	8.2682
	207	4.2137	5.2577	5.0707	8.2533
	210	5.0329	7.4588	4.3099	6.9365
	Avg	4.4950	6.1121	4.3104	7.7363

As shown in Table 2., the mean square error (MSE) value of different algorithms for the elimination of MA. We calculated MSE for different records and calculated average value. LMS algorithm gets 0.0149, RLS algorithm gets 0.0048 and SBBENRLS algorithm gets

0.0132.From the average calculation analysis the BBEN-RLS algorithm gives reduced MSE value of 0.0034 at the end of the iteration samples compared to other algorithms. The sign based RLS algorithm may chosen to reduce the computational complexity of the processor design and also for fast evaluation of the signal.

Table 2. Mean Square Error values for different adaptive algorithms for the reduction of MA.

Noise	Rec. No.	MSE After Filtering
		LMS	RLS	SBB ENRLS	BB ENRLS
MA	100	0.0224	0.0103	0.0304	0.0027
	102	0.0113	0.0043	0.0128	0.0021
	104	0.0150	0.0039	0.0130	0.0073
	111	0.0070	0.0020	0.0093	0.0014
	207	0.0274	0.0060	0.0051	0.0025
	210	0.0066	0.0023	0.0087	0.0049
	Avg	0.0149	0.0048	0.0132	0.0034

The real BW noise is collected from the physionet noise stress anthemia database. The BW noise and additional random noise are added to the original ECG signal and given as input signal to Fig. 1. The BW noise is given as reference input. The random noise of 0.001 is added, because in some situations when data is transmitted for specialist help to diagnosis then channel noise is added to pure signal, which may corrupt the signal quality.

2 0 э 500 1000 1500 2000 2500 (a) 3000 3500 4000 4500 5000 2 - 1 0 -2 г 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 (b) 2 0 г -2 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 (c) 2 - 1 0 -2 Г 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 (d) 2 0 - Ду, -2 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 (e) a go      e            a go     .

n

02							—€_L
	D	500	1000	1500	2000	2500  3000 (a)	3500	4000	4500	5000
2		1-		L .		к           к            u
0
		г	Г	Г		г                  г			г
-2
0		500	1000	1500	2000	2500  3000	3500	4000	4500	5000
						(b)
2
0					11              Д               1
-2		Г	Г	Г	Г	Г                  Г	Г	Г	Г
0		500	1000	1500	2000	2500  3000	3500	4000	4500	5000
						(c)
02										---.—-
-2
0		500	1000	1500	2000	2500  3000	3500	4000	4500	5000
						(d)
2
0			_ д.___ „_______Л		-L ^Д^^и
		г	г	г	г	г                г	г	г	г
-2
0		500	1000	1500	2000	2500  3000	3500	4000	4500	5000
						(e)

Fig.6. (Rec. No. 210) (a) ECG signal corrupted with Baseline Wander. Removal of BW noise using: (b) EMS algorithm (c) RES algorithm (d)Sign a go      e            a go     .

-5

-55

LMS sign BBENRLS RLS

-10

-15

-20

-25

-30

-35

-40

-45

-50

2000  2500  3000

Iterations

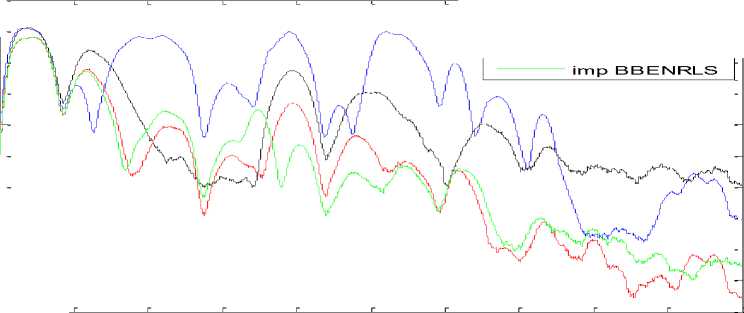
Fig.7. (Rec. No. 210):Excess Mean Square Error Convergence characteristics

Baseline wander interference appears as continuous variations, which vary slowly than ECG waves. Due to this low frequency noise the origin of the baseline is changed. As shown in Fig. 5(a) and Fig. 6(a), BW corrupted with pure ECG signal of record number 104 and 210. This BW noise is reduced using different derived adaptive algorithms as shown in Fig. 5(b-e) and Fig. 6(b-e). From these figures we observed that sign based algorithm has some residue of noise is still there compared to other algorithms.

As shown in Table 3, performance evaluation calculation in terms of Signal to Noise Ratio using different adaptive algorithms, for the reduction of BW artifact from the corrupted ECG signal. We measured SNR values for six different records and then averaged these values.

Table 3. Performance measure of the different adaptive filters for reducing of BW noise in ECG signal in terms of Signal to noise ratio in dB.

Noise	Rec. No.	SNR After Filtering
		LMS	RLS	SBB ENRLS	BB ENRLS
BW	100	3.4178	5.5988	5.2517	6.6461
	102	4.7552	6.1563	5.9839	6.9654
	104	4.4898	6.4376	7.7345	7.9697
	111	5.1621	6.6634	5.9841	7.4378
	207	5.0165	7.3278	6.8176	8.3711
	210	5.9342	7.5679	7.3618	9.5699
	Avg	4.7959	7.5679	6.5222	7.8266

From the averaged analysis, the average SNR for BBENRLS give high value of 7.8266 dB and next place is RLS algorithm has average SNR of 7.5679 dB and SBBENRLS gets 6.5222 dB. So comparing to LMS adaptive algorithm, the RLS based algorithm gives high removal of noise and also fast convergence rate.

Table 4. Mean Square Error values for different adaptive algorithms for the reduction of BW.

Noise	Rec. No.	MSE After Filtering
		LMS	RLS	SBB ENRLS	BB ENRLS
BW	100	0.0263	0.0058	0.0106	0.0058
	102	0.0089	0.0043	0.0049	0.0028
	104	0.0148	0.0029	0.0035	0.0028
	111	0.0046	0.0013	0.0026	0.0012
	207	0.0198	0.0025	0.0031	0.0029
	210	0.0050	0.0011	0.0024	0.0014
	Avg	0.0132	0.0029	0.0045	0.0028

From the Table 4, it shows that MSE values for reduction of BW noise, using different adaptive algorithms. We calculated MSE values for six records and averaged, from the average MSE values, BBENRLS algorithms gets 0.0028, RLS algorithms gets 0.0029, SBBENRLS algorithm gets 0.0045 and LMS algorithms gets 0.0132. So comparing with LMS based, BBENRLS gets less MSE, and also fast convergence rate. Fig.7 shows the Excess mean square error of different adaptive algorithms for reduction of MA noise for the data record number 210. It is observed from the figure the EMSE is less for BBENLMS algorithm compare with other algorithms.

• IV.    C onclusion

In this paper we reduced Muscle artifact noise and Electrode motion noise in the corrupted ECG signal. For reducing of this noises we derived block based Error normalized RLS algorithm and sign Block based error normalized RLS algorithm, from the RLS algorithm. From the derived algorithms the BBENRLS algorithm reduces the MA and BW noise, as high as compared to RLS and LMS algorithms. Based on the comparison of SNR values and MSE from the simulation result, the derived BB-ENRLS algorithm gives better reduction of noise than other algorithms, and it is also far beast when compared with LMS algorithm. For processor design less computational complexity is preferred then Sign BBENRLS algorithm is best.