N-кратное расщепление явной разностной схемы для уравнения вихря в вязкой несжимаемой жидкости

Пастухов Ю.Ф. под лицензией CC BY 4.0. Чтобы просмотреть копию этой лицензии, посетите

Рассматривается гидродинамическая задача для вязкой несжимаемой жидкости в прямоугольной каверне с подвижной крышкой. Данная тестовая задача является полигоном для апробации новых вычислительных методов и алгоритмов, так как имеет в прямоугольной области две особые точки поля скорости [1], [2], [3]. При движении точки наблюдения по левой боковой стороне прямоугольника вверх в угол значение скорости равно нулю. Справа от угла на верхнем отрезке скорость скачком меняется с нуля до единицы и направлена вместе с крышкой вправо. Аналогичная ситуация происходит в верхнем правом углу. В работе предложен алгоритм n -кратного расщепления явной разностной схемы для уравнения вихря.

В работе Р.П. Федоренко описан [4, с. 137] метод расщепления уравнения в частных производных по физическим направлениям (разделение по слагаемым в общем уравнении). В методе расщепления на каждом дробном временном интервале т 1 = т ₀ / n использовалось одно и то же уравнение вихря в общем виде, а число дробных шагов (кратность расщепления) было не n =2-3 как в работе [4], а n =100, 200.

Постановка задачи

Рассмотрим классическую гидродинамическую задачу в прямоугольной области (каверне) с системой уравнений в частных производных, начальными и краевыми условиями для физических полей [1].

Обозначим ( u ( x , y ), v ( x , y )) вектор скорости жидкой частицы (на твердой границе – боковых отрезках и на нижнем отрезке прямоугольной каверны скорость равна нулю – условие прилипания частиц жидкости). Также нормальная компонента скорости равна нулю на всей прямоугольной границе. Начало системы координат расположим в нижнем левом углу прямоугольника, направим ось у-вверх, ось х-вправо. Ширину прямоугольной каверны обозначим L, высоту буквой H.

В гидродинамической задаче в закрытой каверне подвижная верхняя крышка перемещается вправо с постоянной скоростью u _max характерные масштабы длины L , времени L

, скорости umax, функции тока Lumax, max вихря "ax , числа Рейнольдса Re . Введем без-L размерные переменные: x – горизонтальная координата, у - вертикальная координата, щ, w – безразмерные функции тока и вихря соответственно, (u, v) - вектор безразмерной скорости, t – безразмерное время по формулам

0 < x = Х < 1, 0 < у = У < k = H Щ = — Щmax = Lumax L           L     L     Wmax uvw u =----, V =----w =----, wmax max      max      max umax

L

t = - , T = — ,Re = u ma L

^T     u max         ^V

С безразмерными переменными и функциями запишем систему уравнений гидродинамики [1], [2]:

W xx + W yy = - w ( ^x , y ), ⁰ <  x = x <  1, 0 <  y <  k _max w = v x - u y ,

<

u = w y ; v = ^—w x ,

-  - -  - -    1 /-   - v  - wt + u • Wx + v • Wy = — wxx + wyy 10 < t =—

Re V         'T

W = 0, v  = 0, u  = 0, u=

I г          Г           1 ^           I r \ г.

• (1)

Здесь Г 1 - объединение боковых сторон и нижнего отрезка, Г\Г 1 - верхний отрезок прямоугольника Г. Первым в системе (1) следует уравнение Пуассона для неизвестной функции тока и известной функции вихря. Двумерное уравнение Пуассона на прямоугольнике решается в матричном виде за конечное число арифметических действий с четвертым или шестым порядком погрешности [5, 6]. Далее мы опустим черту сверху над безразмерными функциями, временем и координатами.

Вторая строка системы (1) - функция вихря вычисляется через координатные производные поля скорости. Третья строка - компоненты скорости - вычисляются как частные производные от функции тока. Четвертая строка - уравнение динамики вихря, которое в системе уравнений (1) единственно явно зависит от времени. Слева стоит полная (конвективная) производная по времени. На границе прямоугольника отсутствует вертикальная компонента скорости, а горизонтальная равна нулю на нижнем отрезке и боковых сторонах, а на верхнем отрезке она равна единице.

Кроме двух упомянутых особых точек поля скорости для тестирования алгоритма использовалось сильно нестационарное и завихренное начальное поле скоростей. Оно задавалось нами [2] на равномерной прямоугольной сетке по формуле (2):

u ( x n , y m ) = ^- u 0 ⁽ x n ) f y m 1 ^sin f ^T- \

I k J ^ 2 k J

1        k

\ x n = ⁿh 1 , y m = mh 2 , ^h 1 = —, ^h 2 =— , n 1         n 2

n = 0, n , m = 0, n ₂, n = n₂ = 100

где профиль (3) горизонтальной компоненты скорости на верхнем отрезке каверны

( y = ^k = 1 ) имел вид симметричной трапеции [2] без особых точек поля скорости:

	x n            n„     1 — ,0 <  x <  t , t = — = — т             п  20
u ( x , k ) = u 0( x ) = ^	1, T <  x <  1 — T , 1 — x ,            , -----,1 — T <  x <  1, T	(3)

Аналитически метод n-кратного расщепления уравнения вихря внутри одного временного интервала можно записать в виде k+((/+1)/n)       k+(i / n)

W       — W       A

---------------+ u

T / n k+(i / n)      k k+(i / n) = xy

= ^ ( ⁿ ) + w j ^ i / ⁿ ) ) , i = 0, n — 1 •        (4)

Система рекуррентных уравнений (4) для вихря с замороженным полем скорости (uk (x,y),vk (x,y)) состоит из n дробных шагов i = 0, n — 1, верхний индекс i - указывает дробный слой времени в (4), индекс к - номер целого слоя времени в уравнении вихря в системе (1). Поля скорости, функции тока меняются последовательно, согласно системе (1), в которой поле вихря имеет уже не дробные индексы wk+i /n, а целые wk . В цикле с системой уравнений (4) изменяется только поле вихря wk+i /n, i = 0, n—1. Поле скорости скачком изме- няется, когда переменная внешнего цикла увеличивается на единицу от k до k+1в системе уравнений (1).

Идея решения системы уравнений (4) заключается в уменьшении накопления ошибки округления и времени вычислений. Дифференциальные операторы по координате в (4) аппроксимированы, как и все уравнения системы (1), а также граничные условия с точностью O ( h ⁴ ) , а по времени с точностью O ( т ) •

Предположим, что система уравнений (1) спектрально устойчива с максимальным временным шагом равным т , а система уравнений (4)

с максимальным временным шагом т ₀ / n .

Таким образом, за время т ₀ / n , решая n раз уравнение (4), мы получаем уже скачок по времени т ₀ (в n раз больший, чем последовательное решение системы уравнений (1)) и уменьшаем ошибку округления, так как внутри цикла системы (4) не решаем другие уравнения системы (1).

Второе важное преимущество схемы n-кратного расщепления уравнения вихря (4) заключается в достижении установившихся конечных полей скорости, вихря и функции тока (15 значащих цифр в каждой точке поля не меняются во времени после 21000 итераций).

Уравнение (4) линейно относительно координатных производных w ix , w iy , w Xx , w yy . Ап-

-1- 1 - 5 w ₀ + ⁴ ( w + w J-—( w + w ₂) | = w (0) - —h⁴ w ⁽⁶⁾ ( & ), (10)

2 1        0   3^1     ^—1'    12    2      -2 J ХХ^ ' 9Q Х \^l>> \

& &  е ( - 2 h ,2 h ) .

Таким образом, для уравнения вихря в системе уравнений (1) во внутренних узлах с учетом формул (9), (10) можно найти невязку (11) на временном слое k с шагом т ₀ :

проксимируя каждую производную с порядком O ( h ⁴) , получим невязку уравнения (4) по координате с той же точностью. Для первой производной на симметричном шаблоне методом неопределенных коэффициентов [5], [6] имеем

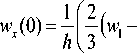
w - 1 )-^ ( w 2 —

w _{- 2} ) | + 0 ( h ⁴) •

Получим аналогичную формулу для второй производной на симметричном шаблоне [5], [6]:

wk + — wk + u^k • \w_x (0) - — h⁴w ⁽⁵⁾ ( & ) | + t               tt                  x                         x       1

+ v^k • | w (0) - — h ⁴ w (⁵⁾ ( & ) | = — M + w^k - y      30      y 2     Re xx    yy

- h 4 ( w X ^6,fe) + w У ‘’(^ J &"^^ & ^e ( - 2 h ,2 h ) o R = 1 0 w k - ^ h⁴ (u k w? & 1 ) + v k w У ⁵’ ( & 2 ) )+

1 ( w Д0) = h21   2

+ ⁴ (

^w 1 + ^w - 1

^)-^⁽ w 2 ⁺ w - 2 ) l ^{+ 0 ( h 4}) • ⁽⁶⁾

+ B h T ( wX⁶⁾ & 3 ) + wУ⁶ ’ & 4 ) ) = 0 1 0 + h ⁴) •  (11)

90 Re

Формулы (5), (6), можно использовать на

внутренних узлах, удаленных от сторон прямоугольника не менее чем на два координатных шага сетки.

На первом прямоугольном контуре с уз-

лами, удаленными на один шаг от сторон пря-

моугольника, получим первую производную

(методом м. н. к.) на шаблоне со смещенным

центром [5], [6] (индекс -1 имеет узлы сетки на

границе прямоугольника):

w x ⁽⁰⁾ = 7^|- h V

1 w

4   ^{- 1}

- -w + - w, 6⁰2¹

- 1 w 2 + £ W 3 1+ 0 ( h ⁴) • (7)

Аналогично, для второй производной получим формулу (8) на шаблоне со смещенным центром (узел с нулевым индексом расположен на первом прямоугольном контуре, а узел с индексом -1 расположен на границе прямоугольника). Назовем прямоугольник и узлы на нем нулевым прямоугольным контуром [5], [6], [1], [2].

®  1 ( 5

w xx ⁽⁰⁾ =7Г| 7 ^w - 1 h V 6

- - w n - - w + ^_ w? 4 ⁰ 3 ¹ 6 ²

- 1 w ₃ + ^ w 4 1 + 0 ( h ⁴ b)

Порядок аппроксимации невязки R = 0 1 + h ⁴) сохраняется и на первом прямоугольном контуре согласно формулам (7) и (8).

Рассмотрим спектральную устойчивость разностного уравнения вихря в системе (1) в пределе при быстром движении жидкости (число Рейнольдса Re = 1000 ) и при медленном вязком течении, например, движении крови в капиллярах Re ^ 0 )[7]. Приведем определение спектральной устойчивости из работы [6, с. 125].

Определение [6], [4] . Если при заданном законе стремлении т , h ^ 0 существует постоянная 0 <  с <» , такая, что для всех q , w е [0,2 ^ ] справедливо неравенство | 2 ( q , w ) < exp( ст ) , то спектральный признак выполнен.

В первом случае в (1) при Re ^» пренебрежем диффузией в уравнении вихря. Тогда с центральным шаблоном на внутренних узлах сетки запишем разностное уравнение переноса в системе уравнений (1):

Разложив формулы (5), (6) в ряд Тейлора на центральном шаблоне, получим невязку (центр шаблона с координатой х=0):

-----— + uk • wk + vk • wk = 0, Zj =10 о т0              x         y       1 h wm+1- wm,n+z 1 um,nlxwm,n+vm,nlyw,n)=0, (12)

121     1

—I — ^{( w} 1 ^{- w} - 1 ^)--^{( w} 2 ^{- w} - 2 ) | = ^w x ^(0)-— ^{h w} Х Ш ⁽⁹⁾ h V 3             12            I           30

l

k x m,n

2 k

3 ⁽ w m , n + 1

—

w m , n - 1 )  |2 ⁽ w m , n + 2

^- w m , n - 2 )

^k ym

2 k

3 \   m + 1, n

- w m - 1, n ) — у ( w m + 2, n - w m - 2, n ) •

f _2m ax = max — ^f 4 - V 1 - x ^{2 А}

^2max    x e [0,1] 3 К              J

= 3,

Подставляя в уравнение (12) функцию

^f max = max ^f max ,

f ' = f m •

возмущения [4]   w m , n = 4 ( p , y )exp ( i ( n p + m y ) )

i = V- 1, p , y e [0,2 ^ ]   получим спектральное

уравнение (13):

Тогда из (13) получим абсолютное значение:

1 4 = J1+ z 2 U m , n f ( p ) + v mj ( у V < Y z 2 4( f J - 1 + 2 f^Z =

(Л 4      1            4

⁴ = ^{1 + iz} 1 l u J tM p ) ^- уМЛ) 1 + v m , n l T^sin ( y ) ^- -sm( V ) II •

К К 3        6        j к 3        6        Л

= 1 + 2 f ^_axz 2 = 1 + 2 f ^_ax| -° I = 1 + т I 2 f _n ² _{a x}4

max 1          max               0    max

К h J          К        h

•

Рассмотрим задачу на максимум:

f ( p ) =

— sm⁽ p ) -- sm⁽² p )

^ max p e [0,2 n ] , (14)

Сравнивая последнее выражение с определением спектрального признака устойчивости получим [5], [6] постоянную c

^{f (} p ) = ^y^ I^{4 -} cos n = ^y^j⁴ ± 7^{1 - s}in ^{2 (} p )| < ⁵

Обозначив x = |sin( p )|, x e [0,1] , перейдем

к задаче

f ( x ) =

^ max x e [0,1] :

1 4 <  exp ( с т 0 ) - 1 + с т 0 о c = 2 f max T 2 = const о T 2 = const .

При медленном вязком течении [7] Re ^ 0 можно пренебречь конвективным переносом, но сохранить слагаемое с диффузией вихря.

Разностная схема для уравнения вихря в

(1) на внутренних узлах сетки примет вид

a) запишем необходимое условие экстремума:

w

к + 1

—

w

k

f ( x ) =

^ max ^ f ( x ) = 0

^т 0

= i ⁽ w x ⁺ w y ) ^z 2 =

Jg Re h ^2,

c

f (x ) = 1 4 + Я 3

—

x ²

+ x

к

4^1 - x ²+ 1 - 2 x²

^f - 2 x Y

К 2VYY ^J J

= 0 о

1 \   ²

= 0 ^ 4 x ⁴ + 12 x ² - 15 = 0 ^

₂   - 3 + V24

x =-------

w ^{+ 1} = w + z 2.⁵ w m , n +- ⁽ w m , n + 1 + w m , n - 1 ^)——⁽ w m , n + 2 + w m , n - 2 ) +

+ ( w «l » + w k -l J( w 'X »+ w k -2 я) | •  (15)

у m + 1, n       m 1, n /            m + 2, n       m 2, n \       '

Подставим в разностную схему (15)

функцию возмущения вида [4]:

w mn , n = 4 ( p , y ) exp ( i ( n p + m y ) ), i = V-1, p , y e [0,2 n ]

f im _и = max x ^f 4 + V 1 - x ²1 = x ^f 4 + J 1 - x²

^{J 1ma} x    x e [0,1] 3 К              J 3 К

x =J Л 6—

получим

спектральное

уравнение^

6 —

f 4 Л Д

V 2

к

—

А

Тб   - 1,37222 ;

J

b) во втором случае

f ( x ) =

^ max ^ f ( x ) = 0

c

f(xx ) = 3 4 - *

—

x ²

- x

(       81,

4 = 1 + z ₂1 - 5 + -(cos( p ) + cos y )) —(cos(2 p ) + cos(2 y )) I , (16) К 3                   6                    J

Введем вспомогательные переменные: x = cos( p ), y = cos ( y ), x , y e [ - 1,1], cos (2 p ) = - 1 + 2 cos² ( p ) •

Перепишем уравнение (16) в виде

к

4У1 - x² - 1 + 2 x² 1 -x^

^f - 2 x    '

|

К 2^1 - x ² J^J

= 0 ^ 4 x ⁴ + 12 x²

—

= 0 о

15 = 0 •

Но   x ² =- ³ + V6,4T1 - x ² = 1 - 2 x ² = 4 - 2^6 < 0

и локальных точек экстремума нет x e (0,1) :

4 ( x , y ) = 1 + z 2 1 - 5 + 8( x + y ) — -( x ² + y ² — 1) I •     (17)

Исследуем на экстремум выражение, стоящее в круглых скобках формулы (17):

g ( x , y ) = - 5 + -( x + y )--( x + y - 1) ^ extr ^

g x ( x , y ) = 0 ° 8 ^{- 2} x = 0 ° x = ⁴ ,

g y ⁽ x , y ) = ⁰ °--- y = ⁰ ° y = ⁴ •

Но точка локального экстремума (4,4) £ [ - 1,1] х [ - 1,1] функции g ( x , y ). Из симметрии функционала также следует равенство координат в точке экстремума. Поэтому достаточно вычислить функцию g ( x , y ) в точках (-1, -1) и (1, 1).

g ( - 1, - 1) = - 5 + 8( - 1 - 1) - 1(1 + 1 - 1) = - 32 ,

g (1,1) = - 5 + -(1 + 1) - -(1 + 1 - 1) = 0 .

Для спектральной устойчивости достаточно, чтобы | 2 ( x , y )| <  1 V x , у е [ - 1,1] , то

1 - у z 2 = 1 + z 2 g ( - 1, - 1) = - 1 <  ^ ( x , У ) <  1 = 1 + z 2 g (1,1),

[1], [2] в системе (19). На границе прямоугольника в (19) значения функции вихря связаны с граничными значениями функции тока и компонентами скорости [1], [2].

П...к + 1        О.,,к + 1    _|_.,/-к + 1

к+1      /^  m,0 --Щ m,1 + Щ  m,2  Л

^; m ,0 =-------------------i-- 3--------

2 h2

w^{к + 1}

W    m , n ।

k +1         k +1         k +1            k +1

/ Щ    m , n,     О Щ     m , n ,-1 + Щ     m , n , -2  । ^ V m , n,

2h               h

m = 1, n ₂- 1

_w +1 _{0, n =}

_wk +1 _{n 2 , n}

32     ,         6

— z, = 2 О z, = —

3   ^{2          2}    32

3       Л 3

= 16, z ² '    ^0,16    .

Таким образом, если уравнение переноса спектрально устойчиво для любого закона: 2 у = const , то разностное уравнение (15) с h²

диффузионным членом спектрально устой-

Г„   3 1

чиво только на отрезке z ₂ е 0,— .

Или z ₂ = - ^ ^ < — о т <  —Re h ² (*)•

²    Re h²    16      ⁰    16

В формуле (*) шаг т ₀ максимальный (соответствует верхней границе спектральной устойчивости) в задаче (1). На практике реальный шаг времени разностной схемы т 1 = т ₀ / n много меньше т ₀ из-за решения других уравнений системы в (1) и 2 особых точек поля скорости.

Обозначим реальный шаг

Т     3

т = —, п т < — Re h ² = т .

¹ п ¹   16            ⁰

Видно, что при достаточно большой кратности расщепления n явной разностной схемы (4) с шагом Т 1 всегда можно выполнить 3_ условие п т <  — Re h ² .

Отметим, что поиск новых значений вихря в цикле (4) проводится только для внутренних узлов, то есть для узлов первого прямоугольного контура и узлов, расположенных дальше от границы прямоугольника.

Граничные значения вихря со вторым порядком погрешности приведены в работах

7/ ^{+ 1}0, n - 8/ ^{+ 1}1, n + / ^{+ 1}2, n   ₃ u ^{k + 1}0, n

2 h ₂ ²                      h ₂

k +1              k +1               k +1                  k +1

/ Щ    n 2 , n - - Щ n 2 -1, n + Щ     n 2 -2, n uU   n 2 , n

---------------------i--3---------

2 h₂²                      h

n = 1, n - 1,

к +1     । i + +1

к +1        w 0,1 ⁺ w 1,0     к +1

W 0,0 =---------------- , W i

,2

.к +1           । ,.,k +1

к +1         ^w   0, n 1 -1 + w 1, n 1

. w °^Л=         2

ⁿ 2 , ⁿ l

W^{k + 1} n ₂, n 1 -1 + W^{k + 1} n ₂

W к +1

> ^W n 2,0 =

w ^{1 + 1} n ₂,1 + w ¹

-1, n ₁

, (19)

, к +1

’ n 2 -1,0

.

Оценим время решения задачи (1) в трех случаях.

В первом случае (алгоритм А) система уравнений (1) решается последовательно, алгоритм расщепления ( n = 1) в системе уравнений (4) не используется, временной шаг ( т 1 = т о / n = т о ).

Во втором случае (алгоритм В) уравнение вихря (4) решается на двухслойной схеме с кратностью расщепления n =100. В алгоритме С n = 200 и трехслойная схема по времени. Программы алгоритмов А, В, С запускались одновременно и заметного временного различия для достижения выбранного числа итераций (внешней переменной цикла к) не обнаружено (из-за простоты явной разностной схемы (4)). Но если для наступления стационарного режима в алгоритме В было достаточно 1,5 часа работы программы, то для алгоритма А стационарный режим не был достигнут после двух суток работы программы. Тогда ( т а / т в ) ~ (3/16)/(1/300) = 56 (рис. 2).

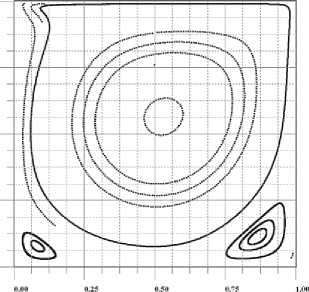
На рис. 1 показано поле линий тока для решения задачи с кратностью n =1 (отсутствие расщепления). Видно, что спустя 6000 шагов времени поле линий тока находится далеко от стационарного состояния. Центральный вихрь первого порядка обменивается моментом импульса с вихрями второго порядка, расположенных в нижних правом и левом углах прямоугольной каверны.

В работе [3] авторы А.А. Фомин и Л.Н. Фомина также получили численно стационарное решение задачи (1) и вихри трех порядков.

В работе Фоминых большее разрешение сетки 2500×2500 (Re>10000), число ячеек в нашей сетке 100×100 (и Re=1000 – в 10 раз меньше). Хотя нестационарный вихрь третьего порядка обнаружен нами на рис. 1.

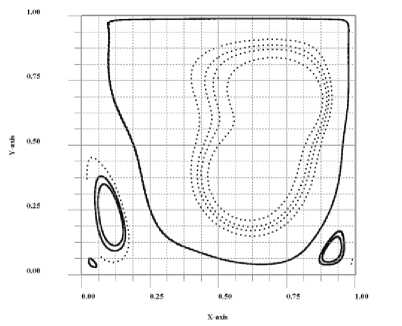
Рис. 1. Поле линий тока для решения задачи (1) без расщепления (n=1) Re=1000.

h ² Re

Шаг времени    т =      , п = п2 = 100, h = 1/100 в момент t = 6000 т

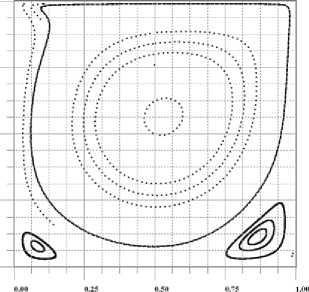
На рис. 2 показаны поля линий тока в предельных стационарных состояниях.

Рис. 2(А) соответствует решению задачи (1) без расщепления.

Рис. 2(В) соответствует решению задачи (4) с расщеплением n=100 с двухслойной аппроксимацией производной по времени к+ k+(i+1)/п ^к+i / п и первым порядком погреш-

Т 0/ п ности O (т1), стационарное состояние достига-

A

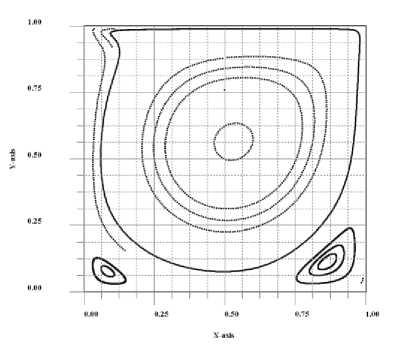
ется спустя N=21000 итераций, после чего max и min значения функции тока сохраняются с 15 значащими цифрами.

Третий рисунок (рис. 2(С)) соответ- ствует стационарному решению с трехслойной k+(i+1)/n       k+(i—i)/n w    — w временной производной                 и

2т 0/ n со вторым порядком погрешности O(т2) и с кратностью расщепления n=200.

Поле тока становится стационарным спустя N=43000 итераций.

C

Рис. 2. Установившееся поле линий тока для задачи (1), число Рейнольдса Re=1000, n - кратность расщепления, т 1 = т ₀/ п.

h ² Re

Рис. 2(A). т = т =       , t = 400000 т , п = 1 ;

1    0     ₃₀₀

Рис. 2(B). т = —h 2 Re, t = 21000 т ₀, п = 100 ;

Рис. 2(C). т = h ² Re , t = 43000 т , п = 200 16                    ⁰

Общими показателями решения (1) являются максимальное и минимальное значение поля функции тока, поскольку все остальные поля можно получить через дифференциальные операторы от поля функции тока (как видно из задачи (1)).

Рассмотрим max и min значения функции тока в предельном (стационарном) состоянии решения задачи (1) для трех случаев:

Таблица 1. Сравнение значащих цифр в стационарном поле функции тока в задаче (1) для различных алгоритмов

Алгоритм	V max	V min
A) n=1	1,71588 10-3	-0,1183079
B) n=100	1,715838733007 10-3	-0,1183038468
C) n=200	1,715838733009 10-3	-0,1183038468

Примечание:

А)n=1 (2-х слойная схема), N=400000; B)n=100 (2-х слойная схема), N=21000; C)n=200 (3-слойная схема), N=43000

Таблица 2. Сравнение значащих цифр в нескольких точках стационарного поля горизонтальной компоненты скорости в задаче (1) для трех алгоритмов

Ал-горит м	A:n=1	B:n=100	C:n=200
r 1	3,25838 9 10-2	3,258397414826 9 10-2	3,258397414825 7 10-2
r 2	-9,772 15 10-2	-9,77226561 55239 10-2	-9,77226561 55180 10-2
r 3	-1,732 42 10-2	-1,73241760 2921899 10-2	-1,73241760 2922225 10-2

Анализ ψ min , ψ max показывает, что два разных алгоритма: B – двухслойная схема по времени с расщеплением n =100; C – трехслойная временная схема с n =200 дают одинаковые предельные решения, в которых стационарные ψ min , ψ max совпадают в 11–12 значащих цифрах (табл. 1). То же можно сказать о горизонтальной компоненте u стационарного поля скорости в нескольких, но одних и тех же узлах сетки – совпадение в 11–12 значащих цифрах (табл. 2). Поэтому рис. 2(B) и рис. 2(C) неразличимы графически.

Решение без расщепления (алгоритм A) и решения с расщеплением (алгоритмы B, C) совпадают в 5 значащих цифрах.

Основные полученные результаты:

• 1)    Впервые предложен алгоритм (4) n-кратного расщепления ( n =100, 200), явной разностной схемы для уравнения вихря в десятки раз ускоряющий время решения гидродинамической задачи.

• 2)    В предельных случаях с большими и малыми числами Рейнольдса показано, что для спектральной устойчивости разностной схемы уравнения вихря следует выбирать закон [5], [6] стремления к нулю τ 0 , h .

T = O ( h ² ), т , h ^ 0, п т - ~ h 2 Re = T •

0              0               1     ₁₆              0

• 3)    Решения с расщеплением в системе

уравнений (1) и шагом времени т0 = — h Re соответствуют     верхней     границе спектральной устойчивости. Спектральная устойчивость с г0 подтверждена численно.

• 4)    Предложена двухслойная временная схема для уравнения вихря с аппроксимацией O (г + h ⁴).